无标度网络上带有隔离项的时滞SIQRS模型稳定性分析

徐云程，胡 华宁夏大学数学统计学院，宁夏银川750021

0 引言

随着复杂网络这门新兴学科的迅速兴起及无标度网络的提出［1］，人们发现生活中大量的复杂系统均表现出无标度性（度分布为P(k)=Ck-γ(2＜γ≤3)），如万维网、交通网、接触网等［2，3］。于是利用复杂网络研究传染病的动力学行为引起了许多学者的广泛关注［4～7］，其中最为经典的是文献［6］，它在研究无标度网络上的SIS模型时发现：当网络规模趋于无穷大时，传播阈值趋于零，这很好地解释了计算机病毒长期存在而不能绝迹的原因。隔离措施在控制传染病的传播中发挥着举足轻重的作用，为探究隔离措施对控制疾病传播的影响，文献［7］提出了复杂网络上带有隔离项及疫苗接种的SIQRS传染病模型

其中，Sk(t)，Ik(t)，Qk(t)，Rk(t)分别表示t时刻度为k(=1，2，…，n)的易感者、感染者、隔离者、恢复者的密度，Θ(t)=表示任意一条给定的边与一个染病者相连的概率，k(=1，2，…，n)表示节点的度（即一个人在单位时间内接触的人数），β表示传播率系数，α是易感者的疫苗接种率，δ是恢复者的失去免疫率，σ是感染者的隔离率，γ是感染者的治愈率，ε是隔离者的治愈率。

事实上，许多传染病在传播过程均表现出时滞性，主要有潜伏期时滞、免疫期时滞、感染期时滞［8，9］等。文献［10］分析了时滞、非线性发病率等因素对无标度网络上的SIS模型动力学行为的影响。文献［11］研究了无标度网络上具有时滞的SEIRS传染病模型，表明时滞对基本再生数无影响。文献［12］通过选取时滞作为分支参数，得到了具有非线性发病率的时滞SEIS模型Hopf分支存在的条件。文献［13］研究了预警意识、延迟提供预警资金对经典SEIR模型动力学行为的影响。这些研究在建立模型时均假设时滞为单值，然而许多病原体的感染期和潜伏期等会随着环境的变化而发生变化，不同的感染者由于自身健康状况的差异性，恢复期也会有所不同，为更好地揭示这种时滞现象，文献［14］通过将t时刻的发病率假设为提出了复杂网络上具有分布时滞的SIR模型，其中表示感染个体在潜伏期的存活概率，可积函数f(τ)用来描述感染性随时间变化的情况，满足f(τ)≥0，τ∈[0，∞)且

由于复杂网络上的传染病模型维数较高，分析其动力学行为较为困难，所以文献［7］未讨论地方病平衡态的稳定性；文献［14］所构建的SIR模型未考虑疫苗注射、隔离措施等因素的影响，所以模型耦合度较低，故作者将模型解耦后利用基尔霍夫矩阵树定理分析了模型的全局动力学行为。本文综合考虑了文献［7］中的隔离措施、疫苗注射及文献［14］中的时滞因素，提出了无标度网络上带有隔离项的时滞SIQRS模型

1 平衡态的存在性

显然，模型（2）的初值满足

定理1令(S1(t)，I1(t)，Q1(t)，R1(t)…，Sn(t)，In(t)，Qn(t)，Rn(t))为模型（2）满足初值条件（3）的解，则当t＞0时，有0＜Sk(t)，Ik(t)，Qk(t)，Rk(t)＜1(k=1，2，…，n)且0＜Θ(t)＜1。

证首先证明当t＞0时，有Ik(t)＜1(k=1，2，…，n)。因为Ik(t)连续，所以存在一个ξ＞0，使得当t∈(0，ξ)有Ik(t)＜1。假设当t＞0时，Ik(t)=1(k=1，2，…，n)，则存在一个t0≥ξ＞0，使得Ik(t0)=1，且当t∈(0，t0)有Ik(t)＜1。

接着证明当t＞0时，有Ik(t)＞0(k=1，2，…，n)。对模型（2）的第二个式子两边从0到t积分可得

假设当t＞0时，有Ik(t)=0(k=1，2，…，n)，则存在一个t1＞0，使得Ik(t1)=0。而由（4）式可知

与假设矛盾，所以当t＞0时，有Ik(t)＞0(k=1，2，…，n)。

综上可得，当t＞0时，有0＜Ik(t)＜1(k=1，2，…，n)。

显然，当t＞0时，有0＜Θ(t)＜1。同理可证，当t＞0时，有0＜，Qk(t)，Rk(t)＜1(k=1,2,…,n)。

使用归一化条件，有

将（5）式代入Θ得

2 平衡态的全局稳定性

2.1 无病平衡态的稳定性

为书写方便，这里将“～”省略。接着探究线性模型（8）的稳定性，不妨假设其有如下形式的指数解

其中Sk0，Ik0，Qk0，Rk0(k=1，2，…，n)表示模型（8）的初值，将（9）式代入模型（8）得

其中，ρ为模型（8）的特征值。令

通过计算得：矩阵A有n重特征值-μ，n重特征值-(μ+δ+α)及n重特征值-(μ+ε)，为得到矩阵A的其余特征值，定义

通过相似变换，可得矩阵Λ的相似矩阵

显然，矩阵Λ*有n-1重特征值-(σ+γ+μ)及特征值

假设η=a+bi，则有

分离实部和虚部得

接着，考虑无病平衡态的全局稳定性。

接着，构造一个满足Mk(0)=Ik(0)≥0的等价系统如下

由比较原则得

令ε2→0有

2.2 地方病平衡态的稳定性

定理5定义

定义李雅普诺夫函数

定的。对任意给定的ε＞0，定义

注1由

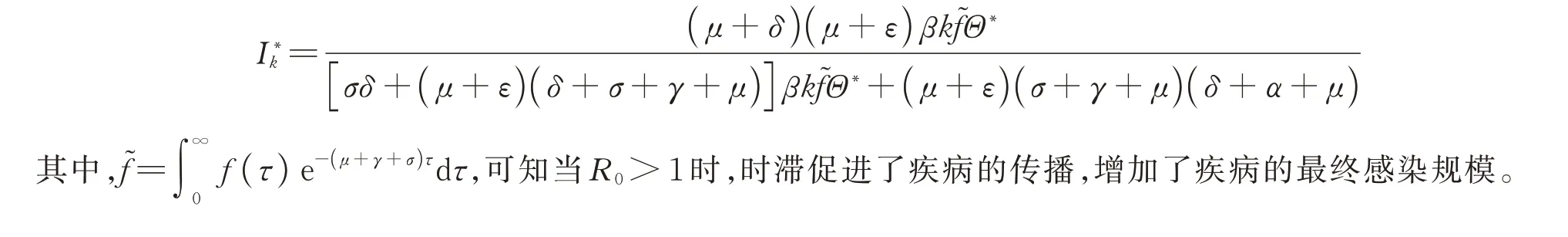
3 数值模拟

首先，利用BA算法［1］生成一个含有800个节点的无标度网络Q，生成参数为m0=5，m=1，下面的数值模拟基于网络Q进行。

例1选取参数μ=0.5，δ=0.7，σ=0.8，γ=0.5，α=0.9，β=0.6，ε=0.9，f(τ)=0.5e-0.5τ，0≤τ≤∞，得R0=易感者、感染者、隔离者、恢复者随时间变化的轨迹如图1。从图1可以看出无病平衡态全局渐近稳定，这说明了定理3的有效性。当τ分别取3、4、5，感染者的密度随时间的变化轨迹如图2，疾病最终消失。

图1 R0＜1时的时间序列图Fig.1 The time series with R0＜1

图2 R0＜1时具有不同τ的时间序列图Fig.2 The time series with differentτwhen R0＜1

例2选取参β=0.6，μ=0.05，δ=0.08，σ=0.06，γ=0.15，α=0.1，ε=0.1，f(τ)=0.5e-0.5τ，0≤τ≤易感者、感染者、隔离者、恢复者随时间变化的轨迹如图3。从图3可看出地方病平衡态全局渐近稳定，这说明了定理4的有效性。当τ分别取3、4、5，感染者的密度随时间的变化轨迹如图4，疾病永久存在。∞，得

图3 R0＞1时的时间序列图Fig.3 The time series with R0＞1

图4 R0＞1时具有不同τ的时间序列图Fig.4 The time series with differentτwhen R0＞1

4 结语

本文综合考虑了接触异质性、隔离措施、疫苗注射、时滞等因素，建立了更加符合实际的无标度网络上带有隔离项的时滞SIQRS模型。分析了网络的拓扑结构、时滞、隔离措施等因素对基本再生数R0大小的影响，发现基本再生数R0与网络的异质性呈正相关、与隔离率σ呈负相关、与疾病的感染性f(τ)呈正相关。通过构造合适的李雅普诺夫函数证明了平衡态的全局稳定性，结果表明：当R0≤1时，无病平衡态全局渐近稳定，即疾病最终消失；否则地方病平衡态全局渐近稳定，即疾病永久存在。利用MATLAB软件对分析结果进行了数值模拟，发现当R0＜1时，时滞减缓了疾病的传播；当R0＞1时，时滞促进了疾病的传播。

虽然隔离措施可以降低基本再生数，但由于隔离措施会对经济发展产生消极的影响，且当基本再生数R0≤1时，隔离措施无法起到控制疾病传播的作用，只有当基本再生数R0＞1时，隔离措施可以在一定程度控制疾病的传播。因此，选择恰当的时机实施隔离措施既能有效地控制疾病的传播，也不会对经济发展产生太大的影响。

由于本文所建模型耦合度较高，所以如何构造合适的李雅普诺夫函数来分析其动力学行为有一定的挑战性，故本文利用归一化条件和线性变换将模型进行降维及线性化处理。其次，由于复杂网络上的传染病模型维度较高，因此如何从理论上给出复杂网络上的时滞传染病模型Hopf分支存在的条件是一个值得研究的课题。事实上，由于生物系统中环境的变化，疾病在传播过程中或多或少都会受到随机噪声的影响，所以将随机干扰引入到模型中是随后的一个研究方向。