含混合高斯项的AR-GJR-GARCH模型的贝叶斯估计

王祥赛

武汉大学数学与统计学院，湖北武汉430072

0 引言

在对市场的风险研究中，波动率作为其中重要的一个度量，一直被认为是风险管理等方面的一个重点研究对象。在波动率研究方面，Engle［1］提出了ARCH（autoregressive conditional heteroscedasticity）模型，Bollerslev［2］在其研究的基础上又提出了GARCH（generalized ARCH）模型，该模型一定程度上包含了ARCH模型所不能涵盖的市场信息。但随着研究的深入，很多学者发现，现存的模型对一些金融数据的集聚性、尖峰厚尾性等不能做出解释。为解释这些特性，Nelson［3］提出了EARCH（exponential ARCH）模型，Glosten等［4］提出了GJR（Glosten-Jagannanthan-Runkle）-GARCH模型。

AR（autoregressive）-GJR-GARCH模型是在GJR-GARCH模型的基础上，进一步添加了自回归项发展而来，对此类模型的参数估计通常是采用贝叶斯估计法［5］。但在贝叶斯估计的后验分布中通常存在一个未知的数值积分项，这使得直接获取后验分布的解析形式比较困难。为解决这个问题，Alexander等［6］用Griddy-Gibbs方法对后验分布进行抽样，但是这种方法在每次迭代前均需对数值积分做一个估计，导致计算成本比较高。

Chen等［7］和Talay［8］在引入物理学中哈密尔顿系统的基础上，提出了一种随机梯度哈密尔顿蒙特卡洛（stochastic gradient Hamiltonian Monte Carlo，SGHMC）方法，该方法在未知数值积分项时，也可以获取一系列服从目标后验分布的样本，而且不需要引入M-H（Metropolis-Hasting）步骤，因而该方法的计算复杂度大大降低。基于此方法，Kim等［9］在贝叶斯神经网络的应用上取得了进展。

本文在张新星等［10］给出的含混合高斯项的AR-GJR-GARCH模型基础上，采用SGHMC方法对后验分布进行采样，给出了最终的参数估计结果，并结合结果对原始数据所包含的信息进行了解释。

1 含混合高斯项的AR-GJR-GARCH模型及贝叶斯后验密度

AR（s）-GJR-GARCH（p，q）模型如下（其中，s，p，q表示相应的滞后阶数）

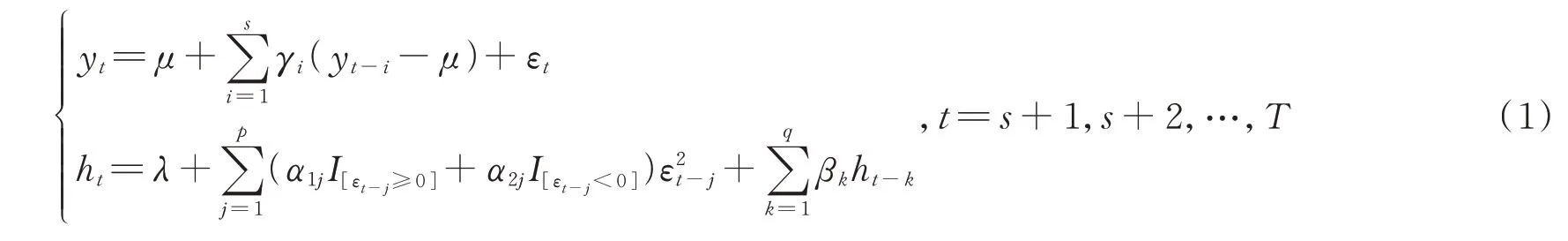
其中，yt为观察样本，μ为观察变量的长期稳定均值，T为观察样本总数，I为示性函数，r=max{s，p，q}。实际情况中，为了确保AR（s）过程的平稳性，滞后算子B的多项式的零点在单位圆外。

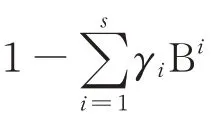
εt为一混合高斯分布项，即

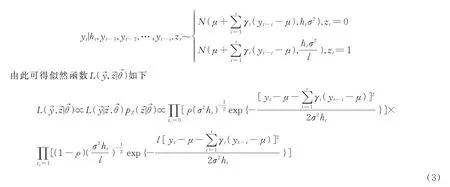
各参数的先验分布按照下面形式选取

2 随机梯度哈密尔顿蒙特卡洛法

随机梯度哈密尔顿蒙特卡洛法是在哈密尔顿系统的基础上发展而来。假定观察样本的集合为Ω，我们感兴趣的参数θ，其基于样本观察值x∈Ω的后验密度p(θ|Ω)形式如下

这里将U(θ)称为势能函数，根据贝叶斯定理，该函数有如下形式

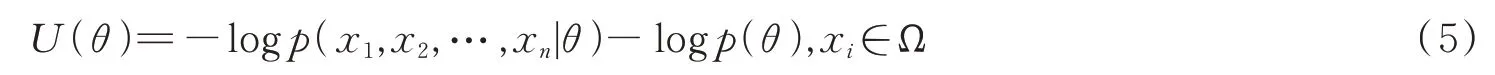
其中，p(x1，x2，…，xn|θ)为在给定θ时样本的条件概率密度，p(θ)为θ的先验概率密度。

为了使用哈密尔顿系统，还需要一个关于动能的函数，这里记动量变量为r，r一般为人为设置的辅助变量且服从正态分布N(0，M)，M称之为质量矩阵且一般为单位矩阵I。由θ和r一起构造如下形式的微分方程组

其中，∇U(θ)为U(θ)的梯度，这样的微分方程组形成的系统称为哈密尔顿系统。去掉采集到的样本r那一部分，剩下的θ那一部分即为我们需要的满足后验分布p(θ|Ω)的样本。

而随机梯度汉密尔顿蒙特卡洛法是对原有使用的∇U(θ)进行调整，不再选用全部的样本集计算，而是从Ω中随机抽取一个子集出来，并定义如下形式的随机梯度

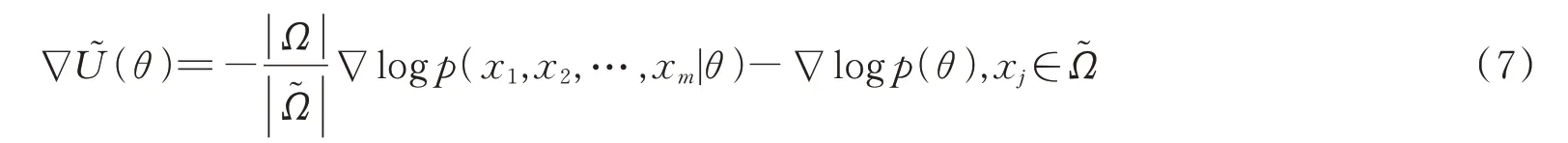
由中心极限定理可知

但该形式并不能保证对应的哈密尔顿系统收敛到我们想要的平稳分布π(θ，r)，需要添加一项进行修正，因此得到如下形式的微分方程组

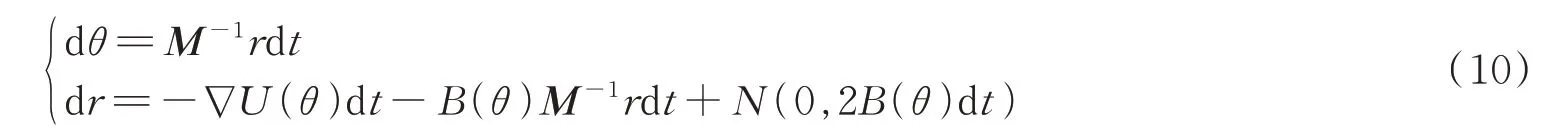
为方便讨论，这里假定B(θ)和θ无关，将其简记为B。下面给出证明，该方程组可以收敛到我们想要的平稳分布π(θ，r)。

定理1微分方程组

由Fokker-Planck方程易知，在t时刻(θ，r)的联合概率密度pt(θ，r)有如下等式

在实际应用中，通常不知道B的具体形式，因此要先利用样本对B做一个估计，记为然后人为指定一项C≥，从而（11）式的第二个微分方程变为如下形式

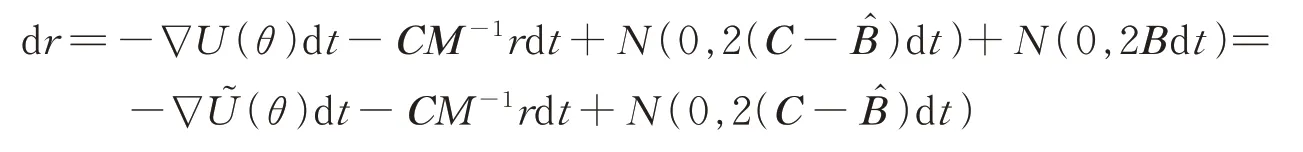
为了能尽可能多地利用观察样本的信息，在每构建一个哈密尔顿系统前随机抽取一个样本子集进行随机梯度的计算，这样就克服了仅使用单一样本子集信息量不足的缺陷，具体算法如下：

步骤1给定初值要采集的样本数n，内循环次数m，步长δ，矩阵C和

3 实例分析

在实例分析中采用中证医药2019年3月13日—2020年11月3日的指数收盘价数据的变化率，数据集总计有398个数据，将其拆分为2019年3月13日—2020年1月2日199个数据以及2020年1月3日—2020年11月3日199个数据分别利用上述模型进行分析。这两部分的数据集的时间序列分别如图1和图2。

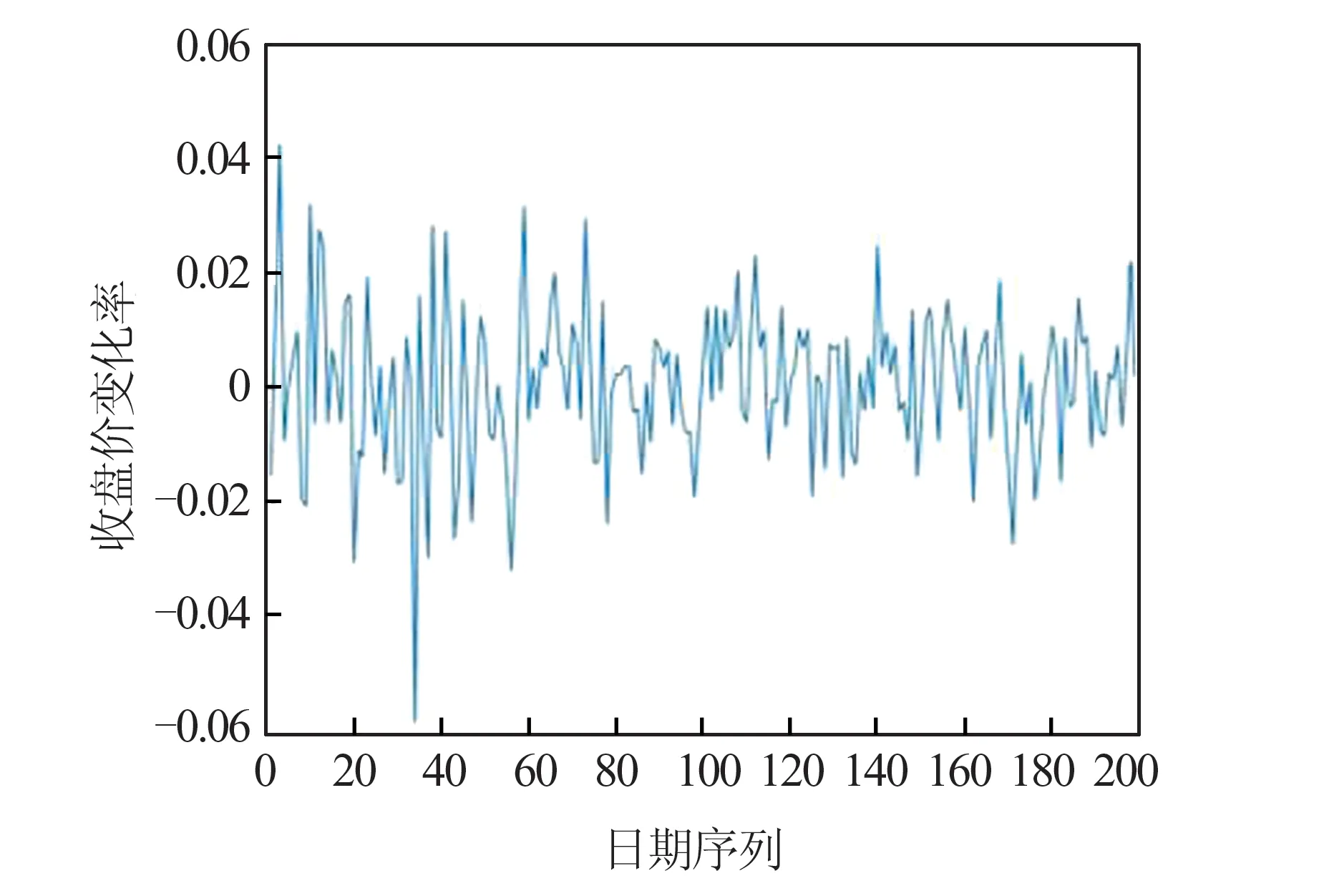
图1 2019.3.13—2020.1.2收盘价变化率时间序列Fig.1 Time series of closing price change rate from March 13,2019 to January 2,2020

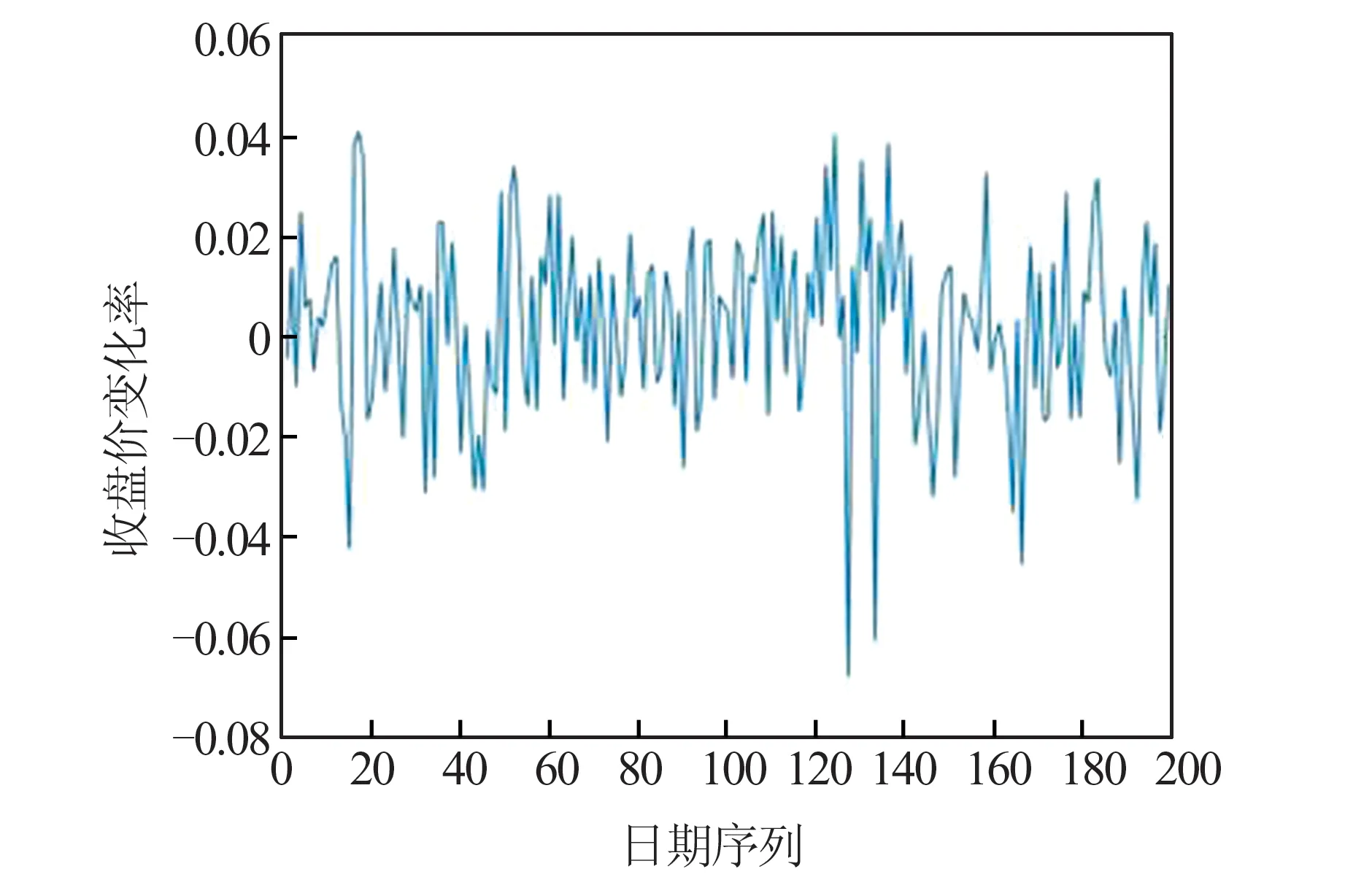
图2 2020.1.3—2020.11.3收盘价变化率时间序列Fig.2 Time series of closing price change rate from January 3,2020 to November 3,2020

从图1和图2中可以发现这两部分数据的波动幅度随时间变化，因此适合用异方差模型进行估计，进一步绘制了两组数据的偏自相关函数（autocorrelation function，ACF）图，如图3和图4。

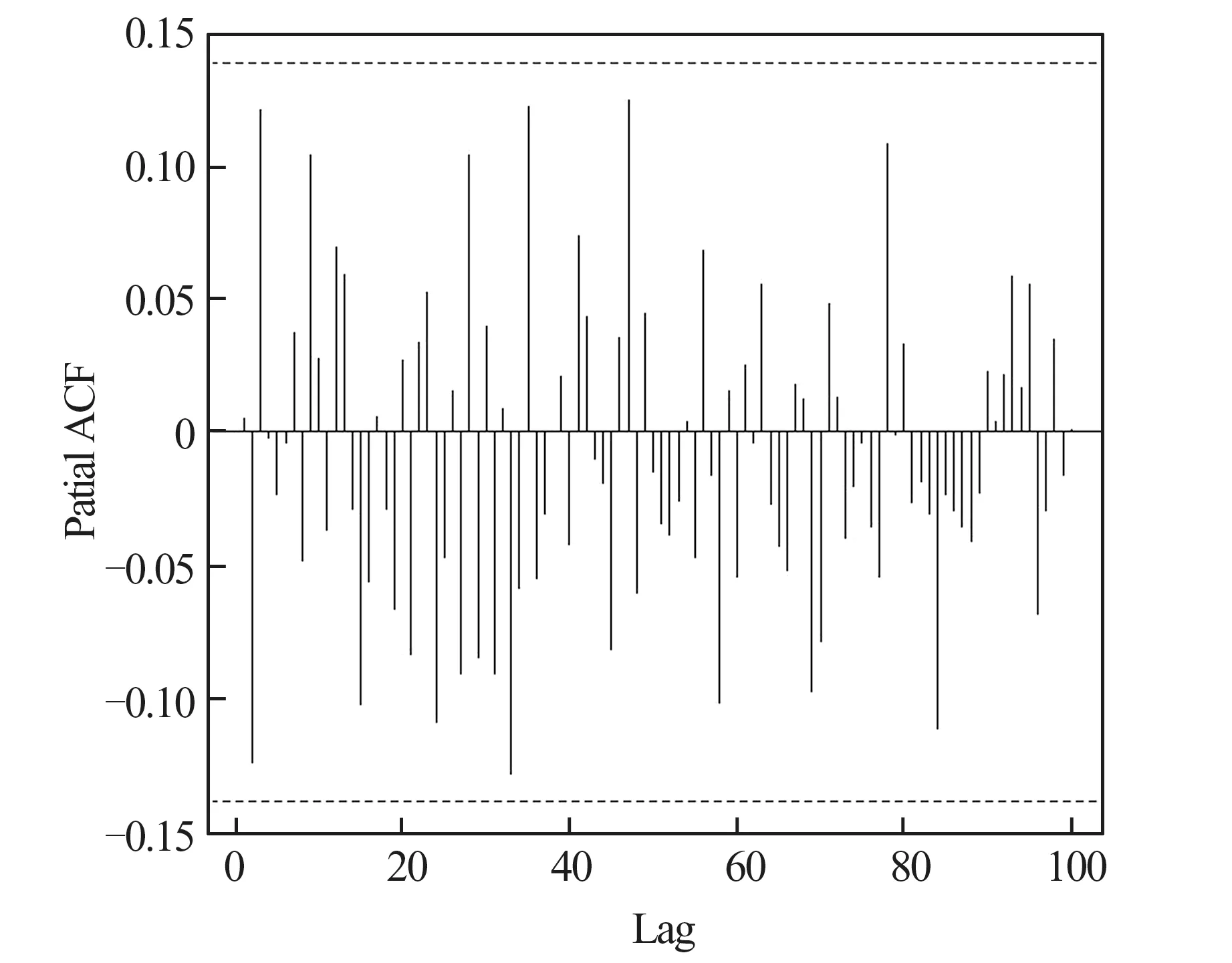
图3 2019.3.13—2020.1.2收盘价变化率偏自相关函数Fig.3 Close price change rate partial autocorrelation function from March 13,2019 to January 2,2020

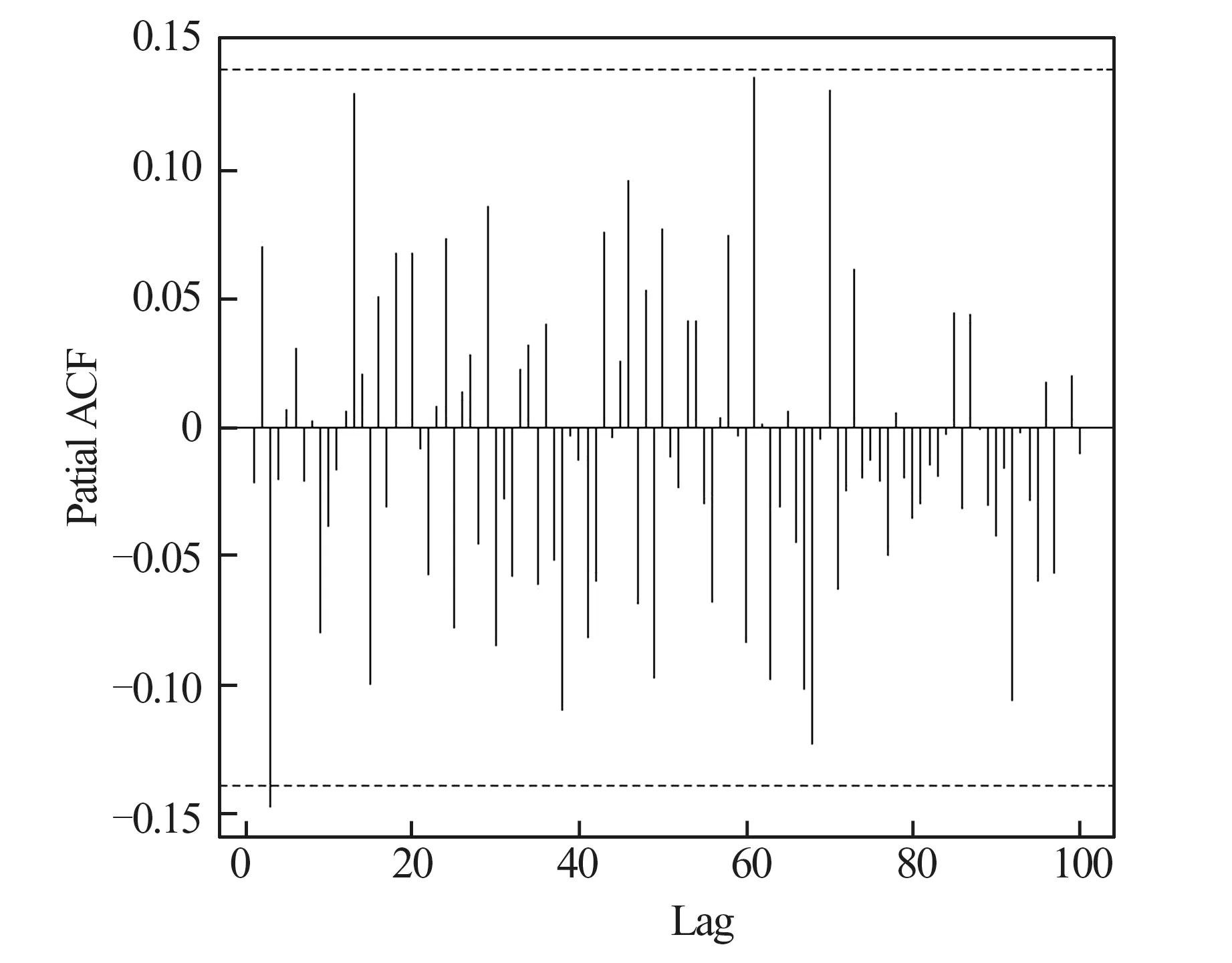
图4 2020.1.3—2020.11.3收盘价变化率偏自相关函数Fig.4 Close price change rate partial autocorrelation function from January 3,2020 to November 3,2020

可以发现两组数据的偏自相关函数都是1阶截尾的，因此选用AR（1）-GJR-GARCH（1，1）模型比较合适。利用MATLAB软件使用SGHMC算法来对该模型的参数进行贝叶斯估计，每次内循环开始前从数据集中随机选择99个数据作为子集，并设置y1=0。利用该算法获取1 000个样本，分别得到这两组数据的参数估计结果如表1和表2。

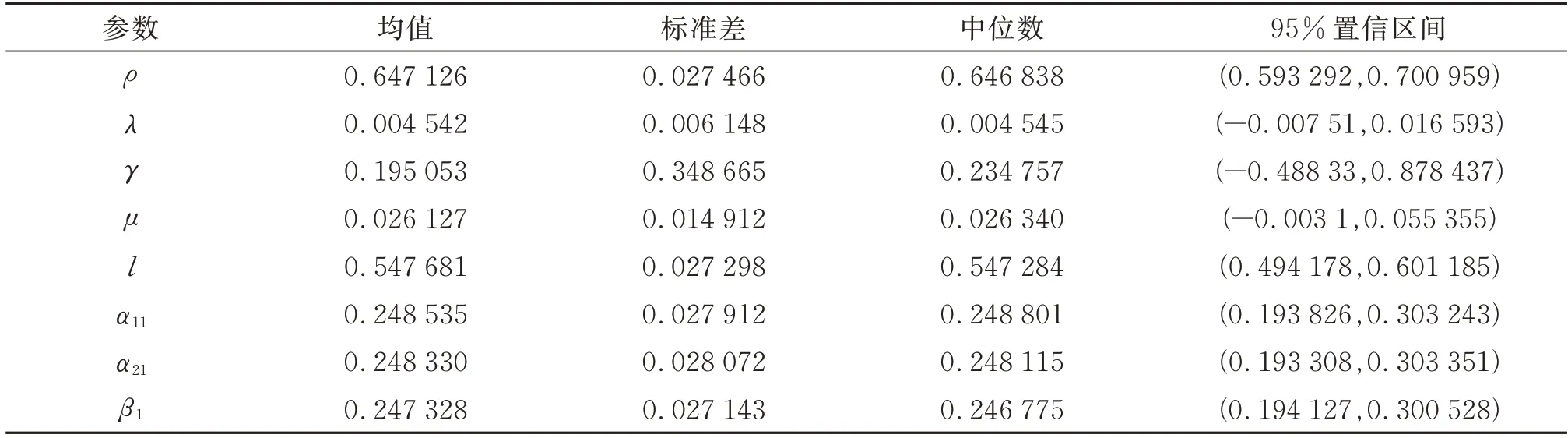
表1 2019.3.13—2020.1.2参数估计结果表Table1 Parameter estimation result from March 13,2019 to January 2,2020

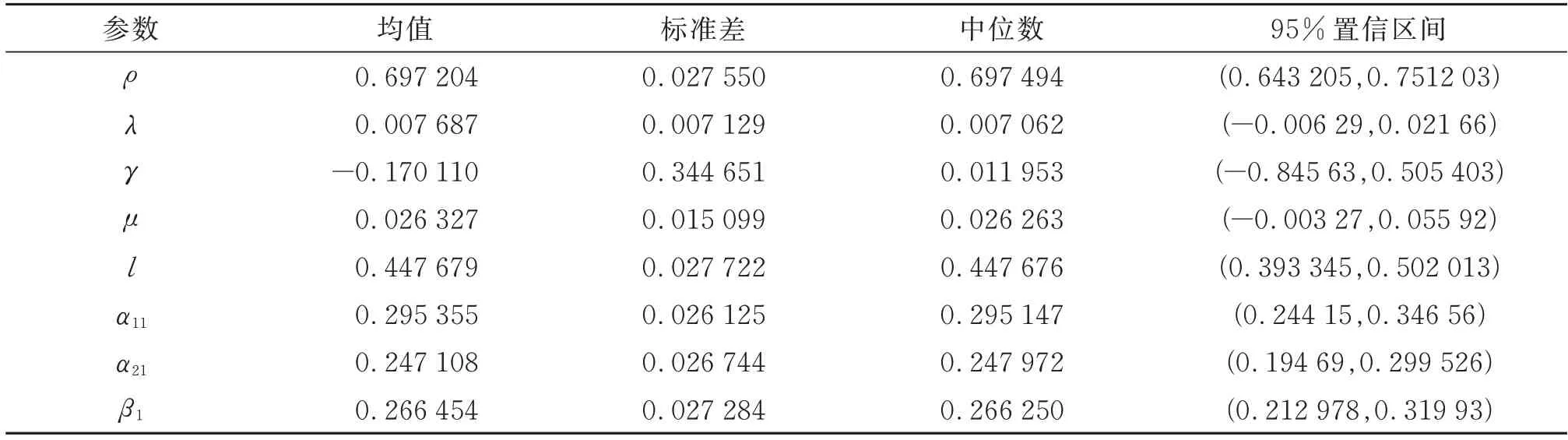
表2 2020.1.3—2020.11.3参数估计结果表Table2 Parameter estimation result from January 3,2020 to November 3,2020

综上，我们的模型一定程度上反映了该指数在一段时期内的背景信息，利用该模型可以对市场信息作一定的解释。

4 结语

本文利用随机梯度哈密尔顿蒙特卡洛方法在后验密度解析形式未知的情况下得到了含混合高斯项的AR-GJR-GARCH模型各参数的贝叶斯估计。该方法相比于前人的Griddy-Gibbs方法优势在于无需在每次迭代前再对一个复杂积分项进行数值估计，降低了计算复杂度。实例分析给出了AR（1）-GJR-GARCH（1，1）模型在中证医药2019年3月13日—2020年11月3日指数收盘价数据变化率下的参数贝叶斯估计值，并根据得到的估计值推算市场背后信息，发现其较好地反映了该指数的市场波动情况与好坏消息对该指数的影响，验证了模型和方法的合理性。