考虑绿色度的双渠道农产品供应链决策协调研究

陈 琪，姚慧丽，李晓萍

(江苏科技大学 经济管理学院，镇江 212100)

网络时代的到来，一些制造商开始从线下零售单渠道运营模式转向线下和线上相结合的双渠道运营模式.研究表明，双渠道供应链的引入，使企业提高了市场占有率，增加了企业的利润.目前，国内外不少学者对绿色供应链进行研究，并取得一定的成果.文献[1-2]通过分析影响绿色生鲜农产品网购意愿的因素，发现绿色生鲜农产品的质量、安全、新鲜度与网购意愿呈正相关，只有新鲜、绿色的农产品，才更有可能赢得市场.多数消费者从绿色偏好[3-4]、环保意识[5]以及低碳角度[6]来研究.文献[7]将消费者绿色偏好反应到产品估价中，讨论绿色供应链中生产企业的产品价格最优决策问题.文献[8]从横向竞争角度入手，分析制造商横向竞争与合作情形下的4种博弈模型，得出制造商竞争与合作能够对双方利润、产品价格及零售商利润造成影响.另外，制造商双渠道的运营模式也是非常重要的[9].目前只有较少学者进行农产品双渠道运营模式的研究.文献[10]从价格和服务竞争角度，以收益共享契约模型为基础，通过建立以制造商领头模型，实现闭环双渠道供应链的帕累托优化.文献[11]引入两级物流服务商，研究交叉服务水平对决策的影响，得出随着交叉服务水平敏感性系数的增加，FLSP(指多功能物流服务提供商)的利润先增加后减少.文献[12]考虑消费者可追溯性意识的三级双渠道供应链，对是否运用区块链技术研究最优定价策略.结果表明，技术的运用与消费者的可追溯性意识、供应商和制造商的生产成本以及使用区块链技术的成本有关.文献[13]主要研究零售商在线上和线下两个渠道销售短周期产品时，要制定合适的价格策略来避免两个渠道的冲突.文献[14]主要研究在集成系统和Stackeberg博弈下，得出二级双渠道供应链的最优价格决策.文献[15]提出分层定价法，并且分析单一渠道双渠道的绩效受价格策略影响的程度和表现.

通过对文献的梳理，学者们对供应链的研究已相当充分，但多是研究单渠道供应链或绿色供应链，但很少有将绿色供应链、双渠道供应链以及农产品供应链结合起来研究.文中将三者结合，通过对不同决策考虑绿色度的双渠道农产品供应链博弈分析，并用数值分析进一步验证，最后制定二部契约，对供应链成员之间的合作进行讨论.

1 问题描述与研究假设

1.1 问题描述

随着农产品的发展以及当前环境的严重性，说明实施绿色供应链的重要性，主要考虑农产品绿色程度并将其量化，对流通绿色农产品双渠道供应链在不同模型中农产品绿色度、销售价格、需求量以及利润进行求解及分析.并对农产品绿色度对价格、及利润的影响，以及渠道市场份额、投入成本、两渠道销量敏感系数对制造商和零售商参与绿色供应链意愿的影响等进行探讨.

表1 变量说明

1.2 符号说明

1.3 模型相关假设

考虑分析的简便性，现做以下假设：

(1) 制造商和零售商均为理性人，均先考虑自身利益的最大化.

(2) 制造商和零售商的需求量即为销量.

(3) 线下零售和线上直销的绿色农产品是无差异的，并且两者的销售价格是一样的，其中：销售价格是零售商制定，批发价格是制造商制定.

(4) 根据微观经济学理论，将需求的价格弹性系数为b，并且呈线性关系.

(5) 随着物流配送服务水平的提高，线上销售数量增加，线下销售数量减少，物流配送对线上、线下需求量影响分别为um、ur，且um>ur，物流成本Cz与物流服务水平z为二次方关系：Cz=X+βz2.

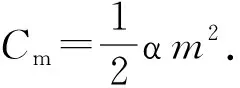
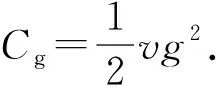
要使模型成立，则需要线下零售量、线上直销量以及制造商和零售商的利润为正，即需满足：

由以上假设可知，在双渠道供应链中，线下零售渠道和线上直销渠道的销量分别为：

Dr=Qs-bp-urz+σrg+rrm

(1)

Dm=Q(1-s)-bp+umz+σmg+rmm

(2)

2 最优决策模型构建与分析

2.1 分散决策博弈模型

农产品的绿色度和批发价格是制造商决定的，而零售商则根据制造商的决定来决定销售价格以实现自身利益的最大化.在分散决策模型中，零售商的利润函数为：

(p-w)(Qs-bp-urz+σrg+rrm)-

(3)

(4)

在分散决策模式下，作为领导者的制造商的利润函数为：

(p-c)(Q(1-s)-bp+umz+σmg+

rmm)+(w-c)(Qs-bp-urz+σrg+

(5)

将式(4)代入式(5)，可得制造商关于农产品绿色度、批发价格的利润函数，并对绿色度和批发价格求偏导得：

(6)

(7)

(8)

(9)

其中:

(10)

(11)

(12)

分散决策模式下，双渠道供应链上的总的销售量为：

(13)

将式(8～12)带入式(3、5)中，可得线下零售商和制造商的利润分别为：

(14)

(15)

双渠道供应链上整体最大利润为：

(16)

2.2 集中决策博弈模型

集中决策时，双渠道供应链总利润函数表达式为：

(17)

由式(17)分别对销售价格以及绿色度求偏导得：

4bp+(σr+σm)g

(18)

(19)

由于供应链总利润海塞矩阵一阶主子式-4b<0，当二阶主子式4bv-(σr+σm)2>0时，海塞矩阵为负定，利润函数是p、g的凹函数，所以存在p、g最优解，使得利润达到最大值.

(20)

(21)

将式(20、21)代入式(1、2)，可得集中决策模式下线下渠道和线上渠道的销量分别为：

(22)

(23)

集中决策模式下，双渠道供应链农产品的总销量为：

(24)

将式(20～23)代入集中决策模式利润函数式(17)中，得：

(25)

2.3 分散决策和集中决策模型比较分析

通过对比分散决策模式和集中决策模式下农产品最优绿色度、最优两渠道销量以及最优供应链的总利润，可得命题：

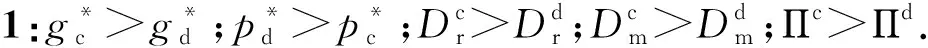
证明过程见附录.由命题1可知，在集中决策模式下，农产品绿色度更高，销售价格更低，两渠道销售数量更多，总利润更大.在分散决策模式下，零售商主要是通过提高价格获得更高利润，而制造商主要是通过提高批发价格获得更高利润.然而对于消费者而言，面对更高的价格而不能得到绿色度更高的农产品，因此会降低消费者购买的欲望，最终导致整条供应链上的总利润降低.

命题2表明：在分散模式下，随着线下零售的市场份额的增加，制造商的利润减少，无法拿出更多的成本投入到绿色研发中，制造商参与农产品生产的意愿降低，因此绿色度和批发价格均降低.

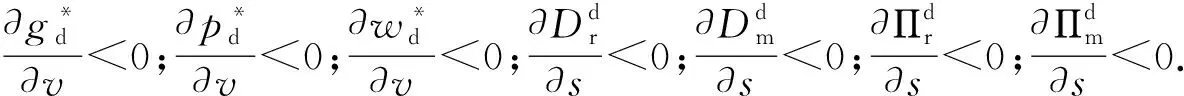
由命题3可知，两种决策模式变量的变化趋势一样，随着绿色研发的困难增加，农产品的绿色度、最优价格、销售数量以及整体供应链上的利润均下降.

2.4 数值仿真及分析

为了进一步验证模型的可行性，对变量进行赋值：Q=200；b=2；c=2；X=100；ur=0.1；um=1；σr=1.5；σm=1.2；rr=1；rm=0.8；v=5；z=5；α=5；β=3；b=2

2.4.1 线下零售市场份额对结果的影响

当s在0.25～0.65时，对比图1可知，集中决策模式下，随着市场份额的增加，最优绿色度和最优价格的值不变，而分散决策模式下，随着市场份额的增加而降低.对比图2可知，在集中决策模式下的供应链上的总利润和两个渠道的销量均高于分散决策模式下.表2、3将数据带入模型中，做进一步验证，同时命题1、2也得以论证.

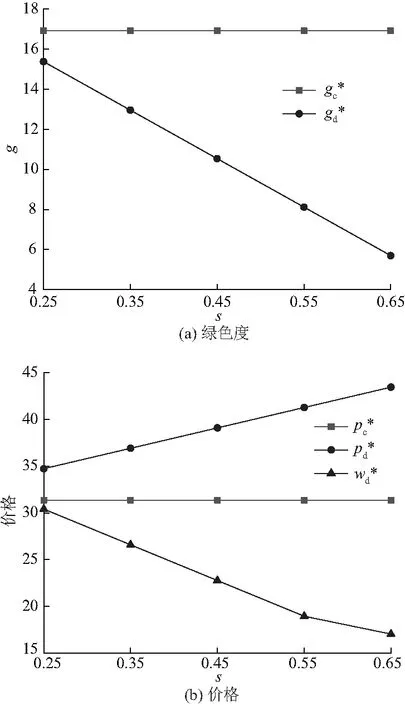
图1 最优绿色度和价格随市场份额的变化趋势

图2 双渠道利润和销售数量随市场份额变化的趋势

表2 集中决策模式下随s值变化变量最优值的变化

表3 分散决策模式下随s值变化变量最优值的变化

2.4.2 研发影响因子对结果的影响

当市场份额确定时，研究研发影响因子对结果的影响，赋值市场份额s=0.5，v取值(1,9).由图3、4可知，在两种决策模式下，最优绿色度、最优价格、销量以及成员利润均随着研发因子的增加而下降.

图3 最优绿色度和价格随研发影响因子的变化趋势

从图中可知，当研发困难加大时，利润若低于普通的农产品时，制造商将会放弃生产绿色农产品，因此制造商要研发新技术来降低困难，另外，政府也可以进行补贴给制造商，来激励制造商生产绿色农产品.表4、5也进一步验证以上结论，同时命题3也得以验证.

图4 双渠道销售数量和利润随研发影响因子的变化趋势

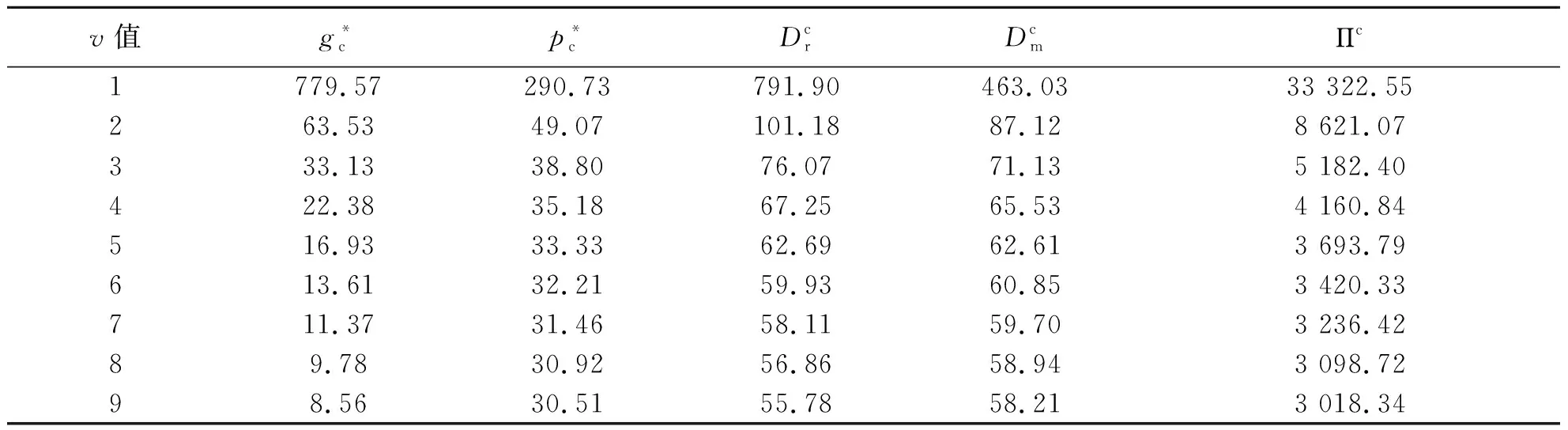
表4 集中决策模式下随v值变化变量最优值的变化

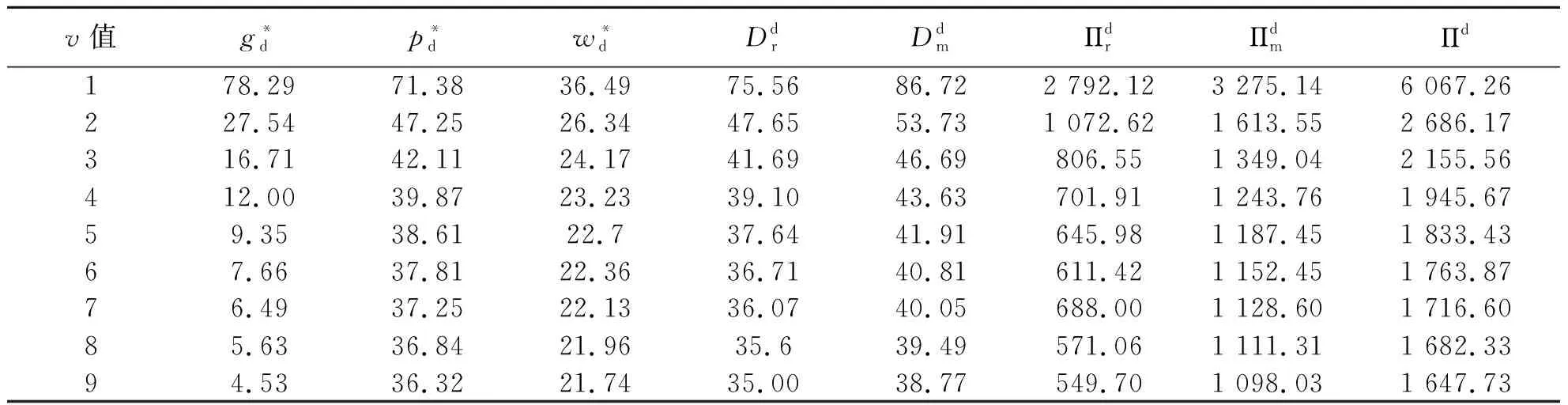
表5 分散决策模式下随v值变化变量最优值的变化

3 协调策略

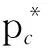
(26)

(27)

由式(4)可得契约批发价w′为:

(28)

(29)

X-βz2+F

(30)

(31)

(32)

F的大小，取决于供应链双方成员的议价能力.当F值较大时，对制造商有利；当F值较小时，对零售商有利，要减少制造商和零售商的利润冲突，只有当F在(F1，F2)时，供应链双方成员对利润分配才能达成一致，实现双赢.

4 结论

(1) 线上、线下所占市场份额的合理性是双渠道供应链存在的必要条件.在集中决策模式下，市场份额的变化不会影响各个变量的最优值，分散决策模式下，线下零售市场份额的增加，零售商参与绿色供应链的意愿加强，而制造商的意愿减弱.

(2) 集中决策模式下的最优绿色度、最优价格、销售量以及利润都要高于分散决策模式下.

(3) 为了促进供应链成员的合作，制定二阶段简单的契约机制来减少制造商和零售商的利润冲突，只有当F=(F1，F2)时，供应链双方成员对利润分配才能达成一致，实现双赢.

文中只是根据具体的情况而设计二部契约机制来促进成员之间的合作，模型是基于一定的假设之上：只是考虑一个制造商和一个零售商，现实中可能含有多个制造商和多个零售商；为了简化计算，只是将销售量等于生产量，但现实中可能还有库存或者缺失量，这将是以后的研究方向.