长三角城市群市场一体化与绿色发展效率：理论、测量与空间检验

陈立泰 籍 磊 李金林

[提要]寻求经济增长与环境改善的双赢已成为绿色发展的内在要求，而推动统一市场体系建设是实现经济增长、生态环境保护与提高绿色增长效率等目标的重要制度保障。本文基于市场一体化视角，首先探讨了市场一体化对绿色发展效率的作用机理，然后利用2004-2018年长三角城市群38个城市的面板数据，通过空间计量模型探讨了市场一体化对长三角城市群绿色发展效率的影响，得到以下结论：(1)总体来看，在2004年到2018年这一考察期内，长三角城市群大多数城市绿色发展效率水平值有了显著提高，但绿色发展效率不平衡发展的空间格局较为突出；(2)采用地理距离矩阵、经济矩阵以及地理距离和经济嵌套矩阵的空间计量模型回归结果显示，长三角城市群绿色发展效率的确存在显著正向空间交互效应，即当长三角城市群内相邻城市的绿色发展效率水平上升时，受影响城市的绿色发展效率水平也跟随上升；(3)从空间异质性来看，市场一体化对绿色发展效率的影响呈现出空间连片特征，上海、南京、苏州、扬州、杭州、温州、宁波以及合肥等城市，其中大多数城市经济比较发达，具有较大的系数。

改革开放40多年以来，中国依靠大规模投资迅速实现工业化和城市化，使得经济实现跨越式的增长，令全世界为之瞩目。但这种增长方式主要依靠大量劳动力和不可再生能源提供相应的支持，纯粹以“高消耗、高污染、低效益”为导向的粗放型发展尽管使得经济增长迅速，却未能实现其由“量”到“质”的突破，并且还使中国付出了沉重的环境代价。[1]由2018年CEEB相关报告的数据可知，中国338个地级市及以上城市中，仅有少量城市实现了环境空气治理达标，而环境空气质量未能达标的城市竟有高达64.2%。严重的环境污染对于居民个体而言不利于其生理健康，对于国家而言则降低了经济发展质量。[2]目前，绿色经济被认为是减少污染物排放、节约能源与实现经济可持续增长的有效途径。[3]同时，党的十九届五中全会提出，要大力推动经济社会发展全面绿色转型，促进绿色生产和生活方式的形成。因此，“既要绿水青山，也要金山银山”的发展模式成为学术界关注的焦点问题，[4]这不仅是高质量发展的内在要求，同时对于推动经济社会全面绿色转型也具有重要现实意义。

目前，推动统一市场体系建设是实现经济增长、生态环境保护与提高绿色增长效率等目标的重要制度保障。[5]为了打破市场分割的限制，促进区域资源要素实现自由流动，党中央和国务院先后出台了《京津冀协同发展规划纲要》《成渝城市群发展规划》《长江三角洲城市群发展规划》等一系列区域经济发展规划，且在上述规划中均明确要求城市群一体化发展，这也意味着区域一体化市场建设已成为中国政府的重要任务之一。[6]而长三角城市群作为中国工业化发展进程最快的地区之一，其不仅是中国经济发展的核心地区和战略支撑点，更是在推进区域实现“生态优先、绿色发展”过程中发挥示范作用。尤其是在《长江三角洲区域一体化发展规划纲要》里面特别强调长三角城市群内上海、浙江、江苏以及安徽应当重点围绕“生态环境”等领域展开相应合作，生态环境一体化发展必定会成为长三角城市群区域一体化发展过程中不可或缺的一环。[7]因此，促进长三角城市群三省一市整体绿色发展效率水平不断提升，缩小地区内部绿色发展效率差距，将成为长三角区域一体化进程中的必然选择。

就大多学者的研究而言，市场一体化能够显著促进经济增长。[8]从知识的维度来看，市场一体化可以通过对内要素和产品的交流以及相应的分工来缓解区域间知识错配，从而推进区域全要素生产率提升。[9]毛其淋和盛斌从区域市场整合的视角出发，实证检验了其对省际全要素生产率的影响。研究后发现，区域市场整合能够显著地促进全要素生产率水平的提升。[10]但是，在关注市场一体化所带来的经济效应的同时，也不能忽略市场一体化所产生的环境效应。从理论上来看，市场分割会导致资源错配，这将引起碳排放配置效率一定程度上的损失，进而在长期上会对碳排放强度带来不利的影响。当地方政府进行一体化合作时，区域间市场一体化水平逐渐提升，生产要素也能实现自由流动，这将极大推动城市群的节能减排效应，从而有力地增强城市群经济发展的整体质量。[11]然而，绿色可持续发展的内涵要求在实现经济增长的同时又能兼顾资源节约与生态环境保护，那么，长三角城市群市场一体化是否能满足这一要求——在实现经济增长的同时还能实现环境的友好？这不仅对进一步探索可重复、可扩展的绿色发展新路径来说显得尤为必要，且更决定了长三角城市群生态保护战略能否顺利实现。[12]如果上述问题得以证实，其背后又蕴含着怎样的作用机制？市场一体化对绿色发展效率的作用在本身特征及时空规律上又有何差异？本文尝试对上述问题进行深入的论证，以期为政府制定和调整政策提供现实依据。

一、理论分析

(一)绿色发展效率的内涵

绿色发展是作为破解自然环境约束以及经济实现绿色高质量发展转型难题的关键所在，[13]与其概念相似的还有可持续发展、绿色经济、绿色增长等相关概念。在1987年，“可持续发展”这一概念首次被世界环境与发展委员会提出，实质内涵是一方面不能危及后代发展所需，另一方面又能够满足当代人的发展所求。在2010年，绿色经济这一概念率先由联合国环境规划署明确给出，认为绿色经济的核心内涵一方面是其能够提升全世界人民的以及带来相应的社会公平，另一方面还能够极大地降低对环境的破坏。[14]随后，绿色增长这一具有更丰富内涵的衍生概念也逐渐出现。[15]尤其是2011年经济合作与发展组织明确指出绿色发展不单单是有利于实现经济增长，也还可以在防止环境破坏、生物丧失多样性等方面发挥至关重要的作用。同时，在2017年党的十九大报告中明确指出了中国要如何实现绿色发展的目标以及相应的实现方式，即绿色发展的核心内容是既强调要不断地实现经济增长，同时又要达到保护环境的目的，这是一种用高质量发展的理念来构建共同、协调、公平的可持续发展模式。[16]

绿色发展作为一种新的发展模式，循环、低碳、可持续是绿色发展的核心理念，其在本质上要求提高生态、环境和资源的综合利用效率，且更加注重效率、和谐和可持续性，即关键之处在于提升绿色发展效率。[17]绿色发展效率作为多数学者测度绿色发展水平的重要方法之一，若所测度的绿色发展效率数值越大，这就充分表明绿色发展水平越高。[18]其本质在于一方面不仅能够带来经济增长，另一方面还可以兼顾节能减排，[19]从而有力地推动由高投入、高排放和低产出转向绿色生产的发展方式，这与中国正深入推进的绿色发展转型的内在要求相契合。[20]

(二)市场一体化影响绿色发展效率的理论机制

对于目前中国的区域发展而言，市场一体化既是中国区域发展的主要趋势又是推动地区经济演变的重要引擎。[21]已有研究也表明，市场一体化不仅具有一定的经济效应，[22][23]而且还具有一定的环境影响效应。[24][25]因此，本节参照Ciccone 和Hall[26]、Ciccone[27]、林伯强和谭睿鹏[4]以及郭爱君和张娜[28]的做法，构建数理模型分析市场一体化影响绿色发展效率的作用机制。假设生产函数符合C-D形式，那么其生产函数可以由如下形式表示：

Y=AF(L，K)

(1)

其中，Y表示总产出，L表示劳动力投入，K表示资本投入。假设企业生产一种资本密集型产品Q，在生产产品Q的过程中会产生相应的污染排放P，从而产生负外部性。由科斯定理可知，当产权能够被清楚的界定时，企业就要为在生产过程中所排放物的污染物承担相应的费用。因此，理性的企业此时就会在现有生产资料约束情形下对正常产出和非期望产出做出选择从而实现自身的利润最大化。假设厂商用于减少非期望产出的生产资料占总生产资料的比例为θ，0≤θ≤1。当θ=0，F为企业的潜在生产能力，当0<θ≤1时，厂商用于生产的生产资料为1-θ，其实际产量为(1-θ)Y。因此，我们可以得到企业生产的期望产出和非期望产出的表达式为：

期望产出产量Q=(1-θ)AF(L，K)

(2)

污染排放量P=φ(θ)AF(L，K)

(3)

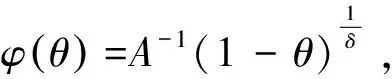
此时，借鉴张可[29]的做法，用非期望产出占正常产出的比重来表示污染排放强度ω，即将式(3)代入到式(2)可以得到污染排放强度，具体形式如下：

(4)

同时，本文在参考Hulten等[30]、刘生龙和胡鞍钢[31]以及毛其淋和盛斌[10]等学者的做法，我们假定A是多元组合，其具体形式为：

(5)

其中，A0表示初始的生产效率水平，segit表示市场一体化水平，ε表示的是市场一体化水平对生产率的影响弹性。

将(5)式带入到(4)式可以得到：

(6)

进一步，将式(6)左右两边同时对市场一体化求导数可得：

(7)

由(7)式可知，污染排放强度对市场一体化的一阶导数小于0，表明随着市场一体化水平的提升，污染排放强度逐渐减小。

二、长三角城市群绿色发展效率的时空特征分析

(一)长三角城市群绿色发展效率测度

1.测算方法

Charnes等[32]首次提出DEA方法之后，该方法就被大多数学者广泛运用于效率指标的测度当中，并且已成为评价相对效率的主要方法。然而，传统的DEA方法在评价决策单元效率的时候往往忽视了松弛变量所带来的影响，同时也未能考虑非期望产出，从而会引起测度的效率结果出现一定的偏差。就这些不足，Tone[33]又提出了非径向和非角度的SBM(Slacks-Based Measure)模型。此后，为了可以更全面地考虑投入、产出、污染三者之间的联系，Tone[34]又提出了加入非期望产出的SBM模型，从而不仅能够有效避免投入产出松弛性的问题，还能进一步处理在将污染排放等作为非期望产出存在下的效率评价问题。因此，SBM模型也被学者们广泛运用于生态效率、工业用水效率以及能源效率等领域。

因此，本文参照Li 和Hu[35]的做法，选择SBM模型所测度的最终变量来表示长三角城市绿色发展效率。其中，在SBM模型里面包含n个决策单元，而上述的投入变量(即x∈Rm)、期望产出变量(即yb∈Rs2)以及非期望产出变量(yb∈Rs2)都会包含在模型的每个决策单元里面。

X为投入变量所表示的矩阵(X>0)，X=[x1，x2，，，xn]∈Rm×n，Yg为期望产出变量所表示的矩阵(Yg>0)，Yg=[yg1，yg2，，，ygn]∈Rs1×n，Yb为非期望产出变量所表示的矩阵(Yb>0)，Yb=[y1b，y2b，，，ynb]∈Rs2×n，其中m、s1以及s2分别表示投入、期望产出和非期望产出的数量。绿色发展效率测度模型具体如下：

(8)

s.t.x0=Xλ+s-

(9)

y0g=Ygλ-sg

(10)

y0b=Ygb+sb

(11)

λ≥0，s-≥0，sg≥0，sb≥0

(12)

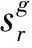
2.指标选取

根据前文的分析，并结合数据可得性原则，本文构建了绿色发展效率的测度指标体系，如表1所示，具体如下：非资源投入指标主要包括资本、劳动力、建成区面积、建成区绿化覆盖率。其中，资本投入：用固定资产代替资本存量的方法，采用全社会固定资产投资额作为资本投入量；劳动投入：采用全社会就业人数，即城镇单位就业人数、(私营/个体)就业人数的加总数来衡量；资源投入：采用天然气和液化石油气供应量来衡量；期望产出：用长三角城市群群内各城市当年国内生产总值(GDP)表示，非期望产出：用工业废水、工业二氧化硫、工业烟尘以及碳排放表示。

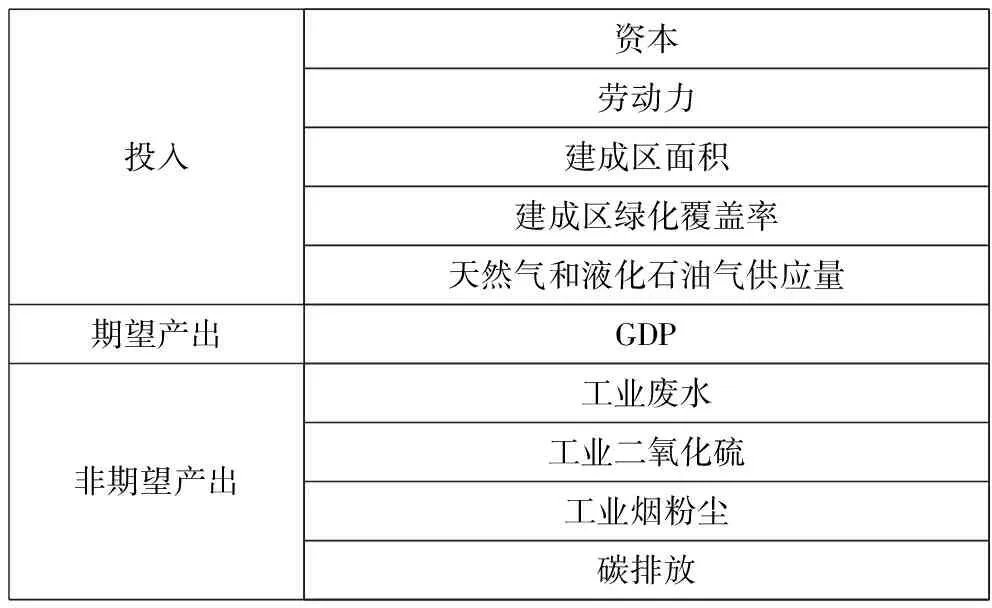
表1 绿色发展效率的指标体系

3.研究对象与数据来源

由于2019年正式出台的《长江三角洲区域一体化发展规划纲要》涵盖了长三角城市群内41个城市，其中，鉴于安徽省的六安市、池州市以及江苏省的淮安市缺失数据较多，本文最终研究对象为长三角城市群38座城市。本文研究时间跨度为2004-2018年，选取2018年作为研究的时间终点是因为当前各省市统计年鉴的最新公开年份是2020年，也即是各城市2019年的实际指标，但由于2019年有相当多的城市数据缺失，因此，本文将实际年份定在2018年。所需数据主要来源于国泰安数据库、《中国城市统计年鉴》《中国城市建设统计年鉴》以及《中国区域经济统计年鉴》，同时部分数据还使用了长三角城市群各省级和地级市历年统计年鉴和统计公报。此外，对于长三角城市群内某些城市数据存在个别的缺失值，本文采用插值法进行处理。

(二)长三角城市群绿色发展效率的区域差异及其分解

1.长三角城市群绿色发展效率的空间分布特征

为了更加直观地刻画长三角城市群各城市绿色发展效率的时空分异特征，本文基于地市级层面依次绘制了2004年、2009年、2014年以及2018年长三角城市群38座城市绿色发展效率的地区分布图。从图1可以看出，在2004-2018年间，长三角城市群绿色发展效率呈现出非均衡的状态，各城市之间绿色发展效率水平存在很大的区别。综合来看，2004年长三角城市群绿色发展效率水平最高的城市是浙江省的温州市，其绿色发展效率水平值达到了0.9971；其次是江苏省的镇江市和泰州市，绿色发展效率水平值分别达到了0.9948和0.9947；绿色发展效率水平最低的城市是安徽省的铜陵市，其值仅为0.4519，各城市绿色发展效率水平差距明显。从2009年的地图来看，相较于2004年，长三角城市群大多数城市绿色发展效率水平出现了小幅度的上涨，绿色发展效率水平在0.7或者以上的城市明显多于2004年。从2014年到2018年这两年的地图来看，长三角城市群大多数城市绿色发展效率水平值有了显著的提高，2014年绿色发展效率水平值超过0.8的城市达到了21座，而2018年绿色发展效率水平值超过0.8的城市甚至高达28座。可能的原因在于，在这一时期国务院印发了《长江三角洲城市群发展规划》，这极大有利于实现长三角城市群产业合理分工，优化各城市的产出结构，并且可以实现生态环境的协同治理，进而大幅度提升长三角城市群各城市绿色发展效率水平。

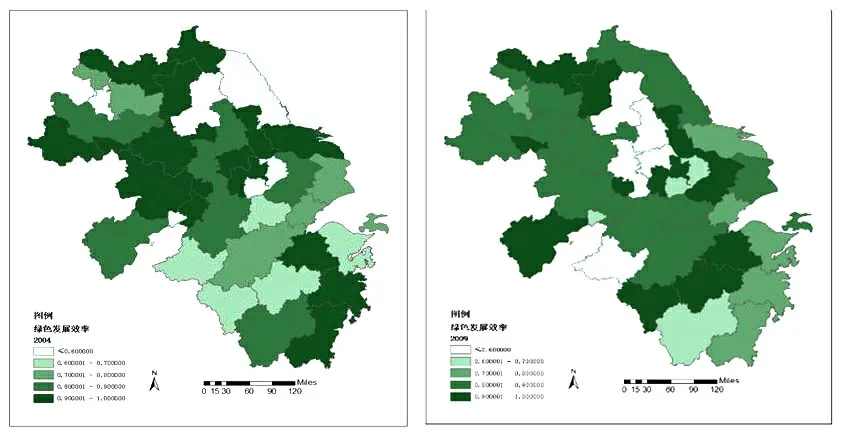
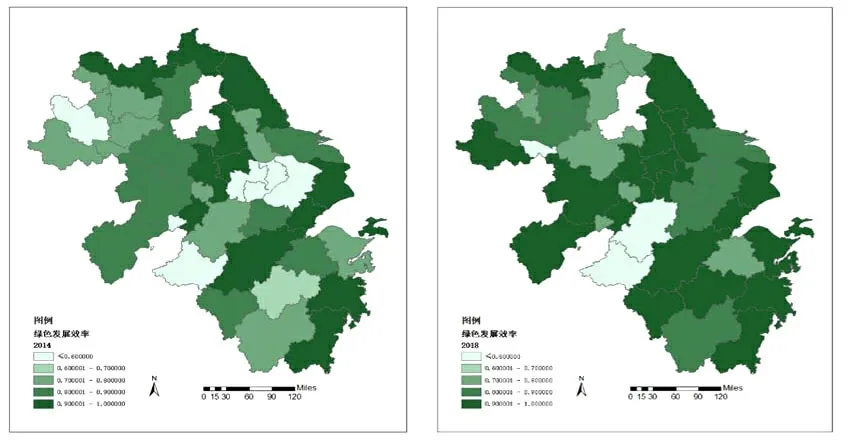
图1 2004-2018年长三角城市群各城市绿色发展效率

省际层面来看，本文选择将长三角城市群各城市绿色发展效率取平均值得到相应省的绿色发展效率水平值。图2 描绘了历年长三角城市群各省(直辖市)绿色发展效率的变动过程。大致地看，长三角城市群总体、上海市、浙江省、江苏省以及安徽省绿色发展效率均出现了“上升-下降-上升-下降”的M型波动趋势。同时，绿色发展效率水平在各省(直辖市)之间存在着明显的差异。江苏省绿色发展效率平均水平大多年份处于领先地位，且大多数年份也高于同期长三角城市群总体绿色发展效率平均水平；上海市则前期绿色发展效率水平值相对较低，在2014年以后，其绿色发展效率水平值持续上升，至2018年已位居长三角城市绿色发展效率水平第一位；浙江省绿色发展效率水平大多年份也高于同期长三角城市群总体绿色发展效率水平的平均值，且与同期江苏省绿色发展效率水平相近；安徽省绿色发展效率大多年份均处于长三角城市群总体绿色发展效率水平之下。

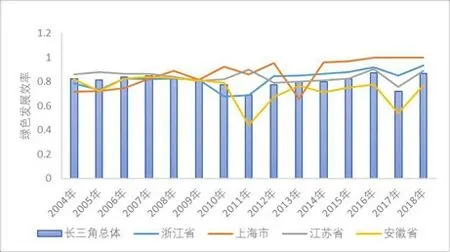
图2 2004-2018年长三角城市群省级绿色发展效率

进一步，根据行政划分依据，按照省际层面测算长三角城市群内38座城市绿色发展效率水平的标准差，可以动态描述长三角城市群各城市之间绿色发展效率的差距变化(如图3所示)。由于上海市是直辖市，其绿色发展效率的标准差始终为0，因此本文未将上海市纳入省际对比中。总体来看，浙江省、江苏省以及安徽省各城市在2004-2018年内绿色发展效率水平表现出鲜明的波动过程，大致由2004-2009年、2009-2011年以及2012-2017年三波段组成，依次呈现出绿色发展效率差距持续缩小-逐渐扩大-持续缩小的演变。从省际层面来看，江苏省绿色发展效率水平的标准差多数年份均小于长三角城市群总体标准差，这表明江苏省内部各城市绿色发展效率水平差距相对于其他省城市波动较小；而安徽省多数年份绿色发展效率水平的标准差大于长三角城市群总体标准差，这表明安徽省内各城市绿色发展效率水平差距较大；浙江省内各城市绿色发展效率水平差距变化趋势在2004-2014年这一时间段内与江苏省大体相似，2014年以后，浙江省内各城市绿色发展效率水平差异性快速拉大，并且超过了江苏省。

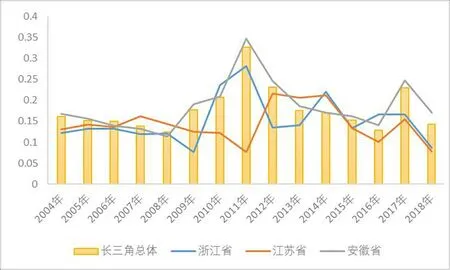
图3 长三角城市群城市间绿色发展效率水平标准差(2004-2018年)

2.长三角城市群绿色发展效率地区差异的分解及其来源

从现有的研究来看，对绿色发展效率水平的空间非均衡性测度通常可以采用基尼系数以及泰尔指数等常用指标，但上述方法不能有效解决诸如样本数据的交叉重叠等问题。[36]而Dagum基尼系数分解在对变量进行描述时，可以对变量的区域内、区域间差距进行分解，不仅能够更加全面反映变量的区域差异问题，同时，也还可以有效解决上述方法所忽略的问题。[37]因此，本文选择 Dagum基尼系数分解法来测度长三角城市群绿色发展效率区域差异。其相应的计算公式如下所示：

G=Gω+Grb+Gt

(13)

(14)

μh≤μj≤...≤μk

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

从上式(13)可以看出，测算出的长三角城市群绿色发展效率总体基尼系数(G)等于长三角城市群内各省(直辖市)区域内差异贡献(Gω)、各省(直辖市)区域间净值差异贡献(Grb)，以及各省超变密度贡献(Gt)三者之和。上述中公式(14)、公式(17)、公式(19)以及公式(20)分别反映的是长三角城市群绿色发展效率的总体基尼系数(G)、区域内差异贡献(Gω)、区域间净值差异贡献(Grb)及超变密度贡献(Gt)测算公式。各公式均基于长三角城市群绿色发展效率水平值做了平均处理，因此，Dagum基尼系数即反映了长三角城市群绿色发展效率水平相对差异的大小及来源情况。公式(15)依据长三角各省(直辖市)绿色发展效率指标的均值对其进行了排序；公式(16)和公式(18)分别表示长三角城市群各省(直辖市)区域内基尼系数Gjj、区域间基尼系数Gjh。其中，yji(yhr)为第j(h)个省份(直辖市)任一城市的绿色发展效率指标，μ为长三角城市群绿色发展效率指标平均值，n为城市个数，k为省份(直辖市)个数，nj(nh)为第j(h)个省份(直辖市)内部城市个数，pj=nj/n，sj=njμj/nμ；公式(21)中Djh为j、h个省份(直辖市)之间绿色发展效率指标的相对影响；公式(22)中djh表示区域绿色发展效率指标的差值，可认为长三角城市群第j、h个省份(直辖市)中所有yji-yhr>0的样本值加总的数学期望；公式(23)中pjh为超变一阶矩，表示长三角城市群第j、h个省份(直辖市)中所有yhr-yji>0的样本值加总的数学期望。其中，Fj(Fh)为长三角城市群中第j(h)个省份(直辖市)的累积密度分布函数。

根据上述方法，本文分别测算出了长三角城市群三省一市2004—2018年的绿色发展效率水平的总体变化差异及其来源，并从多个角度对其进行了深入分析。

(1)长三角城市群绿色发展效率水平的总体及区域内差异

由于上海市作为一个单独的直辖市存在，所以本文没有测度其内部绿色发展效率水平的差异，最终只测度了长三角城市群总体、浙江省、江苏省以及安徽省内部绿色发展效率差异。图4反映了2004-2018年长三角城市群总体以及三省内部绿色发展效率水平差异的变化趋势，具体数值见表3.2所示。

由图4和表2可以看出，长三角城市群绿色发展效率水平总体差异较大，总体的基尼系数分布范围在0.0774-0.1759之间。长三角城市群总体绿色发展效率水平的基尼系数在2004-2018年之间出现了M型的波动，其阶段性趋势现象尤为明显。其中，在2004-2009年间，经历了小幅的上升-下降-上升的趋势，而在2009-2018年则经历了下降-上升-下降的变化趋势。就长三角城市群区域内差异而言，长三角城市群内的浙江省、江苏省以及安徽省的绿色发展效率水平在其各自区域内差距位于不同的水平，但是并没有呈现出明显的差异化演变趋势。在2004-2018年考察期间内，安徽省的区域内差异的平均值最大，达到了0.1236；其次是浙江省区域内差异的平均值，达到了0.1059；江苏省区域内差异的平均值则最小，仅为0.0992。因此，由以上数据可以看出，安徽省区域内的绿色发展效率水平值差异最大，浙江省区域内绿色发展效率水平值差异则次之，江苏省区域内绿色发展效率水平值差异最小。此外，在2004-2018年间，浙江省、江苏省以及安徽省的区域内差异呈现出波动式上升趋势，三省在这段考察期内的区域内差异年均分别增长了0.91%、2.30%以及1.55%。显然，尽管江苏省区域内差异平均值在长三角三省中最低，但其差异却有可能存在显著增大趋势，因此，对江苏省绿色发展效率的区域内差异有必要实施更为有效的控制。

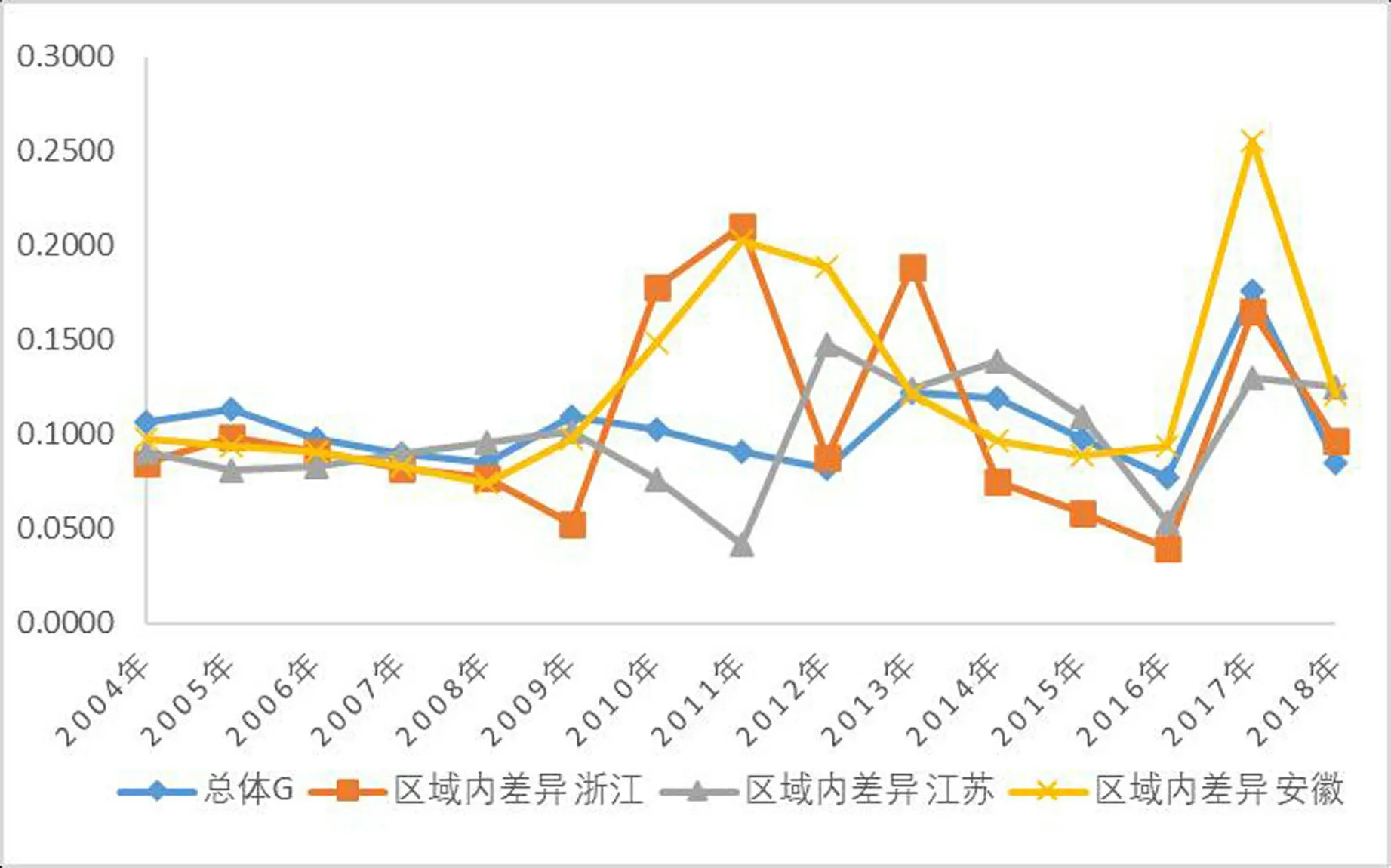
图4 长三角城市群绿色发展效率总体及区域内基尼系数的变化趋势

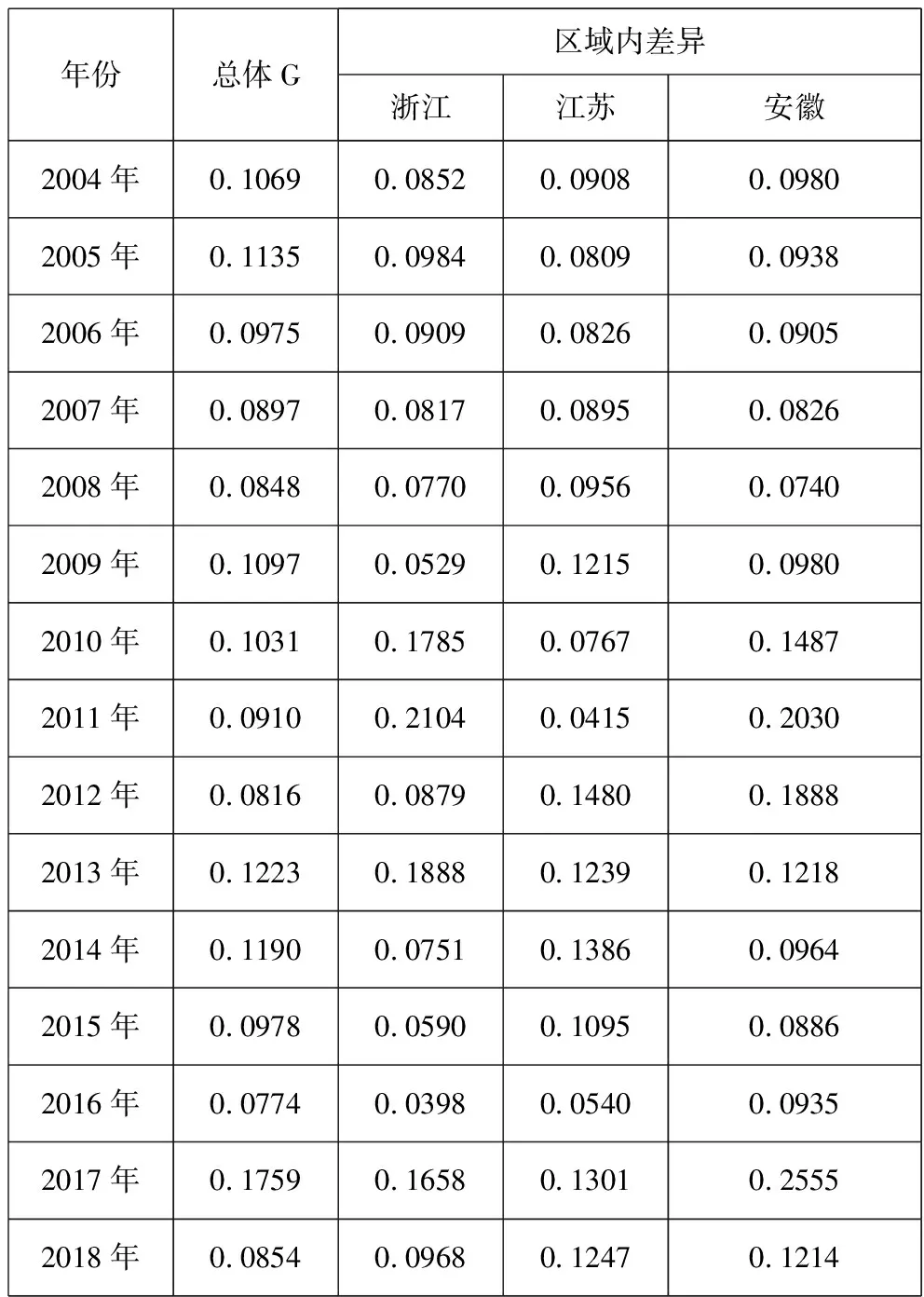
表2 长三角城市群绿色发展效率总体及区域内基尼系数

(2)长三角城市群绿色发展效率水平的区域间差异

长三角城市群中浙江省、江苏省以及安徽省绿色发展效率水平的区域间差异大小如图5和表3所示。从总体来看，浙江省与江苏省、浙江省与安徽省以及江苏省与安徽省区域之间的差异变动趋势大体相似，均经历了上升-下降-上升-下降的循环往复过程，在2004-2018年间，从图的变化趋势可以明显地看出，浙江和江苏的区域间差异小于浙江与安徽、江苏与安徽的区域间差距。同时，通过计算2004-2018年浙江和江苏的区域、浙江与安徽、江苏与安徽区域间差异的平均值分别为0.1088、0.1350和0.1413，由此可以看出，浙江和江苏区域间差异最小，这表明浙江省和江苏省在共同促进区域实现绿色发展方面的协同性相对较强。江苏与安徽区域间差距最大，这也表明两省份之间在共同促进绿色发展方面存在较弱的协同性。

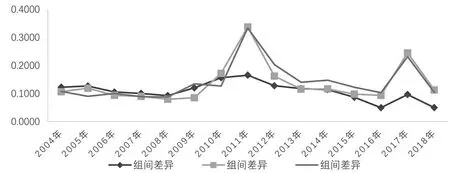
图5 长三角城市群绿色发展效率的区域间基尼系数

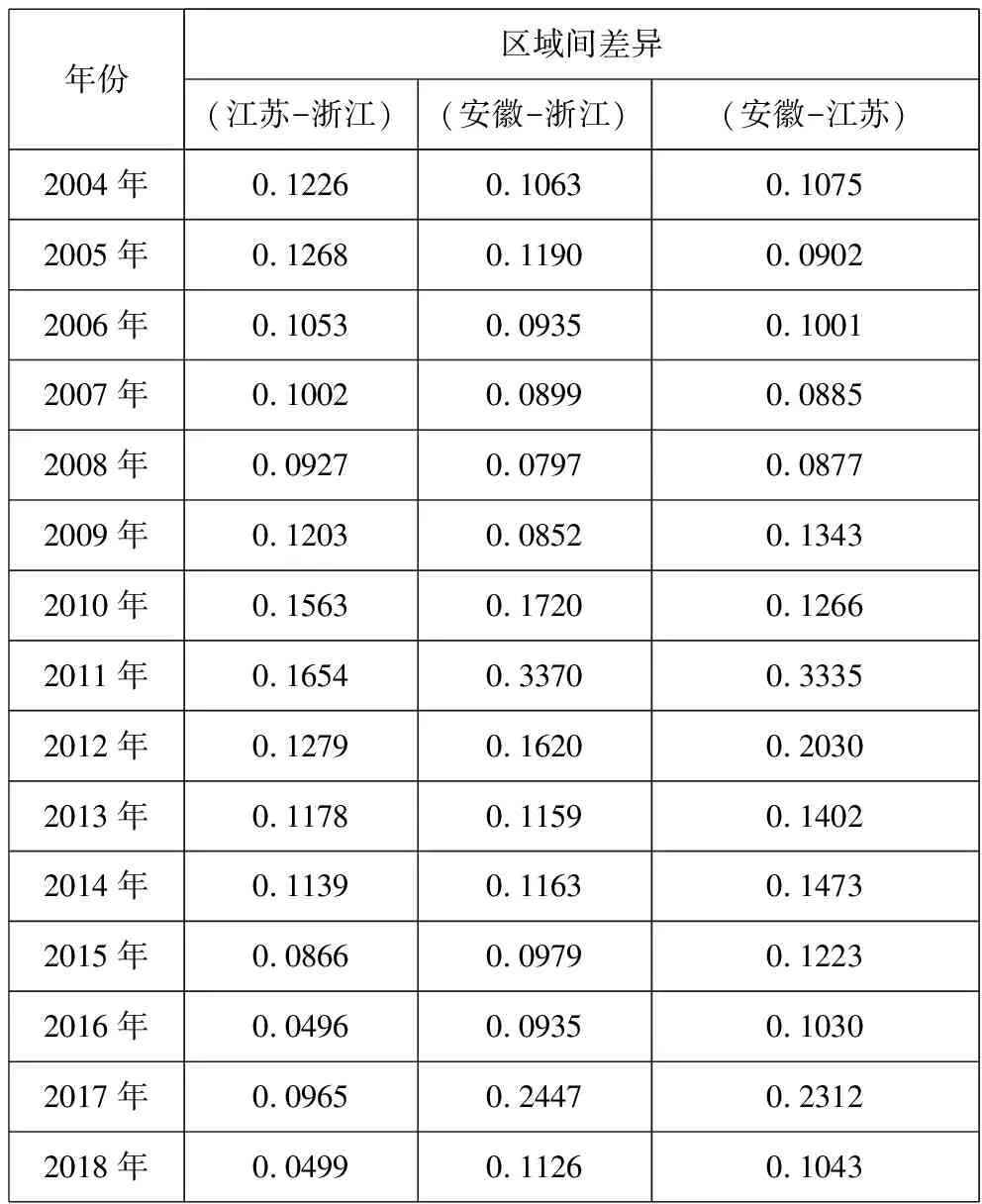
表3 长三角城市群绿色发展效率的区域间基尼系数

(3)长三角城市群绿色发展效率水平的差异及其来源

长三角城市群绿色发展效率水平的差异来源及其贡献如图6和表4所示。由图6可以看出，长三角城市群绿色发展效率的区域内差异来源及其贡献率在2004-2018年这一考察期内出现了一定程度的波动，但整体上来看变化相对较小；而区域间差异来源和超变密度则是反复出现上升-下降这一波动式的发展趋势。从三者的贡献大小来看，在2004-2018年期间，区域内差异、区域间差异以及超变密度的平均贡献值大小分别为0.0310、0.0469以及0.0257，而其平均贡献率则分别为30.01%、45.80%和24.19%。从以上数值可以看出，无论是贡献的平均值大小还是贡献率的大小，区域间差异均显著超过了区域内和超变密度，这充分反映了区域间贡献对于长三角城市群绿色发展效率总体区域差异至关重要，而区域内差异以及超变密度则分别紧随其后，由此可知，缩小各省(直辖市)区域间差异是解决长三角城市群绿色发展效率区域不均衡问题的重要途径。

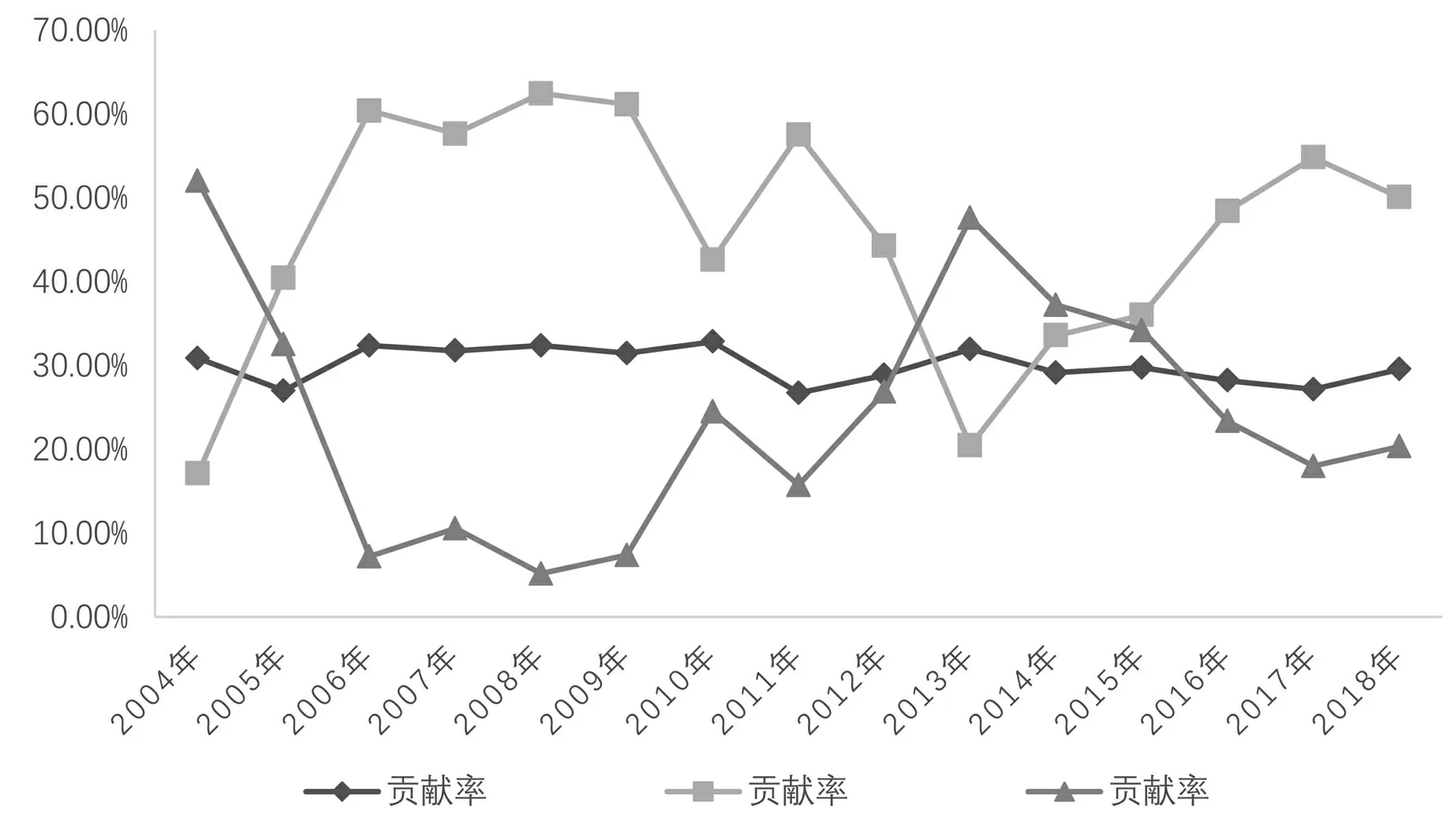
图6 长三角城市群绿色发展效率的差异来源贡献变化态势

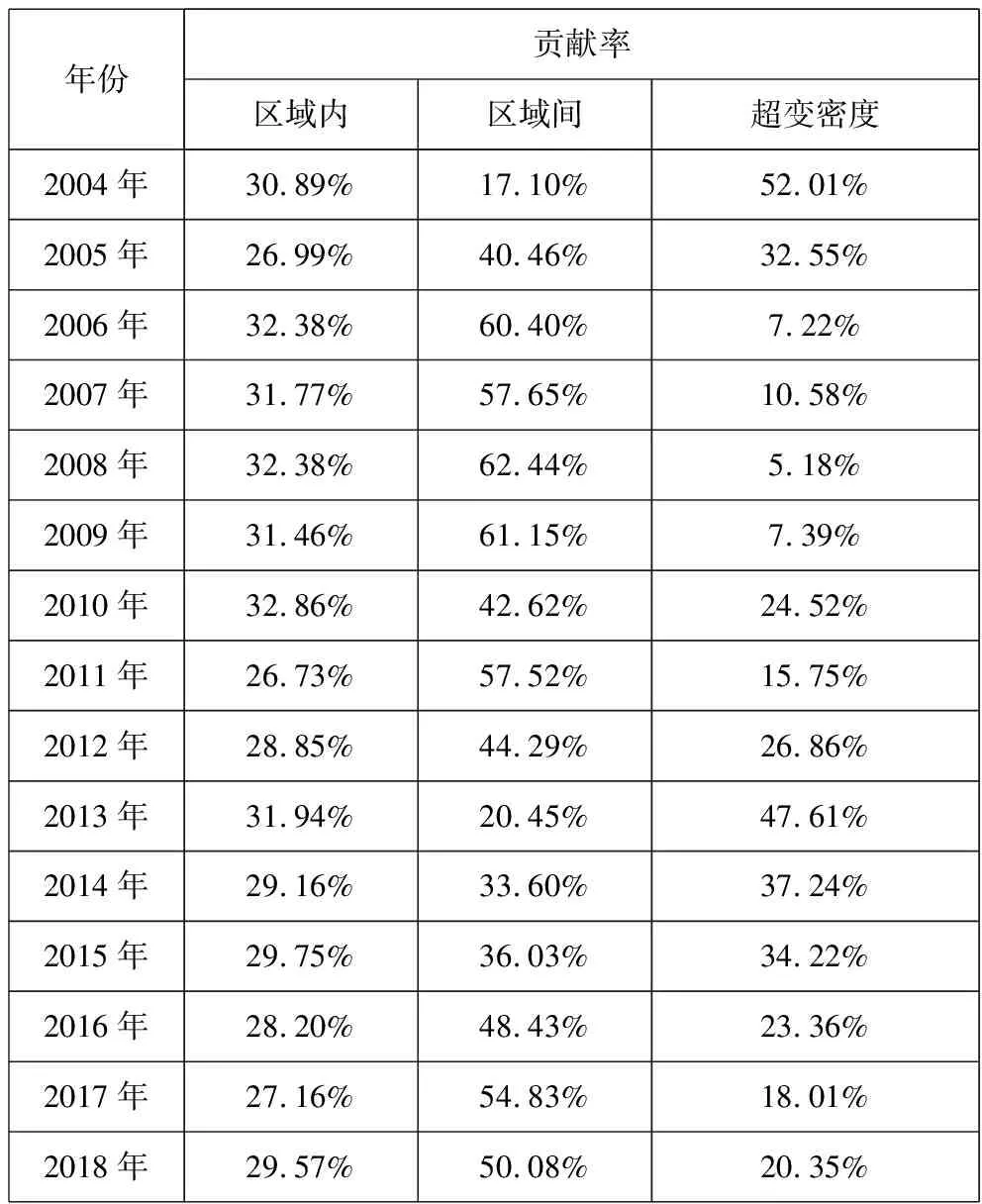
表4 长三角城市群绿色发展效率的差异来源及其贡献度

三、长三角城市群市场一体化对绿色发展效率的空间效应实证分析

已有研究表明，如果忽略一体化活动所带来的空间外溢效应这一现象，那么就很有可能会导致实证回归结果与现实出现较大偏差，[38]同时，中国省际之间的绿色发展效率也存在显著的空间关联性。[17]尤其近年来随着空间计量经济学的快速发展与广泛运用，越来越多的学者开始在研究绿色发展相关问题时考虑空间因素。[39]因此，本文有必要考虑空间因素的影响。

(一)空间自相关的识别

一般而言，在采用空间计量模型进行实证回归前，首先应当考察绿色发展效率是否存在空间相关性，而多数文献通常采用Moran’s I指数来判断变量是否具有空间相关性，而Moran’s I指数又可以分为全局Moran’s I指数和局部Moran’s I指数。具体方法如下：

1.全局Moran’s I指数

其相应的计算公式如下式(5.)所示：

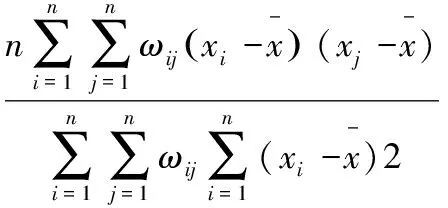
(24)

其中，n代表长三角城市群内的城市数量，xi和xj分别代表长三角城市群内城市i和城市j的绿色发展效率水平值，ωij则对应着的是空间权重矩阵，反映的是长三角城市群内城市i和城市j的临近关系，具体而言，当长三角城市群内城市i和城市j处于相邻位置时，则ωij的取值为1，当它们位置不相邻时，则ωij的取值为0。

全局Moran’s I指数在[-1，1]区间范围内变化，当全局Moran’s I指数的取值大于0时，这代表着长三角城市群内各城市绿色发展效率之间具有正相关关系，其数值与1越接近则表明空间关系越密切。当该指数取值为0时，则表示长三角城市群内各城市绿色发展效率之间不存在空间相关关系。当该指数取值小于0时，则表示长三角城市群内各城市绿色发展效率之间具有负相关关系，研究时空内的绿色发展效率水平值是随机分布的。

2.局部Moran’s I指数

该指数的计算公式如下式(25)所示：

(25)

其中，局部Moran’s I指数反映的是长三角城市群内城市i的绿色发展效率水平值与周边城市的关联程度。通过长三角城市群内各城市的绿色发展效率水平值可制作出“局部Moran’s I指数散点图”。其中，第一象限表示长三角城市群内绿色发展效率水平值较高的城市被其他绿色发展效率水平值较高的城市包围，即(高-高)型；第二象限则表示长三角城市群内绿色发展效率水平值较低城市被其他绿色发展效率水平值较高的城市包围，即(低-高)型；第三象限表示长三角城市群内绿色发展效率水平值较低城市被其他绿色发展效率水平值较低城市包围，即(低-低)型；第四象限表示长三角城市群内绿色发展效率水平值较高城市被其他绿色发展效率水平值较低城市包围，即(高-低)型。

3.绿色发展效率的全局Moran’s I指数测算结果

根据上述计算方法，本小节计算出了长三角城市群2004-2018年绿色发展效率水平的全局moran’s I指数及其统计分布特征，具体情况如下表5所示。

表5 长三角城市群绿色发展效率的Moran’s I空间自相关检验结果

从上表5的结果可以看出，长三角城市群绿色发展效率的Moran’s I值在考察期内一直保持显著为正，大多数年份在1%的显著性水平上显著。这充分说明了长三角城市群绿色发展效率存在明显的空间自相关性，且长三角城市群内绿色发展效率水平值较高的城市更加可能接近其他绿色发展效率水平值较高的城市。

4.绿色发展效率的局部Moran’s I 散点图

由上述长三角城市群绿色发展效率的全局 Moran’s I指数反映了绿色发展效率的整体空间相关性，但其忽视了长三角城市群内具体城市的空间特征，为进一步直观反映长三角城市群绿色发展效率的局部特征，本小节特刻画了绿色发展效率的局部Moran’s I散点图，但为了与前述内容保持一致性，本小节仅展示2004年、2009年、2014年以及2018年绿色发展效率的局部Moran’s I散点图。

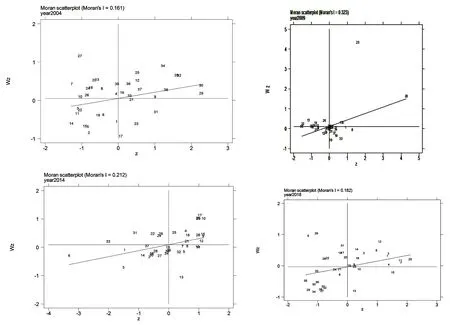
图7 2004年-2018年长三角城市群绿色发展效率Moran’s I散点图

从上图7所反映的结果我们可以清楚地看出，相较于2004年的Moran’s I值，2018年的Moran’s I值有一定程度的上升，且长三角城市群内多数城市处在第一象限和第三象限内，这充分说明长三角城市群绿色发展效率水平值存在比较明显的高高聚集和低低聚集的特征，但这种集聚现象并没有随着时间的推移而发生根本性的改变。

(二)空间计量模型设定

本小节根据上述分析，参照于斌斌[40]的做法建立空间滞后模型(26)与空间误差模型(式27和式28)对前文的理论假设展开实证检验。具体模型如下：

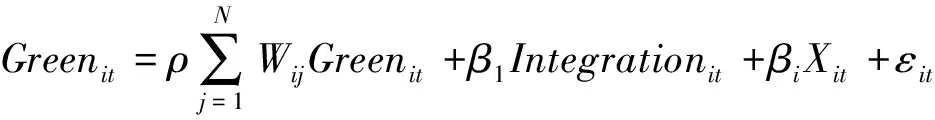
(26)

Greenit=δ1Integrationit+δiXit+φit

(27)

(28)

上述公式(26)-(28)为市场一体化对绿色发展效率空间影响的主效应。其中，Wij表示空间权重矩阵。t表示时期，i代表城市，εit则表示随机误差项，ρ表示空间滞后模型回归系数，λ则表示空间误差模型回归系数，Wij表示空间权重矩阵。本文参照韩峰和阳立高[41]设立了三种空间权重矩阵，分别为地理距离矩阵、经济矩阵以及地理距离和经济嵌套矩阵。权重矩阵的设置具体说明如下：

地理距离矩阵(Wdistance)：其中，Wij=1/dij，而dij表示长三角城市群内两两城市间的距离，对角线元素Wij=0。

经济矩阵(Weconomic)：采用长三角城市群内两个城市人均GDP差值之差的绝对值倒数来表示经济空间权重矩阵，即wij=(1/|xi-xj|)。

地理距离和经济嵌套矩阵(Wnested)：Wnested=φWdistance+(1-φ)Weconomic，其中φ表示地理距离矩阵的权重，且其取值范围为0<φ<1。参照邵帅等(2016)的做法，本文将φ的值取 0.5。该矩阵进一步表示了空间个体在地理和经济上的双重空间邻近性。

(三)指标选取

1.被解释变量

绿色发展效率(green)：根据第三章以SBM模型所测度的数值作为其代理变量。

2.核心解释变量

市场一体化(Integration)：目前大多文献在测度时主要采用商品市场价格指数或者劳动力市场价格指数这种相对单一的指标来衡量市场一体化程度，[42]但通过这样得到市场一体化程度只能单一地反映商品市场或者劳动力市场，不能有效反映中国各大市场之间的空间联动效应。因此，本文在参考赵奇伟和熊性美[43]做法基础之上，将市场一体化范围拓展到了商品市场、劳动力市场以及金融市场。同时参照李增福等[44]的做法，首先采用商品价格指数、职工平均实际工资指数以及FH指数分别测算出三个子市场的市场一体化程度，接着再通过主成分分析法计算出综合市场一体化指数(Integration)。综上所述，长三角城市群市场一体化指数的具体计算过程如下：首先，采用相对价格法来测度商品市场一体化程度(Commodity)；其次，参照都阳和蔡昉[45]采用工资趋同的做法来测度长三角城市群劳动力市场一体化水平(Labor)；再次，利用有条件的投资率与储蓄率的相关性(FH系数)来衡量长三角城市群金融市场一体化水平；[46]最后，利用主成分分析法得到商品市场一体化、劳动市场一体化以及金融市场一体化指数的主成分，从而最终得到长三角城市群综合市场一体化水平指数。

3.控制变量

参照李江龙等[47]、林伯强等[4]相关研究，选取控制变量：(1)固定资产投资(inv)：用各地区固定资产投资总额与各地市的生产总值之比表示。(2)外商直接投资(fdi)：选择外商实际投资额占其实际GDP的比重来衡量。(3)政府干预程度(gov)：选择财政支出占其实际GDP的比重来衡量。(4)环境规制程度(rate)：选择工业固体废物综合利用率来衡量，即该指标越高，那么代表环境规制程度则越强。(5)城市经济发展水平(gdp)：选择实际人均gdp来衡量。其中，采用以2004年为基期对各城市的人均 GDP做相应平减，从而得到各城市实际人均GDP；(6)城镇化水平(city)：选择用各城市城镇人口占总人口的比重来表示。

4.数据来源

选取2004-2018年长三角城市群38个地级市及以上城市作为样本进行实证分析。所需数据来源于长三角城市群内各省级和地级市统计年鉴和统计公报，以及国泰安数据库、《中国城市统计年鉴》《中国区域经济统计年鉴》《中国城市建设统计年鉴》等，由作者查阅、整理或价格平减测算获得。此外，为避免在实证检验过程中受到异常值的影响，本文对所有连续变量进行 1%的缩尾处理。

(四)空间计量模型估计结果及分析

1.基本回归结果分析

基于长三角城市群38个城市2004-2018年的面板数据，并且采用上述三种权重矩阵，将市场一体化作为解释变量带入基本模型进行回归。同时，对于本文选择空间滞后模型(SAR)还是选择空间误差模型(SEM)，通过比较空间滞后模型的LM-Lag统计、Robust-LM-Lag统计量和空间误差模型的LM-Error统计量、Robust-LM-Error统计量可以做出相应的选择，本文的模型无论比较哪一个统计量，空间误差模型的统计量更优，因此，本文采用空间误差模型作为基本空间计量回归模型。

由表6的回归结果可以看出：首先，第(1)列—第(3)列分别表示采用地理距离矩阵、经济矩阵以及地理距离和经济嵌套矩阵时市场一体化对绿色发展效率影响的空间效应，其回归系数分别为0.0532、0.0713以及0.0839，且分别在1%、5%以及5%的显著性水平上显著，这充分说明市场一体化在考虑空间效应时，其对绿色发展效率的影响依然显著为正。其次，长三角城市群绿色发展效率存在显著的正向空间互动效应。从空间误差的系数估计值来看，以市场一体化作为自变量的空间误差系数λ估计值都为正，且在 1%的显著性水平上通过了检验，表明绿色发展效率的确存在显著的正向空间交互效应，即当长三角城市群内相邻城市的绿色发展效率水平上升时，受影响城市的绿色发展效率水平也跟随上升。

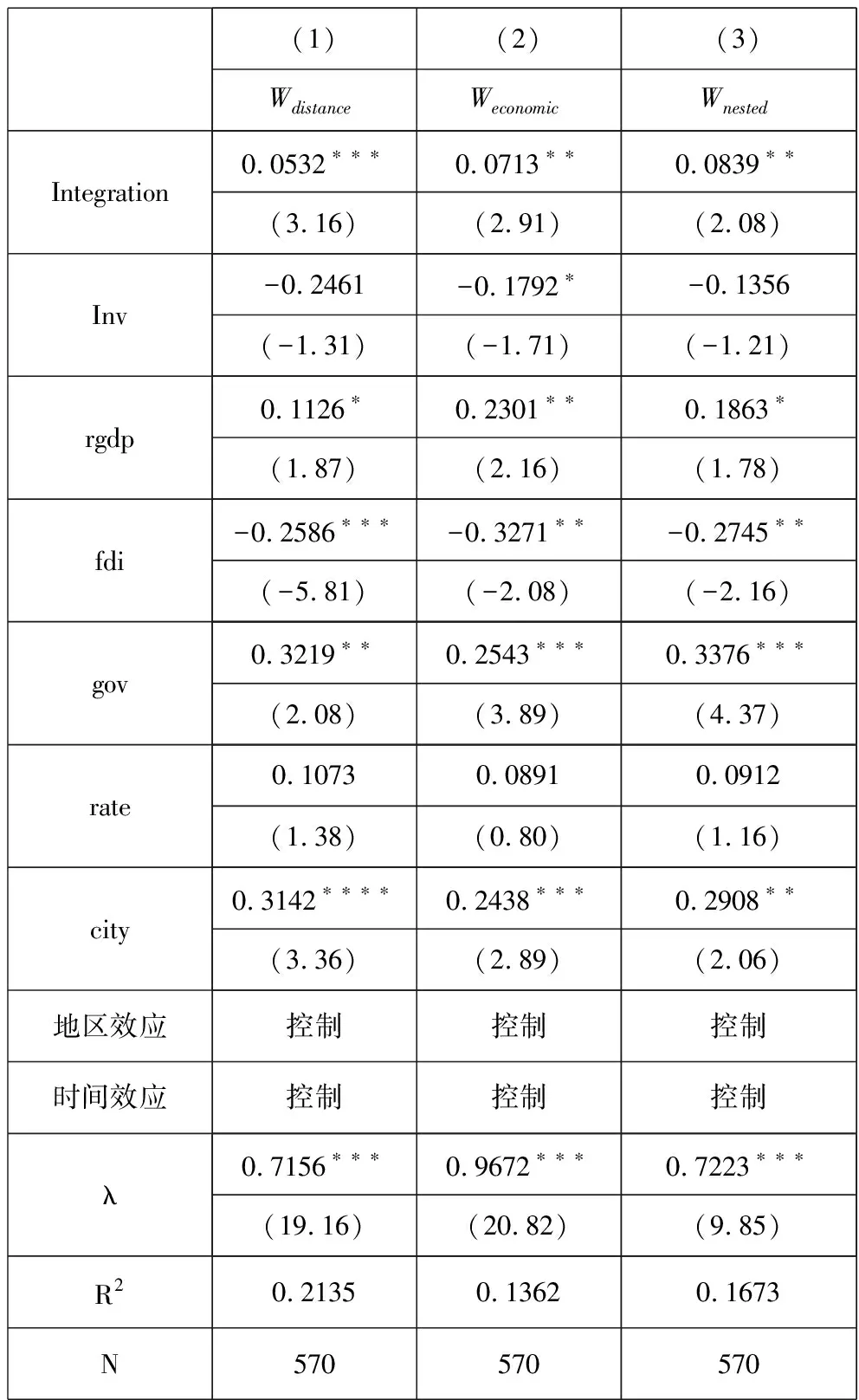
表6 空间计量模型回归结果

2.异质性分析

由于不同地区的生态环境指标存在空间效应，[48]且地区间资源禀赋、区位条件、经济基础、历史发展等因素存在异质性，市场一体化对绿色发展效率的作用关系不可避免地会受到来自这些区域异质因素的影响，因此在回归中必须考虑自变量系数为非常数这种可能性的存在，故本文选用地理加权回归(GWR)模型参数估计来考察市场一体化对绿色发展效率作用机制问题，既考虑相关解释变量的空间关联性，又考虑不同地区各项影响作用系数的异质性。GWR模型一般表达式为：

(29)

其中，Greenit表示被解释变量绿色发展效率，xit表示解释变量，所有变量与前文指标一致。(ui，vi)是第i个样本点的空间坐标，βj系数的下标j表示与观测值联系的m×1阶待估参数向量，是关于地理位置(ui，vi)的k+1元函数。GWR可以对每个观测值估计出k个参数向量的估计值，εi是第i个区域的随机误差项。

本文选择了2004年、2009年、2014年以及2018年的数据来分析长三角城市群市场一体化影响绿色发展效率的空间异质性，由于篇幅限制不全部列出所有年份。表7是2004年、2009年、2014年和2018年市场一体化与绿色发展效率的回归结果。

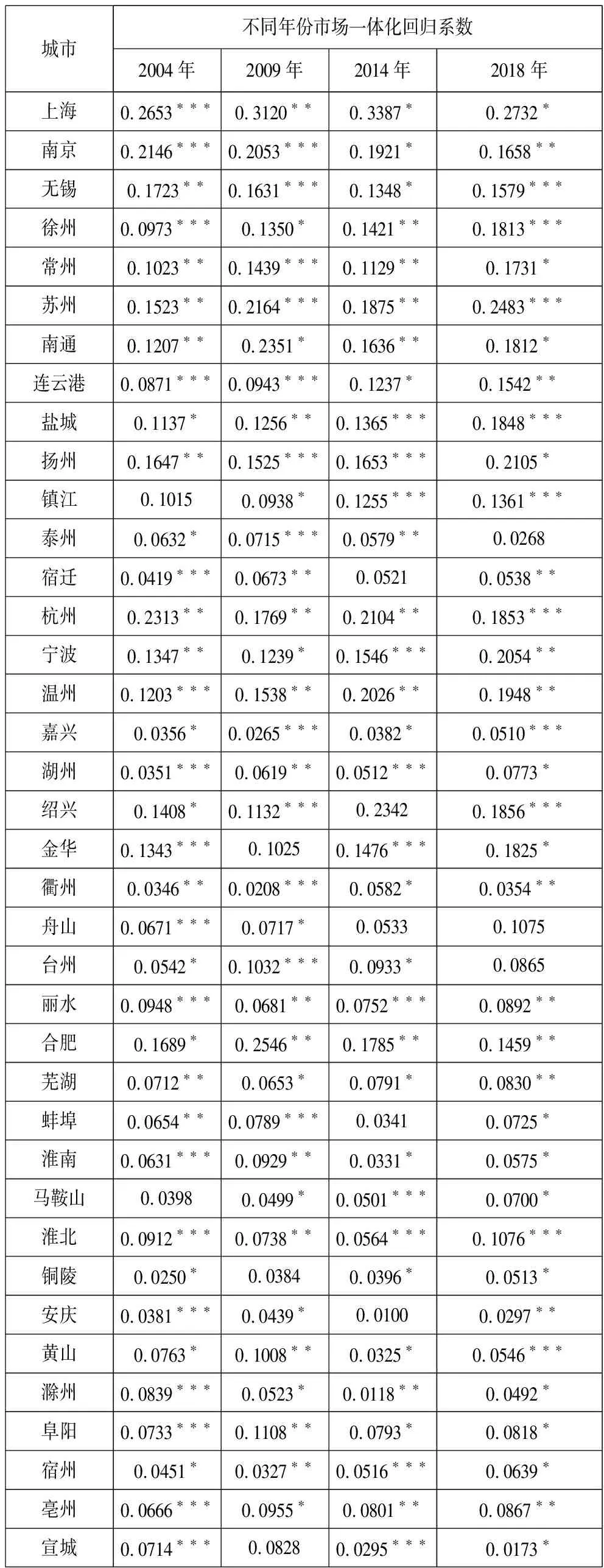
表7 市场一体化对绿色发展效率影响的GWR参数估计结果

从表7的回归结果可以看出：第一，市场一体化与绿色发展效率成正比，且从回归的系数来看，各城市市场一体化系数相差较大，这也说明长三角城市群各城市资源禀赋因素差异对本地区绿色发展效率有影响。第二，市场一体化对绿色发展效率的影响呈现出空间连片特征，上海、江苏与浙江三省(直辖市)回归系数普遍较高，其可能的原因是，在市场机制的作用下，弱化了该区域间存在的市场壁垒，提升了企业的增长效率，从而增强了该区域绿色发展水平。上海、南京、苏州、扬州、杭州、温州、宁波以及合肥等城市，其中大多数城市经济比较发达，具有较大的系数，深层次的机制离不开省份城市的梯度分布差异，经济相对发达地区市场一体化水平较高，地方保护主义减少，那么较低的购买成本会增加地区外同类产品的比较优势，从而加大购买地区外产品以替代本地生产，这将进一步减少污染产业在本地区所占的比例，从而大幅度提升了城市绿色发展效率。

3.稳健性检验

为了确保市场一体化影响绿色发展效率的回归结果稳健可靠，本文主要采用被解释变量替换、安慰剂检验的处理方式，进行稳健性检验。首先，参照刘杨等[18]的做法，选择资本、能源、劳动力以及技术等4个变量作为对应的投入变量，选择长三角城市群内各城市的GDP作为期望产出，同时选择工业三废以及碳排放作为非期望产出，进一步对被解释变量进行重新测度。将测得的指标作为前文的被解释变量替代指标进行稳健性检验，实证考察市场一体化对绿色发展效率的影响，具体的结果如下表8中第(1)-(3)列所示，从回归的结果可以看出，市场一体化对绿色发展效率的影响依然显著为正，充分说明基本回归结果稳健可靠。其次，我们参照李玉山和陆远权[49]的做法，构造一个排他性的安慰剂(Placebo)检验。即在使得本文选择的其他影响因素保持不变的情况下，人为地改变样本中市场一体化变量，如果市场一体化对绿色发展效率的促进效应仍不改变，则我们可以认为是本文观测样本中的某一未知因素，不仅强化了市场一体化对绿色发展效率的影响效果，而且对绿色发展效率产生了促进作用。因此，保持所有控制变量一一对应，将市场一体化随机分配给各城市，如果市场一体化对绿色发展效率的促进效应就此消失，我们即可认为是市场一体化本身而不是长三角城市群的其他因素影响了绿色发展效率。具体的结果如表8中第(4)-(6)列所示，此时的市场一体化对绿色发展效率未能产生显著性影响，这表明随机配对的市场一体化对绿色发展效率未能产生显著的影响，该结果与表基本回归结果形成鲜明的对比。因此，本小节借助安慰剂检验进一步排除了与市场一体化相关的其他因素对绿色发展效率产生促进作用的可能影响。

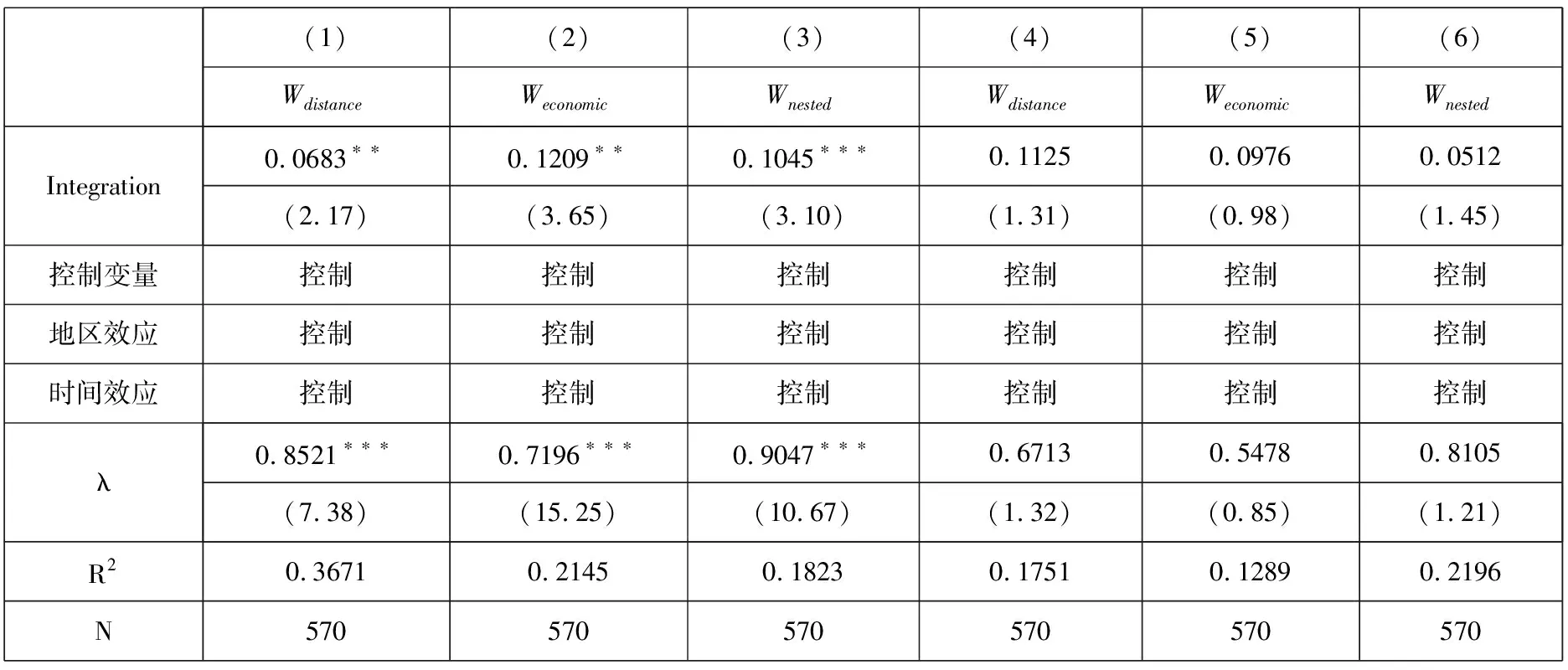
表8 稳健性检验

四、结论与政策建议

本文基于长三角城市群38个城市2004-2018年的面板数据，运用超效率SBM 模型对区域生态效率进行评价，并利用空间计量模型探讨了市场一体化对长三角城市群绿色发展效率的影响，得到以下结论：(1)总体来看，在2004年到2018年这一考察期内，长三角城市群大多数城市绿色发展效率水平值有了显著的提高，但是长三角城市群绿色发展效率呈现出非均衡的状态，各城市之间绿色发展效率水平存在较大差异，其中，长三角城市群省际间的差异是影响长三角城市群绿色发展效率总体区域差异的主要因素。(2)长三角城市群绿色发展效率呈现出显著的空间相关性，绿色发展效率水平相对较高的地区，其集聚空间溢出效应对周边区域也具有较强的辐射带动作用。实证结果还显示，长三角城市群绿色发展效率存在显著的正向空间交互效应。(3)从空间异质性来看，市场一体化对绿色发展效率的影响呈现出空间连片特征，上海、江苏与浙江三省(直辖市)回归系数普遍较高，上海、南京、苏州、扬州、杭州、温州、宁波以及合肥等城市，其中大多数城市经济比较发达，具有较大的系数。

根据以上的研究结论，本文提出如下政策建议：(1)加快推进长三角城市群市场一体化发展，适时清理长三角城市群内各城市存在的阻碍商品、资源、要素等跨区域流动的政策法规，消除市场壁垒，实行统一的市场规范，从而构建一个统一与全面开放的商品、要素市场；在要素资源配置过程中以价格机制为主导，以增强市场一体化在长三角城市群内对要素配置的作用，进一步促使长三角城市群产业结构转向清洁化并形成绿色发展体系。积极探索以市场化为导向的环境治理方法，提升金融市场对环境治理的作用，如积极开发碳金融、绿色信贷、绿色基金等新产品。(2)长三角城市群在促进城市绿色发展的过程中，应根据各城市经济发展水平与现有产业分布状况，实行适当的环境监管标准以满足不同企业的需求，从而推动城市群内各城市产业结构趋于合理化和高级化。加大财政投入以支持环境治理，加快淘汰污染产业和促进产业在城市群内有序转移；同时，增强城市群内各城市合作力度，避免由于产业结构变迁造成污染在产业链上下游间转移，充分发挥技术创新带来的溢出效应，使产业结构变迁能够在城市群内实现正向效应，进而推动长三角城市群绿色发展效率值的“高高”集聚。(3)长三角城市群逐步统一各地市政策法规，实现污染联防联治。建立统一的污染排放交易市场，提升污染排放交易权在城市群内跨区域配置效率，从而达到长三角城市群节能减排的目的。在城市群内实现跨区域污染核算，明确城市群内跨区域污染治理责任。长三角城市群各城市共同出资建立污染联防联治基金，根据各城市本身污染情况以及受外部污染程度来确定需要分摊的财政资金比重。长三角城市群在推动自身市场一体化的同时还应支持周边地区市场一体化的发展，在制定长三角城市群发展规划和其他政策时，应充分考虑对接周边地区相应的规划和政策，逐步消除市场分割对环境污染治理带来的负向影响。