种内竞争时滞对植被周期振荡模式的影响研究*

李 静， 孙桂全， 靳 祯

（1. 山西财经大学 应用数学学院， 太原 030006；2. 中北大学 理学院，太原 030051；3. 山西大学 复杂系统研究所， 太原 030006；4. 疾病防控的数学技术与大数据分析山西重点实验室， 太原 030006）

引 言

干旱地区约占地球陆地总面积的41%，与干旱地区人口占世界总人口比例(38%)相近.由于人为因素和气候变化，干旱和半干旱地区土地退化的面积预计将在未来几十年内急剧增加[1].植被作为这种脆弱生态系统的主体，其生长规律、空间分布模式以及生物量覆盖比例，可作为生态系统恶化和向好的早期指标[2-4].植被被称为生态系统工程师，不仅对物种和生境的丰富度有重要影响，还对生态环境的改善和维持具有重要作用[5].从2002 年初国家在西部地区开始启动退耕还林工程，到习总书记关于生态文明建设方面提出“绿水青山就是金山银山”的科学论断，进一步表明了对植被系统的研究变得更加必要和迫切.

植被的生存离不开水资源，土壤水分过低会抑制植被正常的生长发育.同时，植被的生长在一定程度上也会促进土壤水分分布结构发生变化.在干旱、半干旱地区，土壤水分已成为影响植被系统恢复和重建的主要限制因素.因而，利用数学动力学模型来研究植被与土壤水的作用机制引起了生态学家和数学家的广泛关注[6-12].1999 年，Klausmeier[6]首次利用反应扩散方程构建了一个包含植被和土壤水的动力学模型去解释非洲尼亚美附近地区植被形成的大尺度空间条纹状结构，发现这种空间分布模式主要是由土壤水的流动和植被对水资源的竞争导致的.Von Hardenberg 等[7]为了研究水资源有限地区的植物根系吸水而引起植被斑块对水的竞争作用，建立了一个在植被演化方程中考虑Holling-Ⅱ型的植被-土壤水反应扩散对流模型，解释了水资源有限地区观察到的点状、条状和带状分布模式产生的机制.Sun 等[11]解释了土壤水扩散强度的降低会导致植被斑图结构发生相变且经历间隙状、条状和点状分布结构，并且植被的增长依赖于反馈强度的临界值.

目前植被-土壤水模型的数学分析主要集中在空间分布模式形成理论的研究上，从而去解释自然界中各种植被空间分布结构的形成机制.事实上，自然界中还可观察到植被的生物量会随时间做周期振荡现象.例如，根据植被覆盖度1 公里的月数据发现甘肃省2010 年1 月至2018 年12 月植被覆盖度演变随年度推移呈现周期变化趋势(图1)，其中每一年的12 个柱体代表从1 月到12 月的植被覆盖度.然而，这种现象无法利用空间分布模式形成理论进行研究，需要寻求新的理论方法.因此，本文将从另一种理论角度出发去解释植被系统中存在的这类周期振荡现象.

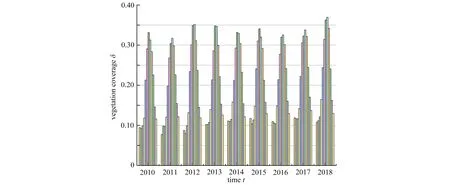
图1 从2010 年1 月到2018 年12 月甘肃省植被覆盖度随年变化的柱状图Fig. 1 Time series of vegetation coverages in Gansu Province from Jan., 2010 to Dec., 2018

本文考虑到植被的种内竞争存在于幼年期与成年期的植被之间，因此建立具有种内竞争时滞的植被-土壤水模型，从新的理论角度研究了植被随时间演化呈现周期振荡现象的内在演化机制.本文的内容结构安排如下：第1 节构建具有种内竞争时滞的植被-土壤水动力学模型；第2 节展示对应的常微分系统有植被灭绝平衡点和植被存在平衡点，并分析出系统在唯一的植被存在平衡点附近发生Hopf 分支的条件，给出相应的临界分支参数的表达式；第3 节基于数值模拟展示出系统在唯一的植被存在平衡点处产生了一族空间齐次的周期解，并发现种内竞争时滞影响空间周期振荡模式的发生，同时找到对临界分支参数、周期和振幅有显著影响的关键参数；第4 节对全文内容进行了总结和讨论.

1 动力学模型

不同于以往的经典植被模型[6]，文献[7]考虑到植被的饱和吸水效应提出了一个在植被方程中引入Holling-Ⅱ型作用项的植被-土壤水反应扩散对流模型：

其中，n(x,t)，w(x,t)分别为t时刻x位置的植被和土壤水的密度，参数γ表示植被对土壤水的吸收率， σ表示功能反应参数， µ表示植被的死亡速率，p表示降雨量，b表示蒸发率，d1，d2分别表示植被和土壤水的扩散率，∇2=∂2/∂x2表示一维空间上的Laplace 算子， β表示渗透层中植被根系引起的土壤水的扩散率.项γw/(1+σw)描述了植被的饱和吸水效应，−(1−bn)w表示土壤水的蒸发.利用数值模拟方法研究发现，模型产生了广泛分布在干旱和半干旱地区的点状、条状和带状空间分布模式.进一步预测了植被系统发生了从低降雨量的裸地态转变为高降雨量的均匀植被态的过程，其间产生不同的稳定状态共存现象.

接下来，我们将主要从动力学行为分析的角度对模型(2)进行研究.

2 动力学理论

2.1 平衡点及局部稳定性

不考虑时滞和空间时，模型(2)转变为如下的常微分系统：

表1 系统(3)正平衡点的存在情况Table 1 Existence properties of positive equilibrium points for system (3)

(Ⅰ) 当∆≤0时，由f(0)=α0>0和limw→+∞f(w)=−∞，易知三次函数f(w)和w轴之间仅有一个位于w右半轴的交点(见图2(a))，则f(w)=0有唯一一个正实数根w∗>0.因此，系统(3)有一个唯一的正平衡点E∗=(n∗,w∗).

图2 方程(4)存在唯一正实数根的示意图：(a) 情形(Ⅰ)；(b) 情形(Ⅱ)(i)；(c) 情形(Ⅱ)(ii)(其中红色实心点代表正实数根，图(a)中亮蓝色和蓝色曲线分别表示∆=0和∆<0的情形)Fig. 2 Schematic diagrams of the existence of the unique positive real root for eq. (4): (a) case (Ⅰ); (b) case (Ⅱ)(i); (c) case (Ⅱ)(ii), where the red dot represents the positive real root, the light blue and the blue curves of fig. (a) represent the cases of ∆=0 and ∆<0, respectively

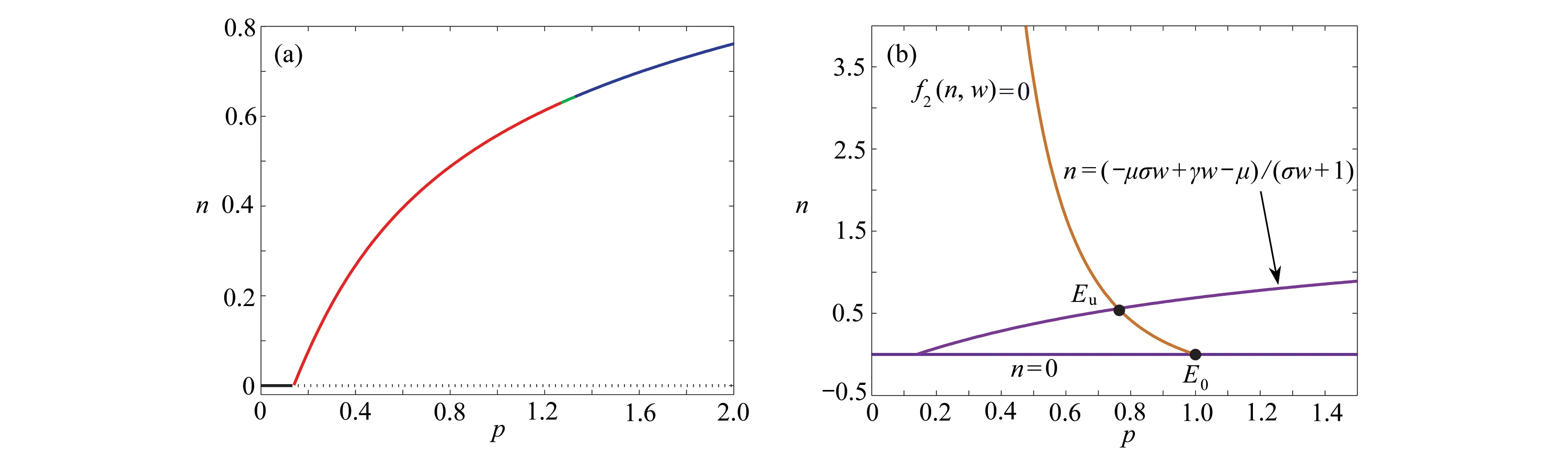
图3 平衡点的存在情况和零斜率线图： (a) 植被生物量n随着参数 p的变化；(b) 在w-n 平面上零斜率线f1(n,w)=0(紫色/洋红色)和f2(n,w)=0(橘色)形成的交点(黑色实心点)，其中 E0 和E u表示植被灭绝平衡点和植被生存平衡点，参数γ=1.6，σ=0.8 ，µ=0.2，b=0.2Fig. 3 The existence of equilibria and zero-slope diagrams: (a) vegetation biomass n vs. p; (b) the intersection (black solid points) formed by zero-slope line f1(n,w)=0 (purple/magenta) and f2(n,w)=0 (orange) on w-n plane, where E0 and Eu are the vegetation extinction equilibrium points and the vegetation existence equilibrium points, γ=1.6，σ=0.8 ，µ=0.2，b=0.2

通过计算，可推出系统(3)在植被灭绝平衡点E0=(0,p)处的Jacobi 矩阵为

对应的特征方程为

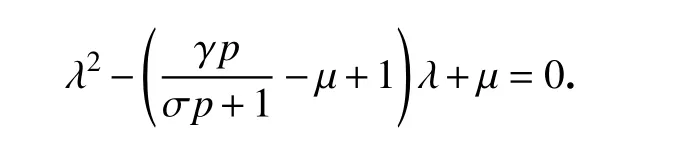
容易得到特征值为λ1=−1和λ2=γp/(σp+1)−µ.若条件

2.2 非空间系统(2)的动力学行为

通过以上的分析可得到如下结论.

定理1 如果条件(C2)成立，

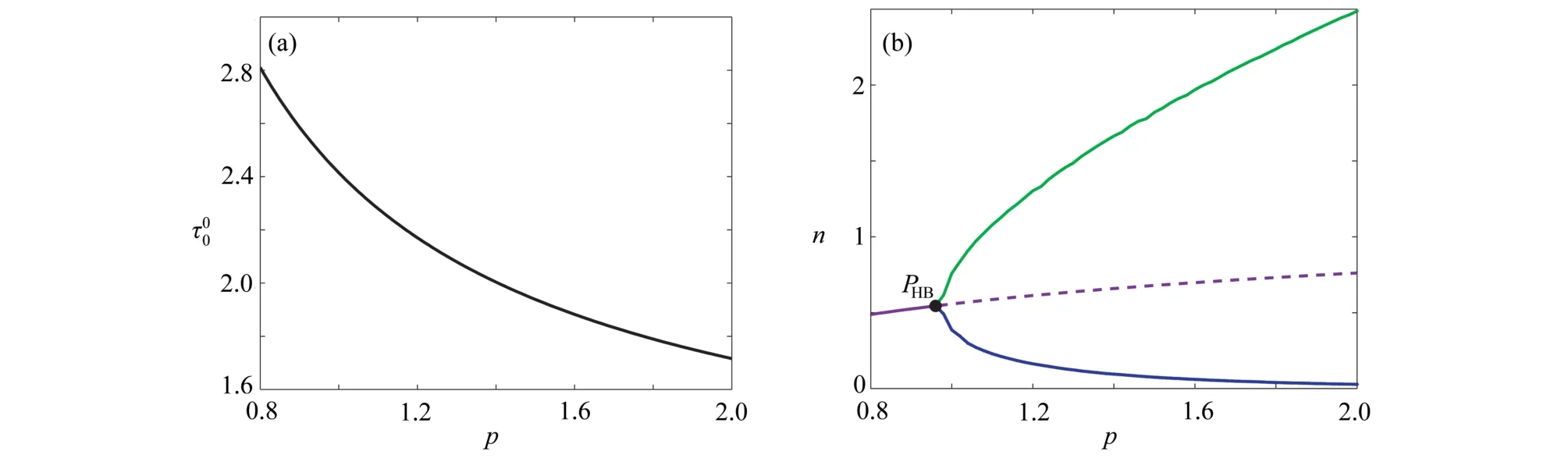
图4 临界时滞 τ00和植被生物量随参数p 的变化情况： (a) τ00随参数 p的变化情况；(b) (p,n)平面上的单参数分支图，参数σ=0.8，µ=0.2，b=0.2，γ=1.6 ，τ=3Fig. 4 The changes of the critical delay τ00 and the vegetation biomass with parameter p: (a) the variation of τ00 with p; (b) bifurcation diagram in (p,n) plane for σ=0.8 , µ=0.2, b=0.2 , γ=1.6 and τ=3

2.3 系统(2)的动力学行为

当系统(2)不考虑时滞时，即k≠0和τ=0，对应的特征方程为

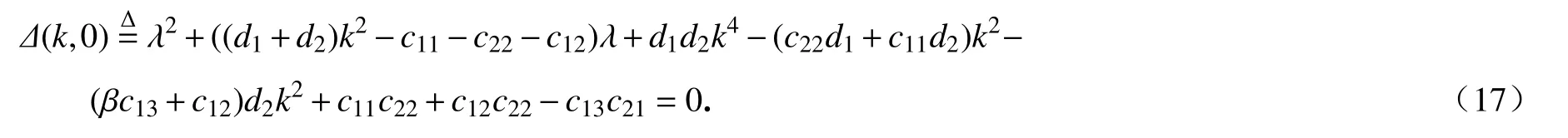
可以计算出

根据以上的分析内容，可获得下述的结果：

定理2 如果条件(C3)和(C4)同时成立，则

定理1 和2 的结果说明非空间和空间植被系统均可发生植被随时间演化呈现周期振荡模式的现象.

3 数 值 模 拟

这一节通过对系统(2)在一维空间上执行一系列的数值模拟去验证第2 节的理论结果.此外，进一步细致分析系统参数对临界时滞值、周期振荡模式的周期和振幅的影响程度.

3.1 非空间系统(2)的动力学行为

本小节通过数值模拟验证定理1 的理论结果，并研究降雨量p对临界时滞值 τ00、周期震荡模式的周期和振幅的影响.主要关注非空间系统(2)发生Hopf 分支的行为，因此假设d1=d2=β=0.选择参数σ=0.8， µ=0.2，b=0.2，γ=1.6，p=1.0，计算出Eu=(0.557,0.762)， τ00=2.41. 当τ=1<τ00时，图5(a)展示了非空间系统(2)的解最终趋于唯一的植被存在平衡点Eu，表明Eu是局部渐近稳定的；当τ=3>τ00时，图5(b)展示了植被生物量和土壤水的密度随时间演化呈周期振荡现象，表明非空间系统(2)在Eu处产生了一族周期解，并通过相图(c)呈现极限环(蓝色线和红色点分别代表轨线和Eu).

图5 非空间系统(2)解的数值模拟： (a) τ=1；(b) τ=3；(c) 相图Fig. 5 Numerical simulation of the solution of non-spatial system (2): (a) τ=1; (b) τ=3; (c) the phase diagram

图6 展示了临界时滞 τ00随着参数γ，b和 σ的变化情况.从图6(a)可观察到 τ00随着参数γ的增加而快速减少，表明了植被对土壤水的吸收速率强度变大有利于植被与土壤水以周期振荡的形式共存.从图6(b)中观察到τ00随着参数b的增加而缓慢减少，说明蒸发率的增加会促进这种共存作用形式，但这种促进作用相比于土壤水的吸收速率是缓慢的.图6(c)展示了 τ00随着参数 σ增加而变大，反映了功能反应强度的增加反而抑制这种周期振荡行为.同时，3 个图一致呈现出 τ00随着降雨量的增加而减小，这一结果说明降雨量与植被土壤水的吸收速率和蒸发率的效应一样.

图6 对于p=1.0,1.3,1.6 ，τ 00随着γ , b, σ 的变化情况，其他参数为σ=0.8 ，µ=0.2，b=0.2 ，γ=1.6Fig. 6 The variations of τ 00 with γ , b, σ for p=1.0,1.3,1.6, with other parameters of σ=0.8 , µ=0.2, b=0.2, γ=1.6

3.2 空间系统(2)的动力学行为

本小节将通过数值模拟验证定理2 的理论结果，主要关注降雨量参数p对临界时滞、齐次空间周期振荡模式的周期和振幅的影响.选取参数σ=0.8， µ=0.2，b=0.2， γ=1.6，p=1.0，d1=0.02，d2=0.2， β=2.计算出常数稳态解Eu=(0.557,0.762)，=4.64.当τ=1<时，图7(a)展示了空间系统(2)的解最终趋于唯一的稳态解Eu，表明Eu是局部渐近稳定的.当τ=4.8>τ02时，图7(b)、(c)展示了空间系统(2)的解最终趋于空间齐次的周期解，表明稳态解Eu失去稳定性，即从Eu处分支出一族渐进稳定的空间齐次周期解.为了更清晰地展示出周期振荡行为，从图7(b)中截取时间1200～1400 部分作为图7(c)，通过将图7(c)投影到时间和空间坐标面形成图7(d)，呈现一种时空周期行为.

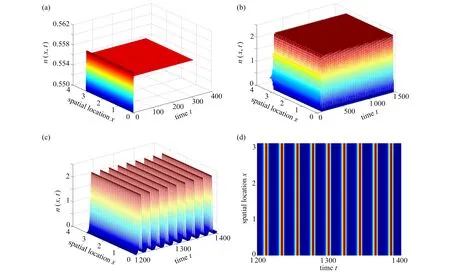
图7 n(x,t)的时空演化图：(a) τ=1；(b) τ=4.8；(c) 截取图(b)形成的部分图；(d) 图(c)的二维时空图Fig. 7 The time series of n(x,t): (a) τ=1; (b) τ=4.8; (c) the partial graph cut out of fig. (b); (d) the 2D spatiotemporal graph of fig. (c)

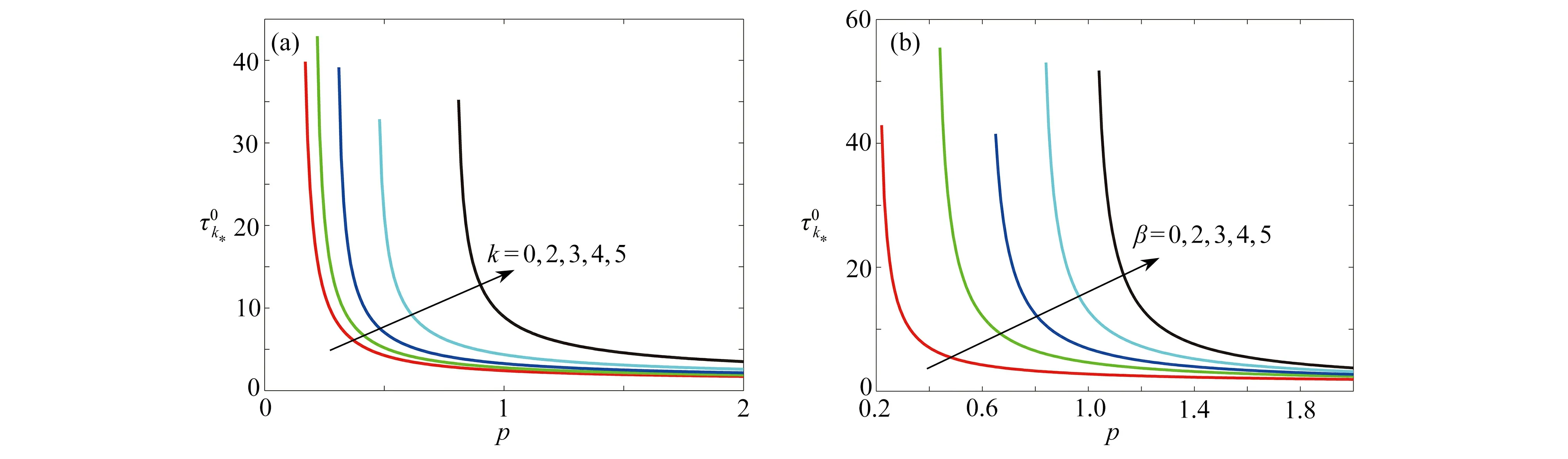
图8 对于不同的k和β，随着参数p的变化Fig. 8 The variations of with p for different k and β values

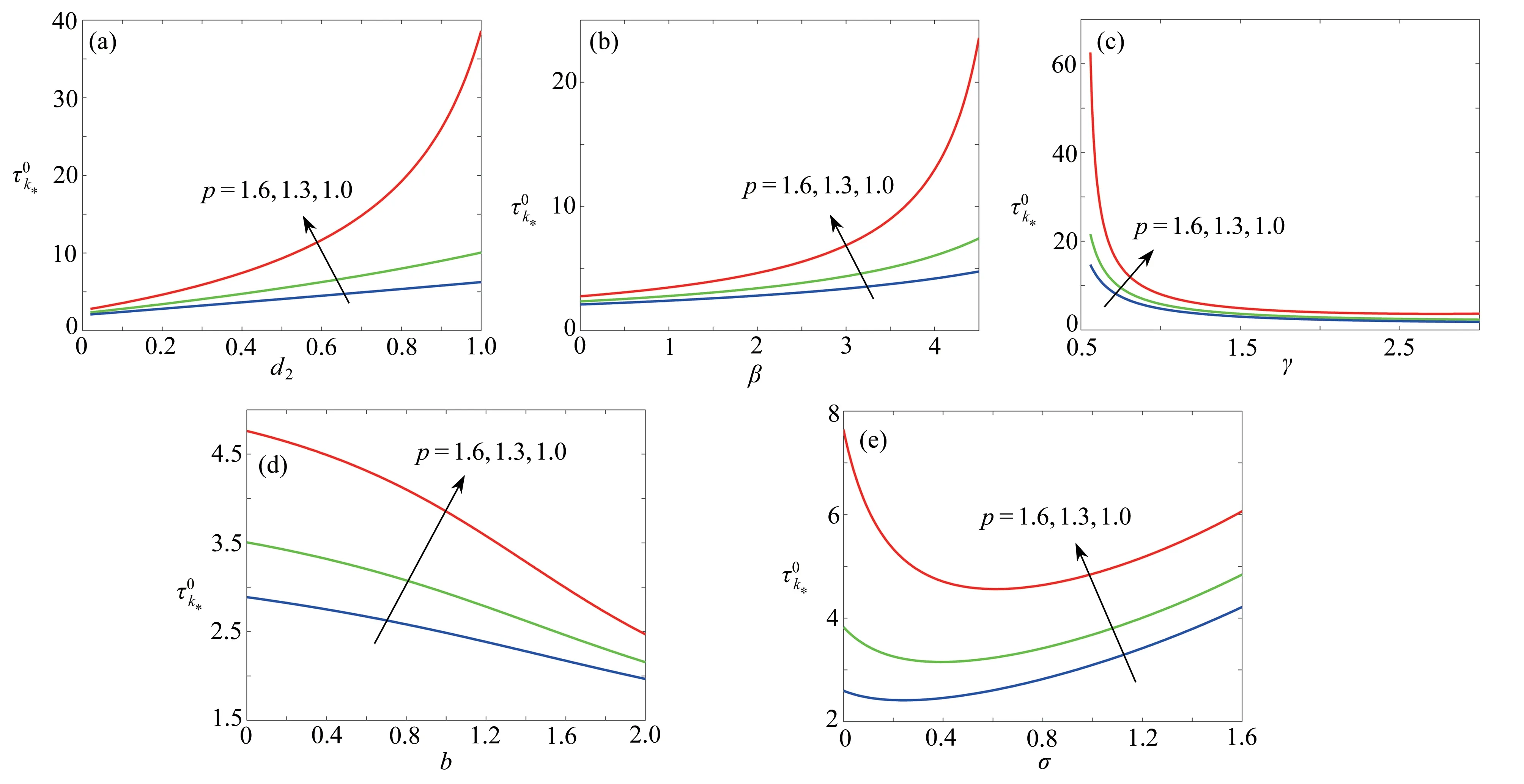
图9 对于不同的参数 p ，随着d 2，β ，γ ，b ，σ 的变化情况Fig. 9 The variations of with d 2, β , γ , b, σ for different p values

3.1 和3.2 小节的数值模拟结果已表明在特定的参数取值下非空间系统和空间系统都能发生周期振荡模式.为了研究参数取值变化能否保持这种模式，以及辨识出临界时滞值、周期振荡模式的振幅和周期对参数变化的敏感性程度，我们将对两种系统作参数局部敏感性分析[16]，其中局部敏感性系数(Slocal)的计算公式为

这里，Vpar表示两个系统中参数的值，∆par是对参数值做两个方向的微小扰动(+/−10%)，VNR和∆NR分别对应于Vpar 和∆par的数值模拟结果，如τ00/τ02、振幅和周期的模拟结果.为了评估参数的影响程度，作以下规定：敏感性系数大于2 时，此参数为高敏感参数；敏感性系数介于1 和2 之间为中度敏感参数，否则为低敏感参数.

在图10 中，第一行和第二行分别描述了非空间系统和空间系统对应的τ00/τ02、振幅和周期对每个参数的敏感性程度，可以看出参数γ始终是高敏感参数而b是低敏感性参数，表明植被对土壤水的吸收率对植被系统的震荡模式影响最显著，但系统对参数b的 鲁棒性最强.从图10(a)、(c)、(d)和(f)中可观察到 σ 和µ对 τc和周期来说是低敏感参数，但对于振幅来说是中度敏感性参数.此外，由图10(d)～(f)可知， τ02受土壤水的扩散速率d2和植被根系引起的土壤水的扩散速率β的影响较大，而受植被的扩散速率d1的影响小，但这三个参数对振幅和周期没有任何影响，表明空间扩散因素会影响周期振荡模式的发生.此外，降雨量p的影响比较复杂，对 τ02、非空间周期、空间振幅是中度敏感性参数，对非空间振幅是高敏感参数，对 τ00、空间周期是低敏感参数.

图10 周期振荡模式的敏感性分析，参数σ=0.8 ，µ=0.2，b=0.2 ，γ=1.6 ，d1=0.02 ，d2=0.2，β=2，k=2Fig. 10 Sensitivity analysis of periodic oscillation patterns with parameters of σ=0.8 , µ=0.2, b=0.2 , γ=1.6, d1=0.02, d2=0.2, β=2, k=2

4 结论和讨论

考虑到干旱、半干旱地区的幼年植被与成年植被之间存在竞争土壤水资源的现象，本文构建了一个具有种内竞争时滞的植被-土壤水动力学模型.利用动力系统理论分析出对应的常微分系统存在一个植被灭绝平衡点E0，并给出唯一植被存在平衡点出现的判定条件.随后给出非空间系统在唯一的植被存在平衡点Eu处发生Hopf 分支的条件并计算出独立于空间扩散的临界时滞值(j=1,2,···).同时可计算出依赖于空间扩散的临界时滞值，发现当时滞值大于依赖于空间扩散的临界时滞时，原来考虑空间扩散的系统在Eu处可以产生空间齐次的Hopf 分支周期解.数值模拟进一步验证了植被随时间的推移呈现周期振荡模式，为解释干旱、半干旱地区植被生物量的周期振荡演化提供了新的理论视角，也可以为干旱、半干旱地区植被系统的保护和治理提供理论依据.

本文研究发现，降雨量、植被土壤水的吸收速率强度和蒸发率的增强均有利于非空间植被周期振荡模式的发生，但植被与土壤水的功能反应强度的加大反而会产生抑制效应.另外，对具有空间扩散的系统，波数和植被根系引起的土壤水的扩散反而会抑制这种行为，表明了空间因素的引入使得植被系统不易发生周期振荡模式现象，同时空间扩散的引入会影响其他参数对这种模式的影响.相比于无空间因素，影响效果会变得复杂.通过参数敏感性分析发现非空间参数均对和产生影响，但敏感性程度不一致，同时降雨量和植被的增长率影响尤为显著；系统的非空间参数均可对非空间和空间振荡模式的周期产生相同的影响效果，特别是植被增长率 γ和降雨量参数p的影响显著；空间因素对依赖于空间的临界时滞参数 τ00有影响，敏感性程度为β>d2>d1，但对空间齐次振荡模式的周期和振幅没有影响.文中利用Hopf 分支理论研究干旱、半干旱地区植被生物量随时间演化做周期振荡模式的内在机制，但未结合实际的干旱、半干旱地区的植被生物量数据进行讨论，在后续工作中我们将对具体地区的植被展开相关的周期振荡模式研究[17-18]，进而因地制宜地给出影响植被生物量的关键因素.

参考文献（ References ） ：

［1］E IGENTLER L, SHERRATT J A. Metastability as a coexistence mechanism in a model for dryland vegetation patterns[J].Bulletin of Mathematical Biology, 2019, 81（7）: 2290-2322.

［2］P RINGLE R M, DOAK D F, BRODY A K, et al. Spatial pattern enhances ecosystem functioning in an African savanna[J].PLoS Biology, 2010, 8（5）: e1000377.

［3］G OWDA K, CHEN Y, IAMS S, et al. Assessing the robustness of spatial pattern sequences in a dryland vegetation model[J].Proceedings of the Royal Society A, 2016, 472: 20150893.

［4］G ETZIN S, YIZHAQ H, BELL B, et al. Discovery of fairy circles in Australia supports self-organization theory[J].Proceedings of the National Academy of Sciences of the United States of America, 2016, 113（13）:3551-3556.

［5］G ILAD E, VON HARDENBERG J, PROVEBZALE A, et al. Ecosystem engineers: from pattern formation to habit creation[J].Physical Review Letters, 2004, 93（9）: 098105.

［6］K LAUSMEIER C A. Regular and irregular patterns in semiarid vegetation[J].Science, 1999, 284（5421）: 1826-1828.

［7］V ON HARDENBERG J, MERON E, SHACHAK M, et al. Diversity of vegetation patterns and desertification[J].Physical Review Letters, 2001, 87（19）: 198101.

［8］L IU Q X, JIN Z, LI B L. Numerical investigation of spatial pattern in a vegetation model with feedback function[J].Journal of Theoretical Biology, 2008, 254（2）: 350-360.

［9］B ONACHELA J A, PRINGLE R M, SHEFFER E, et al. Termite mounds can increase the robustness of dryland ecosystems to climatic change[J].Science, 2015, 347（6222）: 651-655.

［10］T ARNITA C E, BONACHEL J A, SHEFFER E, et al. A theoretical foundation for multi-scale regular vegetation patterns[J].Nature, 2017, 541（7637）: 398-401.

［11］S UN G Q, WANG C H, CHANG L L, et al. Effects of feedback regulation on vegetation patterns in semi-arid environments[J].Applied Mathematical Modelling, 2018, 61: 200-215.

［12］L I J, SUN G Q, JIN Z. Interaction of time delay and spatial diffusion induce the periodic oscillation of the vegetation system[J].Discrete and Continuous Dynamical Systems(Series B), 2022, 27（4）: 2147-2172.

［13］曹 建智, 谭军, 王培光. 一类具有时滞的云杉蚜虫种群模型的Hopf分岔分析[J]. 应用数学和力学, 2019, 40（3）: 332-342. （CAO Jianzhi, TAN Jun, WANG Peiguang. Hopf bifurcation analysis of a model for spruce budworm populations with delays[J].Applied Mathematics and Mechanics, 2019, 40（3）: 332-342.（in Chinese））

［14］谷 雨萌, 黄明迪. 一类时间周期的时滞竞争系统行波解的存在性[J]. 应用数学和力学, 2020, 41（6）: 658-668. （GU Yumeng, HUANG Mingdi. Existence of periodic traveling waves for time-periodic Lotka-Volterra competition systems with delay[J].Applied Mathematics and Mechanics, 2020, 41（6）: 658-668.（in Chinese））

［15］欧 阳颀. 非线性科学与斑图动力学导论[M]. 北京: 北京大学出版社, 2010. （OUYANG Qi.Introduction to Nonlinear Science and Pattern Dynamics[M]. Beijing: Peking University Press, 2010. （in Chinese））

［16］I NGALLS B. Sensitivity analysis: from model parameters to system behaviour[J].Essays in Biochemistry, 2008,45: 177-194.

［17］K ÉFI S, RIETKERK M, ALADOS C L, et al. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems[J].Nature, 2007, 449（7159）: 213-217.

［18］B ASTIAANSEN R, JAÏBI O, DEBLAUWE V, et al. Multistability of model and real dryland ecosystems through spatial self-organization[J].Proceedings of the National Academy of Sciences, 2018, 115（44）: 11256-11261.