数的进位制符号

徐品方

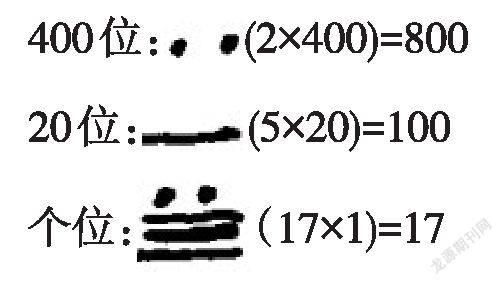
在文字产生以前，人类已经形成数的概念，用实物，如石子、竹片、贝壳等计数，有时也用手指和脚趾来计数，后来使用了结绳法和契刻法.随着数目的增大，人类开始使用进位制.由于各地区、各民族所处的自然环境与社会环境都不相同，因此出现了各种不同的记数方法和记数符号.

（1）5进位制.一只手有5个手指，表示数“5”.5进制以罗马数字为代表，如1、2、3、4的符号是I、II、III、IIII，5的符号不是IIIII，而是V;6、7、8、9的符号分别是VI、VII、VIII、VIIII，10的符号是X，这就是5进制数码的雏形.直到1800年，德国农民日历上的数字符号还是5进制的.至今，南美洲的玻利维亚群岛的居民还在使用5进制符号.

（2）10进位制.10进制是最常用的一种记数法，即以10为进位基数的位值制记数法.十进制的基数为10，数码由0-9组成，计数规律是逢10进1.因为每个人都有10个指头，所以用10来计数最为方便.

在公元前2000年的埃及与公元前1600年的中国（商朝），就已经出现了10进位制记数法，并且在中国还出现了一、十、百、万等文字符号.1971年8月在陕西千阳县的一座西汉墓中，首次出土了骨质算筹.估计算筹的使用不会晚于公元前3世纪.用算籌表示数有纵横两种方法：

用算筹摆数的原则在《孙子算经》中有记载：“凡算之法，先识其位，一纵十横，百位千僵，千十相望，万百相当.”意思是，个位、百位、万位都是纵式;十位、千位都用横式，高位在左，低位在右，遇到0时，就留个空位.”

这里需要特别指出的是，中国的10进制数中数字的位置不同表示的数也不相同.如43和74这两个数中都含有数字4，43中的4在十位上表示40，而74中的4在个位上表示4.古埃及人发现的10进制虽说是世界上最早的，但它采用的是累计制，而不是位值制.公元595年，人们在印度人的碑文上发现了10进位值制符号，比我国晚了一千年.

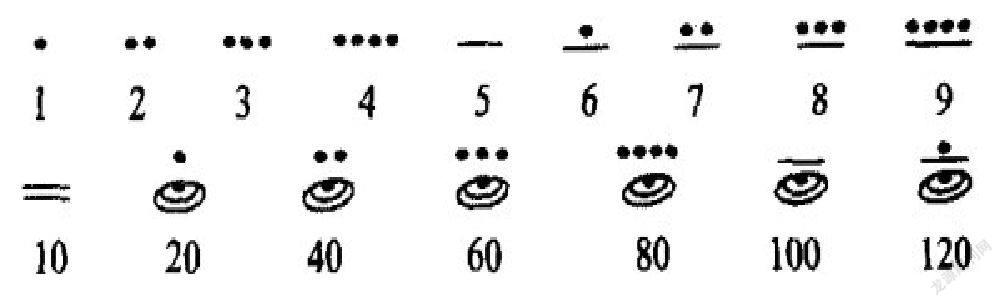
（3）20进位制.玛雅人最先使用20进制来计数.玛雅地处热带，人们喜欢打赤脚，记数时手指不够，就用脚趾，于是产生了20进制.玛雅人早期使用的数字有：

后来又使用另一套记数系统，1～4用小点表示，满五个，将“·”改为一横“-”或竖“丨”;6～9用一横点数（或一竖左边点数，如7表为“：丨”）表示;11～14用两横“=”或竖表示.如13表为“丨鼠”;16～19用三横（竖）表示，满20进1位，故为20进位.数1-19用如下符号表示.

玛雅和巴比伦的记数法有相似之处，20以下用5进位的简单累数制，20以上用位值制.这套数码中还

玛雅人在一般的计算中，用严格的20进位制，表示任何一个非负整数，以便进行加减运算.把单位数字的符号由下向上堆积起来，即一个多位数要分层书写，高位在上，低位在下，只写每一位的倍数，由低位向高位依次写出，满20则进1位.例如，10进制的数917，用20进制表示为如下三层：

即用2个400，5个20，17个1组成.

（4）12进位制.12进位制的起源之说有很多种.有的说，可能与人的一只手的关节有关.除大拇指外，其余4个手指有12个关节;又有的说，可能是与一年有12个月有关;还有的说，12是所有两位的“多倍数”中最小的一个，除1和12外，它还有约数2、3、4、6，12虽然比10只大2，但约数却比10的约数多2个，用它作除数整除的机会就多.现今留下来的计数方法中仍有12进制，如1罗=12打，1打=12个，1呎=12时，1先令= 12便士等.

（5）16进位制.16进位制大多应用于实际生活中. 如中国古时1斤=16两，1俄尺=16俄寸，1磅=16英两.

由于16=2，它与2的关系十分密切，所以在电子计算机方面，常被用作10进制与2进制的一种过渡进位制.16进制数有两个特点：它有16个数码，即由数字0～9加上字母A-F组成（它们分别表示十进制数10～15），16进制数的运算规律是逢16进1，即基数为16，通常在数的尾部标H或下标16以示区别，在C语言中添加前缀0x以表示16进制数.例如：16进制数4AC8可写成（4AC8）16，或写成4AC8H.

（6）60进位制.60进位制是地处亚洲西部的巴比伦（今伊拉克境内）人于公元前2000年前首先创制的.60进制的起源有几种说法.有的说，60是2、3、4、5、6、10、12、15、20、30、60的倍数，可使计算简化;有的说，与圆周分成360份有关.关于60进制的起源之说较多，至今还没有一致的看法.流传至今的60进制有：1小时=60分，1分=60秒，圆周角=360度，1度=60分，1 分=60秒等.

（7）2进位制.可以说，我国最早应用2进制计数.公元前11世纪的古书《周易》（即易经）中记载：“易有太极，是生两仪，两仪生四象，四象生八卦”，意思是说，一分为二，二分为四，四分为八.用现代数学式子表示，可写成2=1、2=2、2=4、2=8.

介于澳大利亚北部的约克角半岛与伊利安之间的托列斯海峡的附近群岛上居住着一些部落.他们是靠两个数“一”（叫乌拉勃）和“二”（叫阿柯扎）进行计算的.遇到“三”就用“阿柯扎、乌拉勃”表示，“四”是“阿柯扎、阿柯扎”，“五”是“阿柯扎、阿柯扎、乌拉勃”，他们使用的是2进制，并用文字来表示.

（8）8进位制.8进制依据“逢8进1”的法则，使用0，1，2，3，4，5，6，7八个数字来记数.由于在电子计算中，用2进制记数数位较多，使用起来不方便，在编写计算机解题程序时，常常需使用8进制.

任何一个8进制的数，可以写成底数为8的幂的和的形式.这样很容易将其化为10进数，如8进制数205=2×8+0×8+5×8=133.反之，一个10进制的数只要用底数8连续去除，反序取全数，就可以得到8进制数.

虽然，数的进位制有很多种，但据调查，世界上大多数地区还是采用10进位制来计数.1920年前后，美国科学家易勒斯（W.C.Eels）曾做过调查，美国原始亚美利加各族的307种计数系统中，有146种是10进制的，有106种是5进制或20进制的.

综上所述，在世界上的不同年代，出现了五花八门的进位制和令人眼花缭乱的记数符号系统，都足以证明数学符号的多元性和多样化.

——摘自《数学符号史》