一种无电解电容的新型削峰填谷电路∗
曹 冰刘 伟
(河南省高速铁路运营维护工程研究中心 河南 郑州 450000)
环境问题日趋严重,高亮度LED 由于其能耗低等优点已广泛应用于照明领域。然而,LED 只能直流驱动;因此,LED 驱动系统中必须加入AC-DC 变换器。两级及以上AC-DC 变换器,通常前级作为功率因数校正(Power Factor Correction,PFC),后级作直流变换[1]。此类变换器具有良好的功率因数特性和低纹波输出,但能量多级变换功耗高。相比之下,单级AC-DC 变换器更适用于低功耗场合。为了实现自动PFC,变换器在前级工作于非连续导通模式(Discontinuous Conduction Mode,DCM),一般只适用于低功耗场合。
在中等功率应用场合下,相比于DCM 反激变换器,前级Boost 变换器工作于连续导通模式时具有更好的经济性。特别是当二次侧工作在连续导电模式(Continuous Conduction Mode,CCM)下,变换器拥有较小的变压器铁芯[2-5]。但这种拓扑只用于理论研究,在工程上难以发挥作用。第一,由于PFC 和DCDC 变换电路不可避免的相互作用,电路的关键参数难以确定。第二,轻载时储能电容和高频开关的电压应力数倍于额定负载,并且电压应力的问题在宽范围交流输入时会变得更加严重。
对此,采取PWM 调光使变换器的工作状态只切换于空载和额定负载之间,因此,储能电容的电压应力只决定于额定负载情况。因此,文献[6-7]采用双PWM(DPWM)控制策略用于调整平均输出电流。
在电力变换器中,通常采用两阶削峰填谷电路以减少器件数量。此类拓扑应用分为两类,一类主要用于被动PFC 和减少两倍工频的脉动电压[8-14]。其中,高阶填谷电路在功率因数校正和总电流谐波畸变率(Total Harmonic Current Distortion,THD)的表现更佳[9-10]。文章[13]对已有削峰填谷电路加以改进,提出一种填谷电路复用变压器线圈的方式减少主开关器件的电压应力,但在电压峰值输入下,开关管最大占空比限定在1/3。文章[14]利用变压器部分线圈钳位填谷电路的电容电压。该方法能够实现输入电流导通角度的设置,可实现最优的功率因数。第二类填谷电路一般用高频开关来替代储存电容,可以获得较低的输出纹波和电压应力[15-18]。文献[16]利用两个额外增添的开关器件使填谷电路参与谐振,避免了输入电流的死区。然而,等效直流量和占空比大范围变化,磁性器件难以优化。为此,实践中解决此类问题通常在整流后嵌入一个选择开关和一个电压倍增模块,但是低压输入下的电压应力仍然会倍增,严重影响传递效率。
基于上述考虑,本文提出了一种新型削峰填谷式无电解电容单级LED 驱动器,相比于倍增电压的方案,本文设计的驱动器有两个主要优势。其一,低电压输入下有较低的电压应力;其二,减小了开关管、储存电容和二极管的电压应力。简而言之,本文主要包括电路的设计分析和设计原则,尤其是填谷电路的电容选型。
1 填谷电路的工作原理
本文所提结构如图1 所示。填谷电路由三个二极管D3,D4,D5和两个电容C1,C2组成,两个电容表现为串联充电和并联放电的特性,填谷电路通过和C2并联一个范围选择开关S1来实现,并连接于变压器Tf的绕组N1。S1手动操作,在90 V~135 V内关闭,在180 V~265 V 内打开,以达到宽线电压范围内更好的性能。
S1处于关断状态时,C2短路,二极管D6反向截止。C1充或放电,D3和D4均为导通状态。如忽略二极管的导通压降,本文拓扑与传统的单级三绕组磁通平衡升压正激变换器相比,得到改进;其工作模态简要分析如下:当S2导通时,L1由Vrec充电,C1通过Tf向L2和负载放电;当S2关断时,C1通过Vrec和L1充电,N1开始通过D6向C1放电,同时L2向负载放电,仅L2的放电过程持续到下一个开关周期开始。
S1处于导通状态时,传统前级Boost 变换器的储存电容被填谷电路替代,N1通过D4和D6同C1相连。一个开关周期的电路模态分为四部分,每一部分的等效电路和关键波形分别如图2 和图3 所示。Vrec是整流后的交流输入电压,VC1G为C1两端电压,Vbus为C1上平均电压的两倍。
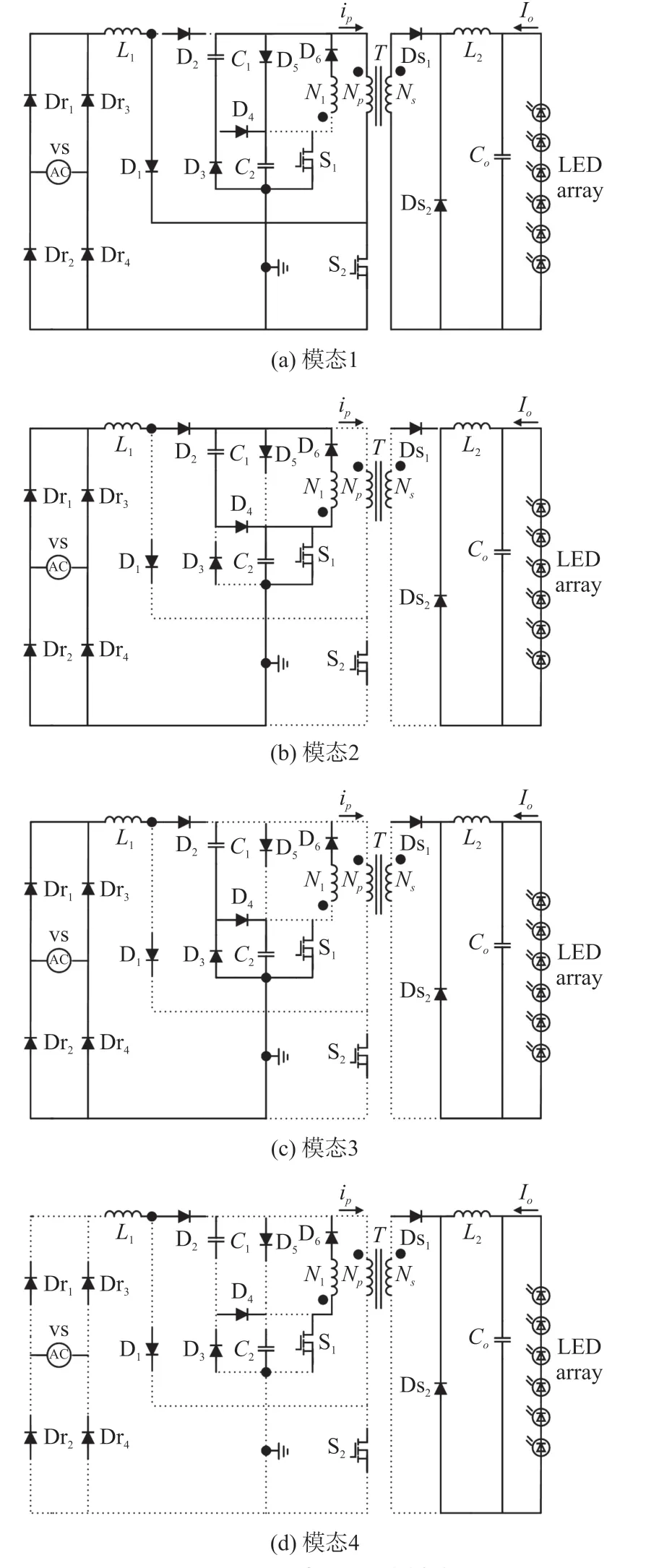
图2 所提电路拓扑模态
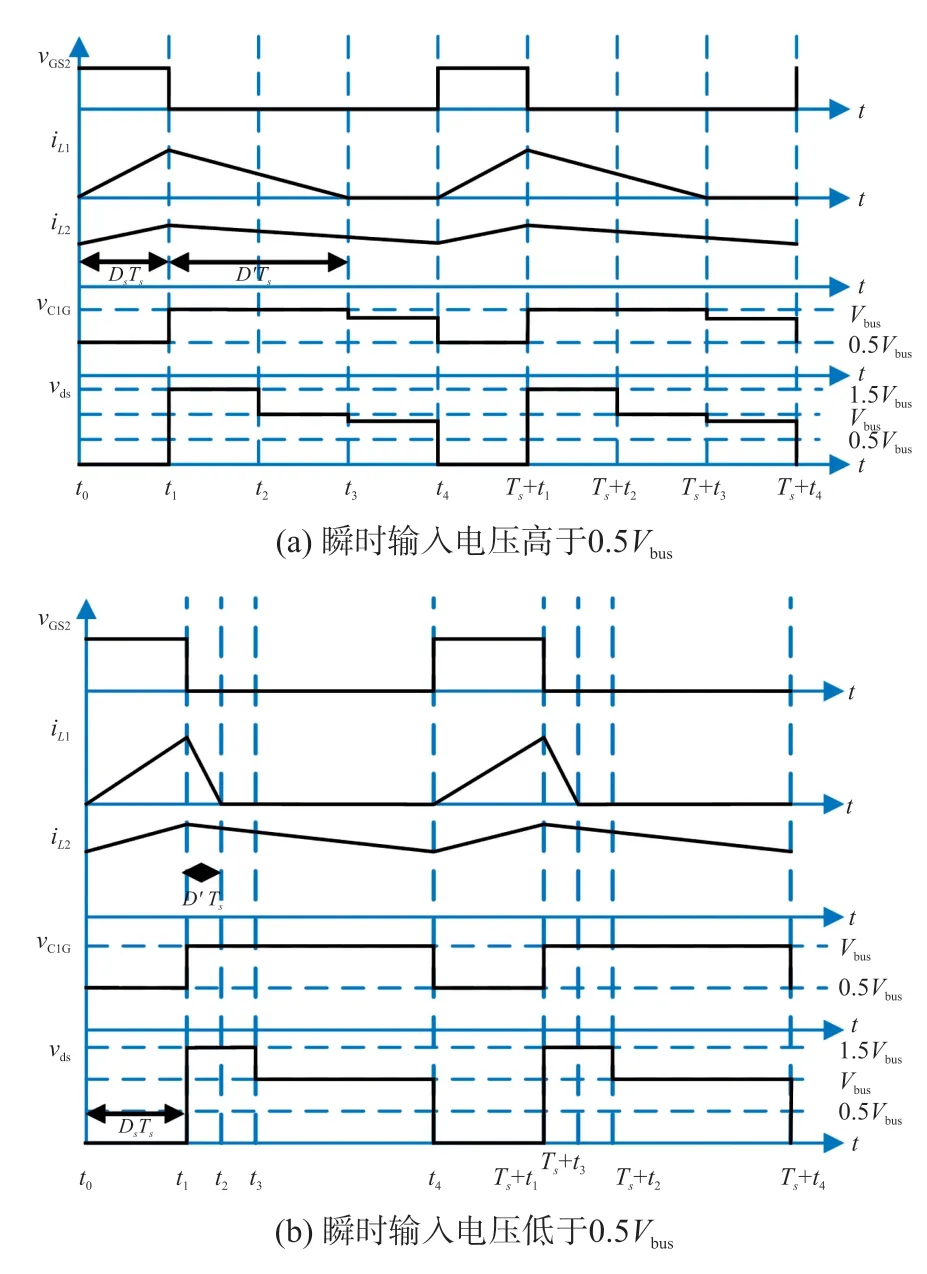
图3 所提电路在一个开关周期内的理论波形
模态1[t0,t1]假设L1的初始电流为零,当S2在t0时刻导通时,形成两个电流环路;第一个是L1由正弦输入电压充电,第二个是填谷电路中C1和C2对Tf充电,因此Tf的前级电压是0.5Vbus,VC1G为0.5Vbus。S2关断,此模态结束。在过程中,iL1线性递增,iL1的峰值可以近似等效于公式(1)。

式中:Ds是开关S2的占空比,Ts是变换器的开关周期。
Tf的原边侧平均电流定义为公式(2)。

式中:Lm是Tf的前级电感,Ntf=Np/Ns为Tf的匝比。相比之下,传统前级Boost 变换器关系如下所示:
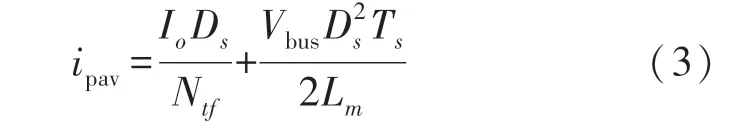
模态2[t1,t2]当S2关断时,变换器状态做如下改变:
(1)填谷电路的工作状态从并联放电切换到串联充电,C1和C2串接且吸收L1和vin输出的能量,因此,此工作模态下VC1G=Vbus;
(2)L2开始向输出放电直至本模态结束;
(3)N1通过D4和D6向C1充电,储存在变压器铁芯内的能量被回收到C1,铁芯在t2达到磁通平衡。Vds=Vbus+VC1=1.5Vbus。
因此,磁化和退磁过程中的铁芯电压都是Vbus的一半,根据磁通平衡原理,当Np=N1时,稳定状态下的最大占空比不会超过50%。
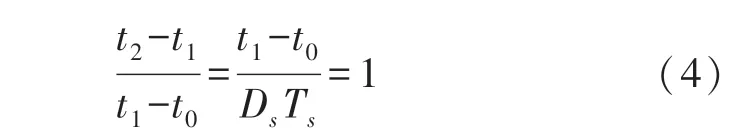
模态3[t2,t3]L1持续向填谷电路充电,直到iL1降为零,该模态下由于变压器线圈无电压,Vds降低到Vbus,假设D′为iinpk相应的占空比,则:

D′可由下式获得。
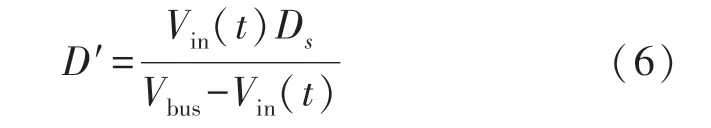
模态4[t3,t4]在此模态,前级器件全部断开,L2持续放电,直到S2再次导通,下一个切换周期重新开始。假设Vo为输出电压,由于后级工作于连续电流模式(CCM),根据L2的伏秒平衡,得:

然而,传统的变换器满足公式(8)。

从图1 中,C1和C2在D′Ts间隔由电流iin充电,在DsTs内放电。根据充放电平衡应等效,可得:
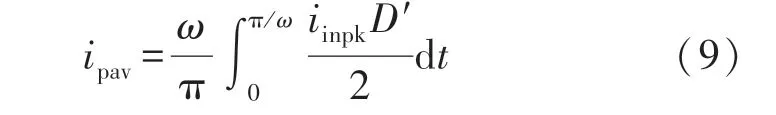
将式(1)、式(2)、式(6)和式(7)代入式(9)或者将式(1)、式(3)、式(6)和式(8)代入式(9),均可得:

观察式(6),D′随Vin(t)变化,如果D′=Ds则临界电压可以求解。同时结合式(4)和式(5),可得Vin(t)=0.5Vbus和t2=t3。当连续交流输入高于0.5Vbus时,t3>t2,得以保障,且时序与图2 相同。当在t3和t4之间时,Vds=Vin(t),此外,在一个工频内,当Vin(t)<0.5Vbus,t3 电感L1必须工作在断续电流模式下,以实现自动PFC,因此,为保证在最糟糕的情况下仍可实现DCM,参数设计选取90-Vac 输入下进行。LED 驱动器的参数设计为输出功率为60 W,输出电流为2.0 A,Tline=20 ms,ω=2π×50 rad/s,vinpk=127.3 V,Ts=10 μs。前级Boost 变换器的设计分为如下四步: (1)根据MOSFET 所需的电压范围选定合适的Ntf和Ds,在本文的设计中,Ntf设为1,Ds根据DCM工作约束条件设定,为了满足Ds+D′≤1 的条件,在90 Vac额定负载下,Ds设为0.189。假设Ds和Vbus在开关频率内恒为定值,则根据公式(8)可得Vbus=159 V。 (2)确保Ds能满足DCM 工作条件,根据公式(6),在Vin(t)达到最大值时D′最大。 式中:临界导通模式(BCM)下,D′max满足D′max=1-Ds,因此,由公式(11)得Vbus的最小值是157 V,如果Vbus小于此最小值,则返回第一步,调整Ds参数。 (3)设计变压器Tf参数,铁芯采用PQ20/20,加入较小气隙以减少漏磁并避免磁通饱和,为了平衡铁芯和铜损耗,初级绕组为30 匝,电感Lm设为575 μH。 (4)由公式(10)可得L1=80 μH,以确保初级变换器工作于DCM,后级电感L2应足够大以确保后级工作于CCM 模式下,其关系如下 上述的四步设计需要在DCM 约束条件满足前反复进行,以确保Vbus不会引起过高的电压应力。 本文所提出的改进型填谷电路的设计包括开关管、二极管和电容的选型,观察图1,开关管S1开路时,会产生高的电压应力,此时S1与电容C2并联,其值为0.5Vbus,其中本文电路其电压应力为270 V,小于300 V。当工作在模态1 时,由于N1和C2的电压相等,方向相反,D6阴极电势接近于地,其阳极电压为0.5Vbus。因此,D6的应力仅为0.5Vbus。当S1闭合时,D6应力为2Vbus,约为450 V。上述分析表明,本文设计的变换器中,D6的电压应力大幅减小。 电容选型基于低频电压纹波幅值,因为储存电容的主要作用是平衡脉冲输入和稳定输出。当Po,ω和Vbus保持为恒值时,输入电容Cin和电压纹波幅值Δvbus的关系如式(13)。 在给定的电压纹波ΔVbus下,式(13)可用于估算电容值。 调光功能在照明领域是实现节能减排的必要环节,LED 的亮度近似成比例于平均电流,因此,DPWM 控制策略可用于调节平均输出电流,图5 为控制器基本框图和关键波形。图4 中,S2受控于VGS2,由低频选通信号和高频门信号运算得到。Io的幅值由Vcon调制,平均输出电流Io受Vdim调整。门信号Vcon由二极管电流iDs1和预期输出电流Ioref经比较器产生。iDs1作为Io的反馈信号,与Io具有相同的振幅,在开关频率处跳转。最后,iDs1受电流互感器检测,并发送到比较器。 图4 调光电路控制模型 Vdim和io的理论波形如图5 所示。Vdim为低电平时,开关S2关断,灯同时熄灭,在Vdim恢复高电平时重新点亮。因此,LED 的亮度调节通过改变Vdim的导通宽度实现,调光频率应超过200 Hz,以避免灯光闪烁带来的视觉疲劳[18]。 图5 变换器的主要波形 为了验证本文提出的LED 驱动器的有效性,论文在PSIM 平台上进行了仿真验证。电路仿真参数见表1。此外,图6 为所提结构的仿真拓扑。 图6 仿真拓扑图 表1 器件参数 图7 分别给出了Vs=110 V 和Vs=220 V 时的仿真波形。可以看出,输入电流和电压基本保持相同相位;此外,实测在不同输入电压下的功率因数分别为98.83%和99.17%,其值远远满足Energy-star对电器设备的要求。 图7 不同输入电压下的输入电流波形 由于LED 为电流型器件,输出电流的性能为系统的重要衡量标准。对此,图8 给出了Vs=110 V和Vs=220 V 时的输出电流波形。观察图8(a),电路3 ms 内达到稳定,验证了所提电路快速的动态响应性能。另一种情况如图8(b)所示,此时输入电压为220 V,此时输出电流稳定在1.4 A,其纹波电流约为40 mA。满足LED 对驱动器电流纹波在20%以下的要求,证明所提LED 驱动器拥有较好的输出性能。 图8 不同输入电压下的输出电流波形 为进一步验证所提电路的正确性和可行性,搭建了100 W 实验样机,且实验参数与仿真相同。 图9(a)和图9(b)为输入电压有效值为110 V 和90 V 时,测得相应的输入电流的实验波形。由图9 可知,输入电流的包络线可近似看做一条正弦波,且输出电压和电流相位几乎重叠。采用TEK 功率因数分析仪PA3000 对满载时功率因数和输入电流谐波含量进行测量,其测量结果分别为99.3%和98.7%;其谐波含量分别为3.9%和4.8%。输入电流虽略有畸变,但谐波含量均小于5%。 图9 输入电压和电流的实验波形 图10 为在开关频率下输入电流的实测波形。由图10 可知,输入电流明显工作在断续状态(DCM)。因此,后级二极管的反向恢复时间被消除,其传递效率得到进一步提升。 图10 开关频率下的输出电流的测量波形 为满足节能的要求,LED 驱动器大范围且稳定的亮度调节是其判断性能的重要指标。图11(a)和图11(b)为通过对开关管S2进行PWM 调节得到的输出电流的实验波形。由图11(a)和图11(b)可知,开关管S1占空比为0.27 和0.43 时,其输出电流的幅值分别稳定在1 A 和1.5 A。此外,输出电流的峰-谷值与平均值的比值分别为6.9%和7.2%。因此,所提驱动器将不存在频闪现象。图11(c)为亮度调节的动态过程;其快速的动态响应验证了控制单元设计的正确性。 图11 输出电流的实验波形 由于削峰填谷电路经常用于日常照明电源的AC/DC 功率变换器场合,而目前文献[15]的方案多被采用。因此,将本文与文献[15]所提电路在不同的电压等级下进行了效率测试,其结果如图12 所示。图12 中,所提电路的效率在各个测试点几乎均高于文献[15],并在输入电压的有效值为85 V 时达到其峰值效率91.3%。 图12 不同输入电压下的转换效率 本文提出了一种基于Boost 的新型单级AC-DC变换器,引入了优化的填谷电路,并加入一选择开关以获得最优性能,解决了该变换器的固有电压应力问题,可在工程实践中推广应用。其他主要优点包括高功率因数、电容和主要开关上的较低的电压应力。相比于传统变换器的设计,本文对改进的填谷电路设计过程做出详细讨论和分析。最后,仿真和实验结果表明,本文设计的变换器具有很好的实用性,并为工程实践提供了有力支持。2 参数设计和控制策略
2.1 前级Boost 变换器设计
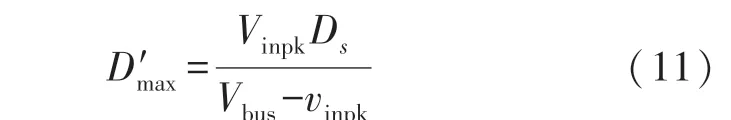
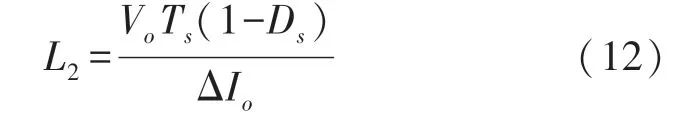
2.2 填谷电路的参数设计

2.3 DPWM 控制与实现
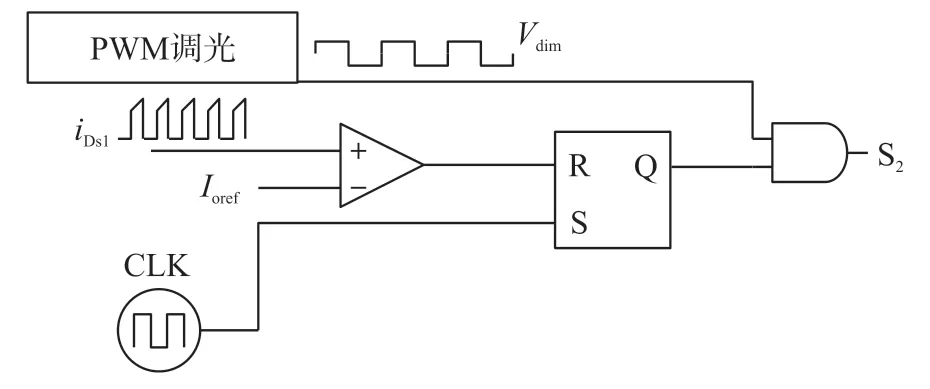

3 仿真和实验结果
3.1 仿真验证
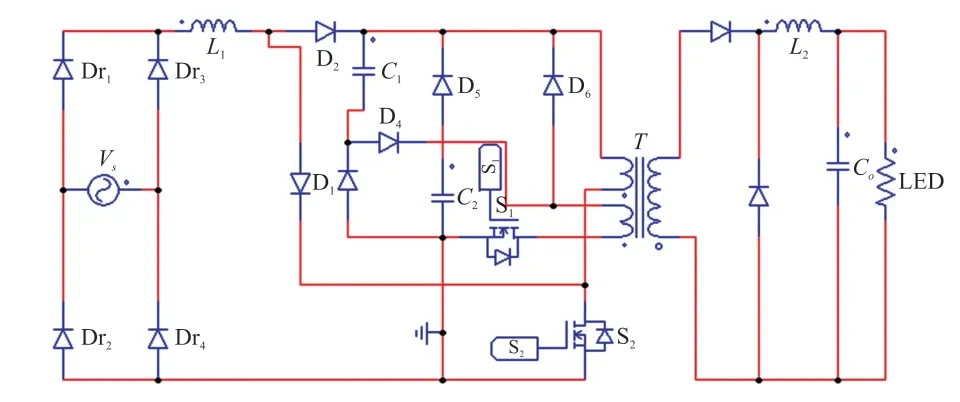


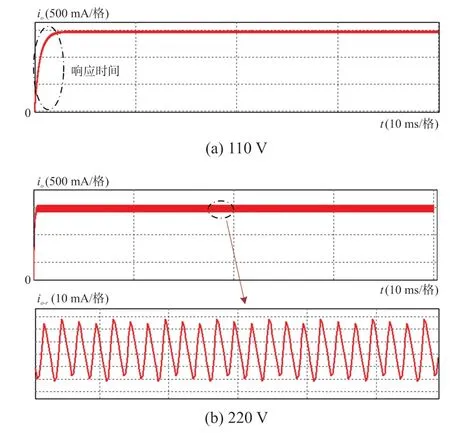
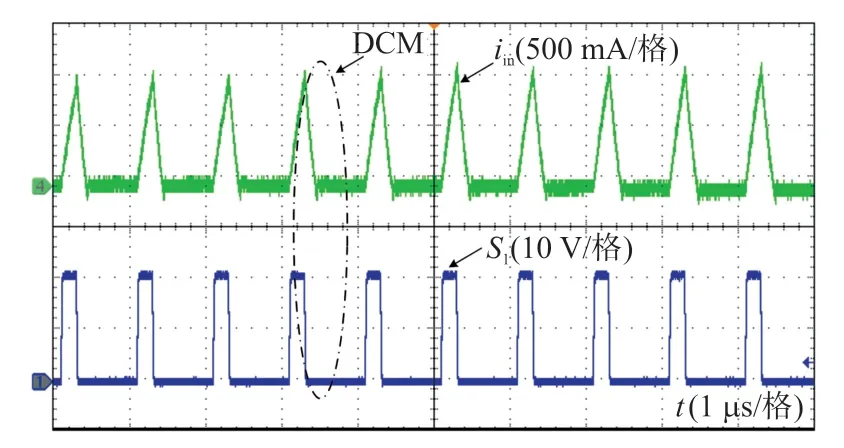
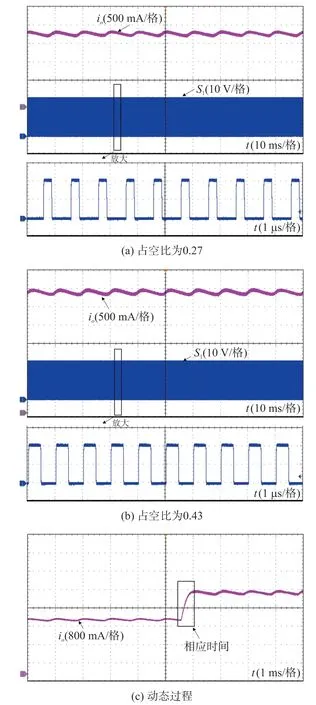
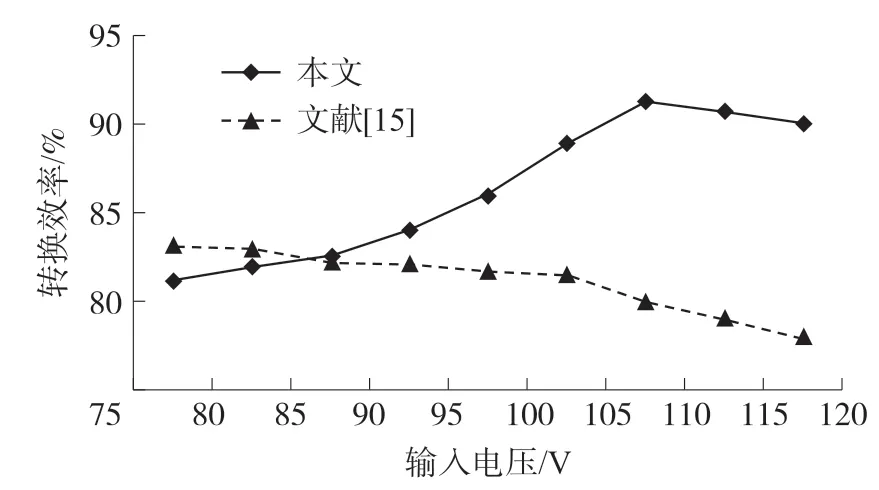
3.2 实验结果
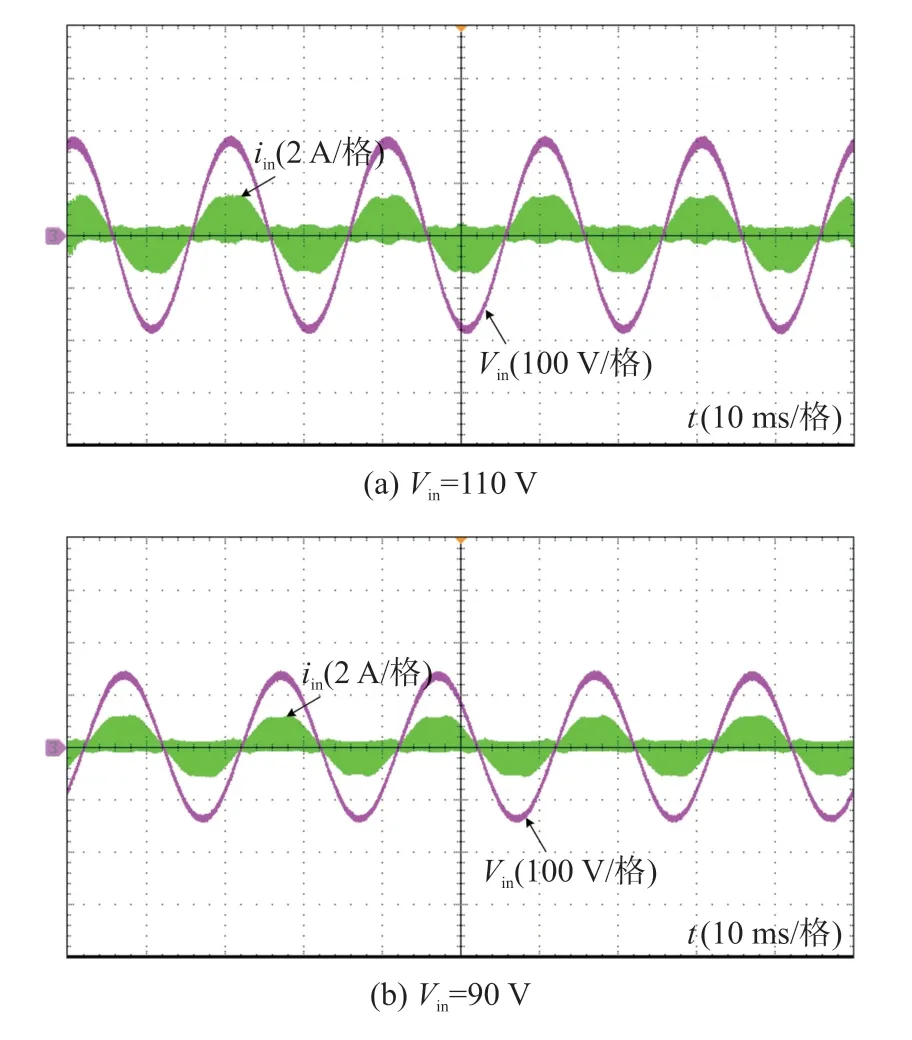
4 结论

