U形管内浆体输送特性研究

栗涛杰， 肖兰兰， 杨兆霞， 刘学文*

(1.上海工程技术大学 机械与汽车工程学院， 上海 201620； 2.中国人民解放军95958部队， 上海 200120)

因为地理环境的影响，结构简单且能改变方向的U形管广泛应用于各种管线中[1]。对于浆体来说水力运输是一种好的选择，但管道中砂粒的存在会影响浆体的运输，如砂粒在管道中的沉积会造成管道流通的有效面积减小，从而出现压力损失增加、局部高速及部分或全部堵塞等情况，造成产量下降或管道损坏，导致需要昂贵的清洗作业[2-3]。学者们研究了流体中的颗粒杂质在管道中的流动形式，Ntow O T等[4]对各种湍流模型如κ-epsilon (κ-ε)、κ-omega (κ-ω)、SSG雷诺应力、剪切应力输运和涡动黏度输运的鲁棒性进行了测试，以预测颗粒体积分数分布的实验数据对压降的影响。徐鹏飞等[5]研究得到一个合适的水流速度能有效的提高矿石的开采率，大于这个水流速度会降低效率，低于这个水流速度则导致砂粒堆积。马光飞等[6]研究得出颗粒密度影响能量损失的结论。孙贤等[7]研究得出浆体的速度与颗粒的粒径都会影响水合物的最大体积分数，当管径大于200 mm时，颗粒直径对水合物的最大体积分数影响几乎不变。曹斌等[8]研究得出颗粒的受力情况由颗粒速度与流体速度共同决定。寇子超[9]建立了浆体运输模型，研究不同的浆体浓度对压力损失的影响，得出管内浆体固体体积分数的分布对压力损失有很大的影响。吴优等[10]通过研究摩擦阻力与管径的关系，得出管道管径越小摩擦阻力越大。牛骏等[11]研究得出随流速的增加，能带出更大范围颗粒直径，提升了携出效果。张好林等[12]研究得出岩屑运动所需要的速度与冲砂洗井临界速度与岩屑的直径成正相关。

随着计算技术的发展，计算流体动力学(CFD)得到广泛应用[13-14]，与实验相比，计算不仅周期短而且成本低。CFD模拟为解决复杂的流体流动问题提供了一种经济有效的方法。李安等[15]研究了临界速度与浆体内颗粒体积分数的关系，得出临界速度随浆体内颗粒体积分数的变化基本不变。张自超等[16]研究得出固相速度、体积分数的分布受进口速度和固体体积分数变化的影响。浆体管道内的流动不同于单相管道流动，因为固相的存在会导致其流动特性发生极端变化。当浆体速度与颗粒体积分数发生改变时，将加剧对弯头的冲击磨损，同时会影响管道沿程阻力损失。课题组针对不同质量分数浆体在U形弯管内的流动情况，采用多相流混合模型对三维弯管进行数值模拟，探究浆体的流动特性以及参数改变对压降损失的影响。

1 模型的建立

1.1 物理模型

图1(a)所示为U形管物理模型，模型包括入口段、弯头段和出口段3部分。其中管道的水力直径为40 mm，弯管的曲率半径为300 mm，入口段的长度L1为1 800 mm，出口段的长度L2为1 800 mm。通过Mesh软件对模型进行网格划分，弯头的网格划分如图1(b)所示。选取密度为998.2 kg/m3的水作为液相，颗粒密度为2 218 kg/m3[17]，颗粒质量分数Cw为30%～60%；颗粒的粒径为40 μm、颗粒质量分数为30%、流速为2.5 m/s；重力加速度方向为沿z轴的负方向。

1.2 控制方程

课题组采用多相流混合模型求解，该模型的连续方程、动量守恒方程如下：

1) 连续性方程

根据质量守恒定律，可得混合模型的连续方程：

(1)

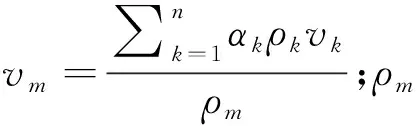
2) 动量守恒方程

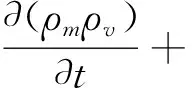
(2)

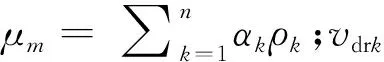
1.3 数值模拟

以速度入口定义管道入口条件，管道的出口为自由出流边界，壁面为无滑移边界条件。基于压力基求解，湍流模型选取了计算速度快、易于收敛的标准κ-ε[18]模型，近壁面区域的流动采用标准壁面函数进行求解，压力速度耦合采用SIMPLE算法，在整个区域内实现了较高的数值解精度。

1.4 网格的无关性验证

图2所示为网格无关性验证。图2中对6种不同数量的网格进行计算，结果发现当网格数达到17万时，继续增加网格的数量，c截面处水平直径方向上的静压几乎没有变化，而且网格继续增加对结果影响不明显。为了保证计算结果的准确性，同时又能节约计算资源，选择居于中间的25万的网格进行计算。

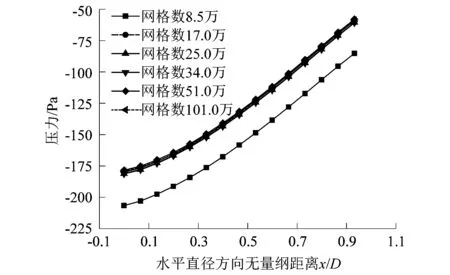
图2 网格无关性验证Figure 2 Independence validation of grid

2 结果与分析

2.1 弯头处二次流现象分析

图3所示为弯管不同截面压强分布(右侧为弯管的外侧)，由图3(a)可得入口段管内总压分布为中间大外侧小，由3(b)和(c)可以得到流经弯头时，由于浆体受到离心力的作用，弯头中心的浆体不断向外侧运动，弯管总压高的外侧流体同时向弯头的内侧行补充从而形成图3(d)的二次流。

图3 弯管不同位置处横截面总压分布Figure 3 Total pressure distribution of cross section at different positions of elbow

2.2 颗粒速度和体积分数分布

2.2.1 颗粒体积分数分布

图4所示为弯管不同截面处颗粒体积分数分布，在入口段管内颗粒体积分数在水平方向上几乎呈对称分布，由于重力的作用在管内呈现上侧颗粒的体积分数小于下侧的体积分数，随着流体的运动，b截面处底部颗粒的体积分数明显大于a截面处颗粒的体积分数。当流体进入弯头，受离心力的作用颗粒向外侧运动，在c和d截面处二次流形成漩涡，进而带动固体颗粒向弯头的内侧运动，使得底部内侧的颗粒体积分数高于外侧的颗粒体积分数。当流体进入出口段时，由于受二次流作用而逐渐减弱，但颗粒体积分数分布与直管中相比仍表现出一定程度的倾斜。

图4 弯管不同位置处横截面颗粒体积分数分布Figure 4 Cross-sectional particle volume fraction distribution at different positions of elbow

2.2.2 颗粒速度分布

图5所示为弯管不同截面颗粒速度分布，在直管入口段处，颗粒速度沿管道中心线近似对称，表现为中间大于壁面速度。受二次流的影响，由原来的中心对称变为一定程度偏离中心截面，截面内侧颗体积分数高于外侧的体积分数，颗粒的质量分数大导致颗粒速度减小。当流体进入弯管的出口段，由于没有离心力的作用，因而颗粒的速度慢慢恢复到对称分布。

图5 弯管不同位置处横截面颗粒速度分布Figure 5 Cross-sectional velocity distribution of particles at different positions of elbow

2.2.3 不同速度下c截面颗粒体积分数分布

图6所示为不同速度下c截面颗粒体积分数分布，图中不同流速下管道内颗粒体积分数的分布。浆体中颗粒受离心力作用向外侧运动，同时由于二次流的作用使得底部内侧的颗粒体积分数高于外侧的颗粒体积分数。随着水流速度逐渐增大，且浆体中颗粒受到自身重量影响，水流速度越小，外侧颗粒越少，随着速度增大，受二次流影响，管外侧颗粒的体积分数高于管内侧颗粒的体积分数。

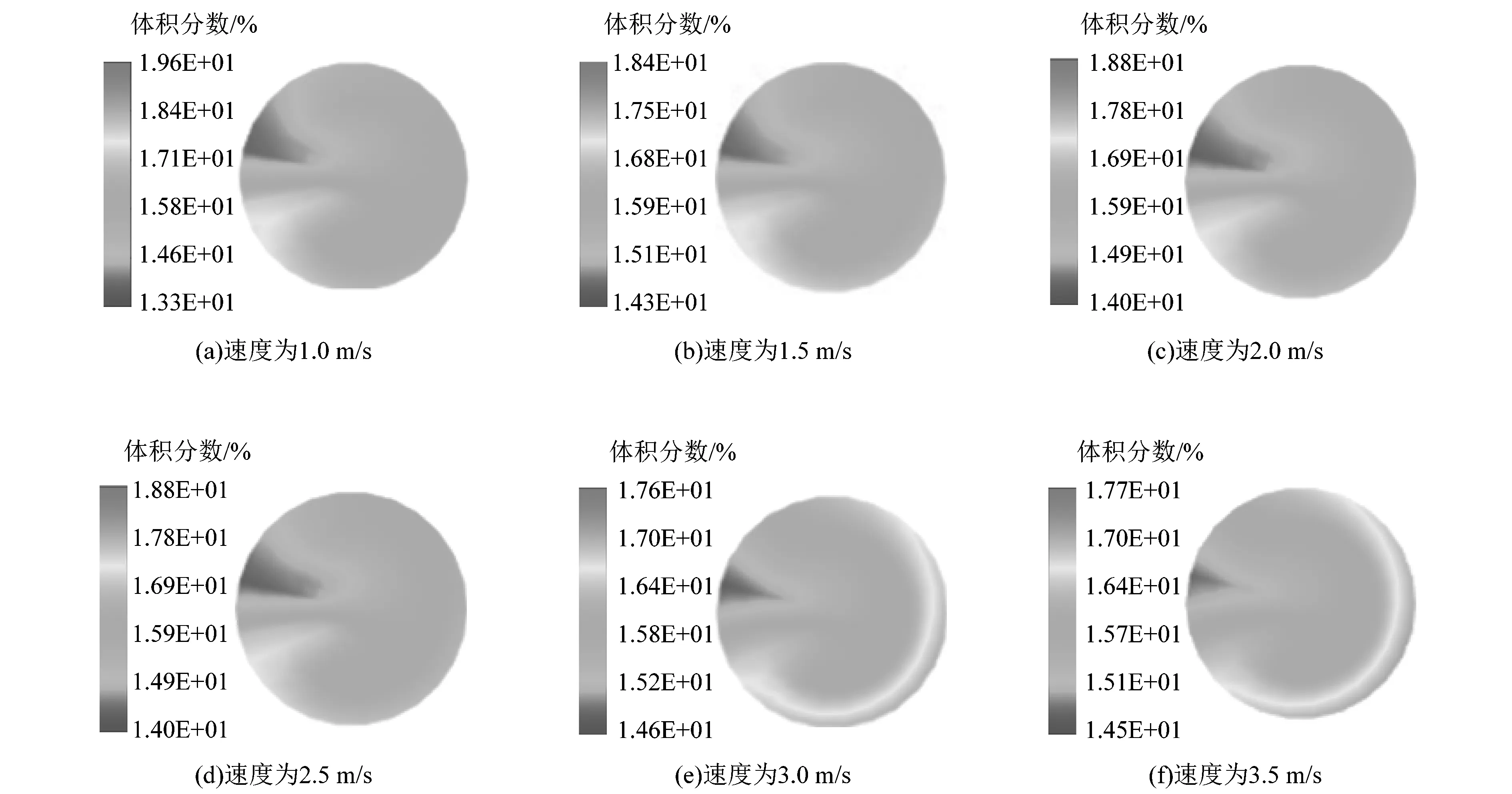
图6 不同速度下颗粒体积分数分布Figure 6 Particle volume fraction distribution at different velocities

2.3 压降特性

2.3.1 进出口压降与颗粒质量分数和速度的关系

图7所示为进出口压降与速度和质量分数关系分布情况，当颗粒质量分数为30%，40%，50%和60%时，浆体流速为1.0～3.5 m/s，可以观察到在任何给定的颗粒质量分数，压降随速度的增加而增加，在速度较高时，压降的增加速度更明显。研究还发现，颗粒质量分数较大时压降的增加速度比颗粒质量分数增加要快，而且直接取决于浆体悬浮液的流动性质。

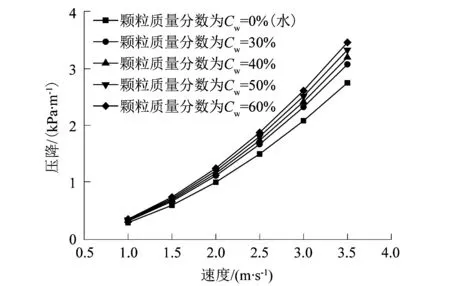
图7 不同质量分数下压降和速度的关系Figure 7 Relactionship between pressure drop and velocity under different mass fractions

2.3.2 进出口压降与管径关系

压降损失为：

ΔP=ρλ(L/d)u2/2。

(3)

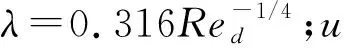
图8所示为进出口压降与管径关系分布。为了进一步了解管道进出口压降与管道直径的关系，选取颗粒质量分数为60%和直径分别为30，40，50和60 mm 4种工况进行计算。由流体力学知识可得管道沿程阻力损失随管径的增加而减小。图8中压降随管径的增加呈减小的趋势符合沿程阻力损失规律。

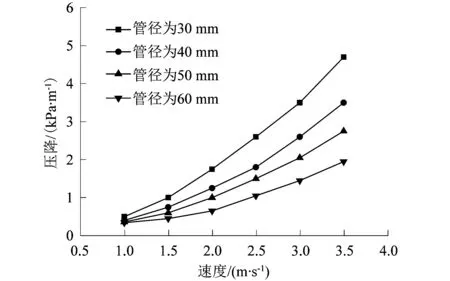
图8 不同管径下压降和速度的关系Figure 8 Relactionship between pressure drop and velocity under different pipe diameters

3 结论

课题组采用FLUENT软件对U形管内部流场进行模拟，研究了管内颗粒体积分数和速度的分布，以及颗粒体积分数、速度和管径对管内压降的影响，得出了以下结论：

1) 对于U形管流型而言，在入口段颗粒体积分数分布均匀，进入弯管段颗粒体积分数表现出一定的梯度；同时进入弯头靠近管道内侧的高速流区域，沿着流动方向逐渐向管道外侧移动。浆体流过弯头后，管内颗粒速度与体积分数分布状态很快恢复原来状态。

2) 在一定工况下，管内浆体在运送过程中的压降受管径、颗粒的质量分数和速度共同作用。管内压降随管径增大而变小；相同颗粒速度条件下，管内压降随颗粒质量分数变化波动小；相同颗粒质量分数条件下，管内压降随颗粒速度增大呈线性分布；颗粒的质量分数和速度同时增大，会引起管内压降明显变化。

课题组通过动力学仿真及分析，为管内流型变化提供了参考，其他条件对浆体运输压降的影响仍需进一步开展。