多自由度弧面分度凸轮机构动力学研究

贲晨阳， 何雪明，2， 刘 超

(1.江南大学 机械工程学院， 江苏 无锡 214122；2.江南大学 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122)

为了能够让弧面分度凸轮机构以更加平稳、高效和精度更高的方式运行，缩小国内与国外产品间的差距，弧面分度凸轮机构的动力学性能越来越受研究人员的关注。国内外专家学者对弧面分度凸轮机构的动力学方面进行了研究：张三等[1]对弧面分度凸轮进行瞬态动力学分析，得到分度期内工作轮廓曲面和转盘滚子曲面的动态接触应力分布及其变化规律；刘言松等[2]结合多体动力学并运用虚拟样机对弧面分度凸轮机构进行了动力学方面的研究；冯立艳等[3]通过模态分析得到转盘轴的固有频率和振型图，为弧面分度凸轮机构后续动力学研究提供重要参考；赵世田等[4]提出基于齐次坐标变换的通用圆锥滚子弧面分度凸轮轮廓曲面方程建立方法；M. Chew等[5]和Y.S.Unlusoy等[6]提出了凸轮机构的单自由度和双自由度模型的综合理论；Ching-Haun Tseng等[7]建立数学模型验证了凸轮与滚子间的间隙对角加速度的影响；王其超等[8]建立凸轮机构的单、双自由度振动模型，从而建立动态响应方程。

由于机构运转时具有较高的转速，各构件的惯性力不断增加，导致动力学响应变大。因此，机构中从动件的动力学响应与理论有很大的偏差。所以，对分度凸轮机构，仅从运动学方面考虑已经不能解决工程的实际问题，因此需要对其在动力学方面进行深入的研究。

1 设计模型

弧面分度凸轮机构三维模型如图1所示，通过弧面分度凸轮轮廓面与滚子间的啮合作用，实现分度盘的转动。

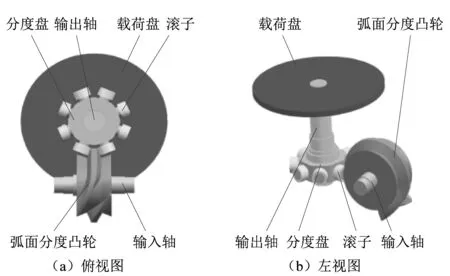
图1 弧面分度凸轮机构的三维模型Figure 1 Three-dimensional model of arcuate indexing cam mechanism

1.1 弧面分度凸轮机构动力学模型假定

由于弧面分度凸轮机构的动力学性能受诸多因素的影响，为了深入研究凸轮机构的动力学性能的影响因素，以弧面分度凸轮机构的主要特征为基础，对弧面分度凸轮机构的动力学模型进行简化，对模型做以下假定:

1) 忽略前置装置对弧面分度凸轮机构的影响，假定弧面分度凸轮等速回转[9]；

2) 假定弧面分度凸轮与均匀安装在分度盘上的滚子可实现理想的无间隙啮合；

3) 将分度盘、弧面分度凸轮、载荷盘和滚子视作刚性体，本身的弹性变形忽略不计，将输入轴和输出轴视为弹性体；

4) 将弧面分度凸轮、载荷盘和分度盘视为等效集中质量体；

5) 弧面分度凸轮廓面加工精确，无制造和安装误差。

1.2 动力学模型

根据集中质量法，课题组建立多自由度的弧面分度凸轮机构的动力学模型，以解决符合实际情况的动力学模型建立和求解复杂的问题。

如图2所示，对输入轴系统(包括输入轴和凸面分度凸轮)进行扭转振动分析时，把输入轴系统看作是以弧面分度凸轮的质量为质量块的扭转系统，等效转动惯量为J1。在分析输入轴系统的横向振动时，将输入轴系统看作以凸轮的等效质量为m1的质量块，研究其中x,z轴方向上的横向振动。

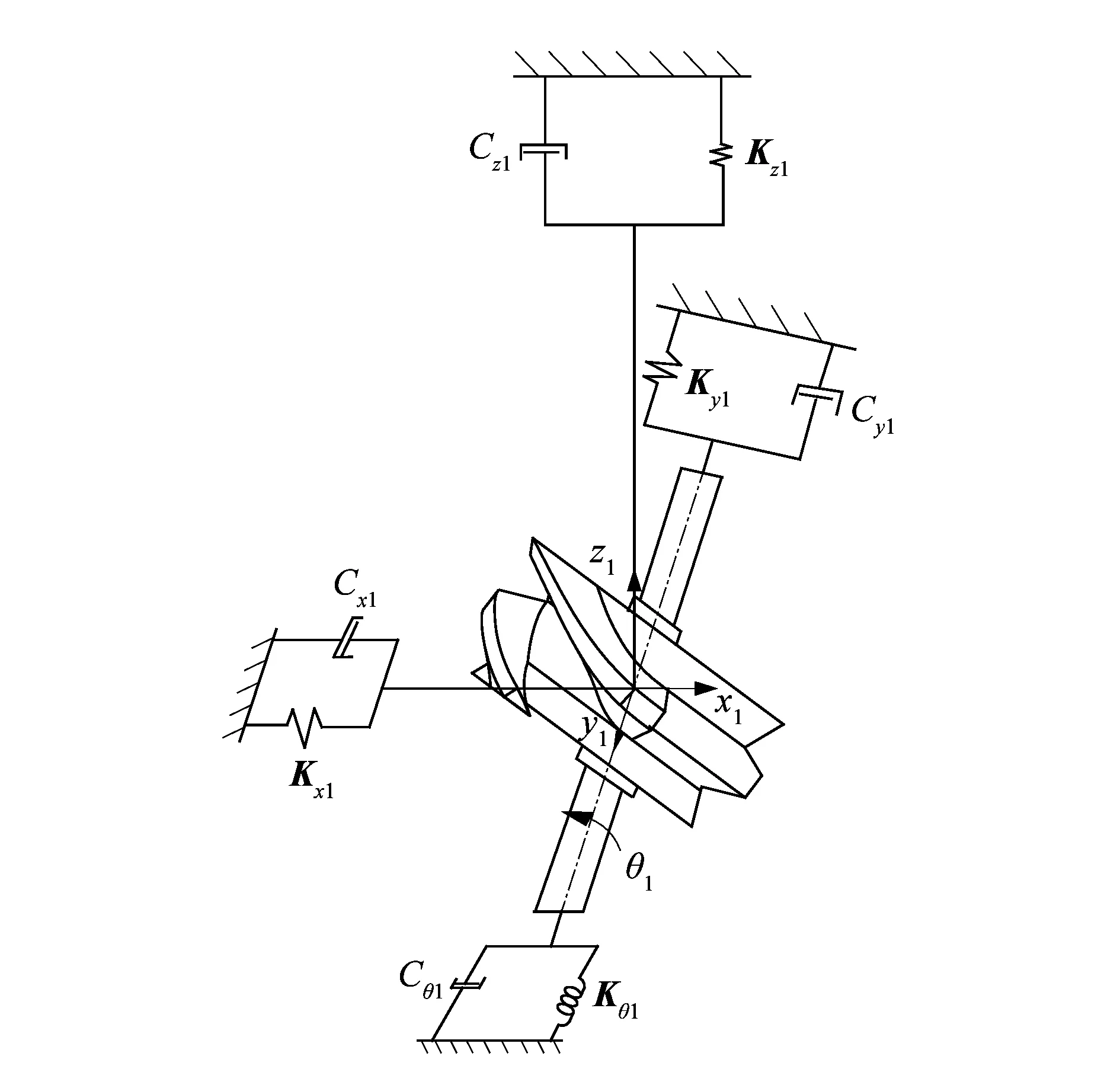
图2 4自由度的输入轴系统动力学模型Figure 2 Dynamic model of input shaft system with 4 degrees of freedom

图2中：Cz1为输入轴沿z轴方向上的阻尼系数；Kx1,Ky1，Kz1分别为输入轴沿x轴，y轴，z轴方向上的弯曲刚度；Cx1，Cy1，Cz1分别为输入轴沿x轴，y轴，z轴方向上的振动阻尼系数；Kx1为输入轴沿x轴方向上的振动刚度；Cθ1为输入轴扭转阻尼系数；Kθ1为输入轴扭转刚度；θ1为凸轮转角。

在分析输入轴系统的轴向振动时，将输入轴系统看做以凸轮的等效质量为质量块，研究其在y轴方向上的轴向振动。

如图3所示，对于输出轴系统(包括输出轴、载荷盘、滚子和分度盘)进行分析时，在分析扭转振动时，将其看作以分度盘等效转动惯量J2和载荷盘的等效转动惯量J1为质量块的双质量扭转系统。在分析其横向振动时，将其看作为各分度盘的等效质量m2与载荷盘的等效质量m3为质量块的简支梁，研究其在x，y轴方向上的横向振动。在分析输出轴系统的轴向振动时，将输出轴系统看作以me(me=m2+m3)为质量块的轴向振动，研究其在输出轴z方向上的轴向振动。

图3 7自由度的输出轴系统动力学模型Figure 3 Dynamic model of output shaft system with 7 degrees of freedom

其中：m3和J3分别为载荷盘等效质量和等效转动惯量；θ3为载荷盘转角；K22，K33分别为分度盘和载荷盘在x轴和y轴上的弯曲刚度；K23为分度盘振动对载荷盘在x和y轴上弯曲刚度；K32为载荷盘振动对分度盘在x和y轴上弯曲刚度；Cθ2为输出轴扭转阻尼系数；Kθ2输出轴扭转刚度；m2和J2分别为分度盘等效质量和等效转动惯量；θ2为分度盘实际转角；Cz23为输出轴在z轴上的振动阻尼系数；Kz23为输出轴系统在z轴方向上的等效刚度；Cf2为分度盘的扭转阻尼系数。

将输入轴系统模型与输出轴系统间耦合，建立11个自由度的弧面分度凸轮机构动力学模型如图4所示。

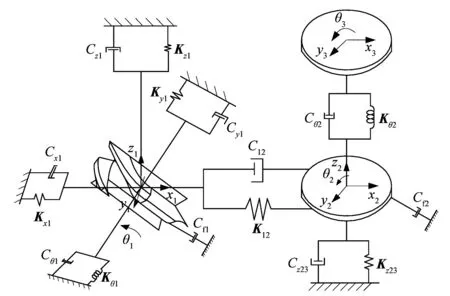
图4 11自由度的弧面分度凸轮机构动力学模型Figure 4 Dynamic model of globular indexing cam mechanism with 11 degrees of freedom

图4中：K12和C12分别为凸轮与滚子间的等效接触刚度与等效接触阻尼系数；Cf1为凸轮的扭转阻尼系数；Cz23为输出轴系统在z轴方向上的振动阻尼系数。

凸轮与滚子的接触刚度，主要与凸轮自身的刚度、滚子轴的刚度以及滚子的弯曲刚度等因素有关。凸轮与滚子间的接触刚度随着位置的变化而变化。凸轮与滚子接触时可以看作2个柱体的相互接触。基于赫兹理论进行刚度计算有：

(1)

式中：P为接触区长度方向上的单位力；H为接触变形量总和；h1和h2分别为凸轮与滚子的接触变形量，且有

(2)

(3)

式中：ρ1，ρ2分别为凸轮与滚子在接触点处的曲率半径；b为凸轮与滚子的接触宽度，且

(4)

式中：μ1，μ2分别为凸轮与滚子的泊松比；E1,E2分别为凸轮与滚子的弹性模量；L为接触区长度。

2 动力学方程

2.1 弧面分度凸轮机构系统能量的计算

考虑弧面分度凸轮机构的横向、扭转和轴向变形，系统的位移列阵X为：

X=[θ1θ2θ3x1y1z1x2y2x3y3z23]T。

(5)

式中：θ1，θ2，θ3分别为凸轮、分度盘和载荷盘的实际转角；x1，y1，z1为凸轮沿x，y，z轴方向上的线位移；x2，y2为分度盘沿x，y轴方向上的线位移；x3，y3为载荷盘沿x，y轴方向上的线位移；z23为输出轴系统(载荷盘和分度盘)沿z轴方向上的线位移。

应用拉格朗日方程法来建立弧面分度凸轮机构动力学方程，该方法以机构的系统能量守恒为基础，将机构的动能、势能和耗散能联系起来[10]。所以，需要对机构中各个能量进行求解。

1) 机构的动能求解

①凸轮的动能

(6)

②分度盘的动能

(7)

③载荷盘的动能

(8)

2) 机构的势能求解

①凸轮的势能

(9)

②分度盘的势能

(10)

③载荷盘的势能

(11)

④载荷盘与分度盘弯振耦合势能

(12)

(13)

⑤输出轴与输入轴系统的耦合势能

(14)

3) 机构的耗散能求解

①输入轴系统的耗散能

(15)

②输出轴系统的势能耗散

(16)

③输入轴与输出轴耦合的耗散能

(17)

2.2 弧面分度凸轮机构动力学方程的推导及线性化

拉格朗日方程式通过简单的形式推导出复杂的系统动力学方程，方程组数与系统自由度数相同。第二类拉格朗日通用方程式为:

(18)

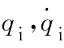
对于分度盘理论转角τ，弧面分度凸轮机构的运动规律为τ(θ1)，则有:

(19)

(20)

根据拉格朗日方程推导出的系统动力学微分方程，由于模型中考虑轴的扭转弹性变形而出现非线性项。为了便于求解计算，可将其做线性化处理[11]。

(21)

并将广义坐标θ1,θ2,θ3作变量代换：

q1=θ1-θ;

(22)

q2=θ2-τ(θ);

(23)

q3=θ3-τ(θ)。

(24)

式中：q1为输入轴在凸轮处的弹性扭转角；q2,q3为输出轴在分度盘、载荷盘处的弹性扭转角；将变量q1,q2,q3分别代入可以得到弧面分度凸轮机构动力学线性微分方程组。

(25)

3 转速划分及动力学响应

弧面分度凸轮机构动力学响应在计算过程中需要的参数如下：

1) 转动惯量

J1=6.999 600 0×10-2kg·m2；

J2=3.471 193 0×10-3kg·m2；

J3=5.985 588 1×10-2kg·m2。

2) 等效质量

m1=18.933 488 48 kg；

m2=6.126 708 82 kg；

m3=6.569 037 00 kg。

3) 等效扭转刚度

Kθ1=1.948 7×105N·m·rad-1；

Kθ2=3.502 1×105N·m·rad-1。

4) 轴向弯曲刚度

Ky1=3.882 1×108N·m；

Kz23=3.975 2×109N·m。

5) 横向弯曲刚度

Kx1=Kz1=3.185 3×108N·m；

K22=2.931 2×109N·m；

K33=6.388 8×107N·m；

K23=K32=8.467 9×108N·m。

6) 凸轮与滚子等效刚度

K12=1.232 9×106N·m。

威尔逊-θ法是求解动力学问题的一种常用方法。当θ≥1.37时，威尔逊-θ法是无条件稳定的，课题组将θ设定为1.40，应用MATLAB语言编程，对式(25)所建立的弧面分度凸轮11自由度动力学微分方程进行数值求解。

3.1 固有频率及转速划分

弧面分度凸轮机构的固有频率直接关系到机构振动的特征。在不考虑阻尼的情况下，设各阶固有频率为ωi,则机构的频率方程为：

(26)

式中：K为机构的刚度矩阵；ωi为机构的固有频率；M为机构的质量矩阵。

在弧面分度凸轮机构的运行过程中，机构的刚度矩阵随着弧面凸轮转角位置变化而不断变化。根据已得到的质量矩阵和刚度矩阵，利用MATLAB软件计算得到弧面分度凸轮机构的各阶固有频率。弧面分度凸轮机构前3阶固有频率变化曲线如图5所示。

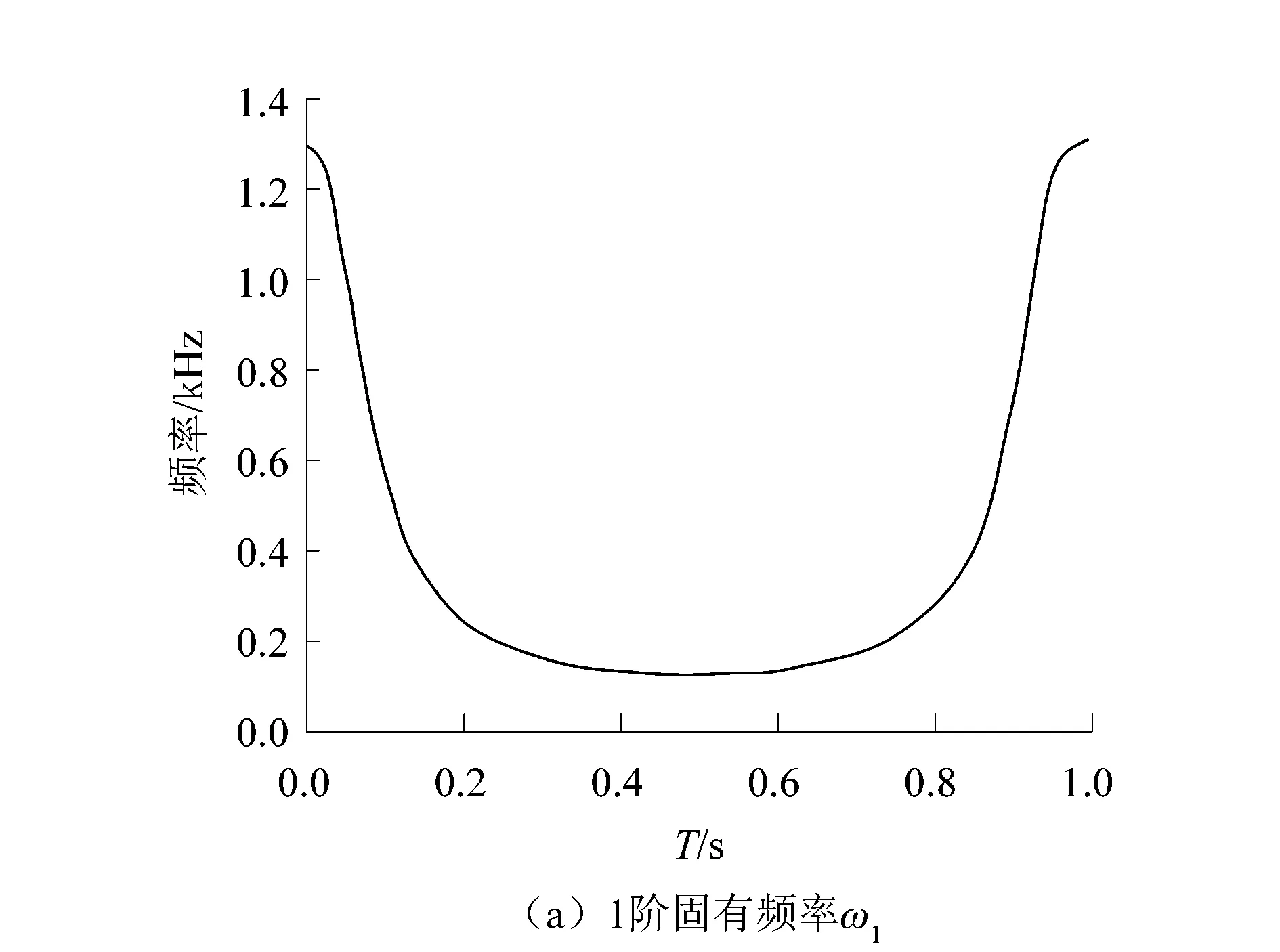
从图5可以看出，弧面分度凸轮前3阶扭转振型的固有频率与机构处在不同的工作位置有关。而后8阶为横向振动和轴向振动对应的振型。一般来说，高阶频率对系统动力学响应的影响很小，故在求解系统的振动响应时，高阶频率对振动响应的影响可以忽略不计。

从图5可以看出，弧面分度凸轮机构前3阶扭转振型的频率受凸轮转角变化的影响比较大。图5(a)所示为系统的1阶固有频率，其随着随凸轮转角的变化而变化，其频率最低为163.91 Hz。

由机械动力学理论知识可知，弧面分度凸轮机构的最小频率(一阶固有频率)对应的转速，为弧面分度凸轮机构的1阶临界转速n1。

n1=60×163.91=9 834.60 r/min。

当弧面分度凸轮机构转速与此转速相等或者接近时，便会产生剧烈的振动。所以，在运行时要避开这一转速。同时，可以计算出弧面分度凸轮机构低速和中速的临界值n2、中速和高速的临界值n3以及低速、中速和高速分别对应的范围[12]：

当λ=15时，

n2=n1/λ=9 834.60/15=655.64 r/min；

当λ=6时，

n3=n1/λ=9 834.60/6=1 639.10 r/min。

λ为划分转速区间的系数。根据计算得出，当弧面分度凸轮机构转速在0～655.64 r/min范围内，为低速状态；当机构弧面分度凸轮机构转速在655.64～1 639.10 r/min范围内，为中速状态；当弧面分度凸轮机构转速大于1 639.10 r/min，为高速状态。

3.2 动力学响应

弧面分度凸轮机构载荷盘角加速度是反映机构动力学性能的一个重要指标。因此，在分析参数变化对机构动力学响应的影响时，采用载荷盘角加速度随机构参数的变化响应情况来描述机构动力学性能的变化情况。

由上文对转速的划分，分别对低、中、高速状态下载荷盘角加速度的响应进行分析。设定分度角为45°，动程角为300°，输出轴直径为60 mm，研究输入轴转速分别为低速、中速和高速状态下载荷盘角加速度的响应。

从图6和图7中可以看出，载荷盘的角加速度响应随着输入轴转速的增加呈逐渐上升的趋势。而且，在不同的速度阶段，其增长的速度也有所不同。

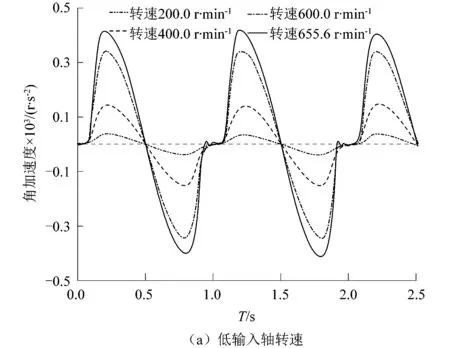
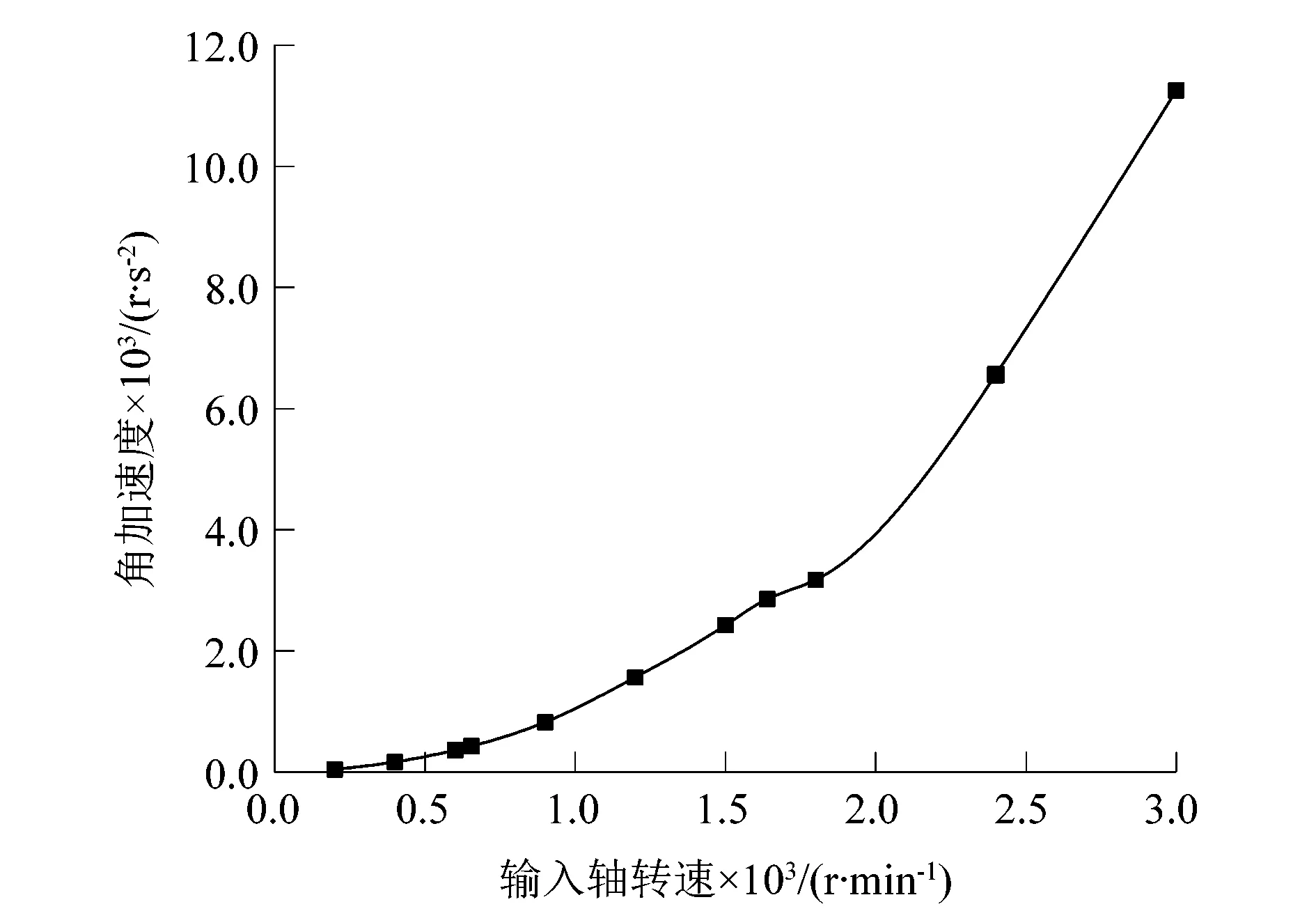
图7 输入轴转速与载荷盘角加速度最大值间的变化趋势Figure 7 Change trend between input shaft speed and maximum angular acceleration of load plate

在低速阶段，载荷盘角加速度的增加趋势比较平缓，从38.9 r/s2到427.5 r/s2；在中速阶段，角加速度从427.5 r/s2增加到2 852.4 r/s2，其趋势有明显的增加；而在高速工况下，从2 852.4 r/s2增加到11 255.4 r/s2，其增加的趋势已经非常显著了。

4 结语

为对弧面分度凸轮机构进行动力学响应分析，课题组采用集中质量法，建立了11自由度的弧面分度凸轮机构的动力学模型，推导机构的动力学微分方程组，并以此求解机构的固有频率，根据固有频率划分转速区间。课题组研究了输入轴转速分别为低速、中速和高速状态下载荷盘角加速度的动力学响应，结果显示：随着输入轴转速的不断提高，载荷盘的角加速度响应的增长趋势趋于显著。本研究为弧面分度凸轮机构后续动力学研究提供了参考。后续深入研究应考虑凸轮本身的弹性变形、分度盘和载荷盘在惯性载荷下的弹性变形对输出端动力学性能的影响。