基于FCE-AHP的双螺杆压缩机综合性能研究

宋健忠， 何雪明*， 范海港， 卢立新， 林自东

(1．江南大学 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122；2.山东碧海包装材料有限公司， 山东 临沂 276600)

双螺杆压缩机因其突出的性能优势得以在各大工业部门中广泛使用。而对压缩机的性能影响最直接的便是双螺杆压缩机转子型线的设计。但针对双螺杆压缩机对设计出的转子型线性能指标仍然未实现统一的计算标准，这将会导致国内外技术交流上产生矛盾和分歧，严重阻碍了压缩机行业技术水平前进的步伐[1-2]。目前，国内外的研究学者一直以单一的转子型线性能参数：几何特性参数、热力学性能以及能效功率等参数作为对压缩机的整体性能的评判指标，这样的定性评价往往伴随着不全面性[3]。为了避免单一的转子型线性能指标评估引起的片面性和不完全性，双螺杆压缩机综合性能的研究必须要建立一套专门用于其综合性能的多因素评判体系，以突破当下的困境[4-5]，为中国工业4.0做出一点贡献。

针对双螺杆压缩机的性能评估中难以定量分析的问题，课题组提出了一种基于模糊综合评判法[6-7]和层次分析法[8]的综合性能计算方法。

1 模糊综合评判理论

1.1 模糊综合评判法的定义

模糊综合评判法(FCE)一般是指通过模糊变换原理和最大隶属度原则，就受到多种因素影响的目标作系统全面的考虑，同时对其给予评估分析[9-11]。其基本原理是通过已被确定的被评判对象的评判集和因素集，将模糊评判矩阵和权重矢量[12]加以确定后结合2因素作归一化处理[13]，借此得到模糊综合评判的结果。

而对于综合评判而言，则必须将诸多因素囊括其中，假设选取了n个和被评判对象相关联的因素，此时记因素集为U,则有：

U={u1,u2,…,un}。

(1)

式中n表示指标因素的数目。

如果对其中任何一个因素的评判根据等级情况进行表征，此时可假设系统对指标因素做了m种不同级别的评判结果，此时其评判集

V={v1,v2,…vm}。

(2)

所以，选择模糊综合评判法解决问题时最为关键的还是如何建立一个从因素集到评判集的模糊变换法则，建立

R=U×V。

(3)

对U里面的任意因素都做一个重要性判断，变换详细过程如图1所示，得到模糊判断矩阵

(4)

式中:rij为隶属度；i=1,2,…，n,表示第i个因素；j=1,2,…,m,表示第j级别评判结果。

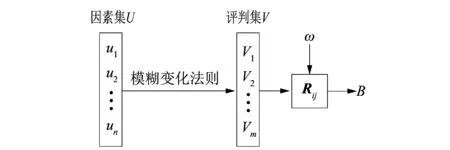
图1 模糊综合评判法Figure 1 Fuzzy comprehensive evaluation method

1.2 多级模糊综合评判法

多级模糊综合评判较为特殊，是一种基于层次评判的方式，可以较为全面的将被评估的综合指标加以反映出来，进而从整体来看有效提升了评估的效果。这可以将其应用在双螺杆压缩机性能评估中，具体如图2所示。图2中列出了双螺杆综合性能指标和相关因素的关系情况。

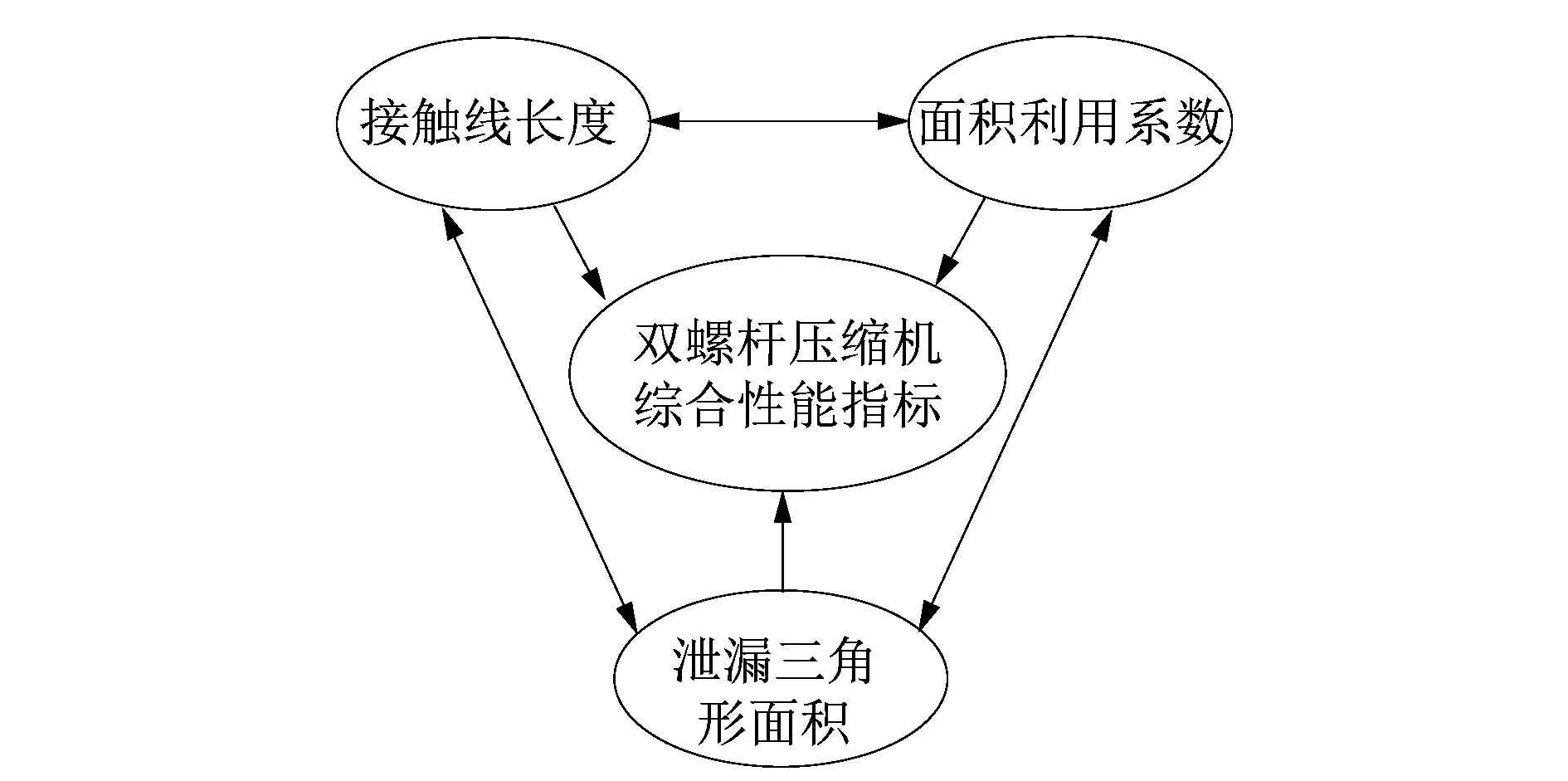
图2 双螺杆综合性能指标多级因素关系示意图Figure 2 Multi-level factor relationship diagram of comprehensive performance index of twin screw

已知评判集V和因素集U的情况下，根据模糊变换法则计算得到一个相对应的模糊评判矩阵Rij，如果需要将全部因素的综合影响考虑其中，需要对Rij里面的元素进行求和：

(5)

在所求解的Rij里面一般都选择通过对每一项Rj进行权重系数的分配，来表征因素集U里面每一个因素对综合性能指标重要程度的影响。

为体现每个元素重要程度大小，每个因素需要赋予合适的权重系数，得到集合ωi被称之为权重集。

ωi={ω1,ω2,…,ωn}。

(6)

故模糊综合评判集可由下式得到：

B=ωi·Rij=[ω1,ω2,…,ωn]·

(7)

式中：B为模糊综合评判集合，bm为双螺杆压缩机转子综合性能指标的评判结果。

2 双螺杆压缩机综合性能评估指标体系及权重的拟定

2.1 螺杆压缩机综合性能评估指标体系

课题组基于各项参数的研究构建了双螺杆压缩机综合性能评估指标体系如图3所示，将综合性能指标和影响因素，以及因素与因素之间的内在联系直观的呈现出来。

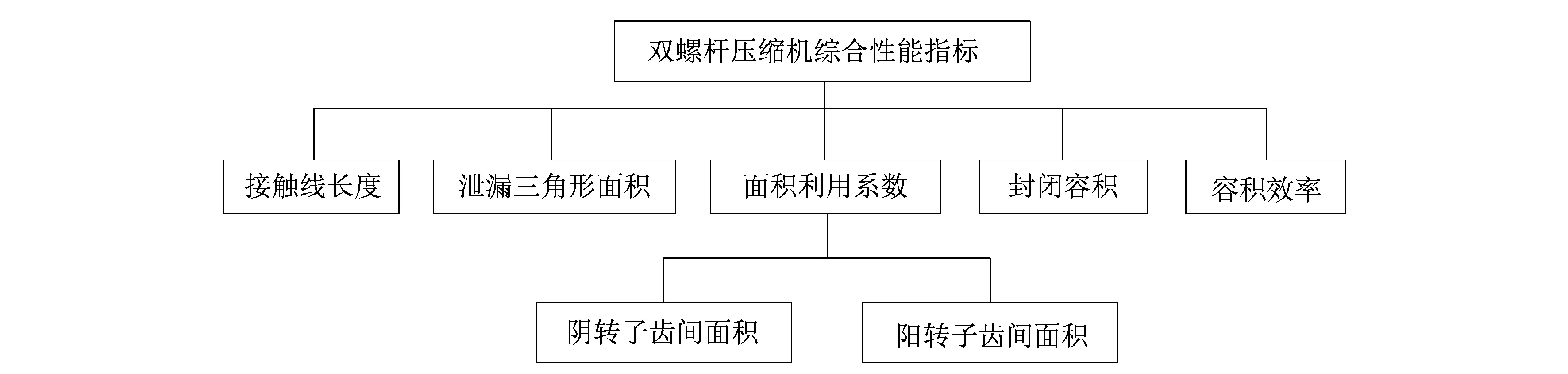
图3 双螺杆压缩机综合性能评估体系Figure 3 Comprehensive performance evaluation system of twin screw compressor

2.2 评估指标体系的权重

为确保整个评估体系的结果更有说服力，需要对每个因素的权重分配进行充分的考量并赋予合适的权重系数。表1中对常见权重确定方法的优缺点进行了分析。由表1可知层次分析法具有系统性，能够定性定量分析，计算较为简单，下面将以层次分析法进行计算。

表1 常见权重确定方法比较

2.2.1 层次分析法的基本原理

层次分析法AHP最早可追溯到美国Saaty教授。为了对各因素占比进行定量分析，尽可能减少主观意识不确定性的影响，一般可将被测对象划分为不同的因素，然后以AHP对同一层级因素做两两对比，构建判断矩阵。接下来，通过对应特征向量的归一化处理和最大特征值的计算可求解得出理想的权重矢量。最后，通过对结果进行一致性检验，分析权重分配的合理性[14]。

2.2.2 层次分析法的操作步骤：

1) 评判因素集的确定

评判因素集U={u1,u2,…un}。

2) 判断矩阵的构造

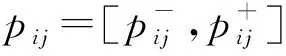
(8)

3) 权重向量的拟定和计算

为了便于计算且文中对精度要求较为宽松，故采用N次方根法求解其特征向量。

①判断矩阵各行元素之积。

(9)

式中，Mi表示判断矩阵各行元素之积。

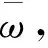
(10)

③为了下一步的一致性检验，还需要计算判断矩阵的最大特征根

(11)

式中向量Pω的第i个元素用Pω,i来表示。

4) 一致性检验

由式(10)得到权重系数，但权重的分配是否合理需要进行判断。所以必须对判断矩阵进行一致性检验，根据已有的检验公式(11)可得：

CR=CI/RI。

(12)

式中：CR为矩阵的随机一致性比率；CI为矩阵的一般一致性指标，其数值可通过公式(11)求得；RI为矩阵的平均随机一致性指标，具体取值可见表3。

(13)

式中:λmax表示矩阵的最大特征根；n表示因素集中元素的总数。

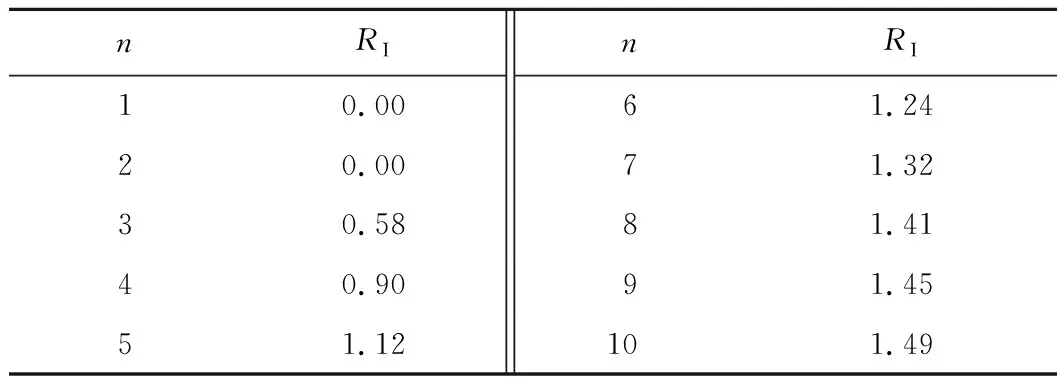
表3 随机一致性指标RI

若最终求解的判断矩阵的随机一致性比率的数值CR<0.1时，那么便认定此矩阵满足一致性，同时也表明了权重系数的分配是合理的。

3 基于双螺杆压缩机综合性能指标的啮合线研究

3.1 双螺杆压缩机综合性能评估指标求解

课题组以双螺杆压缩机作为研究对象，以模糊综合层次法进行螺杆压缩机权重系数与综合性能指标的求解。而密封性能作为压缩机最为关键的一种指标，其中面积利用系数M、泄露三角形面积S以及接触线长度L对其影响最为显著，所以选择这3种因素用作双螺杆压缩机综合性能的评估。

为便于表达，课题组用K代表综合性能指标，用L表示接触线长度，S表示泄露三角形的面积，M表示面积利用系数，建立压缩机综合性能评估体系的因素集U={L,S,M}。

1) 构造模糊判断矩阵

由于判断矩阵基于互反性1～9标度规则建立而成的。因此根据表2，以各因素的隶属度为行，可以构成模糊判断矩阵P=(pij)n×m。双螺杆压缩机综合性能指标隶属度如表4所示。

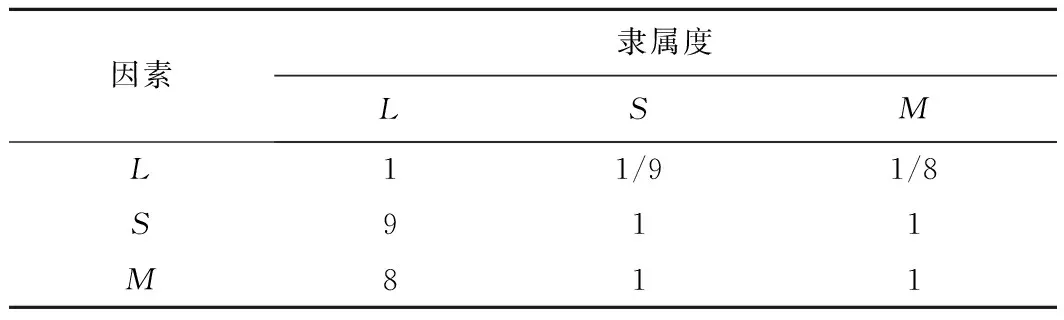
表4 双螺杆压缩机综合性能指标隶属度

由表4可知模糊判断矩阵

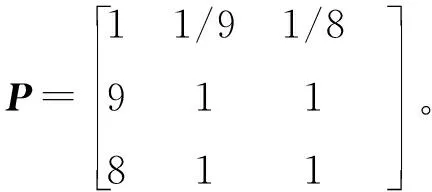
(15)

2) 求解特征向量

课题组在保证精度前提下，采用方根法求解其特征向量。首先计算N次方根

(16)

然后作归一化处理，其结果为：

(17)

将公式(17)的结果代入公式(11)，得到判断矩阵的最大特征根

λmax=3.001 5。

(18)

3) 一致性检验

已知最大特征根λmax=3.001 5，又m=n=3，根据已有的检验式(13)可得到判断矩阵的一般一致性指标

(19)

根据表3可知，当n=3时，RI=0.58。将CI和RI代入式(12)，得到：

CR=CI/RI=0.000 77/0.58=0.001 3≪0.10。

(20)

则符合要求K的关系式可表示成：

(21)

3.2 双螺杆压缩机综合性能分析

课题组用1条6次的NURBS拟合的复盛啮合线作为原始啮合线，然后对其进行优化设计，并重点计算每次调整前后的综合性能指标值[15]。

复盛啮合线作为一种典型的双螺杆压缩机型线，可以依照双螺杆压缩机转子型线计算公式计算得出M，S，L和K的值分别为0.454 2，4.258 8 mm2，148.146 0 mm和1.183 8。

同理，将啮合线划分为5个部分：AB，BC，CD，DE和EF。以AB段和DE段最高点H和J和EF段最低点P为界可将AB，DE和EF划分为左右2段，具体如图4所示。

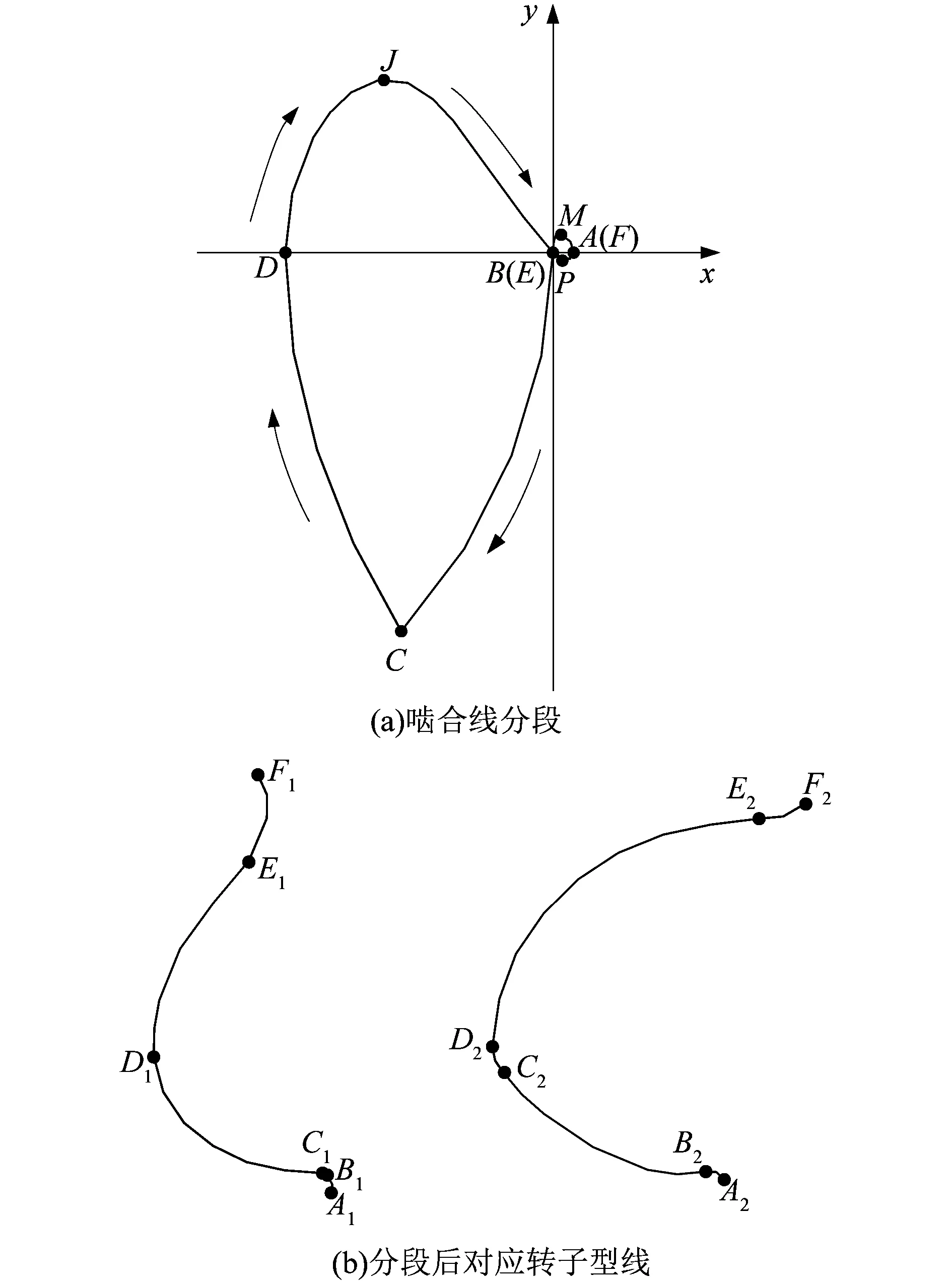
图4 啮合线分段及对应转子型线Figure 4 Meshing line segments and corresponding rotor profiles

然后将啮合线分段并将线段进行调整，分别计算得到如表5所示的接触线长度L，泄露三角形面积S，面积利用系数M以及综合性能指标K。

根据表5可知：

1) 当JE段向内调整时：L增大，S不变，M减小，这个结果是不期望看到的，且K=1.188 4>1.183 8。

2) 当JE段向外调整时：L减小，S不变，M增大，这个结果是期望看到的，且K=1.179 5<1.183 8。

3) 当PF向内调整时：L增大，S不变，M减小，这个结果是不期望看到的，且K=1.194 0>1.183 8。

4) 当HB段向内调整时：L增大，S增大，M几乎不变，这个结果是不期望看到的，且K=1.194 5>1.183 8。

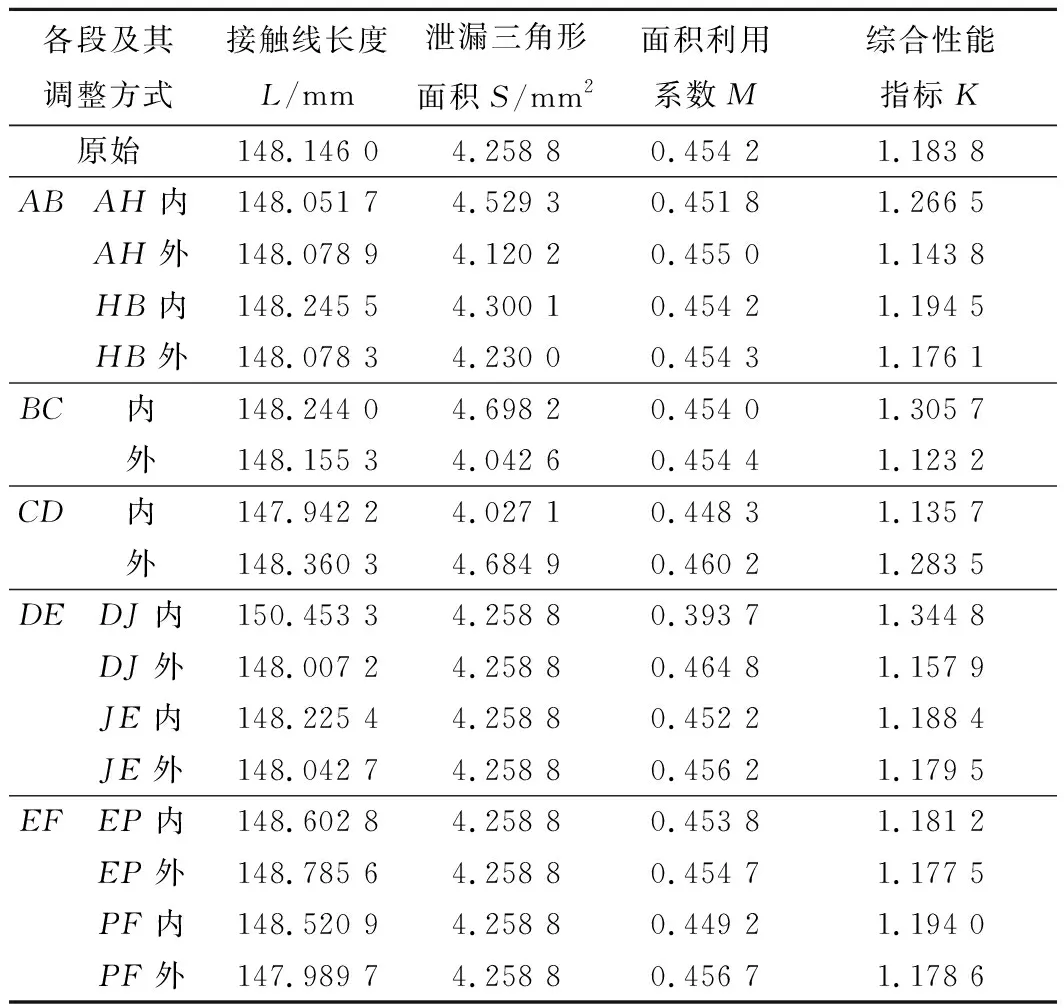
表5 啮合线各段调整对综合性能指标的影响

分析表5中数据可知：当啮合线往性能变好得方向调整时，综合性能指标K减小；往性能坏的方向调整时，K增大。

能够使型线性能向更好的方向发展的各段调整方式为：AH向外，HB向外，BC向外，CD向内，DJ向外，JE向外，EP不变，PF向外，详细调整的方向如图5所示。

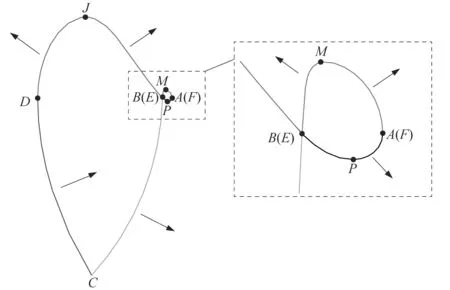
图5 啮合线各段优化方向Figure 5 Optimization direction of each section of meshing line

根据图5的调整方法，将表5中各段的优化调整后的各段型线整合成一条完整的啮合线，并根据该啮合线生成一条优化型线，原始型线与优化型线性能参数对比如表6所示。

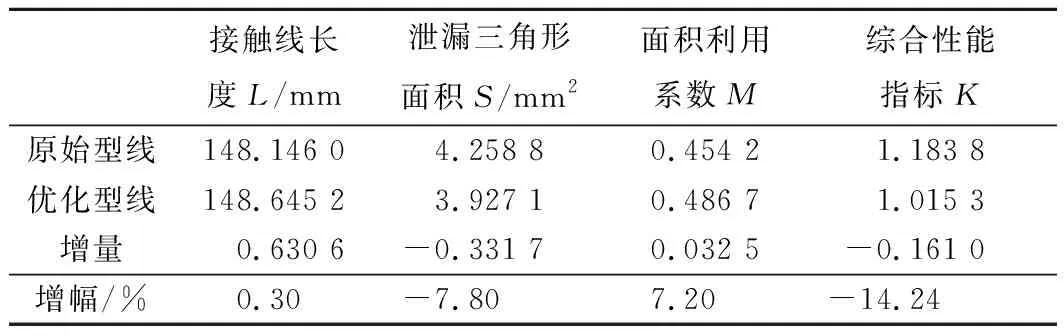
表6 原始型线与优化型线性能参数对比

由表6可知，与原始型线相比，优化型线的接触线长度略有增加，仅增加0.630 6 mm，相对增加了0.30%；泄露三角形区域面积减小了0.331 7 mm2，相对减小了7.80%；面积利用系数增大了0.032 5，相对增加了7.20%；综合性能指标相对降低了14.24%，即优化了14.24%，验证了综合性能指标表达式作用，能够有效的表征所设计转子型线经过优化之后性能指标的改变。

4 结论

针对双螺杆压缩机的性能评估中难以定量分析的问题，课题组提出了一种基于模糊综合评判法和层次分析法(FCE-AHP)的综合评估解析方法。首先分别对模糊综合评判法和层次分析法的基本原理以及计算步骤出了详细的说明；然后建立了双螺杆压缩机综合性能指标的评估体系，并分析了综合性能指标与各因素之间的关联性。接下来对比了几种常用的权重确定方法的优缺点以及适用情况，利用层次分析法分别求解了综合性能评估指标的权重，并基于多级模糊综合评判法得到了双螺杆压缩机综合性能指标K的表达式。最后，以1条6次拟合的复盛型线为例，计算其每次调整后的综合性能指标值，通过分析综合性能指标K来表征所设计转子型线优劣变化，证明了所求的综合性能表达式K可行性，避免了采用几何特性参数、热力学性能以及能效功率等方面作为对压缩机的整体性能的评判指标的片面性与效率低下等问题，对以后转子型线设计具有借鉴意义。

在后续研究中不仅应考虑最重要的因素，还应增加考虑其他有影响的因素，其中解决运算量较大的问题等尤需继续探索。