平面含复铰运动链拉普拉斯矩阵描述方法与同构判定

陈 诺， 孙 伟， 杨帆行， 胡高博， 潘宇航

(武汉科技大学 机械自动化学院， 湖北 武汉 430081)

机构综合的目的在于获得满足所有给定拓扑要求的可行机构构型，为机构的创新提供大量备选的结构方案，从而使设计者选择性能优异的新型机构用于机械装备的创新，并设计出具有优异性能的新型机械装备。机构综合需满足有效性，集成方法必须能够获得所有满足给定拓扑要求的可行机制。综合结果必须是完整、准确的，任何可行的机构都不能被遗漏。此外，集成机制必须合理，不包含具有相同拓扑结构的同构机制;然而，机构同构的确定一直是平面机构类型综合和优化中需要解决的难题。

对此，许多学者提出了相应的解决方案，罗玉峰等[1]提出关联度和关联度码的方法判定运动链的同构；聂松辉等[2]提出一种可以自动绘制运动链结构简图的最大环路法判定同构；孙晓斌等[3]提出了条件最大结构码及其求解方法，将问题降次为TSP问题进行同构判定；丁佳文等[4]提出了一种遍历环路的新型环路矩阵来描述行星轮系拓扑图的基本特征进行同构判定;孙伟等[5]提出构件邻接矩阵描述行星轮系拓扑图，并用改进哈明数的方法来进行同构判定；周豪等[6]提出加值矩阵结合特征向量的方法来进行同构判定；Rai等[7]提出一种简单的运动链构件标记算法，从而获得最大二进制序列码，用此作为一个结构恒量来判定同构；刘江南等[8]用转化邻接矩阵描述含复铰运动链，通过把复铰转换为单铰的方法来进行同构判定；伍星华等[9]提出了全等环路法，比较环路构件度从而判定是否同构；Manoj等[10]提出改进环联接方法，通过关节频率、链识别串等结构恒量来判定运动链是否同构；李安明等[11]通过判断特征码、和列阵2个结构恒量是否相等来判定运动链是否同构。综上所述，虽然复合铰链同构判定的方法甚多，但有些方法存在着不适合运算，运算量大，及转化复杂等问题。

故课题组提出了一种简单而精确的同构确定方法，并引入了由邻接矩阵和度矩阵组成的Laplace矩阵来描述运动链，特别是包含复合铰链的运动链。将拉普拉斯矩阵进行SVD分解后的奇异值向量作为确定的必要条件。通过对大量的案例进行论证，表明该方法具有准确性和高效性。

1 拉普拉斯矩阵的构建

1.1 拉普拉斯矩阵的定义

将度矩阵和邻接矩阵用于构造拉普拉斯矩阵，即

L=A-D。

(1)

式中：L为拉普拉斯矩阵，是一个n阶的方阵，其中n由运动链杆件数决定；A为邻接矩阵;D为度矩阵。

A需要考虑相邻分量之间的关系，D需要考虑一个拉普拉斯矩阵在度或度上的元素，即顶点连接的分量的数量。矩阵的行和列是运动链的联数，包含复铰和移动副的矩阵元素。

含复铰的矩阵元素计算公式：

(2)

式中:i和j表示关节编号，数值根据构件的情况取值0或1，相邻的构件含复铰取1，构件不相邻数值为0；deg (vi)表示顶点vi的度，数值取决于构件的连接数目。

含移动副的矩阵元素计算公式：

(3)

式中:i和j表示关节编号，数值根据构件的情况取值为0或2，相邻的构件含有移动副取2，构件不相邻数值为0；deg (vi)表示顶点vi的度，数值取决于构件的连接数目。

1.2 拉普拉斯矩阵的实例

图1所示为一个含复铰的10杆运动链。

图1 运动链a1的结构简图Figure 1 Structure diagram of kinematic chain a1

拉普拉斯矩阵L的元素lij(i≠j)表示运动链a1构件i和构件j之间的连接关系。例如：元素l12=1，表示构件1和构件2之间有连接；元素l13=0，表示构件1和构件3之间没有连接。元素lii表示运动链a1构件i连接构件的数目。例如，l11=-4，表示构件1处连接有4个构件。

可通过拉普拉斯矩阵来求解奇异值，由LL*的特征值取平方根获得。依据

|λE-LL*|=0，

可求出特征值。

其中：λ是拉普拉斯矩阵的特征值，E是单位矩阵。

求出特征值后，奇异值可由特征值取平方根获得，结果用一组列向量表示。

(4)

2 同构判定

由相关理论及同构的概念可知，要使2个运动链同构，必须含有相同的构件种类、构件数量、构件连接关系。对于构件之间的连接关系，构件数量均已确认相同。在进行同构判定时，首先构建出拉普拉斯矩阵，由拉普拉斯矩阵的性质可知拉普拉斯矩阵每一行、列求和均为0，则0是奇异值向量中的一个元素，可以检测拉普拉斯矩阵的正确性，然后用奇异值分解(singular value decomposition,SVD)求出奇异值向量，比较2个运动链的奇异值向量，若相等则运动链同构，否则不同构。

图2所示为2个具有复杂铰链的10杆运动链，可以构建出各自的拉普拉斯矩阵并求得奇异值向量。运动链a2,a3的拉普拉斯矩阵和奇异值向量的结果如下:

(5)

(6)

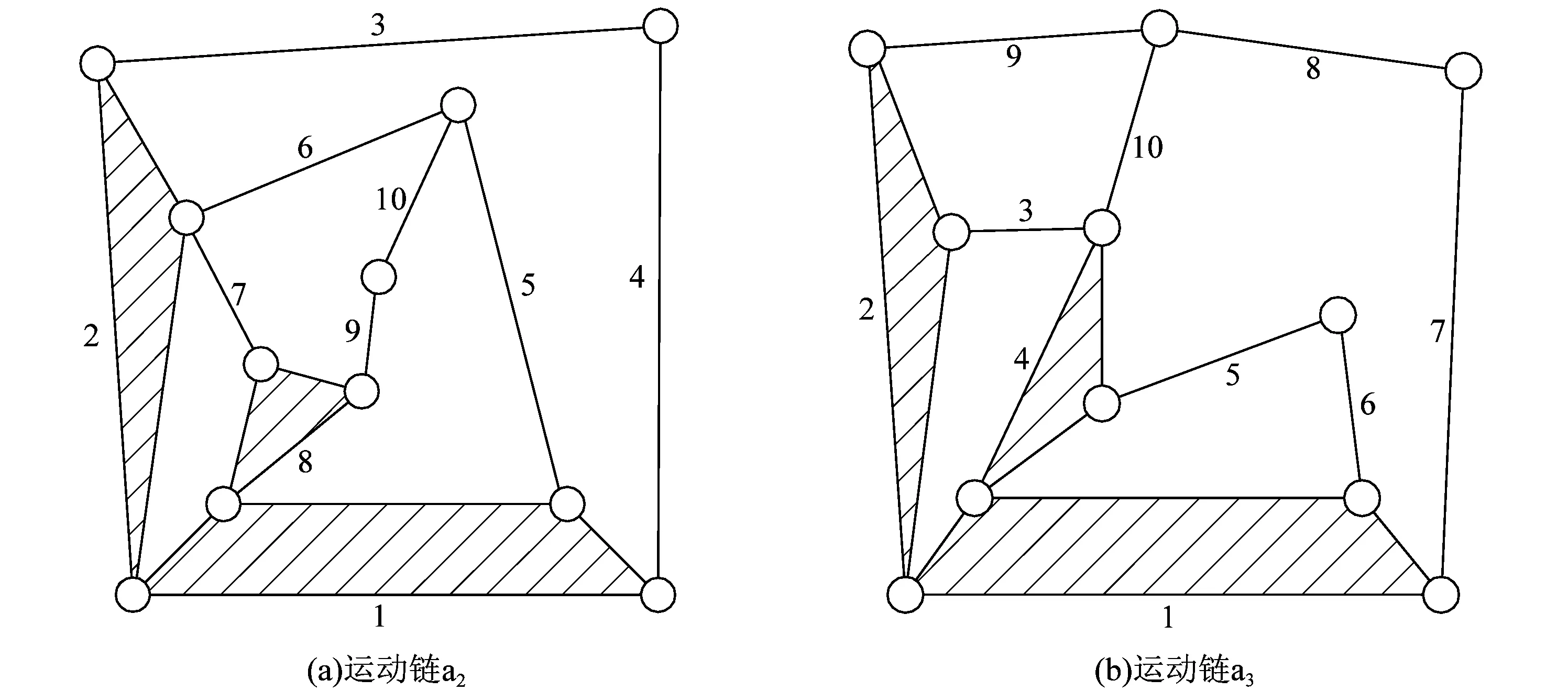
图2 运动链a2和a3的结构简图Figure 2 Structure diagram of kinematic chain a2 and a3

由结果可以看出，奇异值向量中含有元素0，符合拉普拉斯矩阵性质，对比奇异值向量的结果显示Sa1=Sa2≠Sa3，所以运动链a1和a2是同构运动链，运动链a3是异构。

3 案例分析

3.1 含复铰的运动链

图3所示为2个13杆含复铰运动链结构简图。

图3 运动链a13和b13的结构简图Figure 3 Structural sketches of kinematic chains a13 and b13

求出了该运动链的拉普拉斯矩阵和各个矩阵的奇异值向量为：

(7)

(8)

由式(7)和(8)可知，奇异值向量中含有0向量，则说明与拉普拉斯矩阵的性质符合，对比奇异值向量的结果显示Sa13≠Sb13，因此，运动链a13和b13是异构。

3.2 含移动副的运动链

拉普拉斯矩阵不仅可以描述和判断包含复杂铰链运动链的平面的分量，还可以判断包含移动副的运动链。在邻接矩阵和度矩阵中，移动副的权重为2。图4所示的虚线部分表示移动副。

图4 含移动副的10杆运动链Figure 4 10-bar moving chain with moving pair

含有移动副的10杆运动链的拉普拉斯矩阵和每个矩阵的奇异值向量：

(9)

(10)

(11)

由式(9)～(11)可知，该含有移动副的10杆运动链所形成拉普拉斯矩阵的奇异值向量中含有元素0，符合拉普拉斯矩阵的性质，对比奇异值向量的结果显示Sg1=Sg2≠Sg3，可得知运动链g1与g2是同构，g3是异构。

4 结语

课题组提出了拉普拉斯矩阵来描述具有平面复杂铰链的运动链。构建的拉普拉斯矩阵实现矩阵与运动学链的一一对应。该矩阵可以通过SVD进行分解，得到的奇异值向量可以判断运动链的唯一性，0元素可以检验矩阵的正确性。该方法不仅可以用于包含复杂运动链的同构判定，还可以用于包含移动副的平面运动链同构判定。实例证实了该方法的有效性和高效性。相比其它判定法，该方法的矩阵简洁美观，可读性强，且用SVD分解得到结果较为准确、快速。