基于GA优化的SVR对膛线切削力的预测

刘 洋，关世玺，赵 宏，沙业典

(1.中北大学 机电工程学院，太原 030051; 2.晋西工业集团有限责任公司，太原 030027)

1 引言

用智能算法解决火炮膛线切削力预测问题具有“简单、快捷且精度高、成本低”等优点。随着火炮制造技术的不断发展，火炮膛线加工刀具的制造便有了更高的要求。其理论设计及后续的实际加工都需要以大量的切削力数值为依据，但火炮膛线加工领域缺少适合的智能预测算法。因此，寻找一个适合膛线加工的预测算法便显得尤为关键。目前在膛线切削领域常用的预测算法有“BP神经网络”、“支持向量机”、“曲面响应法”、“Kriging”、“多元回归”等算法。Vaishnav S、王俊成、陈远玲等学者使用BP神经网络较好地预测了切削力。白冰、单晓敏等学者使用支持向量机预测了切削力，并得到了精度较高的结果。向莹和张祺等学者使用Kriging算法对切削力进行了预测。赵庆、袁人炜等学者用响应曲面法对切削力进行了预测。Jurkovic Z 比较了神经网络、支持向量机和多项式回归3种预测方法在切削加工中的性能。

用“多元回归”的方式预测切削力虽然简单、常规，但其预测精度有待提高，且在智能化方面的优势不足。曲面响应法虽然在预测精度方面有一定程度的保证，但其在智能化方面的优势不明显。神经网络虽然具有强大的学习能力，但其网络结构复杂、较难优化，且存在过拟合、易陷入局部最优和泛化能力较差等问题。支持向量机虽然拥有预测精度高、学习能力强和高泛化能力等优点，但其在实际运用中的参数设置问题是无法忽略的难点。基于这个难点，采用遗传算法对支持向量机进行参数寻优，并最终获得预测精度较高的切削力预测值。

2 膛线加工仿真以及切削力预测

2.1 膛线加工仿真

首先在三维建模软件中建立刀具、工件的几何模型；随后将其导入Abaqus中进行切削仿真。Abaqus仿真操作过程如下：

1) 在材料模块中，将刀具设置为刚体，工件材料以42CrMo为例；刀具材料参数如表1所示。

表1 刀具材料参数Table 1 Tool material settings

2) 在step模块中，建立3个Step(initia、Step1、Step2)，并将其设置为“动力，温度-位移，显示”，即采用力热耦合模式；

3) 在相互作用模块中，设置摩擦系数为0.2，并设置刀具-工件的相对运动；

4) 在边界条件模块，initial中设置边界条件，将身管固定,即将远离切削的身管端面设置为完全固定(ENCASTRE)；Step1中设置刀具旋转角度；Step2中设置刀具进给速度；

5) 在网格模块中，设置网格属性为六面体-扫略-中性轴算法网格；单元类型选取“温度-位移耦合”；网格划分采用局部-整体结合的方式：网格全局种子设为0.20 mm，对身管内表面进行局部细化，采用局部种子单精度偏移法，越靠近接触面加工区域，网格越精细，细化网格设置为 0.1～0.4。

6) 提交job

仿真效果，如图1所示。其中，刀具采用(前角=1402°、后角=7°、左副偏角=49°、右副偏角= 5°)切削速度设置为1～10 m/min，相邻间隔为0.2 m/min；切削深度设置为0.1～1 mm，相邻间隔为0.1 mm。通过对切削参数进行正交试验得出对应的切削力，并在Matlab将其归一化，如表2所示。

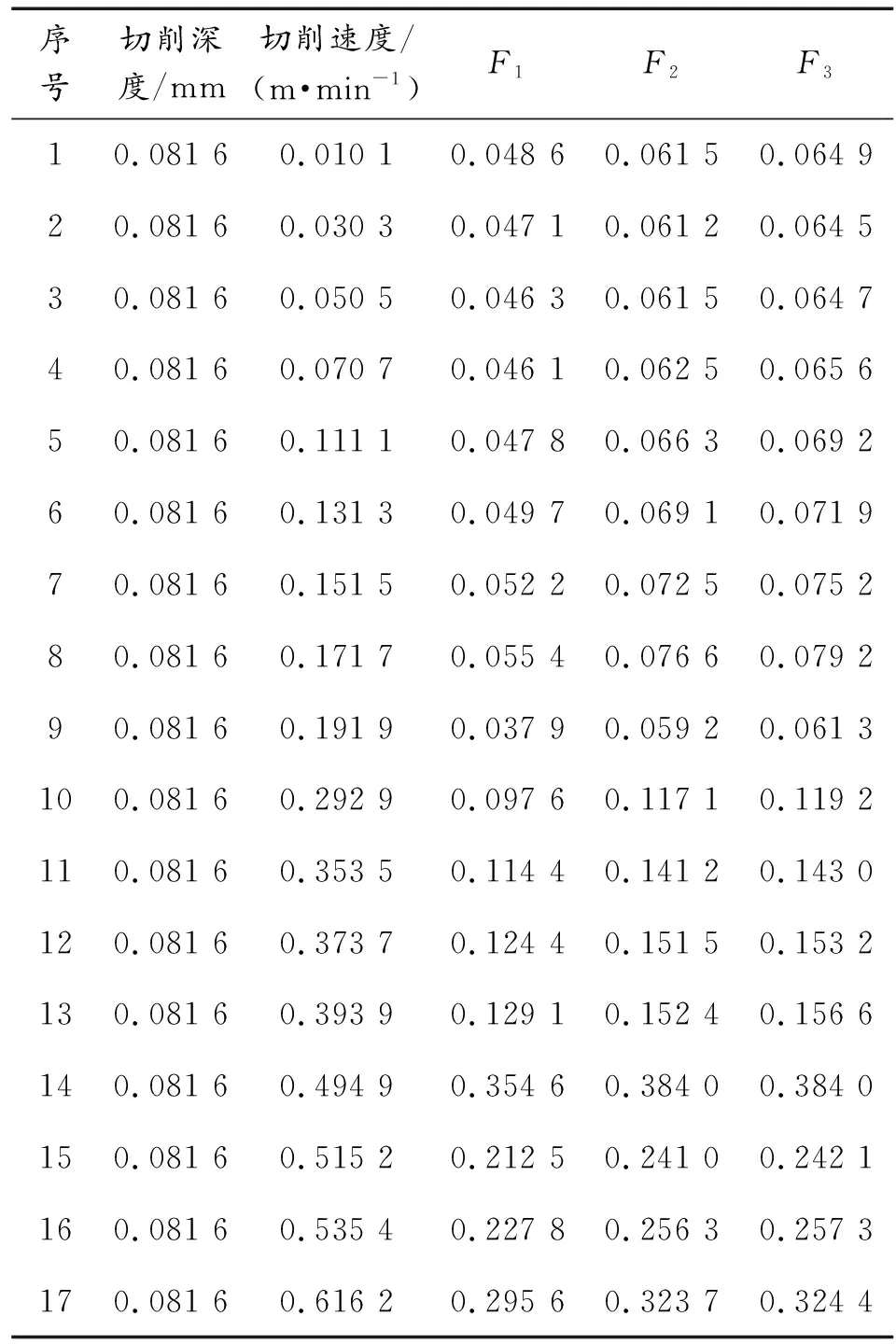
表2 归一化后的数据(限于篇幅只展示部分数据)Table 2 Normalized data (due to space,only some data are shown)

图1 仿真效果图Fig.1 Simulation effect

2.2 基于切削参数的切削力预测

切削力的预测方式有很多种，文献[10]中通过刀具几何参数预测切削力；文献[1]中通过轴向切深、主轴转速、进给量和曲面半径预测了切削力;为了在保证精度的前提下简化预测模型，且由切削力经验公式可知，切削力的主要影响因素为切削深度以及切削速度。由此本文采用切削参数(切削深度、切削速度)预测切削力。模型训练过程如图2所示。

图2 模型训练过程框图Fig.2 Model training process

3 基于遗传算法优化的支持向量回归机的基本原理

3.1 遗传算法

遗传算法的核心原理是引入自然生物界优胜劣汰的进化法则，通过迭代得到理想的全局最优解，其在优化问题的求解上有独特的优势，且应用简单，计算高效。本文采用的是较为常规的遗传算法，基本过程包括：“选择—交叉—变异—精英选择”。

算法的步骤如下：

1 个体编码

采用二进制编码机制，即将实数解转化为二进制形式，经过一系列遗传操作之后再从二进制形式转化为实数形式。考虑到算法运行的时间复杂度，其编码位数需要适当选择。本文中共4个优化参数(4个变量)，每个参数赋予10个位数，由此本文二进制解的位数总和为40。

2 赌轮选择

采用“轮盘赌”的选择方式选择优秀的个体并保留至下一代。

3 两点交叉

采用的交叉操作为个体间相互交叉。步骤如下：

1) 设置交叉概率；

2) 在[0,1]中生成随机数，若<，则个体发生交叉操作；

3) 在[0,1]中生成随机整数，若=1，则将第个个体基因中所有值为1的位置与第+1个个体在该位置的基因互换；

交叉操作示意图如图3。

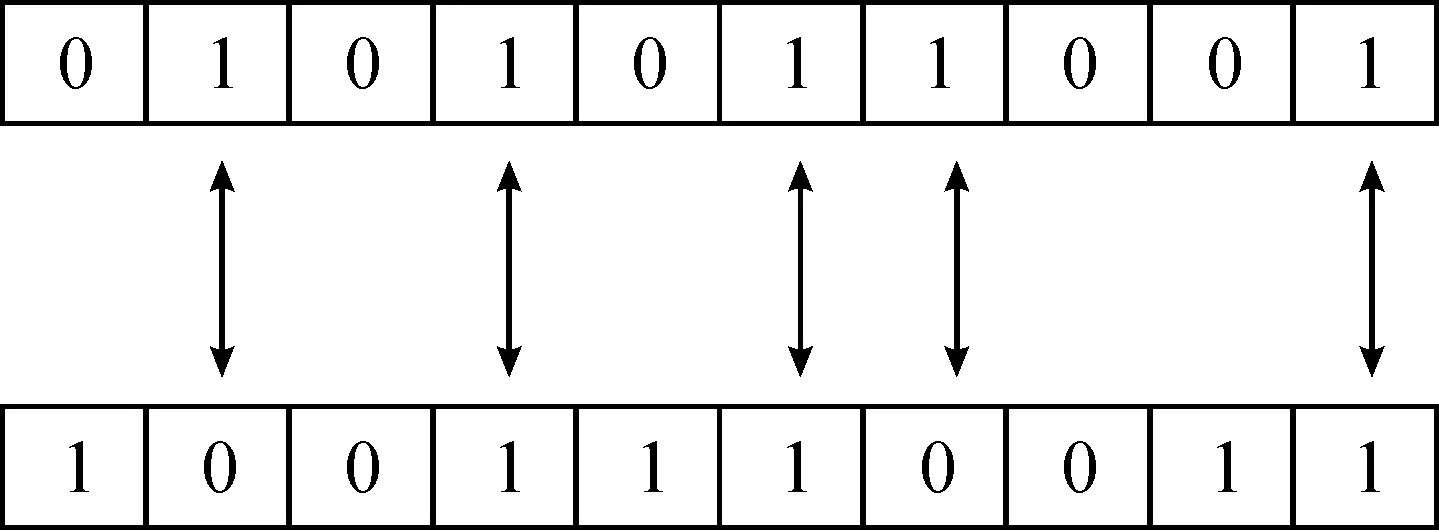
图3 遗传算法交叉操作示意图Fig.3 Genetic algorithm crossover operation

4 变异

由于交叉操作是通过随机的方式产生操作点，子代极有可能不是期望解，故可通过变异操作增加其成为期望解的概率。

5 精英保留

在产生的子代种群中，选出适应度最高的个体与当前最优个体(精英)进行比较，适应度较高的成为新的最优个体(精英)。

3.2 支持向量回归机

已知支持向量机回归的原始最优化问题为：

(1)

s.t. (·)+-≤,=1,…,

(2)

-(·)-≤,=1,…,

(3)

经过对偶处理并将线性硬-带支持向量机回归“软化”，便可得到线性-支持向量机回归。后得最优化问题为：

(4)

s.t. ((·)+))-≤+,=1,…,

(5)

(6)

(7)

上述便是基于线性-支持向量机回归的原始问题的凸二次规划。

(8)

3.3 遗传算法优化的支持向量回归机的实现

遗传算法优化支持向量回归机可在Matlab中实现，具体步骤如下：

1) 将遗传算法中的适应度函数替换为支持向量回归机主函数；

2) 将支持向量回归机的4个参数惩罚系数、epsilon-SVR的损失函数、允许的终止判据、函数等设置为遗传算法中对应的输入变量；

3) 将预测误差作为遗传算法适应度函数的返回值；

4) 设置遗传算法的种群个数，迭代次数，交叉概率，变异概率；

5) 运行程序；

经过遗传算法多次迭代最终可得最优适应度函数值(误差最小值)，以及误差值最小情况下的最优参数。如图4所示。

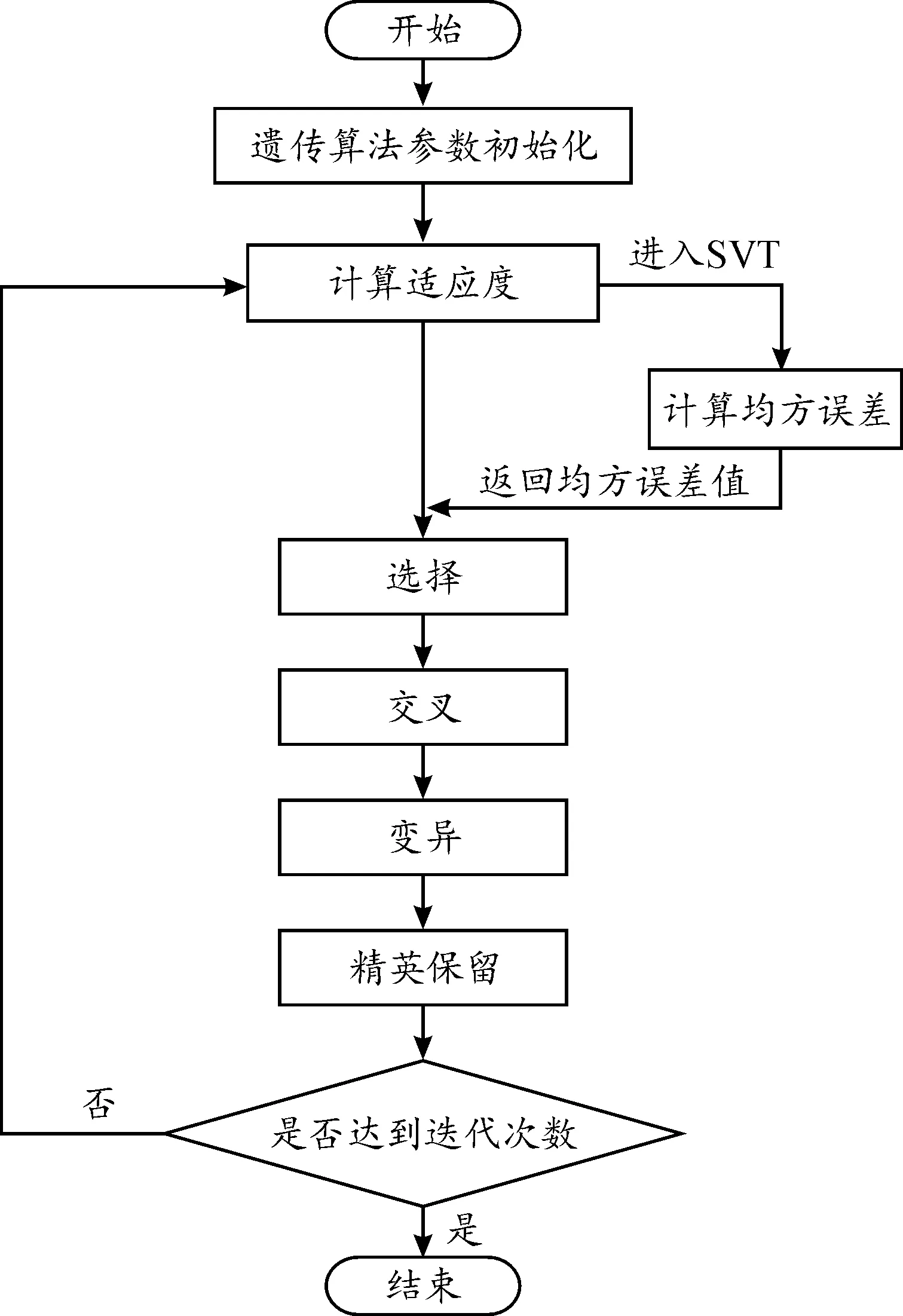
图4 算法基本流程框图Fig.4 Basic flow of algorithm

4 切削力预测仿真

通过上述预测模型进行切削力预测，具体步骤如下：

1) 利用Matlab中的mapminmax函数对数据进行预处理，即在区间[0,1]中归一化；

2) 将归一化后的数据进行分组，分为训练组和测试组；

3) 将训练组数据代入模型中进行训练；

4) 用训练之后的模型进行预测，并用测试组数据算得相应的预测误差；

5) 经过多次迭代，选择预测误差最小的支持向量回归机参数；

6) 导出该最优参数下的切削力预测值；

遗传算法参数设置如表3所示。

表3 遗传算法参数Table 3 Parameters of genetic algorithm

通过上述操作得出预测精度(均方误差)以及该模型对应的最优参数见表4所示。

表4 预测精度以及最优参数Table 4 Prediction accuracy and optimal parameters

从表4中可提取优化前后均方误差值进行优化精度评估，即：

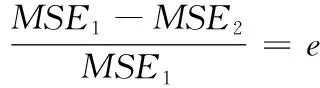
(9)

其中:为优化前的均方误差；为优化后的均方误差；为优化前后均方误差的降低比率(预测精度提高率)。

利用式(9)可分别得出、、的预测精度提高率分别为6613、5704、5828。

最优参数对应的切削力预测值如表5所示。

表5 切削力预测值Table 5 Predictive value of cutting force

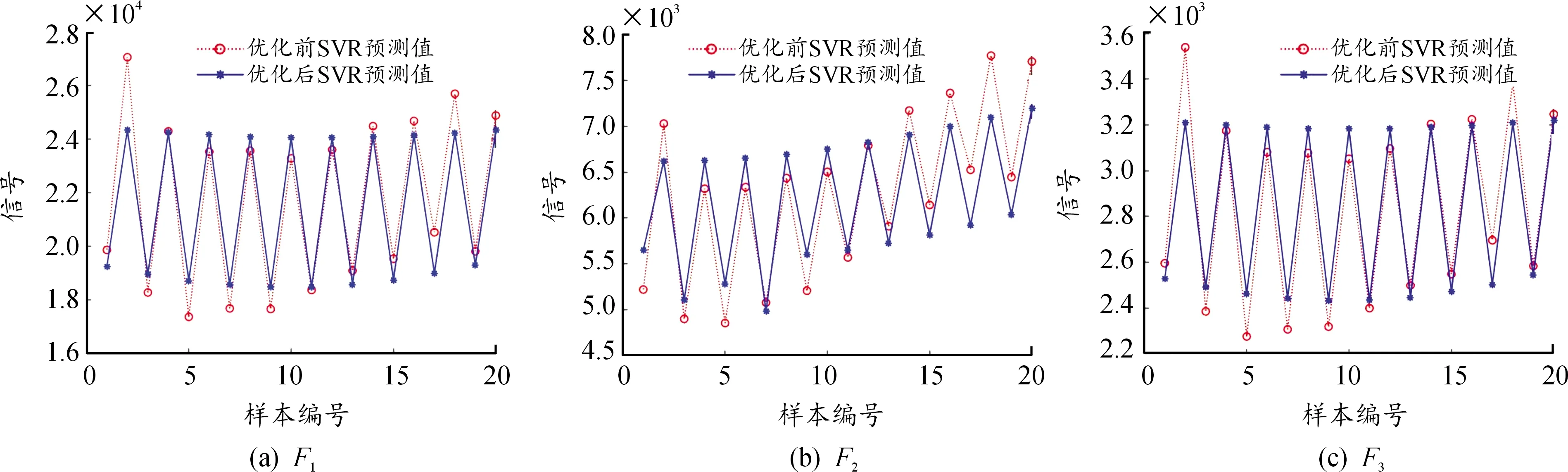
图5 仿真值与预测值曲线Fig.5 Comparison of simulated and predicted values

5 验证

本切削力实验通过测力仪、机床、计算机等仪器进行。其中机床采用MV-1270数控铣床；测力仪为YDX系列。如图6所示，为力求有限元仿真与实验过程的一致性，实验刀具和工件的形状、材料以及加工过程与有限元仿真相近。

图6 切削力实验用机床和测力仪实物图Fig.6 Cutting force test

通过对测试组中的切削参数进行正交试验得出对应的切削力，实验过程如图7所示。

图7 实验过程框图Fig.7 Simulation diagram of experimental process

具体实验步骤如下：

1) 对毛坯表面进行加工处理，使其能够满足实验条件；

2) 清理数控机床工作台面、测力仪和工件，避免遗留的切屑影响到切削力信号的采集工作；

3) 安装测力仪，此过程中应注意对基准面进行找正，尽可能减小安装误差；

4) 安装、固定机床刀具以及工件，并对测力仪等测量装置进行检测；

5) 实验前进行一次试切，既能检查各个装置的连接情况，也便于对刀；

6) 进行实验，为了避免零漂现象对信号采集产生影响，须在刀具切入切出前后选取空切时段进行信号采集。

7) 测量完成后对电荷放大器进行复位操作；

8) 改变实验切削参数，重复6)～8)； 选择长度为1 000 mm的毛坯，通过设置各种切削参数，可得如表6所示的数据。

表6 实验值Table 6 Experimental values

由表5可看出火炮膛线切削力预测值与实验值接近，其数值如图8所示。

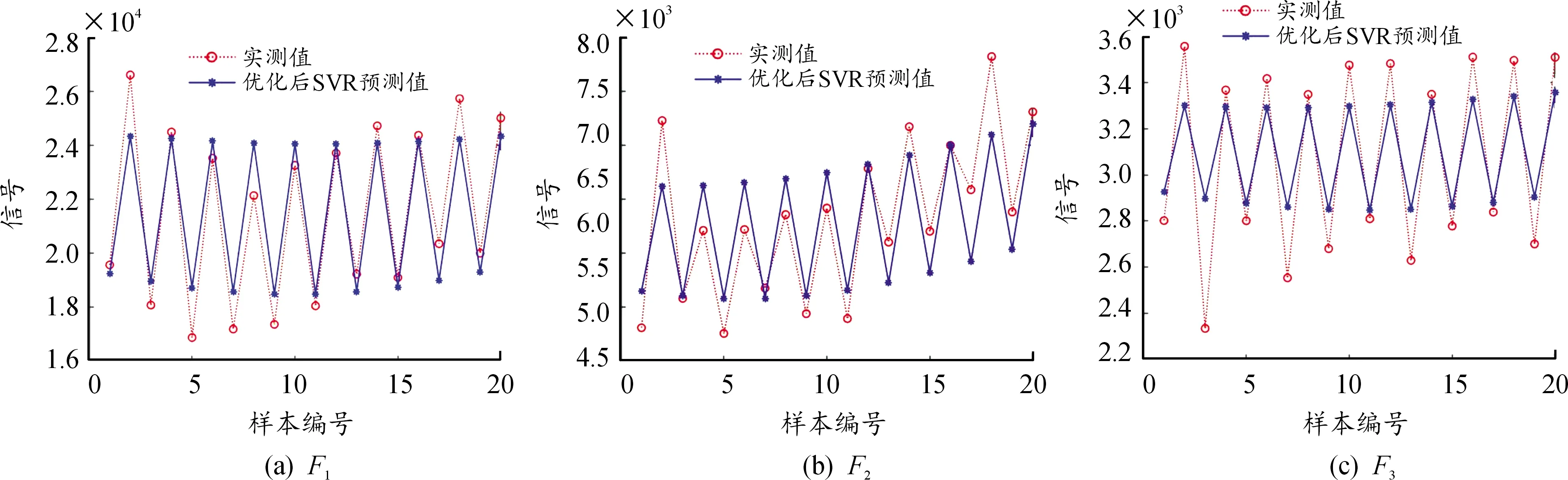
图8 数值曲线Fig.8 Curve of numerical comparison

6 结论

1) 遗传算法优化的支持向量回归机模型能够对火炮膛线切削力进行预测；

2) 该模型在“膛线加工”中具有良好的预测效果，相较于优化前的支持向量回归机，其预测精度均提高55%以上；

3) 该算法得出的预测值与实测值大致吻合。随着机械加工领域中的智能化趋势越发明显，切削力预测将得到更多学者关注。