基于RBF-SVR组合模型的切削力预测

于洋，王关，贾智旗，任玉斌

西安科技大学机械工程学院

1 引言

机械加工时产生的切削力在一定程度上影响着刀具磨损以及产品的加工质量，准确预测切削力不仅能更好地判断刀具磨损状态、提高工件加工精度，还能为确定加工参数提供依据，从而保证工件加工质量，提高生产效率[1]。所以精准预测切削力对实际生产起着关键作用。

切削力与其关键影响因素之间的数学关系较为复杂，难以建立精准的切削力预测模型，为提高其预测精度，研究人员提出了一些预测方法。胡艳娟等[2]采用模糊线性模型预测切削力，得到在一个可变区间波动的不确定值，对预测切削力有很大的参考价值。白冰[3]用支持向量机回归模型选择四个关键参数为输入参数对切削力进行预测，结果表明，分析非线性小样本数据时，SVR有较大优势，能很好地对数据进行可靠性评估。张臣等[4]根据BP网络模型预测铣削力，并考虑了较多影响因素，发现其对切削力的影响能以网络结构参数映射到铣削力的预测值中。郑金兴[5]提出用PSO算法优化BP网络寻参过程，研究发现，相比于标准BP算法，收敛速度和精度均有所提高。李康等[6]结合经验公式模型与其他模型预测切削力，证明了组合模型比单一模型的泛化性更好且精度更高。翟元盛等[7]利用遗传算法建立插铣切削力的预测模型，结果表明，切削力预测值与实验值吻合度较好。

上述研究的模型大多为单一预测模型或预测精度还可优化的组合模型。单一模型在预测时考虑的信息不够全面，如文献[6]中的经验公式模型用最小二乘法进行参数估计，但忽略了一部分难以量化的因素，致使切削力预测值和真实值之间差值过大；文献[4]提到的BP神经网络模型存在学习速度慢和容易陷入局部最小点而不能得到最优结果等问题。针对预测切削力的数据较少且输入参数和输出参数之间呈复杂非线性关系的特点，本文用RBF神经网络和支持向量机回归两种算法预测切削力，再用最优加权法确定权重系数，构建组合预测模型，提高切削力预测精度和泛化性。

2 模型介绍

2.1 RBF神经网络预测模型

RBF神经网络是一种具有单隐含层的前向网络，有研究者论证了RBF神经网络对非线性连续函数的一致逼近性能[8]也能进行预测。用RBF作为隐单元的“基”构成隐藏层空间，其隐含层神经元激励函数一般为高斯核函数，有

(1)

式中，‖x-ci‖为样本x到中心点ci的距离；ci为隐含层第i个神经元的中心向量；σi为隐含层第i个神经元的宽度向量。

输出层神经元的输出为

(2)

式中，w为调节权重；q为输出层单元数。

将切削三要素作为网络的输入节点，对数据归一化，使其成为无量纲数值，确定newrb函数中的spread值及核函数参数等，以创建网络。

2.2 支持向量回归预测模型

支持向量回归(SVR)是指在对切削力的数据进行拟合时，采用支持向量机(SVM)的原理对数据做非线性回归分析的方法。

设在高维特征空间中建立的线性回归函数为[9]为

f(x)=wΦ(x)+b

(3)

式中，Φ(x)为非线性映射函数；b为偏置项。

(4)

式中，K(xi，x)为高斯径向基核函数；x为切削力训练样本。

在进行切削力预测时需确定惩罚因子，以及选择损失函数和核函数的参数等。

3 组合预测模型

组合预测模型的原理是通过一定的数学方法，对不同的单一切削力模型进行组合，充分利用单一模型算法的优势，取长补短，得到新切削力组合预测模型。实验与仿真分析证明，预测切削力时，组合模型的预测效果更好。构建组合预测模型的核心为估计权系数，采用最优加权法处理预测值，并采用以下方法计算确定加权系数[6]。

最优权值矩阵W*可表示为

(5)

式中，S为预测误差信息矩阵；W*为使所需的t个单一预测模型进行组合的权系数向量，W*=[W1，W2，…，Wt]T，且满足式(6)；I1=[1，1，…，1]T。

(6)

式中，t为单一预测模型个数。

本文采用算术平均法建立组合模型，组合模型预测值的计算式为

(7)

式中，YC为组合模型预测向量。

组合模型构建流程如图1所示。

图1 组合模型构建流程

4 实验验证与仿真分析

4.1 实验材料与方法

本文引用文献[10]中微车削钛合金时的切削力真实值验证预测模型的可信性。工件材料为TC4钛合金，直径7mm，长度100mm，刀具参数如表1所示，部分切削数据如表2所示。

表1 刀具参数

表2 切削力实测值

4.2 模型预测结果与分析

4.2.1 RBF神经网络预测模型

根据MATLAB软件中的newrb函数创建RBF网络，利用表2中前22组切削力训练集数据训练RBF网络模型，其中newrb函数中径向基函数扩展系数spread经过调试后确定为10。将23～27组测试数据输入神经网络模型中，最终得到切削力预测值YR。图2为切削力真实值与预测值的对比折线图，两者趋势基本吻合。

图2 真实值与RBF预测值对比

图3为切削力相对误差，其切削力预测值中相对误差绝对值的最大值为0.059，最小值为0.004，均值为0.035，说明RBF网络模型预测切削力的精度高、稳定性较好。

4.2.2 支持向量回归预测模型

通过MATLAB中的工具箱libsvm构建SVR预测模型。利用前22组切削力训练集数据训练SVR模型，核函数为高斯径向基函数，通过交叉验证法对参数寻优后有：C=1684，σ=2.293。将最后5组切削力测试数据输入模型中，得到预测值YS。图4为切削力真实值与预测值的对比折线图，两者趋势基本吻合。

图3 切削力相对误差

图5为切削力相对误差，其中切削力预测值中相对误差绝对值的最大值为0.058，最小值为0.036，均值为0.0457，总体来看，SVR模型的泛化性能优于RBF网络模型，但预测精度略低。

图5 切削力相对误差

4.2.3 组合预测模型

RBF神经网络和SVR模型预测值如表3所示。由表中所示切削力真实值和预测值，计算得到预测误差信息矩阵S为

(8)

式中，e为测试误差矩阵，即真实值与预测值的差值。

表3 两种单一模型预测值

将式(8)代入式(5)，得出最优权值向量为

(9)

则组合模型可以表示为

YR-S=0.584YR+0.416YS

(10)

将第23～27组测试数据输入RBF-SVM组合模型中，得到预测值YR-S。图6为切削力真实值与预测值的对比折线图，两者趋势基本吻合。

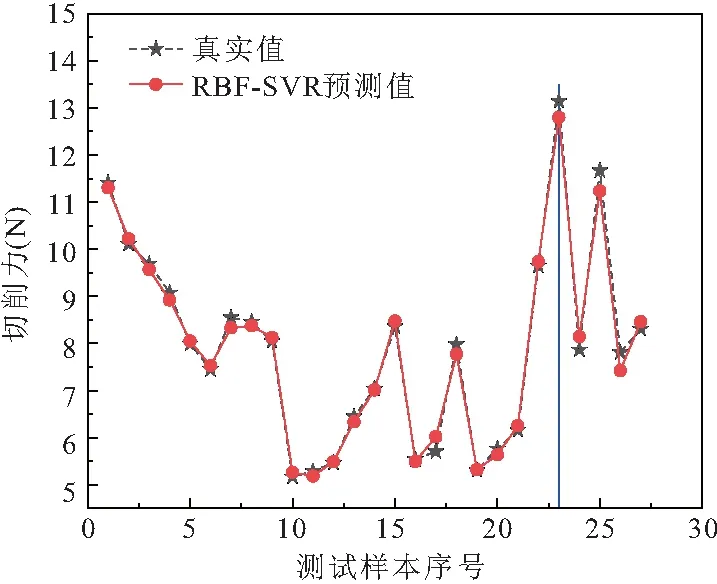
图6 真实值与组合模型预测值对比

图7为切削力相对误差，其中，切削力预测值中的相对误差绝对值的最大值为0.050，最小值为0.018，均值为0.033。与上述单一预测模型对比，除第5组数据预测值外，其余组预测值的相对误差均有所降低，且相对误差绝对值的平均误差更低，说明组合模型的误差波动范围小，预测精度较高。

图7 切削力相对误差

4.3 预测结果误差分析

本文采取以下三种误差指标评价预测模型，数值越小表明预测效果越好[11]。

平均绝对百分比误差为

(11)

平均绝对误差为

(12)

均方根误差为

(13)

式中，N为测试预测模型所需样本数；yi为切削力预测值；fi为切削力真实值。

将最后5组切削力真实值和三种模型预测值分别代入式(11)～式(13)中，计算三种误差指标，结果如表4所示。

表4 预测模型误差评价指标对比

表中，预测方法YE和YAGEM分别为文献[6]中的经验公式模型和组合预测模型(AGEM)，该组合模型是基于人工神经网络、高斯过程回归模型和经验公式构建的。本文与文献[6]的切削力数据皆引自于文献[9]，在使用相同切削力数据的前提下，可以更好地将本文预测结果方法与其他方法做对比，体现本文方法的优势。

表4中RBF-SVR组合模型的3个评价指标几乎都小于RBF神经网络模型和SVR模型，表明相较于单一模型，由组合模型得到的切削力预测值与真实值整体偏离较小，预测精度和泛化性较高。而RBF-SVR和AGEM组合模型相比，三种误差评价指标分别降低50.86%，40.63%，40.89%。

5 结语

实际加工中，由于切削力影响因素很多，建立预测模型时应尽可能考虑多种因素及合适方法，以保证模型预测精度。以切削三要素为关键因素，通过合理组合建立具有较强非线性拟合能力的模型，并运用新模型预测切削力，得到以下结论。

(1)以最优加权法确定RBF网络和SVR模型权重系数，采用算术平均法构建组合预测模型。分析结果表明，相对于单一模型，RBF-SVR组合模型的预测精度有明显提升且稳定性较好。

(2)在分析相同切削力数据的前提下，RBF-SVR组合模型的三种误差评价指标均小于AGEM组合模型，说明该模型能更准确地预测切削力的变化，且不同单一模型对组合模型的预测精度有很大影响。

(3)通过分析RBF神经网络和SVR建立的单一模型可知，RBF神经网络模型的误差评价指标小于SVR模型，具有更好的非线性拟合能力以及预测效果。