脊形前体飞行器静态绕流数值模拟研究

司芳芳，袁先旭，贺旭照，谢昱飞，叶友达

(1.北京流体动力科学研究中心， 北京 100120；2.中国空气动力研究与发展中心， 四川 绵阳 621000)

1 引言

未来战斗机需要大幅度提升空战性能，目前先进战斗机如F-22和F-35均采用脊形前体，以降低可探测性和提升空战性能。脊形前体主要是由切拱弧和脊形边缘组成。攻角变化时，脊形边缘使得背风流场的分离点固定，与尖前缘高后掠三角翼的流场十分相似。脊形前体高度混合外形良好的隐身性能和超声速飞行性能使其成为未来高性能战斗机和巡航导弹比较理想的前体布局形式。

与具有光滑前体的传统战机相比，脊形前体通常会产生更强的前体涡流。某些特定飞行条件下，脊形前体产生的前体涡与机翼的前缘涡以及飞机其他结构之间存在强干扰，所以国外研究人员对脊形前体、三角翼等结构之间的涡干扰进行了大量的试验研究。目前，脊形前体数值模拟方面的研究主要有Ravi和Mason等用欧拉方程和雷诺方程数值模拟研究了大攻角、有侧滑情况下脊形前体的方向稳定性。Agosta-Greenman等用薄边界层雷诺平均纳维-斯托克斯方程(navier-stokes equations,N-S方程)数值模拟了切向吹气对脊形前体气动力的影响。在20世纪90年代中期，美国国家航空航天局兰利研究中心、洛克希德·沃斯堡公司、洛克希德·马丁公司和波音公司都致力于用欧拉数值模拟方法来研究中高攻角时脊形前体类飞机的气动力特性，一致的结论是欧拉解对飞机的初期设计有一定的指导意义，虽然欧拉方程可以准确的模拟主涡结构，但是不能研究由粘性产生的二次涡和三次涡以及分离涡的粘性干扰等非线性情况，所以只有采用湍流三维N-S方程来模拟非定常分离涡，以及前体涡与机翼涡之间的干扰等现象。Jeans等采用DDES(delayed detached-eddy simulation)湍流模型数值模拟研究了脊形前体类简化飞机模型的大攻角非定常以及动态滚转现象，模拟出了试验中的非线性气动力。

尽管已进行大量工作，但由于脊形前体大攻角非定常大范围湍流分离流的复杂性，目前对脊形前体飞行器的大攻角流动机理认识尚不充分，深入了解其大攻角气动特性，尤其是脊形前体与翼型相互干扰的气动特性有着重要的工程应用价值以及学术意义。

针对脊形前体类飞行器大攻角非定常湍流大分离流动特点，本文采用IDDES(improved delayed detached-eddy simulation)方法来研究脊形角7.5°的前体添加平板机翼组成的脊形前体飞行器在不同攻角和雷诺数下的气动特性，尤其是大攻角气动特性和前体涡与机翼涡耦合后空间涡流场结构演化的影响规律，为更好地进行先进高机动飞行器设计提供参考。

2 数值模拟方法

2.1 湍流模型

目前国际上各种复杂的分离流动模拟中常用的是DES(detached-eddy simulation)类方法。DES类方法的基本思路是用统一的湍流模型，以网格尺度和模型中的特征尺度隐式地划分大涡模拟(LES)和雷诺平均Navier Stokes(RANS)区域。DES 方法最初是基于SA(spalart allmaras)模型建立起来的，用LES方法模拟大尺度运动占主导地位的非定常分离湍流流动区域，用RANS方法模拟小尺度运动占主导地位的近壁区域。随着DES方法研究的深入，当边界层比较厚或者分离区较窄时发现了模型应力损耗(modeled stress depletion，MSD)问题。Menter和Kuntz最早在2004年基于SST(Shear Stress Transport)模型的混合RANS/LES方法中应用了消除MSD的方法，以避免网格精度不够高时，在边界层内DES转换为LES模式。2006年Spalart和Deck参照其思想发展了更通用的DDES方法。为了避免出现对数层不匹配问题，节省计算量，Shur和Spalart提出IDDES(improved delayed detached-eddy simulation)方法，其结合了DDES和壁面模型大涡模拟(wall-modeled large eddy simulation,WMLES)方法。针对翼身组合体飞行器大攻角流场的复杂性，本文计算中采用基于SA模型的IDDES类方法。

WMLES模型主要应用于非定常和有湍流的流动中，它通过长度尺度耦合RANS和LES，其湍流长度尺度定义为

=(1+)+(1-)

(1)

其中，为RANS模型湍流长度尺度，为LES模型湍流长度尺度。混合函数从0～1变化时，模型快速的从RANS模式(=1.0)过渡到LES模式(=0)。混合函数是用于修正由于RANS和LES交界面相互作用而损耗过多的雷诺应力。

IDDES采用了新的亚格子尺度的定义，它同时依靠网格大小和壁面距离，其湍流长度尺度定义为

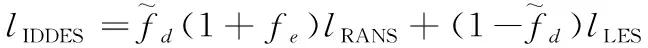
(2)

(3)

其中:为延迟函数，参数是模型长度尺度与壁面的距离的比值，为到壁面的距离，是涡粘性，, 是速度梯度，是冯卡门常数。

2.2 数值计算方法

由于迎风型NND格式形式简单，数值耗散较小，且计算量小，稳定性较好，本文数值模拟中对无粘项的空间离散都采用迎风型NND格式，非定常时间推进采用双时间步隐式迭代法。为了提高非定常的时间计算精度，同时又兼具较高的计算效率，时间推进采用Jameson提出的双时间步(dual-time-step)隐式迭代推进方法。

对于本文采用的IDDES混合湍流模型和非定常算法，已通过大量典型算例进行了考核和验证，典型算例包括细长圆锥有攻角绕流、Hummel单三角翼分离流动、低速圆柱绕流、跨声速方腔流动、超声速圆柱底部流动、NACA0012翼型俯仰振荡、NACA0015翼型深失速分离涡模拟等。图1、图2、图3给出了低速圆柱绕流的数值模拟结果。

图1 用密度着色的瞬时涡量等值面模拟图(Q=0.01)Fig.1 Isosurfacescoloured by the density of Q=0.01

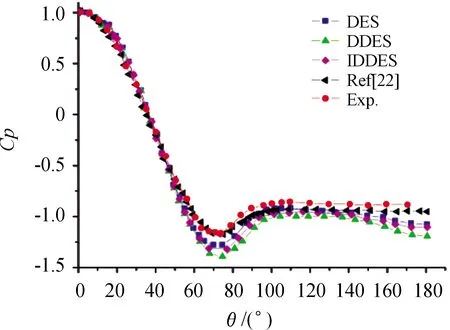
图2 壁面平均压力系数曲线Fig.2 Average wall pressure coefficient

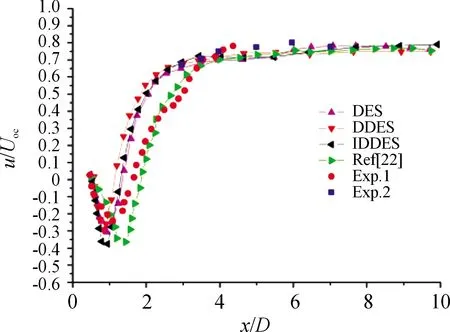
图3 流向速度在尾迹中心线分布曲线Fig.3 Velocity profiles along central streamline of wake region

图2是壁面压力系数与实验和Kravchenko计算结果的比较，实验数据来自Norberg，实验中雷诺数为4 020。

图3中的实验1数据来自Ong和Wallace，实验2的数据来自Lourenco 和Shih，可以看出，在1～4(是圆柱直径)区域，本文计算结果虽然与Ong和Wallace的实验结果差异较小，但在2～4区域与Lourenco 和Shih的实验结果基本一致。对比上述计算结果，可以看出本文采用的模型方法模拟精度较高。其他算例验证结果参见文献[25-26]。

2.3 网格和研究模型

脊形前体飞行器外形(翼身组合体WB1)取自Hall实验。其机头采用脊形角7.5°的脊形前体外形，全长=133.35 mm，后接脊形截面柱状机身；添加厚度1.27 mm的平板为机翼，嵌在脊形线上，机翼后掠55°，具体尺寸及几何外形如图4所示，单位为mm。图5给出了实验模型外形数据和本文根据数据点拟合的7.5°前体横截面模型数据曲线，其中是脊形前体截面高度，是宽度，单位均为mm。

图4 飞行器示意图Fig.4 Planform dimensions(mm)

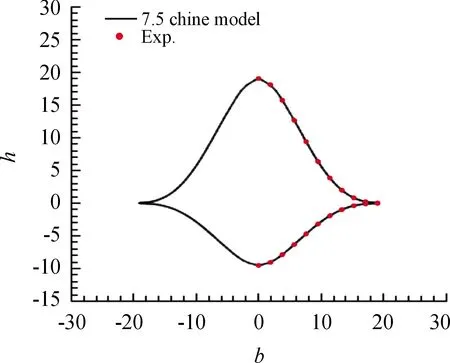
图5 7.5°脊形角计算模型横截面与水洞模型数据曲线Fig.5 Comparison of the cross-section of the 7.5°calculation model and the water tunnel model

文献[28-29]考察了网格疏密度对脊形前体计算结果的影响，为了后续计算中能给出较为准确的空间涡结构，满足IDDES模拟需求，且综合考虑计算效率，本文网格参照脊形前体模型G2的网格规模，采用C-H型多块对接网格，网格规模为2 455万，沿流向、法向和展向分布为373×201×181，其中机身上沿流线分布193个点，网格在壁面、机头、机翼前缘、尾缘及翼尖处加密，参见图6，物面法向第一层网格间距为1×10mm，确保<10。

图6 计算网格示意图Fig.6 Computation mesh

3 随雷诺数变化规律

飞机做战术机动和巡航时往往会在不同的海拔高度，因此本文研究了不同海拔高度时翼身组合体的气动特性，主要是雷诺数的影响，其中参考长度取为机翼根弦长，=190.5 mm时=1.77×10，1.1×10，0.65×10，分别对应海拔高度是0 km，5 km，10 km，取=04，=30°，= 0°，无量纲时间步长Δ=001，力矩积分关于重心轴向位置=222.9 mm。

图7为脊形前体飞行器模型不同雷诺数时气动力系数收敛曲线。从图7中可以看出，在所考察雷诺数下，气动力系数随雷诺数变化很小。

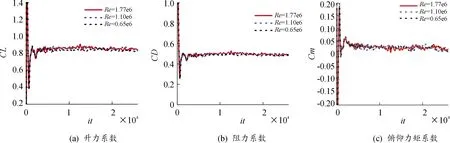
图7 气动力系数收敛曲线Fig.7 Convergence curves for aerodynamic coefficients

图8为用压力着色的等值面云图，取=0001，=(-)(+)，和分别为旋转张量和应变率张量。本文选取Q涡准则是由于Q涡准则消除了边界层中平均切应力和靠近分离的早期剪切层的影响，比涡度准则更能反映主要的涡结构。

从图8可以看出，所考察的3个雷诺数下前体涡和前缘涡破裂点和强度差别不大，可见在所考察雷诺数范围内雷诺数变化时流场结构趋同，对称性较好。文献[9]中Hall研究了低雷诺数(=14×10)的水洞数据和高雷诺数(=06×10)风洞试验数据之间的比较，研究对象为圆形机身，尽管由于机身改变了主翼的有效攻角、水洞和风洞模型缩比尺寸不同以及雷诺数的差异，使水洞和风洞试验得出的涡破裂攻角不同，但涡结构类似，变化趋势相同，所以，水洞实验数据有较高的可参考性。同时， Hall也指出，雷诺数在一定范围内变化时，脊形前体由于脊形边的存在，前体涡更强，风洞与水洞涡结构类似。

图8 不同雷诺数时用压力着色的Q等值面云图(Q=0.001)Fig.8 Isosurfacescoloured by the pressure of Q=0.001 at different Reynolds number

4 随攻角变化规律

攻角是很重要的来流参数，为了分析攻角的影响规律，主要研究了攻角从5°～60°变化时对翼身组合体升阻特性、横航向特性的影响。取来流马赫数= 04，攻角分别为= 5°～60°，=0°，无量纲时间步长Δ=0.01，海拔0 km的大气参数，=288.16。基于上述雷诺数研究，本节计算数据与Hall实验数据作简单的对比，重点分析前体涡和机翼前缘涡随攻角演化规律。

图9(a)、图9(c)中给出了攻角15°和30°时用马赫数着色的空间流线，图9(b)和图9(d)为攻角15°和30°时Hall的水洞实验结果，与计算结果对比可以看出，前体涡和前缘主涡位置和破裂点相似，表明本文计算方法具有较高的精度。

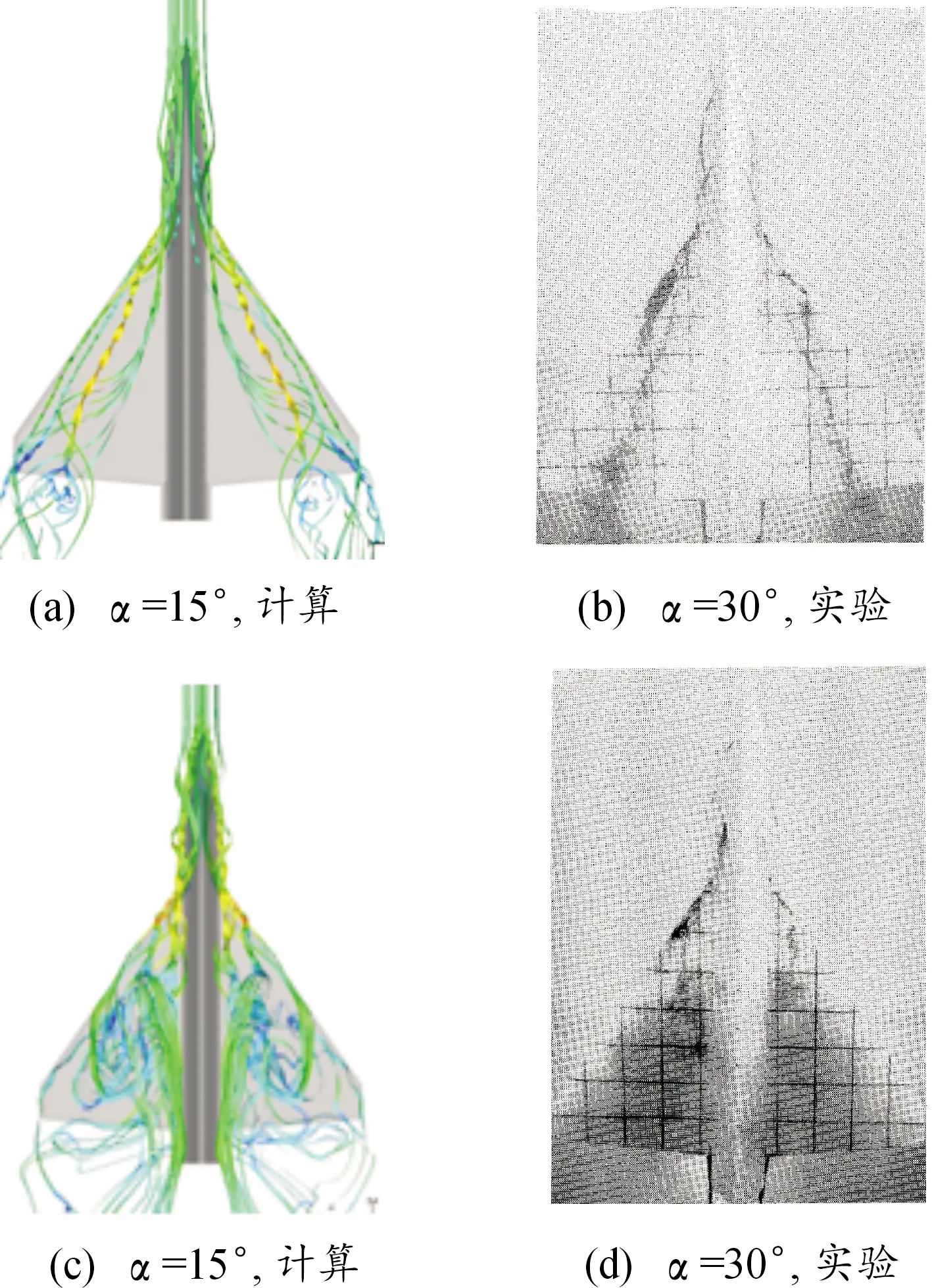
图9 空间涡结构示意图Fig.9 Space vortex structure

图10为用压力着色的等值面云图，取=0001。从图10中可以看出,在5°攻角已经出现前体涡和前缘涡，15°攻角时前缘涡从机翼尾部开始破裂，破裂点随攻角增加逐渐向机翼前缘靠近。图11为不同攻角下用马赫数着色的空间流线云图。可以看出：10°攻角时，前体主涡和前缘主涡没有耦合，在机翼上产生二次涡，前缘主涡在机翼尾部破裂。15°攻角时，前体涡和前缘涡进一步增强，前缘涡向机身内侧靠拢，与前体涡耦合。20°攻角时，单独前体主涡下面有明显二次涡(图12)，单独前体数值模拟数据参见文献[27-28]，而翼身组合体模型前体没有出现明显二次涡，前体主涡在机翼中部也与前缘涡耦合，前缘涡破裂点比15°攻角时大幅靠近机身顶点。随着攻角继续增大，30°攻角时，前体涡和前体二次涡向机身内侧移动，前体涡和前缘涡进一步抬升，前体主涡、前缘二次涡和前缘主涡耦合，使得前缘主涡进一步增强；单独脊形前体在二次涡外侧形成三次涡，而翼身组合体没有前体三次涡。40°攻角时，前体涡破裂点向机头方向移动，前体二次涡外侧形成三次涡，并与前缘涡耦合。50°攻角时，前体主涡破裂点继续前移，与前缘涡解耦，该攻角时通常认为主翼已经严重失速，但由于脊形前体二次涡和三次涡与前缘涡耦合，延迟了主翼前缘涡的完全破裂；与单独脊形前体相比，前体涡破裂点大幅后移。60°攻角时，前缘涡完全破裂。

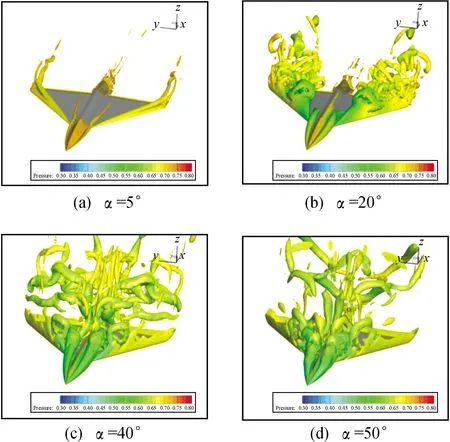
图10 不同攻角时用压力着色的Q等值云图(Q=0.001)Fig.10 Isosurfacescoloured by the pressure of Q=0.001 at different angle of attack

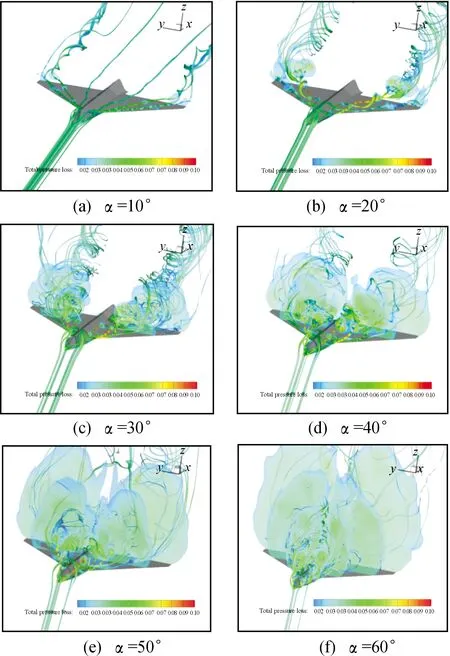
图11 WB1模型空间流线和截面总压损失云图Fig.11 Streamline and total pressure loss at the section of WB1 model

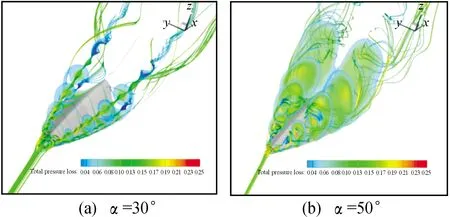
图12 前体模型空间流线和截面总压损失云图Fig.12 streamlines and total pressure loss at the section of chine forebody model

图13为轴向位置背风面的表面压力分布曲线，可见，在所研究攻角范围内，机翼和前体背风面压力具有较好的对称性；由于前体涡和前缘涡的影响，在飞行器背风面存在明显的低压区，随着攻角增大，前体涡和前缘涡向下拉，表面压力极值变大，但随着攻角继续增大，前缘涡和前体涡破裂，表面压力极值变小。

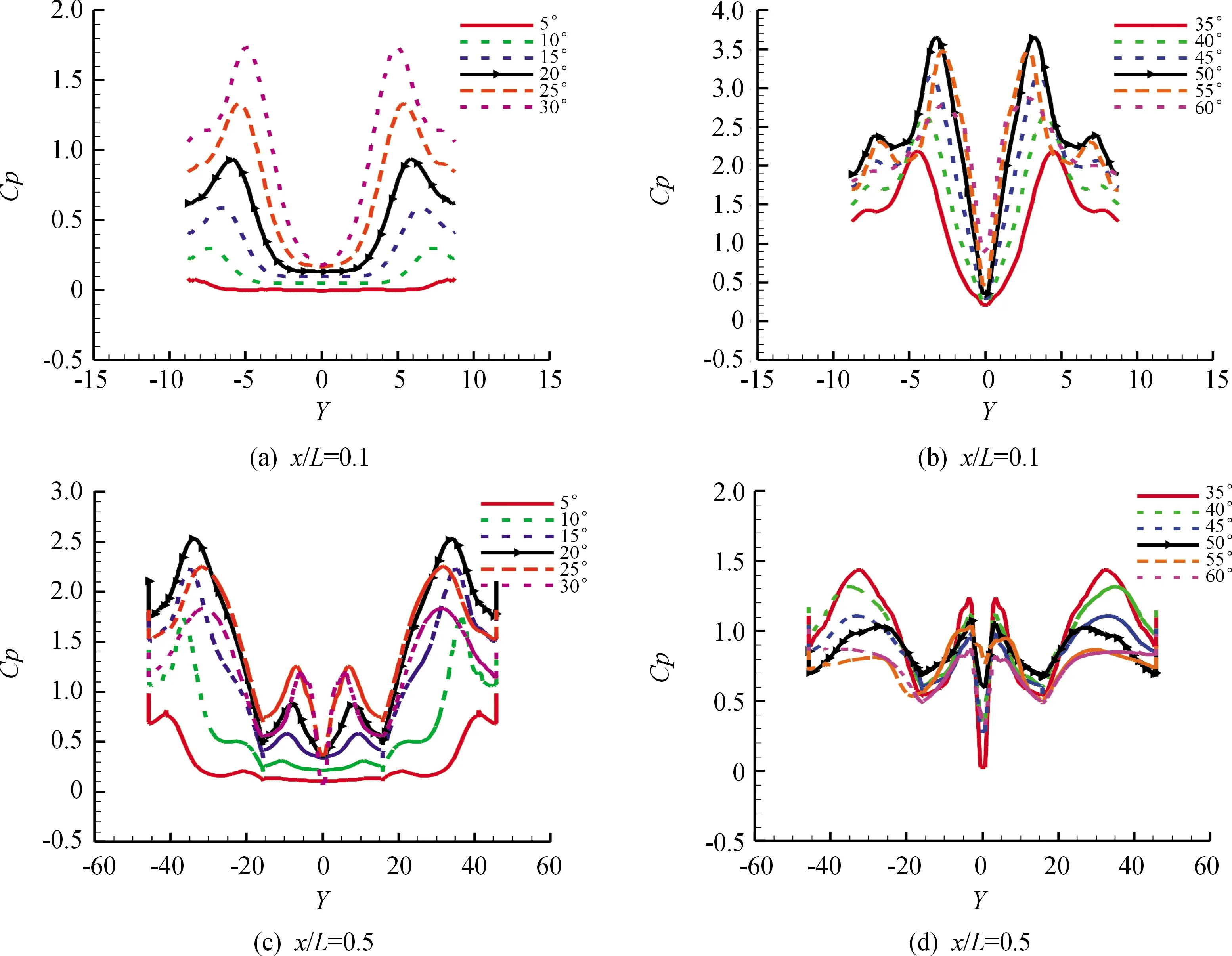
图13 背风面截面压力系数分布曲线Fig.13 Pressure distributions at constant axial locations of leeward side

图14为=04时气动力系数随攻角的变化曲线，气动力系数值是每50步输出计算结果然后求时间平均。从图14可以看出：<15°时，升力系数随攻角线性增加；15°<<25°时，增加变缓，但仍呈线性增加；25°<<40°之间变化缓慢；>40°时，开始减小。阻力系数随攻角增加而增加。随攻角增加，侧向力系数、滚转力矩系数和偏航力矩系数都趋于零。

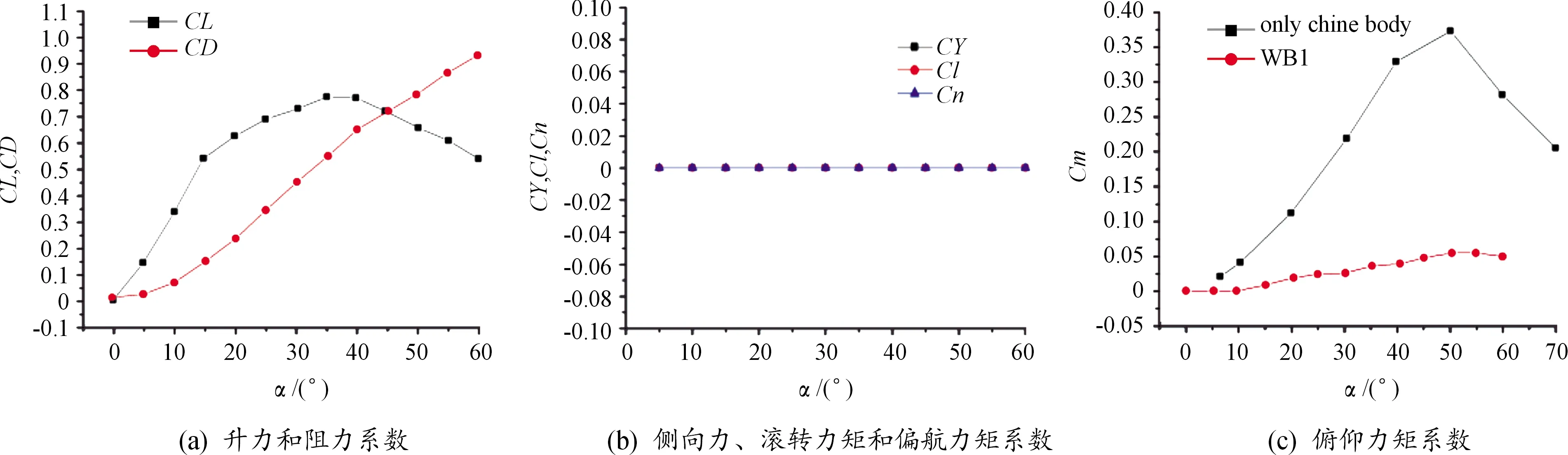
图14 气动力系数随攻角变化曲线Fig.14 Aerodynamic coefficients variation with the angle of attack

可见，机翼前缘涡对脊形前体主涡有明显的卷吸作用，极大地延缓了前体主涡的破裂，这导致机翼前缘涡破裂后，前体涡诱导的升力仍随攻角增加而增大，整体失速特性有明显改善。机翼前缘涡诱导脊形前体主涡更靠近壁面，因而抑制了前体二次涡、三次涡产生和发展，相应地，也延缓了前体二次涡、三次涡的破裂攻角；前体二次涡、三次涡与机翼前缘涡先后耦合，延迟了机翼前缘涡的完全破裂，这导致在25°<α<40°之间整体升力变化缓慢，也改善了失速特性，且较单独脊形前体，流场对称性保持更好。由于机翼前缘涡诱导低头力矩，与脊形前体涡诱导抬头力矩相互抵消，导致翼身组合体的纵向稳定性特性，较单独脊形前体有明显改善。

5 结论

所研究雷诺数对脊形前体飞行器气动力系数和涡流场结构影响较小。攻角变化时，机翼前缘涡对脊形前体主涡有明显的卷吸作用，极大地延缓了前体主涡的破裂，并诱导脊形前体主涡更靠近壁面，因而抑制了前体二次涡、三次涡产生和发展，相应地，也延缓了前体二次涡、三次涡的破裂攻角；前体二次涡、三次涡与机翼前缘涡先后耦合，延迟了机翼前缘涡的完全破裂，整体失速特性有明显改善。且较单独脊形前体，无侧滑时流场对称性保持更好。由于机翼前缘涡诱导低头力矩，与脊形前体涡诱导抬头力矩相互抵消，导致翼身组合体的纵向稳定性特性，较单独脊形前体有明显改善。

高机动飞行器一般不以大攻角平飞，而是机动进入或经过大攻角状态。静态大攻角绕流是一种近似模拟，后续将进一步研究高机动飞行器的动态气动特性。