一个非对称不等式问题的探究

湖南省桃江县第一中学 (413400) 胡芳举

湖南省岳阳县第一中学 (414100) 胡燕玲

题目已知a,b,c≥0,a+3b+5c=9，求证：3a+3ab+4abc≤36.

本题是安振平老师在叶军数学工作站第177期问题研究栏目提供的一个不等式：本文将给出该不等式的两种证法以及三个变式.

证法一：记M=3a+3ab+4abc.

2.当b>1时，设b=1+d(d>0)，则a=6-3d-5c,M=36-(12cd2+20dc2+20c2+3cd+9d2+6c)<36.

综上，M≤36(当a=6,b=1时取等号).

变式1 已知a,b,c≥0,a+3b+5c=9，m≥5，求3a+3ab+mabc的最大值.

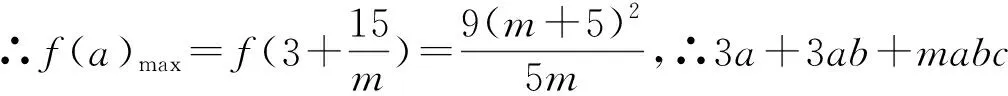
变式2 已知a,b,c≥0,a+3b+5c=9，求使不等式3a+3ab+mabc≤36恒成立的最佳常数m.