“一题一课”从确定教学主题开始
——由一堂教学公开课引发的思考
江苏省溧水高级中学 (211200) 孙 莹
“一题一课”首先是通过对典型例题的深入研究,在明确问题本质的基础上,通过纵横联系,提炼问题的思想方法,通过迁移拓展,形成解题套路;然后,在立足学情的基础上,科学、合理、有序地组织学生进行相关的数学探索活动,从而完成一节课的教学任务,以此达成多维目标的过程.“一题一课”为学生提供了自主思考平台,有助于理清知识脉络,具有加深对知识的理解,培育创造性思维,发展核心素养等教学价值.虽然,“一题一课”的“题”是“课”的载体,在教学中处于核心地位,但这只是一方面,当“题”确定好后,教学主题的选择其实更为重要,因为它直接决定教学的目标与教学的成效.最近,笔者观摩了一堂教学公开课,对此深有感触.
1 教学过程简介

作为高考填空题的压轴题,此题以“投影”概念为认知的起点,考查学生的平面向量运算能力与综合运用知识的能力.入口宽,方法多,视角广,立意高是此题的一大特点,这些特点完全符合“一题一课”的选题标准.
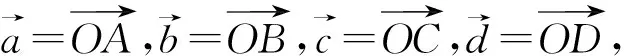

图1
学生发现|OD|2+|DE|2不易得,于是有学生提出从坐标入手进行计算.


接下去,进入小组合作环节.经过学生讨论,得出了以下两种求解方案.
最后,教师又补充了一种方法.
虽然得到了以上三种解法,问题看似解决了,但纵观整堂课还是显得比较凌乱,主要表现为:一是,一开始教师打算从形入手,但由于碰到了障碍,受学生的影响转而从数入手,从“形”入手到底是否行得通,最后还是悬而未决?二是,通过类比获得了点到面的距离公式,但这个公式多数学生事先并没有接触过,教师也没给出证明,那么数学的严密性是否受到影响?三是,也是最为致命的,“一题一课”的教学目标是什么,是为了获得正确的解法,还是为了“做一题、得一法、通一片”? 因此,当最后教师问学生“这节课学会了什么”时,多数学生的回答是“记住了点到面的距离公式”,而这节课所呈现出来的核心思想方法却被学生“忽略”了.
2 教学主题是“一题一课”的起始点
“一题一课”最大的优势就是围绕着教学目标,通过“题”的深度挖掘,以“原题”为出发点, 立足学生的认知规律,进行不同层次的探究题,通过深入浅出的剖析,提炼数学思想方法,获得解题套路,从而提升学生的解题水平.但“题”确定好后,教学主题并没有同时得到确定,因为,一道“题”按照不同的方向可以衍生不同的教学主题,如果在教学主题没有得到明确的前提下,而是随题发挥,就很容易导致就题论题或者教学逻辑混乱.正如本节课一样,由于教学主题事先没有得到明确,从而使得教学过程变成了“解题方法的罗列”,变成了对“公式的记忆”.
2.1 立足学生学情,确定一个主题
在对教学主题的确定中,教师首先应该根据学生的学习特点、知识掌握程度等梳理学生存在的方法短板与思维漏洞,寻找教学的切入口.遵循学生的成长特征, 从认知、习惯与数学水平着手,精心选择典型的例题,将巧妙的教学方法融入到“一题一课” 的课堂中.也就是说,通常情况下,“一题一课”是先确定主题,然后再选择例题.当然,也可以先有例题,但教师首先要对例题进行细致的剖析,明确其教学功能与价值,然后,在选择一个视角确定教学主题.
2.2 立足问题设计,夯实一种方法
皮亚杰认为“学习过程并不是个体获得越来越多外部信息的过程,而是能动地建构新的认知图式,不断完整新的认知结构的过程”.“一题一课”旨在通过少量题目的训练,而达到理想的教学目标,因此,在例题选择好后,围绕着例题精心设计问题,通过问题驱动,引导学生从变中发现不变的本质, 从不变的本质中发现变的规律,从而在实现知识的系统化与网络化的同时获得“解决一类问题的方法”.
3 本节课的教学改进
基于上述分析,那么本节课的教学主题如何确定,教学过程如何设计?本题是以“向量”为背景,但最后要求的却是一个三元最值问题,因此,本节课至少有两个教学主题可供选择,一是向量问题的解题策略,二是多元最值问题的解题策略.
3.1 教学主题一:多元最值问题的解题策略
如果以多元最值为教学主题,那本节课的教学重点就应该放在如何求三元最值上,教师需对解题策略按照由易到难进行逐步呈现.
对于三元最值问题,学生还是有经验的,因为在求二元最值问题时,很多时候是通过“消元”解决的,这种解题思路同样可以推广的三元.

这样设计的好处在于所有的解题方法都与学生熟悉的二元最值问题联系起来,从而有助于学生解题思想的形成,这远比补充一个没有经过严格证明的点到面的距离公式更容易让学生接受与理解.
3.2 教学主题二:向量问题的解题策略
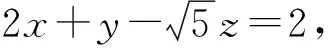
在数学“一题一课”中,题与教学主题根本是两回事,切不可以题来代替教学主题,使得解题教学被题所绑架.无论是先确定主题,再甄选例题,还是直接从题中确定主题,教学主题都应该放在第一位,“一题一课”就要从确定教学主题开始.

