基于改进差分进化算法的三相逆变系统分数阶PI控制策略

方锦辰，王 环，胡 文

(温州大学 电气数字化设计技术国家地方联合工程实验室，浙江 温州 325035)

0 引言

随着环境污染和能源危机问题的日益加剧，新能源发电和电动汽车迎来了广阔的发展前景，包括光伏发电技术、风力发电技术、异步电机驱动技术都得到了大力发展[1-2]。三相逆变系统在上述技术中起着至关重要作用，其逆变性能直接决定了输出电能质量的优劣，进而影响整个系统的稳定运行[3]。在应用过程中发现，三相逆变系统常常存在输出电能谐波畸变率高、抗干扰性能差等问题，如何提高三相逆变系统输出性能成为众多学者研究的热点。用于三相逆变系统的传统控制策略包括比例-积分-微分(PID，proportional integral derivative)控制、比例谐振控制、无差拍控制、重复控制和预测控制等，这些策略都已较为成熟，后期通过学者不断改进，在一定程度上改善了三相逆变系统输出的电能质量[4-6]。由于双闭环PI控制策略结构简单，硬件实现方便，适应性强，在三相逆变系统中具有较大的应用前景[7-8]。但是，三相逆变系统双闭环PI控制器的参数整定往往依赖于设计人员和工程师的经验，通常难以快速地获得一组最优整定参数，在实际工程应用中难以获得最优控制性能。

分数阶PID(FOPID，fractional-order PID)控制器相对于整数阶PID控制器增加了积分阶次和微分阶次两个控制参数，设计更加灵活多样，使得FOPID控制器具有更好的控制精度和鲁棒性[9-10]。近年来，分数阶PID控制及其改进方法在复杂工业系统、新能源微电网系统、多区域互联电力系统等领域中都得以成功应用[11-14]。文献[11]针对分数阶控制系统，提出了一种基于二进制编码极值优化的分数阶PID控制器优化设计方法(简称BCEO-FOPID)，通过大量的仿真实验证明了分数阶PID控制器不管在分数阶控制系统模型还是整数阶控制系统模型都较整数阶PID控制器具有明显的优势。更进一步地，文献[12]将BCEO-FOPID方法推广应用到了独立微电网频率控制中，从而验证了分数阶频率PID控制器相比基于二进制遗传算法的FOPID/PID控制器、基于二进制粒子群优化的模糊FOPID控制器的优势。文献[13]针对自动电压调节系统，综合考虑了系统误差绝对值的累加和、稳态误差、调节时间等多种控制性能指标，提出了一种基于多目标极值优化的分数阶PID控制器优化方法(简称MOEO-FOPID)，获得了较好的Pareto前沿；并通过与基于遗传算法、粒子群优化算法、混沌蚁群算法、改进的非支配排序遗传算法(NSGA-II)的FOPID与PID控制器的对比实验，从而验证了MOEO-FOPID的优势。文献[14]针对多区域互联电力系统负荷频率控制问题，设计了一种基于自适应种群极值优化算法的分布式分数阶PID控制策略(简称APEO-FOPID)，仿真实验表明：APEO-FOPID相比基于遗传算法、粒子群优化算法和NSGA-II的FOPID控制器具有更好的控制性能。但是，分数阶控制理论在电力电子变换器中的应用还处于起步阶段。文献[15]针对升压型直流-直流变换器，采用高性能数字信号处理器对分数阶PID控制器进行了硬件实现，通过实验验证了：在负载突变和输入电压变化的情形下，分数阶PID控制器相比传统整数阶PID控制器具有更小的超调量和更短的调节时间。文献[16]则针对降压型直流-直流变换器，验证了分数阶PID控制器相比传统整数阶PID控制器具有更佳的控制性能。但上述研究存在两方面的不足：1)分数阶控制理论在三相逆变系统中鲜有应用；2)分数阶PID控制器的参数依赖于设计人员的经验，并未采用智能优化算法对分数阶PID控制器的参数整定进行研究。

随着微电网、电力电子变换系统和大电网系统日益复杂化以及各种不确定因素的增多，控制器参数整定已变得越来越困难。智能优化算法的优势逐渐突显出来，可以解决较多的非线性、不可微和多极值的复杂优化问题[17]，且后期不断有学者对算法进行改进，在函数优化和参数寻优等方面取得显著效果[18-19]，将有助于研究人员和工程师解决复杂工业系统控制器优化设计难题。差分进化(DE，differential evolution)[20-21]是一种基于种群的启发式随机搜索算法，具有原理简单、受控参数少、鲁棒性强等特点，在解决非线性优化问题上表现突出，在生产调度、电网规划、负荷经济分配、系统优化设计等领域都得到了广泛的应用，但在三相逆变系统和微电网系统的分数阶控制器优化设计中应用还十分有限。此外，标准差分进化算法也存在易早熟收敛和对算法参数敏感的问题，文献[22]有效地利用了前期个体进化产生优质解的经验，通过记录成功试验个体的交叉概率CR和缩放因子F的大小，求其平均值，并将其代入到后续迭代进化中去，有效解决了差分进化算法参数难以精准选取的问题。文献[23]采用粒子群算法和差分进化算法构成的混合优化算法，极大地改善了差分进化算法易早熟收敛的问题。通过改进差分进化算法避开其不利的影响，充分发挥优势，对于工程推广应用具有重要意义。

基于上述讨论，本文提出了一种基于改进差分进化算法(IDE，improved differential evolution algorithm)的三相离网型逆变系统分数阶PI控制策略(简称IDE-FOPI)。首先采用Oustaloup近似化处理方法构造分数阶PI控制器，分析分数阶控制器相比传统整数阶控制器所具有的优势；然后，基于机理分析法和dq坐标变换方法建立三相离网型逆变系统的数学模型，根据数学推导在MATLAB/Simulink中搭建其双闭环分数阶PI控制的仿真模型；分别利用遗传算法(GA，genetic algorithm)、粒子群算法(PSO，particle swarm optimization)、标准差分进化算法(DE)和IDE对分数阶PI控制器和整数阶PI控制器参数进行优化整定，比较几种优化算法在逆变控制器中的优化效果，从而验证IDE-FOPI的有效性。

1 基于分数阶PI控制的三相离网逆变系统

1.1 分数阶PI控制器

分数阶微积分是传统微积分的广义形式，目前已经越来越多地被应用在复杂控制系统建模和控制器的设计上，极大地提高了建模的精度以及综合控制性能。分数阶PID控制器参数在原整数阶PID控制器基础上增加了参数λ和μ，极大地扩展了控制器的调整范围，在提升总体性能方面起到了很好的积极作用[24-25]。

本文采用分数阶微积分的Oustaloup近似处理方法[26]来构造分数阶PI控制器。选择拟合频率段为(ωb，ωh)，设置近似阶次为N，构造连续滤波器的传递函数模型为：

(1)

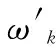
(2)

(3)

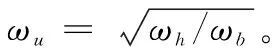
分数阶PIλ控制策略是按照控制器输入输出的比例、积分的线性组合来调节控制量，其传递函数的表达式为：

(4)

Kp表示比例系数，Ki表示积分系数，λ表示分数阶积分的阶次。分数阶PIλ控制器对应的频域特性为：

(5)

对数频率特性为：

L(ω)=20×

(6)

(7)

其中：积分项sλ在对数幅频特性曲线中，它的斜率是-20λdB/dec，相位裕度为(πλ/2)。文献[26]描述了分数阶微积分阶次λ对系统性能的影响，即改变积分阶次λ可以调节控制系统频率特性中的低频部分，选择适当的λ可以减小系统稳态误差并同时提高系统的动态特性。分数阶PIλ控制器对应的伯德图(Kp=1，Ki=1，λ分别取不同阶次)如图1所示。

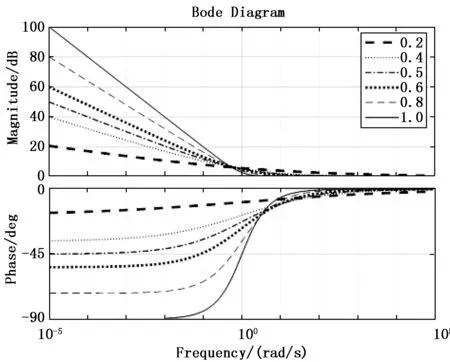
图1 分数阶PIλ控制器在不同积分阶次时的伯德图

由图1可以看出：分数阶PIλ控制器对应幅频特性曲线的斜率随着分数阶积分阶次λ的降低而减小；相频特性曲线随着积分阶次λ的降低，对应的稳定裕度将变大。因此，分数阶PIλ控制器在稳定性和快速性等方面相比整数阶PI控制器均有所提高。

1.2 三相离网逆变系统模型搭建

本文以三相离网型逆变系统为研究对象，采用LC滤波电路作为滤波模块，并采用电压外环与电流内环的双闭环分数阶PIλ控制策略。利用基尔霍夫电流定律KCL、基尔霍夫电压定律KVL等机理分析方法，建立LC逆变电路模型：

(8)

式中，uo为输出电压；u为逆变器侧输出电压；iL为电感电流。

本文采用空间矢量脉宽调制(SVPWM，space vector pulse width modulation)方法，将三相电压和电流转换到同步旋转坐标系下，公式(9)～(10)为三相电流坐标变换公式：

(9)

(10)

在坐标变换过程中会产生耦合分量，具体过程如下：

(11)

(12)

式中，C3s/2r为三相静止坐标系到两相旋转坐标系的变换公式；id和iq分别表示dq坐标系下的d轴电流和q轴电流；iabc为三相静止坐标系下的三相电流。

当三相平衡时，根据公式(9)～(12)可以得出LC滤波电路两相旋转坐标系下的电流模型：

(13)

式中，iLd和iLq分别表示电感电流在d轴和q轴上的分量；uod和uoq分别表示输出电压在d轴和q轴上的分量；ud和uq分别表示逆变器侧输出电压在d轴和q轴上的分量；r为滤波电路等效电阻；Lf为滤波电感。

同理可得LC型滤波电路的电压模型：

(14)

式中，iod和ioq分别表示输出电流在d轴和q轴上的分量；Cf为滤波电感。

由公式(12)可知：电压电流在dq轴之间存在耦合分量，任何一轴的电压电流扰动都会传递到另一轴，进而影响三相逆变系统的控制性能。采用分数阶PI双闭环控制策略，同时考虑解耦控制，双闭环控制系统表达式如下所示：

(15)

式中，Vdref和Vqref分别表示参考电压在d轴和q轴的分量；idref和iqref分别表示电感电流参考值在d轴和q轴的分量。

(16)

式中，udref和uqref为控制环送入到SVPWM调制模块的d轴和q轴参考电压。

结合上述公式和三相逆变系统的运行原理搭建相应的三相逆变系统双闭环分数阶PI控制模型，如图2所示。逆变器模块通过LC滤波电路给负载电阻供电，三相分数阶逆变控制系统包括电压外环分数阶控制回路和电流内环分数阶控制回路；在两相旋转坐标系下，计算参考电压Vdref、Vqref和实际电压差值，送到电压外环分数阶PI模块经计算得到dq轴电感电流参考分量idref和iqref，考虑耦合分量的影响通过加减将其消除，将参考电流和实际电感电流的差值送入电流内环分数阶PI模块计算得到udref和uqref，消除耦合分量送入到SVPWM模块控制IGBT开关器件导通与开断。需要重点强调的是，分数阶PI模块控制参数的整定效果对三相逆变系统输出电压的稳态特性和动态特性起决定性作用。

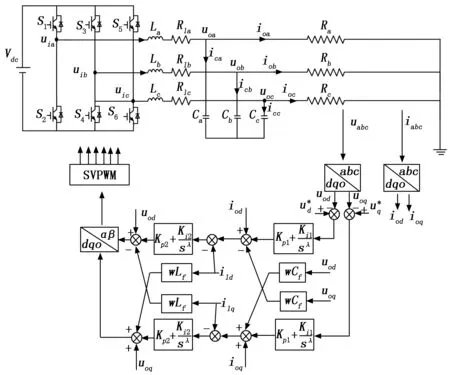
图2 三相逆变系统双闭环分数阶PI控制模型结构图

2 改进差分进化算法在三相逆变系统双闭环分数阶PI控制器中的应用

为了改善DE算法易出现“早熟”的问题，本文提出了一种基于自适应多变异操作策略和参数自调节的改进DE算法(IDE)，并将其应用于三相离网逆变系统分数阶PI控制器优化设计中。

2.1 标准差分进化算法

针对最小化优化问题minf(x1，x2，...，xD)，标准差分进化算法主要包括变异、交叉和选择3个基本操作算子，其主要步骤如下：

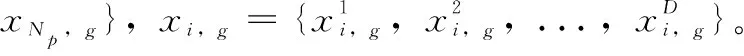
初始个体随机生成，如式(17)所示：

(17)

步骤2：变异操作。通过差分策略实现个体变异，DE/rand/1变异策略表示为：

vi，g=xr1，g+F*(xr2，g-xr3，g)

(18)

式中，r1，r2和r3为种群中3个不同的个体；F为缩放因子，F越大，越有利于全局寻优，反之则适于局部寻优。

步骤3：交叉操作。通过将目标个体向量和变异向量进行交叉混合构造新的个体，具体过程如下所示：

(19)

式中，randnj表示产生一个一个小于D的随机整数；目的是保证在交叉操作中至少有一个元素进行交换；从而保证交叉操作中个体的进化；CR为交叉概率。

步骤4：选择操作。

(20)

式中，xi，g为当前个体。采用“贪婪”策略进行选择操作，将试验个体与目标个体的适应度值进行比较，如果试验个体的适应度值较优，将试验个体作为子代，反之则保留目标个体。

2.2 改进差分进化算法

本文在上述标准差分进化算法的框架基础上，提出了一种改进的差分进化算法，主要改进体现在两方面：1)提出了一种改进的自适应多变异操作策略；2)设计了缩放因子F和交叉概率CR等算法关键参数自调节策略。

1)自适应多变异操作策略。标准差分进化算法采用单一的变异策略，往往难以实现全局搜索和局部搜索的平衡。本文根据个体适应度值和迭代情况对3种变异策略进行自适应选择。所述的3种变异策略具体如下所示：

变异策略1：DE/current-to-best/1

vi，g=xi，g+F·(xbest，g-xi，g)+F·(xr1，g-xr2，g)

(21)

变异策略2：DE/current-to-pbest/1

vi，g=xi，g+F·(xpbest，g-xi，g)+F·(xr1，g-xr2，g)

(22)

变异策略3：DE/rand/1

vi，g=xr1，g+F·(xr2，g-xr3，g)

(23)

式中，xpbest为个体适应度值排在前20%的个体。

首先，设计了一种随着迭代次数变化的概率函数Pc，如式(24)所示；根据概率函数对变异策略3和变异策略2进行选择，如式(25)所示：

(24)

(25)

式中，Pc为随迭代次数变化的概率函数，Pc，min和Pc，max分别表示Pc的下限和上限。在迭代进化初期，Pc函数值较小，能够较大概率执行变异策略3，反之则更容易执行变异策略2，保证种群迭代初期全局寻优能力和迭代后期局部寻优能力。

其次，按照适应度值大小将种群划分成两部分，适应度值排在前20%的个体采用变异策略1，增强局部搜索能力；剩余适应度值一般的个体，则根据式(22)和(23)执行变异策略。在变异策略2中，采用xpbest代替传统的xbest，xpbest从适应度值前20%的个体中随机获取，这种方式平衡了局部搜索和全局搜索能力，既避免算法陷入局部最优同时又加快了收敛速度。为了避免搜索陷入停滞，进一步提高搜索性能，当种群最优适应度值经过T代后还没有更新，则将原先执行变异策略1的个体改为执行变异策略2，从而改变较优群体的搜索方向。

2)算法关键参数自调节策略。缩放因子F和交叉概率CR作为差分进化算法变异操作和交叉操作的关键参数，对优化性能有着重要影响。如果这些算法关键参数在优化过程中采取固定的数值，很容易导致差分进化算法陷入局部最优，且不利于优化算法收敛。为此，对这些关键参数的选取进行改进，将有助于提升差分进化算法的寻优性能。考虑到个体适应度值差异和迭代次数的影响，在适应度值较优的个体附近更容易产生适应度值优良的个体，此时应适当减小缩放因子。交叉概率应随着迭代次数的增加而增大，前期较小的交叉概率可以保证种群的多样性，后期较大的交叉概率则保证算法的局部寻优能力。因此，将缩放因子F和交叉概率CR进行如下自调节，如式(26)和(27)所示：

(26)

(27)

式中，N表示正态分布，使缩放因子和交叉概率在一定范围波动；n表示种群中个体适应度按照升幂排列的排序值，FLmin和FUmin分别表示缩放因子最小值的下限和上限，FLmax和FUmax分别表示缩放因子最大值的下限和上限，CRmin和CRmax分别表示交叉概率的下限和上限。

2.3 基于改进差分进化算法的三相逆变系统分数阶PI控制器优化过程描述

描述三相逆变电源输出的电能质量主要包括两个指标，电压畸变率和电压误差。本文将主要通过时间乘误差绝对值积分(ITAE，integral of time weighted absolute error)和总谐波失真(THD， total harmonic distortion)两个指标加权叠加构成优化目标函数。优化目标函数值越小，表示电压畸变率和ITAE误差值越小。

优化目标函数和约束条件表达式具体如下：

x=(Kp1，Ki1，Kp2，Ki2，λ)

s.t.l1≤Kp1≤u1

l2≤Ki1≤u2

l3≤Kp2≤u3

l4≤Ki2≤u4

l5≤λ≤u5

(28)

式中，x为决策变量，w1，w2分别为电压ITAE和THD的权重系数；l1，l2，l3，l4分别为Kp1，Ki1，Kp2和Ki1的下限；u1，u2，u3和u4分别为Kp1，Ki1，Kp2和Ki1的上限。

基于改进差分进化算法的三相逆变系统分数阶PI控制器优化的主要思路是通过改进差分进化算法的演化过程来迭代求解如式(28)的优化问题，具体的优化流程如图3所示。详细的算法步骤如下：

图3 基于改进差分进化算法的三相逆变系统双闭环分数阶PI控制器优化流程图

步骤1：按照1.2小节所述方法，通过机理分析法和坐标变换法，搭建如图2所示的三相逆变系统dq坐标系下双闭环分数阶控制模型。

步骤2：初始化IDE算法参数设置，包括种群数目Np，最大进化代数G，缩放因子最小值的下限和上限(FLmin和FUmin)，缩放因子最大值的下限和上限(FLmax和FUmax)，交叉概率的下限和上限(CRmin和CRmax)，变异策略选择概率函数Pc的下限和上限(Pc，min和Pc，max)。

步骤3：随机生成一个种群规模为Np且满足式(28)约束条件的实数编码初始化种群X，种群中每一个个体表示三相逆变系统双闭环分数阶PI控制器的参数(Kp1，Ki1，Kp2，Ki2，λ)。

步骤4：将种群中的每一个个体对应的分数阶控制器参数传输到三相逆变系统仿真模型中，运行仿真模型，并按照式(28)中的目标函数计算每个个体的适应度值，并将种群中当前最小的适应度值设置为fbest，将对应的个体设置为当前最好解xbest。

步骤5：按照式(26)和(27)对缩放因子F进行计算，并按照2.2小节(1)中所述的自适应多变异操作策略执行变异操作。

步骤6：按照式(26)对交叉概率CR进行计算，并按照式(19)执行交叉操作。

步骤7：按照式(20)执行选择操作。

步骤8：重复步骤(4)～(7)直到迭代次数达到最大进化代数G。

步骤9：输出最佳的适应度值fbest和对应的最佳个体xbest(即最佳的双闭环分数阶PI控制器参数)。

3 三相逆变系统优化控制策略的仿真验证

3.1 三相逆变系统性能测试

为了验证本文提出IDE-FOPI优化控制策略的可行性和优势，搭建如图2所示的三相逆变系统仿真模型。在此，表1给出了仿真实验中的三相逆变系统参数值，包括直流电源电压、滤波电感、滤波电路等效电阻、负载电阻和额定频率。

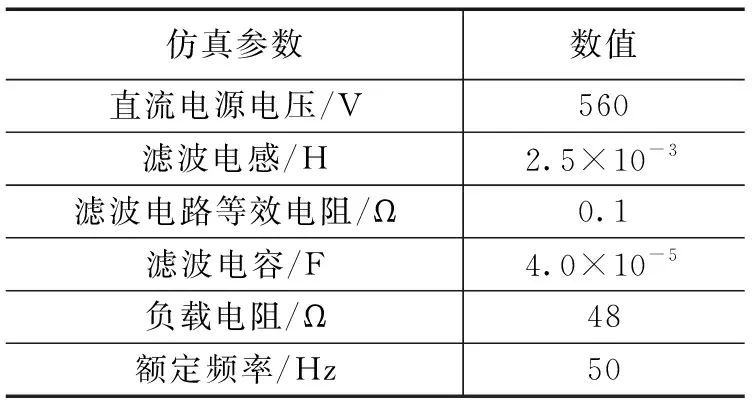
表1 三相逆变系统模型的仿真参数

采用GA、PSO、DE和IDE算法分别优化三相逆变系统整数阶PI控制器参数，将对应的算法分别标记为GA-PI、PSO-PI、DE-PI、IDE-PI；同时，采用GA、PSO、DE和IDE算法分别优化三相逆变系统双闭环分数阶控制下的FOPI参数，将对应的算法分别标记为GA-FOPI、PSO-FOPI、DE-FOPI、IDE-FOPI。表2给出了GA、PSO、DE和IDE优化算法的具体参数设置。

表2 GA、PSO、DE和IDE的算法参数初始化设置

图4(a)给出了IDE-FOPI与整数阶PI控制算法 (GA-PI、PSO-PI、DE-PI、IDE-PI)的优化迭代过程曲线比较；图4(b) 给出了IDE-FOPI与其它分数阶PI控制算法(GA-FOPI、PSO-FOPI、DE-FOPI)的优化迭代收敛过程的比较。从图4(a)可以看出，本文提出的IDE-FOPI相比GA-PI、PSO-PI、DE-PI、IDE-PI这4种整数阶PI控制算法，能快速地收敛到更小的适应度值。同理，从图4(b)中不难可以看出，IDE-FOPI相比GA-FOPI、PSO-FOPI、DE-FOPI这3种分数阶PI控制算法，其优化收敛过程也更为合理，最终能搜索到更优的适应度值。综述所述，IDE-FOPI相比其它7种优化控制策略能够最终获得更小的适应度值，这即意味着IDE-FOPI具有更强的搜索能力。表3为以上多种优化算法整定获得的三相逆变系统双闭环控制器最优参数。

图4 控制算法的优化迭代比较图

表3 多种优化算法整定获得的控制器最优参数

表4给出了GA-PI、PSO-PI、DE-PI、IDE-PI、GA-FOPI、PSO-FOPI、DE-FOPI、IDE-FOPI这8种不同优化控制方法下三相逆变器输出电压THD值、ITAE值和获得的最终适应度值。

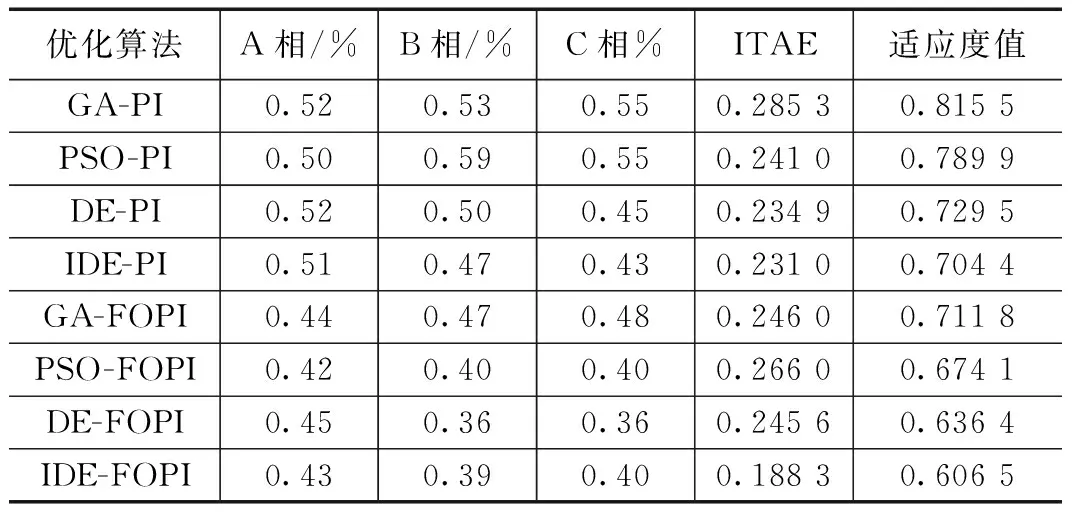
表4 不同优化控制方法下三相逆变系统输出电压THD值、ITAE值和适应度值

由表4可以看出，IDE-FOPI相比其它7种优化控制算法获得的适应度值最小(即0.606 5)，ITAE的数值也最小(即0.188 3)；IDE-FOPI算法获得的三相逆变系统A相、B相和C相输出电压的THD值分别为0.43%，0.39%和0.40%。GA-FOPI、PSO-FOPI、DE-FOPI、IDE-FOPI这4种分数阶PI控制算法所获得的三相输出电压THD值分别优于对应的整数阶PI控制算法(即GA-PI、PSO-PI、DE-PI、IDE-PI)。

另外，图5～图8分别给了在负载稳定的工况下，基于DE-PI、IDE-PI、DE-FOPI和IDE-FOPI优化控制策略的三相逆变系统输出电压波形。为了方便进一步对比观察，图9分别给出了DE-PI、IDE-PI、DE-FOPI和IDE-FOPI这4种不同优化控制策略获得的三相逆变系统输出的d轴电压波形。从图9中可以看出，相比DE-PI、IDE-PI、DE-FOPI，本文提出IDE-FOPI控制策略作用下的三相逆变系统输出电压波形动态过程的振荡最小，这意味着其动态特性更为平稳，从而进一步验证了IDE-FOPI策略在三相逆变系统控制中的优势。

图5 基于DE-PI优化控制策略的三相逆变系统输出电压波形

图6 基于IDE-FOPI优化控制策略的三相逆变系统输出电压波形

图7 基于DE-FOPI优化控制策略的三相逆变系统输出电压波形

图8 基于IDE-FOPI优化控制策略的三相逆变系统输出电压波形

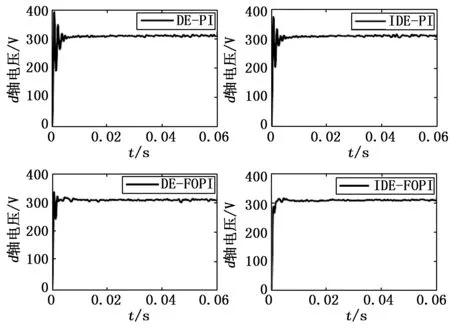
图9 几种不同优化控制策略下的三相逆变系统在旋转坐标系下的d轴输出电压

3.2 负载突变条件下三相逆变系统鲁棒性能测试

三相逆变系统的鲁棒性能也是衡量优化控制策略的重要标准。在此，本文设计如下鲁棒性能测试实验，即在0.06和0.15 s时间段分别增加并联48 Ω的电阻来模拟负载突变，从而来测试不同优化控制策略下三相逆变系统的鲁棒性能。图10～图13分别给出了DE-PI、IDE-PI、DE-FOPI和IDE-FOPI这4种不同优化控制策略作用下三相逆变系统输出电压的d轴分量。对比这4幅图，不难看出：分数阶PI控制器在应对负载突变时能够较快地恢复到稳定幅值，且基于IDE-FOPI优化控制策略的三相逆变系统输出电压的振荡过程相比DE-PI、IDE-PI、DE-FOPI更为平缓，从而验证了IDE-FOPI优化控制策略在提高三相逆变系统鲁棒性能方面的优势。

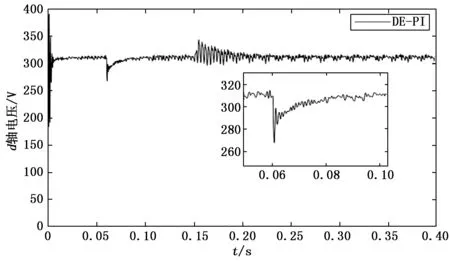
图10 基于DE-PI控制策略的三相逆变系统在负载突变时的逆变系统d轴输出电压

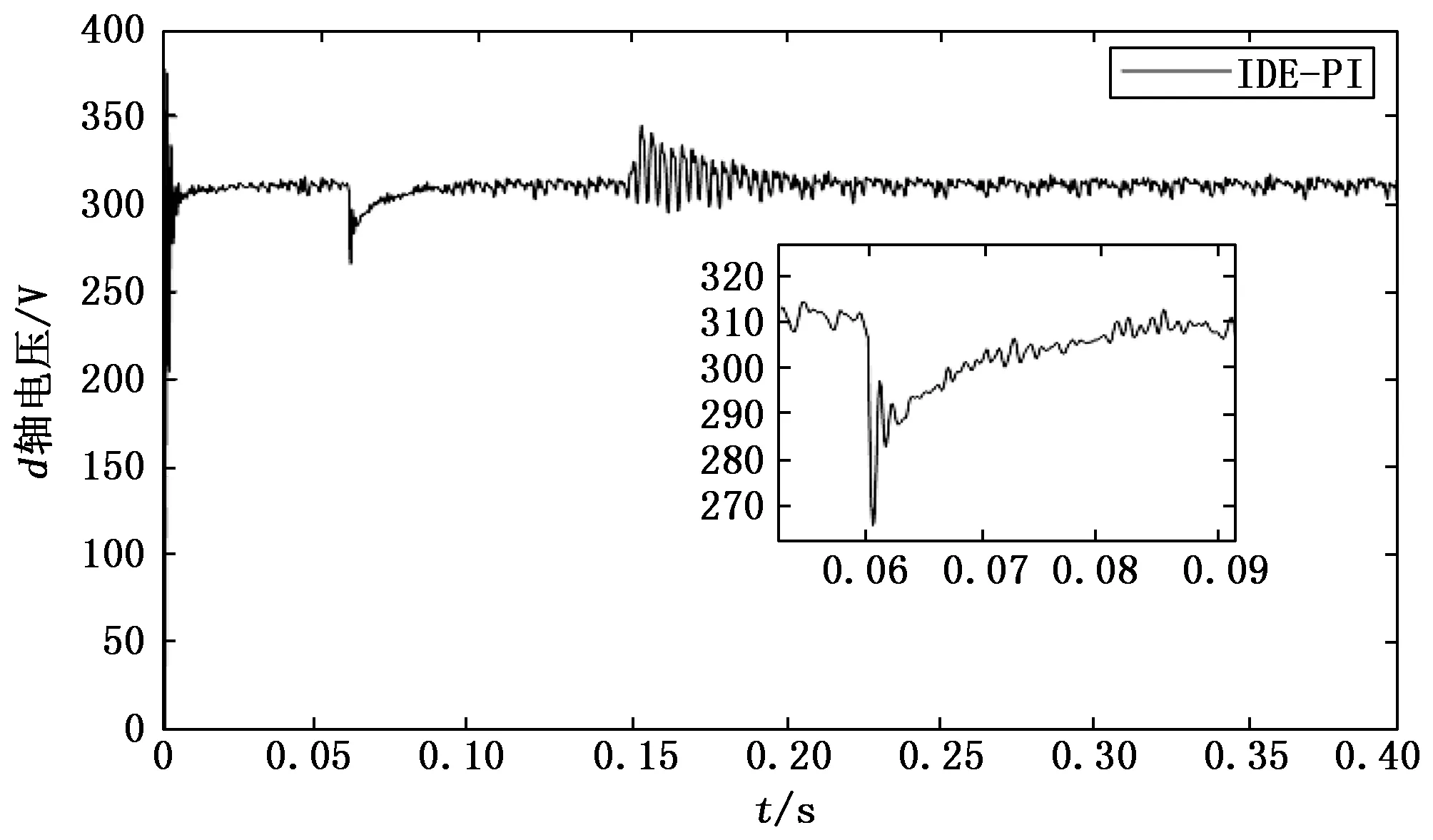
图11 基于IDE-PI控制策略的三相逆变系统在负载突变时的d轴输出电压

图12 基于DE-FOPI控制策略的三相逆变系统在负载突变时的d轴输出电压

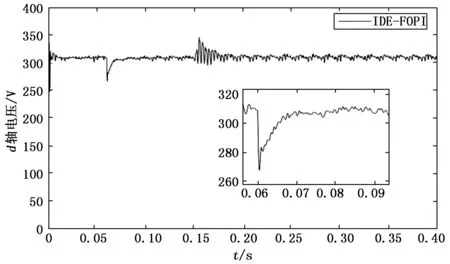
图13 基于IDE-FOPI控制策略的三相逆变系统在负载突变时的d轴输出电压

此外，图14还给出了基于IDE-FOPI控制策略的三相逆变系统在负载突变时的输出电压波形和电流波形。从所获得的三相电压波形和电流波形中可以看出：在负载突变时，系统输出的三相电压没有明显的波动，三相电流波动较为平缓，这也进一步验证了IDE-FOPI优化控制策略能够保证三相逆变系统的鲁棒性能。

图14 基于IDE-FOPI控制策略的三相逆变系统在负载突变时的三相输出电压波形和电流波形

4 结束语

针对三相离网型逆变系统传统整数阶PI控制策略控制效果不佳以及参数整定困难的问题，本文提出了一种基于改进差分进化算法的新型双闭环分数阶PI控制策略(IDE-FOPI)。本文的主要创新贡献包括：1)将分数阶微积分理论引入到三相逆变系统的双闭环控制中，搭建了dq坐标变换下三相逆变系统的双闭环分数阶PI控制模型，增加了控制器设计的灵活性，并将三相逆变系统双闭环PI控制器多参数整定问题转化为一个考虑ITAE和输出电压THD加权性能指标最小化的优化问题；2)设计了一种基于自适应多变异操作和参数自调节策略的改进差分进化算法，提高了算法的自适应和优化搜索能力，并对三相逆变系统双闭环PI控制器多参数优化问题进行了有效求解。通过与不同优化控制策略(包括GA-PI、PSO-PI、DE-PI、IDE-PI、GA-FOPI、PSO-FOPI、DE-FOPI)的仿真实验对比，验证了本文提出IDE-FOPI控制策略具有更佳的控制性能和鲁棒性能，这即验证了IDE-FOPI在三相逆变系统优化控制中的有效性。后续将进一步在三相逆变系统硬件平台进行算法性能的验证。