多目标事务模糊关联聚类的云制造服务组合算法
万年红,王雪蓉
(1.浙江东方职业技术学院 数字工程学院,浙江 温州 325000;2.浙江东方职业技术学院 教务处,浙江 温州 325000)
0 引言
云计算技术与制造业的快速融合,催生了云制造这一新型业态[1-13]。云制造过程中会产生海量的具有混杂性、异构性、用途各异、模糊性的多目标事务,它是云制造服务组合的基本单元和基本要素[4]。云制造需求、任务通过不同类型、动态演化的多目标事务匹配、组合相应的制造服务,快速响应客户需求,从而实现对制造资源的调度,缩短产品开发周期。因此,有效地对多目标事务进行分类、聚类分析[14-23],识别多目标事务的相似性及差异性,从而有效地实现云制造服务组合的目标是一个热点问题。
目前,关于云制造服务组合的研究方法已受到了学者关注,例如:SLA感知的事务型组合服务容错方法[1]、基于事务的分布式虚拟化环境下服务替换方法[2-3]、基于动态匹配网络的制造服务组合自适应方法[4-5]、基于区间的制造服务组合多目标优化方法[6]、基于双层蚁群算法的云制造服务组合方法[7]、基于协同效应的并行制造云服务组合算法[8]、云制造模式下面向加工设备的服务聚类与初选方法[9]、云制造环境下的知识服务组合优化策略[10-11]、基于组合历史的交互式服务推荐方法[12]、时空敏感的QoS预测方法[13]等。这些方法采用向前或向后恢复策略针对云制造服务组合的失效和QoS(quality of service,服务质量)的变化更新,对多目标事务进行处理,对已执行的事务进行补偿,准确预测备选服务的QoS,在线选取、实时处理多种不同类型事务的动态服务组合方案,克服了服务组合负载能力不足的问题,提高了对动态云制造多目标事务的应变能力和服务组合执行的可靠性、稳定性和一致性,较好地实现了云制造服务组合的目标[1-13]。因此以上方法均具有一定的借鉴意义。但是,在云制造模式下,事务通常是混杂、异构、不确定、多目标、动态演化的,仅从以上方法的角度来研究云制造服务组合,存在着只依赖于定期挖掘的初始数据和日志导致额外开销,不能适应服务组合的动态更新、负载均衡和服务队列依赖关系,不能考虑需求和服务之间的变更等问题[1-13],在云制造服务组合的收敛性、平稳性、敏捷性、动态演化性、智能性等方面,效果明显不能达到要求。
实际上,随着云计算技术的发展,目前云制造的相关标准、架构较为统一、成熟[1-13],多目标的云制造事务之间一般都具有看似非线性、离散、混沌、异构但可以通过模糊理论和概率论处理得到一定程度相关的多目标事务模糊关联维属性,如果综合模糊聚类和关联聚类分析方法[14-19],结合概率论、遗传算法就可以把看似混沌、不关联的多目标事务模糊关联维属性提取出来,基于此,可以较好地将模糊、混沌的云制造多目标事务有效划分到相应聚类中心,使得云制造空间中多目标事务具有簇间差异化分组和簇内相似性分组,再通过集成机制实现云制造服务的全局组合。但是由于云制造环境的高度混杂性和动态演化性,从实际的聚类效果来看,以上传统方法存在端到端QoS约束、制造服务组合变更率、制造任务变更率、制造服务组合执行成功率、制造服务组合负载均衡度、制造服务组合负载队列优化能力、制造服务组合最大负载低[1-13]等需要解决的关键问题,关于多目标事务模糊关联聚类的云制造服务组合算法的更有效的研究并不多见。
因此,本文针对上述研究的不足,基于多目标事务模糊聚类,改进相关算法,开展多目标事务的云模式通用解析、多目标事务模糊关联特征的云模式通用表示、云制造服务组合多目标事务模糊关联聚类算法等方面研究,设计一种敏捷、智能、平稳的云制造服务组合算法(SCACM,service composition algorithms in cloud manufacturing based on fuzzy correlation clustering of multi-objective transactions)。
1 基于云模式的制造服务组合问题描述
1.1 多目标事务的云模式通用解析
本文因篇幅所限,关于云和云滴的通用定义,请读者参见文献[4-10]。
定义1:云制造多目标事务。
云制造多目标事务是指云制造过程中在一个非线性时间间隔内,有多个云池IP地址发出的非线性、任意形态、不同密度、用途各异的云制造事件序列。
由于云制造任务通过不同类型、动态变化的多目标事务组合相应的制造服务,因此,首先要对云制造多目标事务进行云模式通用解析。
假设:在制造需求下,在一个表示定量论域的有限变量集LD={LDi|i∈N}的约束下,一个事务Transi是由制造请求URi、事务编号TNi、事务地址IPi、事务粒度TLDi、事务组件TZJi、事务初始状态TCZi、事务迁移状态TRFi、事务结束状态TEZi、制造Web日志WRZi、制造最低兴趣度ZDXi、时间间隔TGi等事务单元TWDi组成的集合,即Trani={URi,TNi,IPi,TLDi,TZJi,TCZi,TRFi,TEZi,WRZi,ZDXi,TGi}。采用穷举搜索算法[1],对TCZi、TRFi、TEZi进行赋值,将任意形态、不同密度、异构的TZJi的串行执行顺序改进为并行选择,作为定性概念TWDi的一次随机实现,且把TGi看成是有稳定倾向的随机数,在其解空间中,随机、均匀地产生URi、TNi、IPi,且当TGi→[0,1],对∀TLDi,TZJ,都有WRZi∈LD,ZDXi∈LD,改进每个事务单元TWDi的N维状态机向量XL(i)=〈xl(1),xl(2),…,xl(i)〉,若对∀TWDi,都有XL(i)→TCZixTRFixTEZi,且满足TLDi=LDi,TZJi=LDi,则称Transi在论域LD上的分布称为云,记为Tre(i),URi,TNi,IPi址,TLDi,TZJi,TCZi,TRFi,TEZi,WRZi,TGi称为云滴,记为Tred(i)。
根据以上定义,多目标事务的云模式通用解析函数如式(1)所示:
(1)
式(1)根据文献[4-10]中关于云和云滴的通用定义,改进事务组件TZJi的串行执行顺序为并行选择,可以在非线性、不可微、离散的云制造空间中全局寻优多目标事务,并通过Tre(i)、Tred(i)改进、映射到N维状态机向量XL(i),从而实现了云制造多目标事务的云模式通用解析。
1.2 多目标事务模糊关联特征的云模式通用表示
定义2:多目标事务模糊关联特征。
多目标事务模糊关联特征是指云制造空间中看似非线性、离散、混沌、异构但可以通过模糊理论和概率论处理得到一定程度相关的多目标事务模糊关联维属性。
多目标事务模糊关联特征是实现多目标事务模糊关联聚类以及基于此的云制造服务组合的关键。因此,需要对多目标事务模糊关联特征进行云模式通用表示。

(2)
1.3 云制造服务组合问题

2 云制造服务组合多目标事务模糊关联聚类算法
定义3:模糊关联聚类。
模糊关联聚类是指基于定义1、定义2、式(1)、式(2),运用模糊聚类和关联聚类方法对应用于云制造服务组合的多目标事务进行聚类分析,目的是使得云制造空间中多目标事务具有簇间差异化分组和簇内相似性分组。
多目标事务模糊关联聚类是云制造服务组合的关键,其算法步骤如下:
步骤1:设定云滴影响因素的第k个聚类样本的第i个特征在TGi时刻的数值,把制造Web日志WRZi随机分成N个事务粒度TLDi,为第i个TLDi的每个模糊关联特征权重赋值为1,设定多目标事务模糊关联特征决策方案集S={si|i∈N},根据经验贝叶斯方法[15],初始化第i个TLDi的聚类中心点Ci,并使FCPH(Transi)各指标具有不同的云滴量纲和属性,计算当前各聚类中心点Ci的模糊隶属度加权和wi,得到模糊关联特征提取矩阵FEZJi,创建(N+TGi)维权重向量WXLi,使TLDi的模糊特征绝对量之间的关联距离disAi最小化,可得如式(3)所示的模糊关联特征序列的提取函数:
(3)
通过式(3),加速搜索以概率出现的聚类中心参数与实际值的波动距离,初始化云滴模糊关联特征样本矩阵,用来控制聚类中心的紧致度,从而实现多目标事务模糊关联特征的提取。

(4)
根据式(4),生成多目标事务的新建议样本,找到局部最优解,进一步筛选出更适合聚类的模糊关联特征的代表点事务对象。
步骤3:采用优选元胞遗传模糊聚类方法[16],以当前马尔科夫链状态为中心,利用正向云[4-10],以云滴相互迭代方式来优化聚类目标事务Transi,通过设定模糊隶属的最小约束ZXYSi,确定存在两种情况:肯定属于聚类中心的集合CCi={cci|i∈N}和一定不属于聚类中心的集合CNi={cni|i∈N},即聚类应用于云制造服务组合的多目标事务时固定一个变量xi,按式(5)所示的模糊隶属度函数计算代表点事务对象模糊隶属度,求解得到多目标事务模糊关联特征的模糊聚类簇。
(5)

(6)
通过式(6),在模糊因子[14-16]约束下,将所有代表点事务对象都当成向聚类中心Ci靠拢的云滴代表点,可以获取每个视角下的时空关联轨迹跟踪矩阵,动态、实时地实现多目标事务对象检测点之间的关联。
步骤5:采用粒子群优化算子[16],对式(6)实施动态交叉和两阶段变异,消除多目标事务对象代表点的差异性,反复迭代,使得具有代表点事务对象模糊隶属度、代表点事务对象时空关联度最大值的事务对象向聚类中心Ci靠拢,从而将代表点事务对象划分到相应的聚类簇,最终实现面向云制造服务组合的多目标事务的模糊关联聚类。
3 基于相关算法改进的SCACM算法设计与建模
3.1 反向学习算法的改进
反向学习算法[8-9]是SCACM算法的关键。但传统的反向学习算法在对比当前概率样本之间的似然值时,组合概率受到隶属度参数向量不规则影响,未能使关联距离disAi和增速距离ZDISi之间的误差最小化,从而影响了对QoS的评估。因此,有必要对反向学习算法进行如下改进:
假设当检测到多目标事务处于未更新云滴状态时,改进反向学习函数[8],即将第k个聚类样本的模糊关联特征在t时刻的属性值,引入到原始事务对象的权重YWi和代表点事务对象的权重DWi中,启动下一次迭代中的反向学习过程,剩下的簇中代表点事务对象在回归系数HGi的约束下,准备转至下一个云节点CJDi,将反向学习函数运用到每个云滴节点CJDi的路径选择中,并在聚类中心点Ci的模糊隶属度加权和wi的影响下,逐步向聚类中心Ci靠拢,并行实施任意两个云滴节点之间不同服务的协同效应,从而可以得到较好的制造服务组合。
改进的反向学习函数形式如式(7)所示:
(7)
式(7)改进的主要贡献在于:将改进的聚类样本模糊关联特征属性值引入YWi和DWi,在迭代中的反向学习过程约束概率样本似然值,可使不同视角下的对应样本获得相同的聚类标签,保持一致的标签编号,使得disAi和ZDISi误差最小化,从而解决组合概率不规则问题,从而可以准确评估QoS。
3.2 可替换服务推荐算法的改进
可替换服务推荐算法[7,12]是SCACM算法的关键。但传统的可替换服务推荐算法在更新云滴节点时只考虑将新加入的边和受影响的边加入到制造服务组合中,当云分布符合幂分布时,存在“无标度”服务的问题,仅仅依靠多目标事务间的相似度进行服务的划分和服务协同推荐,未能“择优”进行制造服务组合。

基于云节点的加权度函数的改进形式如式(8)所示:
JQDH(Transi)=
(8)
式(8)改进的主要贡献在于:通过不断地交互构造,从并行处理角度分析未选择服务WXSi和已选择服务YXSi节点的重要性,考虑将新加入的边和受影响的边加入到制造服务组合中,忽略服务替换上的差异值得到真正需要的组合方案,“择优”进行制造服务组合,得到相似服务集,实现多目标事务服务的协同推荐。
3.3 SCACM算法设计与建模
根据多目标事务的云模式通用解析函数、多目标事务模糊关联特征的云模式通用表示函数、云制造服务组合多目标事务模糊关联聚类算法和改进的反向学习算法、可替换服务推荐算法,设计敏捷、智能、平稳的云制造服务组合算法。
SCACM算法模型如图1所示。
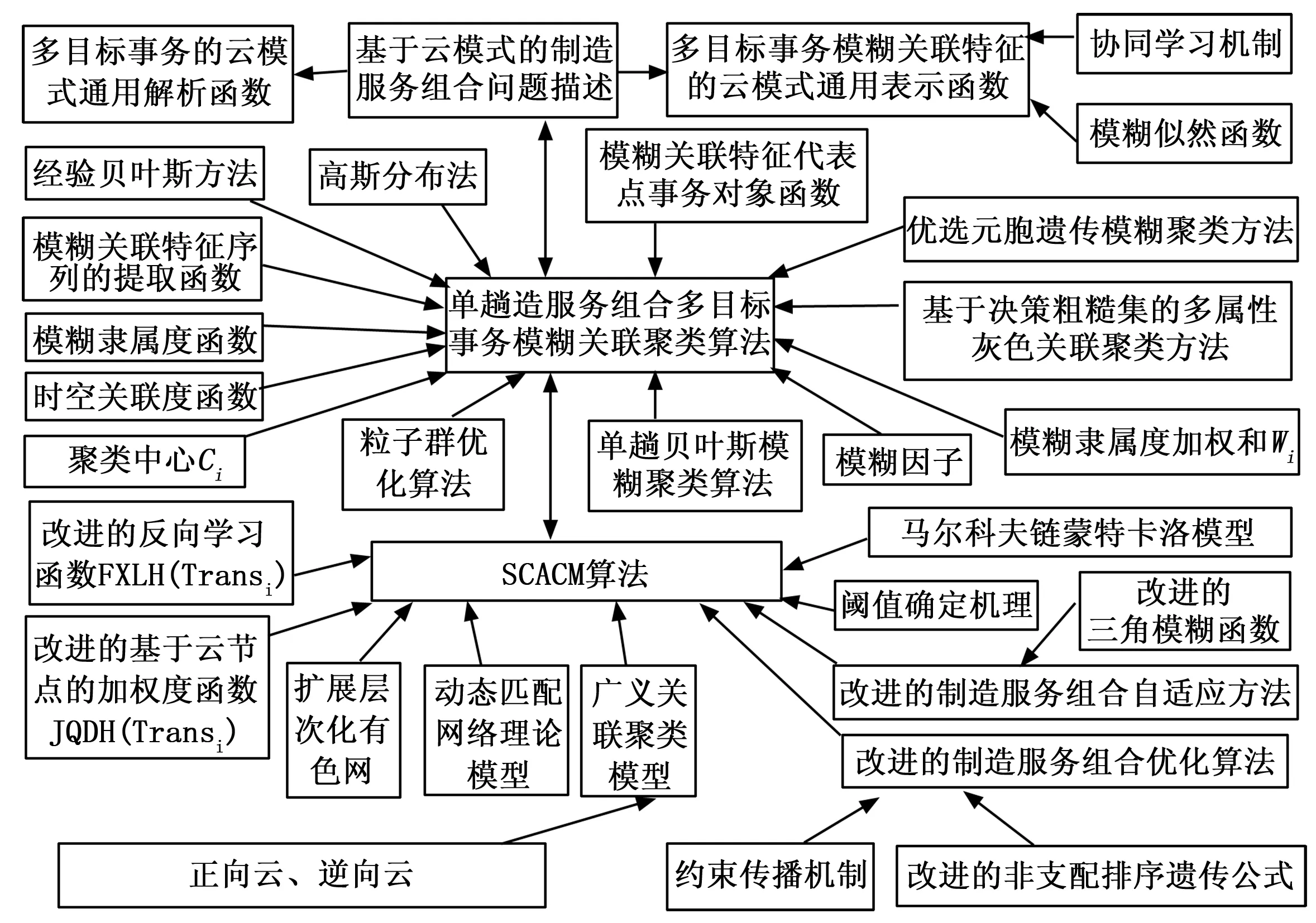
图1 SCACM算法模型
SCACM算法步骤如下:
步骤1:基于式(1)、式(2),根据云制造事件序列,采用扩展层次化有色网[2],通过Tre(i)、Tred(i)改进、映射到N维状态机向量XL(i),准确描述组合服务中层次结构及控制关系,使得云制造空间中多目标事务的模糊关联特征具有一致性分布,构建服务组合的组件及其消息交互模型,从而对云制造多目标事务进行云模式通用解析和对多目标事务模糊关联特征进行云模式通用表示。
步骤2:基于式(3),采用动态匹配网络理论模型[4],构造制造任务网络和制造服务网络,以动态优化QoS为目标,创建(N+TGi)维权重向量WXLi,加速搜索以概率接受的聚类中心参数与实际值的波动距离,根据不同类型的制造服务变更,将最优制造服务组合问题转化为制造服务网络中最短路径的搜索,初始化多目标事务模糊关联特征样本矩阵,控制云滴的紧致度,用于表达制造服务与制造任务之间的动态匹配关系,从而实现模糊关联特征的提取。
动态匹配网络理论模型可用如式(9)所示的函数表示:
(9)

马尔科夫链蒙特卡洛模型可用如式(10)所示的函数表示:
(10)
步骤4:基于式(10),采用制造服务组合自适应方法[4]对筛选出的模糊关联特征的代表点事务对象进行变更预处理、动态调度,完成事务对象间云滴匹配边的更新。但是,传统制造服务组合自适应方法只计算事务对象在某一个时刻的动态匹配,缺乏对事务对象的全程匹配的描述,比较难适应动态多变的云制造环境,它实际上是一种静态调度方法。因此,需要对传统的制造服务组合自适应方法做如下改进:
假设:根据任务序列(A1→A2→A3→A4),改进三角模糊函数,即分别用P1、P2、P3、P4表示任务序列多目标事务的执行成本、执行时间、执行状态、执行质量,确定当前最优的多目标事务的增加、删除和修改,然后按照绑定的模糊聚类方案一步步执行,实现多目标事务的更新,在P1、P2、P3、P4区间规划中,其云滴数序关系可用左隶属度函数LLSD(i)和右隶属度函数RLSD(i)来定性地表示,并在模糊因子的约束下,根据当前云滴环境调用绑定多目标事务,若需增加事务节点Transji,则在当前执行区间中更改执行状态P3为待执行状态,通过判断左隶属度和右隶属度之间的优劣,将P1、P2、P4修改为最优形式。
三角模糊函数的改进形式如式(11)所示:
SJFH(Transi):
(11)
式(11)改进的主要贡献在于:将多目标事务属性转换成易于识别的三角模糊数形式,并进行规范化处理,然后按照绑定的模糊关联聚类方案一步步执行,对筛选出的模糊关联特征的代表点事务对象进行更新更、动态调度,在得到每个目标事务的同时获得模糊关联特征的最优解,从全局上对事务对象的匹配过程进行描述,并将不确定的多目标事务优化为两个确定性的左隶属度函数LLSD(i)和右隶属度函数RLSD(i),从而为多目标事务模糊关联特征的模糊聚类簇打下基础。
步骤5:基于式(5)、式(10)、式(11)采用广义关联聚类模型[18],以相互迭代的方式来优化聚类目标事务Transi,融合模糊关联特征的代表点事务对象检测点和轨迹片段,利用逆向云[4-10],设定最小约束ZXYSi来确定表示事务A和事务B之间的结构关系权重并固定为一个变量xi,计算多目标事务对象代表点的模糊隶属度,求解并行服务的协同效应值,作为云滴启发函数参数,得到多目标事务模糊关联特征的模糊聚类簇。
广义关联聚类模型可用如式(12)所示的函数表示:
(12)
步骤6:基于式(6)、式(12),采用阈值确定机理[17],对多目标事务模糊关联特征的模糊聚类簇进行优选,通过引入两个阈值参数θi1、θi2,定义多目标事务对象代表点间的可能关系和集合,确定模糊关联特征的代表点事务对象关联度似然值的增速距离ZDISi,替换为灰色关联聚类的非此即彼结构,使之呈现不同类型和属性权重的代表点事务对象时空关联问题。
阈值确定机理可用如式(13)所示的函数表示:
(13)
约束传播机制可用如式(14)所示的函数表示:
(14)
步骤8:基于式(14),采用制造服务组合优化算法[6]进行云制造服务组合优化。但是传统的制造服务组合优化算法受制造资源自身条件的所限,存在多目标事务之间互斥性与可信度不高的问题,限制了服务执行队列和等待队列的长度,一般只能获取一组非支配解,可靠性、能耗最小化未必能得到保证。因此,需要对传统的制造服务组合优化算法进行如下改进:改进非支配排序遗传公式,即设定多目标事务对象候选代表点的制造工艺路线,初始化表示任务要求的加工的零件或毛胚数量(种群规模)ZQGMi、最大能耗交叉概率为RSTJi、成本变异概率为RSTBi,从满足要求的候选模糊关联特征云滴资源池中,随机产生一个初始种群ZQGMi(x),执行子任务候选云服务编号,并按照可执行加工顺序组合云服务,通过选择、交叉、变异等操作得到最佳工艺路线,最后,从合并后的候选工艺路线中依序选择M个ZQGMi(x)个体进入下一次迭代,并在服务调用过程中保持服务时间不变,按照拥塞度比较RSTJi和RSTBi,若RSTJi和RSTBi保持稳定不变,则认为云制造服务组合得到了优化。
非支配排序遗传公式的改进形式如式(15)所示:
(15)
式(15)改进的主要作用在于:解决了云制造服务组合优化过程中多目标事务聚类的运算速度慢、稳健性低、鲁棒性低、离散性、互斥性与可信度的问题,可以对非支配关系执行快速的排序,可靠性、能耗最小化得到了保证,进而得到服务组合目标的最优解。
步骤9:基于式(15),采用式(7)改进的反向学习函数,引入原始事务对象的权重YWi和代表点事务对象的权重DWi,根据多目标事务模糊关联维属性搜索的结果,动态分步绑定服务组合,当服务组合执行队列处于空闲状态时,启动下一次迭代中的反向学习过程,并在聚类中心点Ci的模糊隶属度加权和wi的影响下,服务组合等待队列进入执行状态,逐步向聚类中心Ci靠拢,合理调度云滴资源,实现各制造服务云滴节点负载均衡,并行实施任意两个云节点之间不同服务的协同效应,从而将不同类型、动态变化的多目标事务匹配、组合到相应的制造服务。
步骤10:基于式(7),采用式(8)改进的可替换服务推荐算法,基于最短路径算法从并行处理角度分析未选择服务WXSi和已选择服务YXSi节点,从云制造服务网络中选出满足制造任务约束代价最小的服务组合,并将向初始聚类中心靠拢的敏感度MGDi和局部极值JBJZi划入可替换服务集KTHFi,将模糊关联的制造服务动态绑定,得到相似云滴服务集,通过不断地迭代过程,自动为下一个服务寻找合适的聚类中心,“择优”实现多目标事务服务的协同推荐,反复地将具有模糊关联特征的所有服务都归入同一个制造服务组合集合中,从而最终实现多目标事务模糊关联聚类的云制造服务组合。
至此,算法结束。
4 实验验证
4.1 实验数据收集与算法性能参数指标
根据SCACM算法及图1模型,所有的实验验证结果均选用Tomcat7.0为Web服务器,使用Matlab软件来仿真求解。实验数据来自电信Hadoop云平台中关于飞机制造的10 000余条任意形状、不同密度、离散的云服务历史数据,数据收集的截止时间为2022年3月31日,并采用数据分解方法[4]对数据降噪、减维、规范格式,得到平面直角坐标系中7个并行的机身制造、机翼尾翼制造、起落架制造、发动机引擎制造、航空电子系统制造、机载设备制造和其他零部件制造服务组合的点云数据。
通过对文献[1-18]的分析,归纳出评价算法性能的8个参数指标,如表1所示,其计算公式按从上到下的顺序分别用式(16)~(23)所示的公式表示(具体推导过程见文献[1-18]):
PJDL(Transi)=FZPYH(Transi)θi1-ZQGMiθi2
(16)
QoSS(Transi)=
PJDL(Transi)θi1-RSTBiP⊕JDL(Transi)θi
(17)
ZZFR(Transi)=PJDL(Transi)+QoSS(Transi)α
(18)

(19)
(20)
(21)
FZDLY(Transi)=
(22)
ZZFZD(Transi)=
(23)
由于式(16)~式(23)没有考虑权重系数约束的影响,可能导致与真实结果出现偏差,因此需要进一步采用面向时间的优化模型[6]、模糊互补判断矩阵权重公式[7]、有效性度量方法[8],通过一个统一的加权赋值函数对评价算法性能的8个参数指标的值进行加权赋值,融合计算误差,确定算法性能参数指标值的有效区间(具体推导过程见文献[6-8]),见表1所示。

表1 算法性能参数指标设置[4]
加权赋值函数如式(24)所示:
JQFZ(Transi)=FZJHD(Transi)wi+ZZFZD(Transi)θi2-

(24)
4.2 实验设计和结果分析
实验从3个方面来实施:验证改进算法的性能优势;验证SCACM算法敏捷性优势;验证SCACM算法智能性和动态演化性。
4.2.1 改进算法的性能分析
1)实验过程与结果:
步骤1:采用面向质量的优化模型[6],设定质量约束值,引入多目标事务的权重YWi和模糊关联特征的权重DWi,其综合质量不低于允许的最低评价值,若所有制造
子任务均选择转至下一个云节点CJDi,应当考虑选用权重系数较小的服务进行组合,使得disAi和ZDISi误差最小化,从而验证式(7)的性能优势。
步骤2:采用面向成本的优化模型[6],通过不断地交互构造多目标事务,设置候选制造服务的执行成本矩阵,优化面向成本的多目标事务,将向初始聚类中心靠拢的敏感度MGDi和局部极值JBJZi划入可替换服务集KTHFi,最小化服务组合的总体执行成本,得到真正需要的组合方案,统一表示为区间数或模糊关联数,“择优”进行制造服务组合,实现多目标事务服务的协同推荐,从而验证式(8)的性能优势。
步骤3:采用核密度估计方法[22],按照绑定的模糊关联聚类方案一步步执行,保证加工顺序满足要求并在模糊因子的约束下,通过判断左隶属度和右隶属度两个区间数之间的优劣,实现动态变化的协同效应最大化,通盘考虑顺序、并行、选择、循环等各种组合结构,将不确定的多目标事务优化为两个确定性的LLSD(i)和RLSD(i),寻求最优的基于模糊关联聚类的服务组合,从而验证式(11)的性能优势。
步骤4:采用服务组合优选法[8],按云制造服务的产品级粒度,通过选择、交叉、变异等操作得到ZQGMi、RSTJi、RSTBi最佳工艺路线,并分解为能够被完成的子服务,依序选择M个ZQGMi(x)个体进入下一次迭代,追求最大化的服务组合协同效应,进而得到服务组合的最优解,从而验证式(15)的性能优势。
为消除容易陷入局部最优解导致的数值差异的问题,实验次数设定为100次,每次实验的迭代次数依次递增1(从1开始)。因此,算法改进前后的性能指标值以通过对式(16)~式(23)多次计算后的平均值形式来衡量,以式(24)加权赋值函数进行加权赋值,融合计算误差,并按式(25)所示的无量纲处理方差函数[7]来将实验结果归一化到区间为[0,1](具体推导过程参见文献[1-18])。算法改进前后的性能对比如图2所示。

图2 算法改进前后的性能对比
(25)
2)改进算法性能可行性分析:
由图2可知:算法改进前后的性能指标的平均值经过式(25)无量纲处理方差函数处理后均落在归一化区间为[0,1]。但是改进前的算法曲线呈现不规则的变化规律,波峰和波谷起伏较大,这说明改进前的算法平稳趋势不明显,原因在于端到端QoS约束系数和制造服务组合最大负载低、不能较好地适应吞吐量变化,收敛速度慢,容易陷入局部最优解,导致最优解空间小,收敛的偶然性比较大、概率比较低。然而,即使经过多次实验、多次迭代,改进后的算法曲线呈现规则的变化趋势,波峰和波谷起伏的相位相差很小,使得多目标事务的disAi和ZDISi误差最小化,这说明收敛速度快,没有出现数据混乱和丢失的情况,将向初始聚类中心靠拢的敏感度MGDi和局部极值JBJZi划入可替换服务集KTHFi,可以避免局部最优解、得到全局最优解,寻求最优的基于多目标事务模糊关联聚类的服务组合。因此验证了算法改进的有效性。
4.2.2SCACM敏捷性分析
基于云服务集合的初选方法[9],建立云服务请求与服务类簇的物元模型,以相互迭代方式来融合模糊关联特征的代表点事务对象检测点和轨迹片段;采用项目协同方法[9]校正指标数值,求解并行服务的协同效应值,分析最大属性值和最小属性值差异,确定模糊关联特征的代表点事务对象关联度似然值的增速距离ZDISi和服务的相似性度量,在和α约束下使得模糊隶属度最优解限定在可以接受的范围内,使得对不同云制造服务属性评价的高低趋势一致,动态、实时地实现多目标事务对象检测点之间的关联。反复迭代,通过映射函数传播至其他视角以进行协同学习,从而验证SCACM算法的敏捷性优势。
其中敏捷性以制造任务平均到达速率、制造服务组合变更率来衡量,分别通过式(16)、式(18)来计算。实验次数设定为150次,每次实验的迭代次数依次递增1(从1开始),计算结果以平均值形式来衡量,以式(24)加权赋值函数进行加权赋值,融合计算误差。通过与文献[4]、文献[6-9]、文献[12]提出的算法的对比,敏捷性验证结果如表2所示。
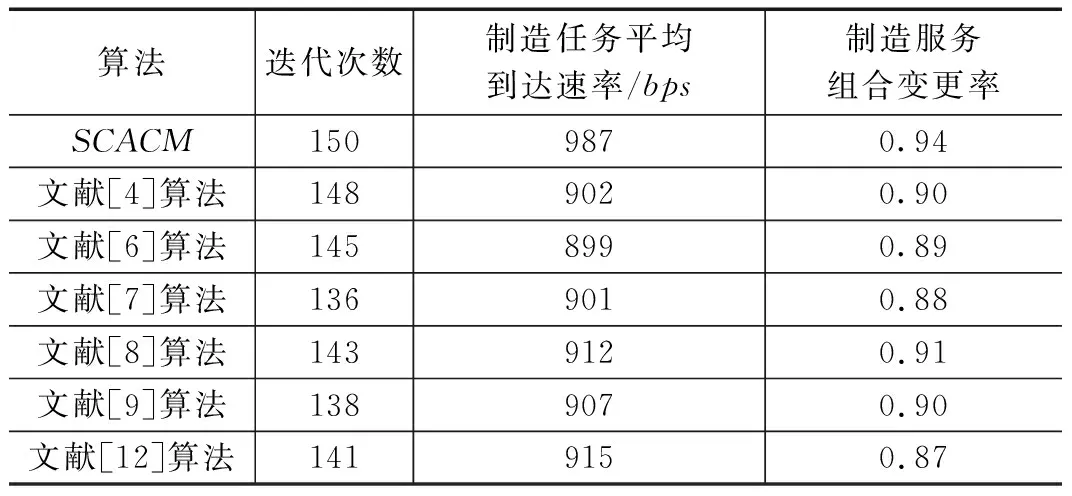
表2 SCACM算法敏捷性验证结果
表2结果表明:各种算法的制造任务平均到达速率、制造服务组合变更率均符合预定的要求。相比传统算法,SCACM以相互迭代方式来优化聚类目标事务Transi,能够增强组合服务之间的协同合作与反馈,以最小约束ZXYSi来确定表示事务A和事务B之间的结构关系权重,随着制造任务平均到达速率的增加,多目标事务模糊关联聚类的时间周期越短,通过引入的阈值参数θi1、θi2定义多目标事务对象间的可能关系和集合,制造服务组合变更率表现出相同的变化趋势,多目标事务模糊关联聚类簇内组合服务间关联程度越大,使之呈现不同类型和属性权重的代表点事务对象时空关联问题,仅仅产生幅度不大的波动,响应时间、响应速度都比较满意,云制造任务发送到云制造服务组合的平均速率、云制造需求平稳转换为制造任务的比率高,可快速准确地得到云制造服务组合的QoS和协同效应值,从而快速响应全局最优解的求精过程。因此验证了SCACM算法的敏捷性优势。
4.2.3SCACM智能性和动态演化性分析
1)实验过程与结果:
采用累计概率密度函数[23],准确描述组合服务中层次结构及控制关系,剔除影响多目标事务的模糊关联特征一致性分布的消极指标和局部学习因素,以动态优化QoS为目标,创建(N+TGi)维权重向量WXLi,设定智能交叉因子和动态演化变异因子为0.14和0.32,比较每一个模糊关联特征样本矩阵隶属度向量LSDXLi的接受率和累积概率密度曲线,从全局角度动态设定制造任务节点和制造服务节点的时间状态属性,在不考虑开销的情况下,动态调整各个子任务的影响差距,并将云制造多目标事务关联度阈值设置为θi,智能分步组合制造服务,从而验证SCACM算法的智能性和动态演化性优势。
其中智能性和动态演化性主要以制造任务变更率、制造服务组合执行成功率、制造服务组合负载均衡度、制造服务组合负载队列优化能力来衡量,分别通过式(19)~式(22)来计算。计算结果以平均值形式来衡量,以式(24)加权赋值函数进行加权赋值,融合计算误差。
由于云制造环境的复杂性,在服务组合的过程中,不同的实验过程总会产生难以避免的噪音干扰,因此,为了尽量减少噪音干扰,还需采用如式(26)所示的噪音过滤函数来过滤噪音(具体计算过程见文献[1-18])。

FWZHC(Transi))-WLGF(Transi)TGi
(26)
通过与文献[4]、文献[6-9]、文献[12]提出的算法的对比,SCACM算法智能性和动态演化性验证结果见表3所示。噪音过滤曲线如图3所示。
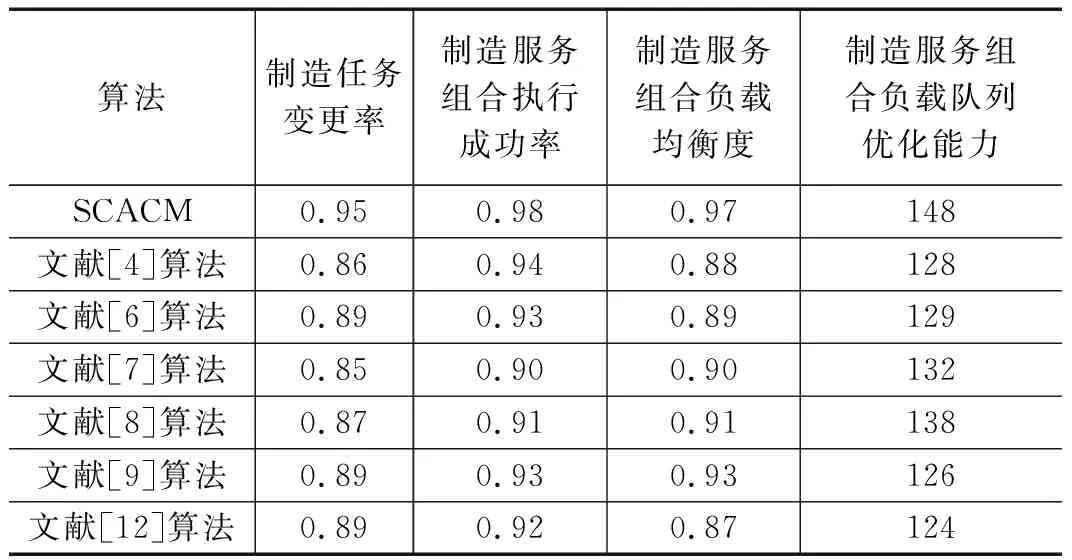
表3 SCACM算法智能性和动态演化性验证结果

图3 噪音过滤曲线
2)智能性和动态演化性可行分析:
分析表3、图3可知:随着实验次数和迭代次数的增加,噪音过滤曲线呈现递增趋势,表明通过式(26)所示的噪音过滤函数,最大程度地过滤了噪音,制造任务变更率、制造服务组合执行成功率、制造服务组合负载均衡度、制造服务组合负载队列优化能力等性能指标的平均值受噪音影响较小。因此在尽量减少噪音的情况下,各种算法的制造任务变更率、制造服务组合执行成功率、制造服务组合负载均衡度、制造服务组合负载队列优化能力均符合预定要求。相比传统算法,SCACM算法从云制造服务组合的协同效应角度出发,能自动调整模糊关联特征的多目标事务对象代表点,使服务组合的优势放大,将模糊指数约束于[0.5,1]区间,服务组合的接受率更高,在累积概率密度曲线和模糊置信度为FZXDi的指引下,在解空间内搜索到最优解的概率大,在事务粒度种群数不变的情况下,通过增大特征样本关联度的似然值,云制造需求平稳转换为制造任务的比率大,实时更新制造任务网络和制造服务网络,制造服务组合执行成功率、多目标事务模糊关联聚类簇间区分度和服务组合精度高,云制造服务各节点制造资源局部优化的协同过滤程度高,云制造服务各节点制造资源全局负载队列的优化程度高,表达了制造服务与多目标事务之间的动态匹配关系。因此,SCACM算法具有较高的鲁棒性、动态演化性和智能性。
5 结束语
云制造是目前的一个重要研究课题,其海量的具有混杂性、异构性、用途各异的多目标事务具有可聚类的模糊关联特征,是云制造服务组合基本要素。本文基于多目标事务模糊关联聚类提出的云制造服务组合算法,在制造任务平均到达速率、端到端QoS约束系数、制造服务组合变更率、制造任务变更率、制造服务组合执行成功率、制造服务组合负载均衡度、制造服务组合负载队列优化能力、制造服务组合最大负载等关键性能指标上均符合预定的要求,因此SCACM算法具有一定的实用价值。但是,鉴于云制造非常复杂,云制造服务组合实际上受软件、硬件、网络环境、云计算平台的限制,效率未必是最优的,本文提出的SCACM算法只是一个参考模型,在许多方面还有待作者进一步深入研究。

