高斯过程回归的近似方法及其应用

张明民

(同济大学 中德学院，上海 201804)

0 引言

建模方法一般可以分为参数建模和非参数建模。参数建模适用于为较简单的系统构建模型，通常要求系统结构可以用已知的数学模型来描述，再确定模型中的未知参数即可实现建模。然而，对于复杂的非线性系统的建模则需要非参数模型。数据驱动的非参数建模方法不受模型结构的限制，其适用范围更广，并且只需要很少的先验信息就可完成高质量的建模[1]。在当今的信息社会，众多应用场景中都可以提供大量的可用数据，这大大促进了非参数建模的发展。非参数建模方法的灵活性和强大的模型表达能力让其在各个领域被广泛应用，例如工业处理[2]，生物工程[3]，自主机器人[4]和无人机[5]的控制等。

非参数建模方法之一是高斯过程回归 (GPR)，它一般用于非线性函数的建模[6]。作为一种贝叶斯机器学习方法，GPR与神经网络的联系在于，许多基于神经网络的贝叶斯回归模型在网络无限大的情况下会收敛为高斯过程(GP)[7]。GPR可以根据训练数据调整模型的复杂度，还能以一定概率保证预测误差的有界性[6]，使其能被应用于对安全性要求较高的场景。尽管有以上这些优点，但是它的计算复杂度随着训练数据的增加急剧增长。具体来说，对于n个训练样本，GPR的更新和预测时间复杂度分别为Ο(n3)和Ο(n2)，过高的计算成本使GPR无法被用于很多大数据量的学习任务。为此，一些近似方法被开发出来，以通过近似计算代替精确计算来减少GPR的计算量，如选取一部分有代表性的数据来代替整个数据集。

本文在说明GPR原理的基础上，详细分析了其近似方法，并介绍了其在一些领域的应用情况。

1 高斯过程回归简介

高斯过程是一个随机变量的集合，任意有限数量的这些随机变量的组合都具有联合高斯分布[6]。一个GP由其均值函数和协方差函数完全确定。

作为一种机器学习方法，GPR需要训练数据。假设数据集{X,y}由n对数据构成，其中输入集X={x1,x2,...,xn}由n个输入向量组成，而输出集y={y1,y2,...,yn}由n个对应的一维输出组成。

对于一个问询点x，它对应的输出f(x)是一个GP，其先验均值和方差由下式给出:

μ(x)=E[f(x)]

(1)

k(x,x′)=E[(f(x)-μ(x))(f(x′)-μ(x′))]

(2)

通常假设均值为0，故f(x)可以表示为:

f(x)～N(0,k(x,x′))

(3)

y是对f(x)的受到干扰的观测：

yi=f(xi)+εi,i=1,…,n

(4)

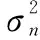
(5)

(6)

其中：I是单位矩阵，K(X,X)是n×n维的GP协方差矩阵，由元素Kij=K(xi,xj),i,j=1,…,n组成。K(X,x)是输入集X中所有的元素xi(i=1,…,n)分别与问询点x所求得的协方差组成的协方差向量，同理可得K(x,X)和K(x,x)。

而f(x)的后验同样服从高斯分布：

f(x|y,X)～N(m(x),cov(x))

(7)

其预测的均值和协方差分别为:

m(x)=K(x,X)βy

(8)

cov(x)=K(x,x)-K(x,X)βK(X,x)

(9)

(10)

GP的核函数有很多种选择，如线性核函数、多项式核函数、二次有理核函数等。前文提到的噪声的标准差和核函数中的超参数一起被称为GP的超参数，记为θ。要更新模型的超参数，可采用Rasmussen等[6]的方法，先对函数f进行边缘化得到边缘似然函数:

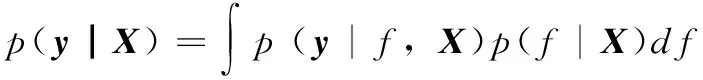
(11)

进而对边缘似然函数求对数，得到以下的对数似然函数:

log(p(y|X,θ))=

(12)

然后将对数似然函数依次对各个超参数求偏导数，就可以得到最佳的超参数数值。由以上可以看出，在预测和更新阶段都需要对协方差矩阵求逆，即计算β，这是GP计算量大的主要原因之一。

2 高斯过程回归的近似方法

根据是否把数据划分为子集，GPR的近似方法可以被分为全局近似方法和局部近似方法。局部近似方法通过一定的标准将训练数据划分为众多的子数据集，在每个子集上独立地训练一个局部GP模型，而全局近似方法则不这样。下面参考Liu等[8]给GP近似方法的分类(如图1所示)，详细介绍这两种类别。

图1 高斯过程回归的近似方法

2.1 全局高斯过程近似

全局近似旨在实现完整协方差矩阵的稀疏性，以减少协方差矩阵求逆的计算量。其中，侧重于选择训练数据的代表性子集的稀疏近似占主要地位[9]。而在稀疏近似中，先验近似方法又占大多数，其可以被分类为确定性训练条件 (DTC) 近似法，部分独立训练条件 (PITC) 近似法，回归子集 (SoR)法等。

确定性训练条件 (DTC) 近似旨在从训练数据集中选择一个活动子集(active subset)，该方法的关键是如何使选出的子集具有代表性。例如，Csató等[10]借助再现核希尔伯特空间中的投影技术，使用某个区域中数据点的平均值来代替该区域中的所有点。与上述方法中处理训练数据的随机顺序不同，Seeger等[11]利用快速前向选择策略，通过完全贪婪搜索将训练点插入活动子集中，此方法被证明与随机选择一样快速。Schreiter等[9]提出了另一种方法，以训练数据和模型之间的最大误差作为训练点连续插入和删除的标准，该方法也达到了与随机选择方案相同的速度。虽然可以获得恒定的预测复杂度，但 DTC 近似的更新复杂度随着训练点的增加而线性增长。

与 DTC 近似相反，完全独立训练条件 (FITC) 近似利用虚拟训练点的子集来实现GPR计算的加速[9]，这些虚拟训练点由训练数据经过处理得到。其在另一文献中[12]被称为伪输入，该文献的方法同时优化GP的超参数和伪输入的选取。此外，当不假设完全独立的训练条件时，可以推导出另一种方法，即部分独立训练条件 (PITC) 近似，它其实是 FITC 近似的推广[13]。

除此之外的一种近似方法是回归子集 (SoR)法，也称为确定性诱导条件 (DIC) 近似法，其在在线学习的应用中表现出了良好的性能[14]。基于减少自由变量数量的思想，Smola等[15]提出的稀疏贪婪GPR利用回归子集法，通过反复地把能使后验概率增加最大的附加函数添加到基函数集，来实现较低的计算成本。当GP核函数的 Gram 矩阵是常见的稀疏矩阵时，可以使用 Givens 旋转来更新Gram矩阵的 Cholesky 因子来降低计算复杂度，而不是重新计算 Cholesky 因子[16]。另外还有基于Bochner 定理的稀疏谱GP，例如，Lázaro-Gredilla等[17]在研究中引入了一个静态三角贝叶斯模型，旨在稀疏化 GP 的谱表示，通过线性地组合三角函数，可以近似任何平稳的GP； Gijsberts 等[18]通过用有限维的随机特征映射来近似核函数，实现了更新过程恒定的计算复杂度。尽管稀疏谱GP继承了GPR的许多理论特性[19]，但它面临预测值方差较大的问题[8]。比较 DTC 和 SoR，二者预测值的分布之间的唯一区别是 DTC预测值的方差通常更高[20]。

以上提到的方法都是先验近似方法。此外，全局近似方法还包括后验近似方法和结构化稀疏近似方法。后验近似的目标是最小化变分GP 分布和真实后验 GP 分布之间的差异。与 Csató等[10]的方法不同，Titsias[21]提供了一个变分框架，通过最大化变分下界来联合优化诱导点和超参数，该方法被称为变异自由能。同样是利用诱导点，Hensman等[22]使用随机变分推理实现了 GP 在大型数据集上的可用性。Lázaro等[23]提出了一个通用的推理框架来改进选择的诱导点，称为域间GP。

近年来，结构化稀疏近似方法也经常被研究。例如，Shen等[24]提出了一种使用快速矩阵-向量乘法策略的稀疏化方法，将训练点聚类成树状结构，这与Morariu 等[25]的方法类似。Wilson等[26]使用基于插值的核函数，为诱导点方法提供了一个一般性框架，并实现了良好的预测精度。

2.2 局部高斯过程近似方法

尽管对局部近似方法的研究不如全局近似方法多，但它们在实际应用中常常出现，因为其可以有效地降低计算成本。局部 GP 近似采用分治法(divide-and-conquer)，将训练数据分配到多个子集，在这些子集上训练局部 GP 模型。为了对训练数据进行划分和存储，经常会使用树结构来实现局部模型的构建[14,24,27]。例如，Ng等[27]使用k-d树将数据点添加到局部 GP 模型中，并在数据点达到一定数量时将现有模型划分为多个子模型。

下面以二叉树为例，介绍一种构造局部模型的方法[14]。我们考虑在线学习任务，这种情况下数据点是依次产生并被添加到GPR的。如图2所示，图中每个节点代表一个局部GP模型，其中包含一些训练样本。在学习过程刚开始时只有一个GP模型，称为根模型。随着数据点一个接一个地加入，根模型中的数据不断积累。在达到一个事先设定好的数据量阈值时，根模型被分成模型1和模型2。具体来说，根模型中所有的数据会根据一定的标准被分给这两个子模型，而分裂后的根模型中不再包含数据，该GP模型也就不存在了。随后抵达的数据点会依照同一标准继续被分配给模型1和模型2。当这两个模型中的数据量到达上限时，它们也会分裂成新的子模型，从而形成树状结构的第三层。如此重复模型的分裂步骤，局部GP模型就被构造出来了。

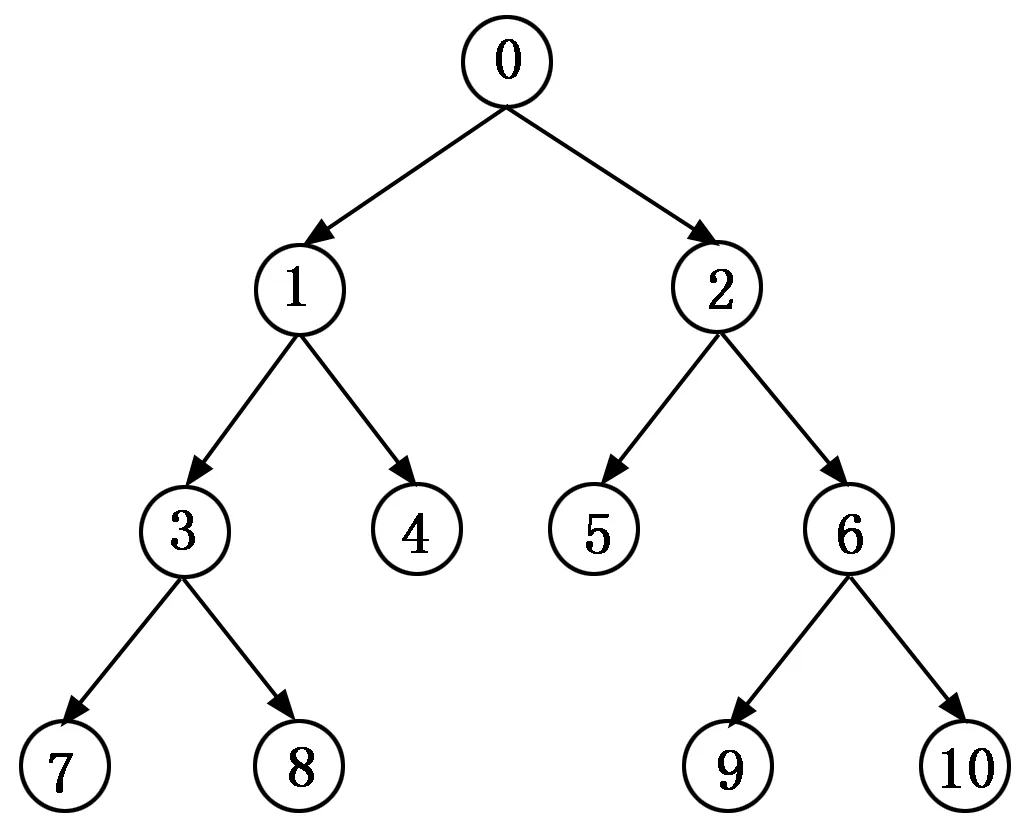
图2 树状结构的局部高斯过程模型

需要注意的是，并不是所有的局部模型都有子模型。例如图中第三层的4个模型中，模型3和模型6在下一层会分裂出新的模型，而另外两个模型则没有子模型。由于数据分配标准的原因，模型4和模型5中没有被分配到足够的数据点，故而不会到达阈值。在局部模型分裂时，数据分配标准的选择有很多种。例如对于二叉树，可以选择父模型中数据的输入集X的平均值或中位数作为边界，也可以选取最大的xi和最小的xi的平均值，然后将xi小于平均值或中位数的数据点分到左边的子模型，其他的数据点则进入右边的子模型。

在模型的预测阶段，每个局部模型都会产生一个自己的预测结果。为了将局部模型的预测结果聚合成一个全局的预测，需要一定的聚合方法。目前已经被较深入地研究的是专家混合 (mixture of experts)方法和专家乘积 (product of experts)方法。

Jacobs等[28]提出的专家混合方法已在局部 GPR近似中被广泛使用。此方法最先由Tresp[29]引入到GPR中，他们通过使用一定数量的具有单独尺度参数的M个局部GP模型，实现了将输入数据分配给相应的局部模型的功能。而Rasmussen等[30]通过基于Dirichlet过程的门控网络将训练数据划分为局部模型。这些研究都使用专家混合方法来结合多个局部模型的预测。

专家混合方法为局部模型赋予不同的权重，然后将它们加在一起以实现全局预测，而专家乘积方法则将各个局部模型的预测相乘。广义专家乘积(generalized product of experts)[31]方法使用动态权重的策略，会根据预测的不确定性相应地调整局部模型的权重。贝叶斯决策 (bayesian committee machine)[32]也是专家乘积方法的一种，它根据后验方差决定局部模型的重要性。受到从专家乘积方法到广义专家乘积方法的改进的启发，Deisenroth 等[33]提出的鲁棒贝叶斯决策(robust Bayesian committee machine)也是通过调整局部模型的权重从贝叶斯决策[32]发展而来的。

同时，也存在少量不需要聚合多个局部GP模型结果的局部近似方法。例如，Meier等[34]利用滑动窗口策略来保留一定数量的近期观测数据用于预测和更新，同时丢弃旧的数据。由于被设计用于在线学习的控制任务，训练数据沿系统状态轨迹分布，因此对于系统状态不重复的情况，旧的数据几乎与当前的控制无关，故而可以被遗忘。

虽然通过局部模型使得协方差矩阵的规模大大缩小，避免了单个模型过大带来的计算成本过高的问题，但是很多局部近似方法在进行预测时，会让所有的局部模型都参与预测，这样它们预测的计算量仍然较大。但实际上，并不是所有局部模型都与当前的预测密切相关。这点在Lederer等[14]提出的LoG-GP(locally growing random tree of GPs)中得到了改进。LoG-GP中定义了活跃模型的概念，对于一个问询点，它对应的活跃模型就是它在模型更新时可能被分配到的那些局部模型。在预测时只让这些活跃模型参与计算，而忽略其他不重要的模型，由此，预测的计算量就得到了进一步的减小。

3 高斯过程回归的应用

GPR的发展可以追溯到20世纪40年代发展起来的Kolmogorov-Wiener 理论，它为时间序列的分析提供了数学基础[35]。随后在地质分析领域，GPR的应用得到了很大的推广，被称为克里金法(Kriging)，由南非矿业工程师D.G.Krige于1952年首次提出。基于Krige等人的研究，法国学者G.Matheron提出了区域化变量的概念，于1962年正式创立了地质统计学这个新学科[36]。而后，克里金法得到了不断的拓展，发展出了简单克里金、普通克里金、协同克里金、指示克里金等分支[37]。 而GPR作为机器学习的一个分支的正式确立是在1996年由Rasmussen等[38-39]完成的[40]。

时间序列即事物随时间变化的情况，对时间序列的分析预测是GPR建模能力的直接体现。在时序预测中经常需要进行多步预测，实现多步预测的方法有递推法和直接法[41-42]。递推法使用单一的GP模型，通过多次的单步预测来实现多步预测，上一步的预测输出作为下一步的输入之一。递推法简单直观但预测误差会累积，是最常用的多步预测方法。而直接法对每个预测步骤使用一个不同的模型，并且所有模型的输入是相同的，这种方法没有累计误差但计算量较大。

在近年来的研究中， Brahim-Belhouari等[43]的研究展示了基于GP模型对时间序列的预测优于RBF神经网络。Hachino等[44]采用多重GP模型进行时间序列预测，并用可分最小二乘法训练这些GP模型。Tobar等[45]用具有非参数核函数的GPR来预测平稳的时间序列。

作为国内较早将GPR应用于时间序列分析的探索，沈赟[46]指出平稳的GP核函数适用于平稳时间序列的预测，而对非平稳时间序列则需要非平稳的核函数以达到更好的效果。李军等[47]结合平稳和非平稳的GP核函数形成复合的核函数，其对单步和多步时间序列的预测比常规GP模型更加准确，相比于支持向量机也展现出了一定的优势。

以下对GPR在一些具体的工程领域的应用进行了介绍。

3.1 用于控制领域

GPR由于其出色的非线性系统建模能力，在控制领域受到的关注不断增加。

模型预测控制(MPC)是实际应用中最常见的控制算法之一。MPC的关键是建立合适的预测模型，建模可以通过神经网络、支持向量机、模糊模型等来实现。RBF神经网络作为MPC中广泛使用的建模方法，在应用中面临着一些限制，如参数较多，网络表现受到初始连接权值和阈值选取的影响等。而GPR的参数少，训练过程相对容易。作为该领域的早期探索之一，Kocijan[48]等将GPR用于MPC得到了具有更高鲁棒性的控制器。Hewing等[49]提出了一个结合标称系统和建模为GP的动力学的混合结构，该GP部分用来学习动力学效应，所得到的MPC方法可以在很小的采样间隔下实现对系统的控制。Cao等[50]使用GP建模四旋翼飞行器的平移和旋转子系统，提出了一种飞行器的模型预测控制轨迹跟踪方案。

自适应控制是一种可以适应系统参数变化的控制方法。模型参考自适应控制(MRAC)是自适应控制的方案之一，其原理是让系统的动态特性逼近一个预先设定的参考模型。Chowdhary等[51]通过在GP核函数中加入时变变量，实现了用GP对不确定性进行概率建模，提升了自适应控制的性能。该作者的另一项研究对比了基于GP的模型参考自适应控制(GP-MRAC)和基于径向基函数网络的模型参考自适应控制(RBFN-MRAC)，指出前者具有更好的跟踪性能[52]。Joshi等[53]用生成网络架构来学习高斯模型，避免了传统的GP-MRAC中对状态导数的估计，而且该方法能保证跟踪误差的统一界限，也保持了系统的稳态性能。

此外，在具体的运动控制方面，Ko等[54]结合GPR和无迹卡尔曼滤波器(UKF)，用GPR学习运动和观测模型，同时用UKF作为状态估计器，其与单纯的UKF相比具有更好的估计效果和更广的应用范围。Marco等[55]将线性最优控制与GP相结合，提出了一种LQR控制器的整定方案，并用于机器人手臂的控制。Mukadam等[56]提出了一种高斯过程运动规划器(GPMP)，首次将GP用于运动规划。该方法用线性时变随机微分方程来表示连续的轨迹，利用 GP 插值来开发运动规划器，能确定最优轨迹，并被用于七自由度机械臂的轨迹优化中。同时，GP还被用于运动路径的预测[57]、即时定位与地图构建(SLAM)[58]等。

GPR作为一种概率性的非参数建模方法，在提供预测结果的同时还能度量预测的不确定性，这是很多其他建模方法所不具备的。因为这个优势，GP可以被用于对精度要求较严格的控制任务，这通常依赖于误差的一致有界(uniform error bound)。误差的一致有界性需要一些较严格的前提假设才能被推导出来，而这些前提条件很多时候难以全部被满足，因此在应用中实现起来并不容易。所以，还需要进一步的研究以达到更宽松的前提条件。

3.2 用于软测量

在对产品质量要求日益严格的当代社会，如何准确测量相关的质量指标是一个至关重要的问题。然而由于技术的限制，过程控制中存在很多难以直接测量的变量，如反应器中反应物的浓度[59]。于是，一种通过间接方法来推断这些不可测变量的手段被发展出来，称为软测量或虚拟测量，被广泛用于化工过程和工业制造。实现软测量的关键是选取出与目标变量相关的一组可测变量，以及如何由这些可测变量通过数学关系推导出待测的目标变量[60]。

此外，由于单一模型的测量精度有限，集成学习也被应用到软测量领域中。Wang等[61]提出了一种基于分层集成GPR模型的软测量建模方法，包括基于样本划分的集成和基于变量划分的集成。在第一层中，根据输入变量划分子数据集，再在每个子数据集中用高斯混合模型(GMM)建立多个局部GP模型；第二层将表现好的多个局部集成GPR模型的预测通过贝叶斯推理得到最终的预测值。赵帅等[62]在2019年提出了具有类似结构的软测量方法。

在实际应用中，刘国海等[63]提出了一种动态软测量方法，结合多准则策略和GPR，实现了比静态软测量更高的精度，并将其应用于生物发酵过程；孙茂伟等[64]将基于改进Bagging算法的软测量用于工业双酚A生产中的指标预测；Yang等[65]将GPR用于橡胶混合过程的质量指标的获取；R.Grbic等[66]将其用于化工领域典型的TE(tennessee eastman)过程。此外，GPR还被用来综合其他技术以实现软测量，如与近邻传播[67]、支持向量机[68]、贝叶斯决策[69]、模糊C均值聚类[70]等相结合。

测量的不确定度是除测量数值之外衡量测量精度的另一重要参数。直接测量的不确定度较容易估计，但对于软测量来说，通过误差传递等方法来估计不确定度相当困难[59]。与控制领域类似，GP在软测量中的应用也有着能够量化测量不确定度的优点。不过在目前的软测量研究中，该优点还没有被深入地挖掘。

3.3 用于其他领域

1)用于土木工程领域，如滑坡位移[71]，基坑位移[72]和水利工程中的边坡位移[73]；

2)用于气象领域，如短期风速的预测[41]，大气温湿度的预测[76]；

3)用于图像处理，如图像分割中的异常检测[77]，图像中的运动目标检测[78]；

4)用于电力系统，如电力需求的预测[79]，变压器的故障诊断[80]，等等。

总的来说，由于其出色的非线性建模能力，参数较少，并能给出预测的方差，GPR在实际应用中展现了其优越性。如果能在降低其计算复杂度的基础上进一步发挥这些优势，其应用范围将会得到持续的拓展。

4 结束语

GPR是一种强大的机器学习建模方法。为了克服其计算量随训练数据大幅增加的问题，各种各样的近似方法被开发出来，包括整体近似和局部近似。GPR已经在众多领域得到了应用，为了使其变得更加完善，以下方面还有待有进一步的研究：

1)虽然GPR能够保证回归误差的有界性(以一定概率)，但是一些近似方法并没有继承这个性质，因而在对预测准确性要求很高的任务中无法被采用，如精密制造任务或与人相关的机器控制任务。但也有很多GP近似方法在近似后还保留了误差有界性的优点。

2)全局近似方法的策略是选取一部分有代表性的数据，而其他冗余的训练数据可以被丢弃，这使得它们对存储空间的要求不高；而由于降低计算复杂度的原理不同，大多数局部GP近似方法会保留所有数据。这使得它们在应用中还会面临设备存储容量不足的问题，特别是对一些内存较小的设备，如无人机等。随着数据采集技术的发展和传感器成本的普遍降低，各种场景中产生数据量不断增长，此问题如果得不到有效的缓解就会限制局部近似方法的应用。

3)当今，越来越多的应用场景需要实现在线建模，即通过在线收集的数据完成实时建模。相比于离线建模，在线建模对数据的利用率要高得多，并且能实现模型的动态调整。然而，在线建模需要面对更多的挑战，对计算速度的要求也更高，实现难度更大。例如，很多局部GP近似方法需要在提前已知训练数据的情况下才能完成局部模型的构建，故而类似图2中展示的通过实时数据生成局部模型的方法就不适用了，它们也无法用于在线建模任务。在利用GPR完成实时建模的方面已经有一些研究，但还需要更深入的探索。