基于FA-SVR 的气膜混凝土成本预测研究

项崇涛XIANG Chong-tao

（中交第三公路工程局有限公司，武汉430035）

0 引言

绿色施工是指在保证建筑质量和安全目标的前提下，运用科学的管理和技术手段，尽可能节约资源，提高施工过程的环境友好性，遵循促进建筑的可持续利用理念的施工过程。气膜混凝土（reinforced concrete structures using inflated forms，RCSUIF）因具有对施工环境微影响、工期紧凑、环境友好等优点，更符合绿色施工理念要求，已经成为学者们研究的热点，但研究主要集中在其力学和材料优越性能方面，而关于RCSUIF 成本控制的研究较少。在施工过程管理中，采用定性与定量分析的方法对项目成本进行准确的判断和推测，以期成本可控是确保施工顺利进行的重要保证。因此，在施工前期对施工成本进行有效的预测，不仅可以有效的控制施工成本，而且还能有针对性地找出施工过程的薄弱环节，进而提高施工管理整体水平。

萤火虫算法（Firefly Algorithm，FA）作为基于仿生学的群体智能优化算法领域的最新成果之一，FA 在寻找全局最优解方面相对于遗传算法（Genetic Algorithm，GA）和粒子群算法（Particle Swarm Optimization，PSO）等仿生算法效率更高，更不易陷入局部最优。

本文提出将萤火虫算法（FA）和支持向量回归算法（SVR）结合，建立基于FA 改进的SVR 模型进行气膜混凝土主体工程成本预测综合评价，并进行模型对比研究。

1 FA-SVR 模型原理

1.1 FA 算法

Yang（2008）提出了一种基于萤火虫群体行为模拟的仿真优化算法，即萤火虫算法（Firefly Algorithm，FA）。萤火虫仿真优化算法中，自然界的萤火虫个体由搜索空间中的点进行仿真模拟，进而将自然界的萤火虫之间的光度吸引和位移用程序的搜索和优化过程进行模拟，并且把最优解求解的目标函数量化为萤火虫在空间的位置优劣，进而把萤火虫位置进化过程模拟为最优解的求解与迭代过程。根据萤火虫算法中的吸引度和亮度两个参数的不断迭代，实现目标函数的最优解的优化求解过程。优化求解如下：

首先定义萤火虫的相对亮度为：

公式（1）中，I0、γ、rij分别表示萤火虫的最大亮度、光强度的吸收系数以及i 与j 在空间的距离。

其次定义萤火虫的吸引度为：

公式（2）中，β0表示光源r=0 处的吸引度，亦即最大吸引度。其中光强度吸收系数为常数γ。

并且，萤火虫i 由于被吸引而向j 移动的位置变换如下：

公式（3）中，x，xj分别代表萤火虫i 和萤火虫j 的空间位置；步长因子用α 表示，α 作为[0,1]间的常数；rand 表示[0，1]之间的均匀分布的随机因子。

1.2 SVR 模型

支持向量机（Support Vector Machine，SVM）理论起源于小样本数据处理大发展的20 世纪后期。SVM 的建模过程要求将样本数据设置为训练集和测试集，其中将训练集作为输入向量进行训练计算，构造出最优的决策函数模型，进行预测分析。而SVR 则是SVM 的一个拓展用于回归拟合，发展成为支持向量回归算法（Support Vector Regression，SVR）。SVR 核心思想是通过非线性变换φ（x），使得原来在低维空间存在非线性关系的数据样本转变为具有高维特征空间特征。进一步构建线性决策函数，其回归函数可用公式（4）表示：

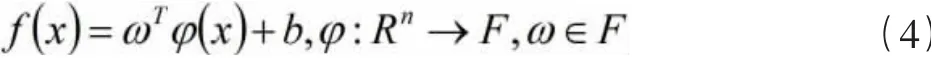
同时，引进下述结构风险函数：

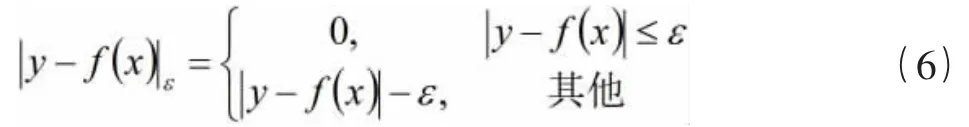
上述公式表示的回归问题，其最小化代价泛函数表示为：

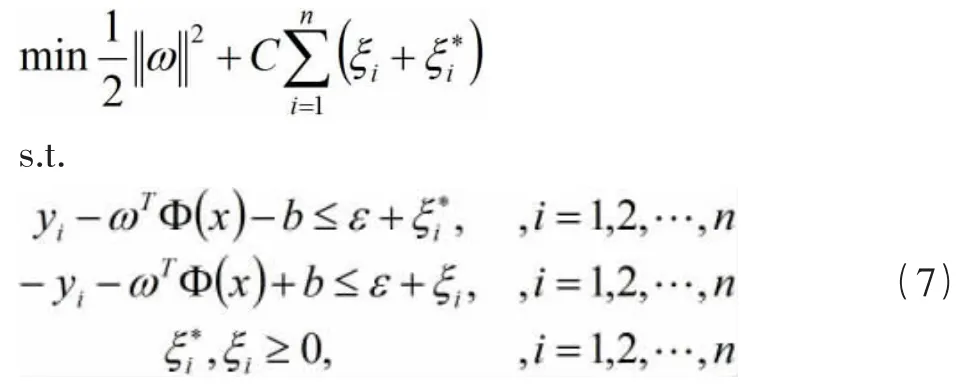
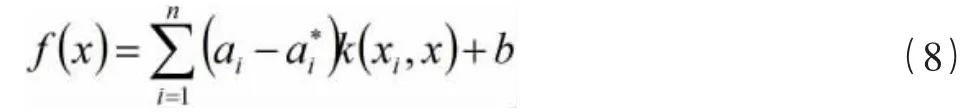
在公式（9）中，将测试集的输入向量、训练集的输入向量和阈值分别设为x、xi和b。

1.3 FA-SVR 模型优化原理

构建基于FA-SVR 的气膜混凝土施工成本预测需要如下步骤：步骤一：建立预测模型指标体系，确定SVR 回归模型所需的训练样本与预测样本；步骤二：采用FA 算法进行SVR 模型参数寻优；具体寻优过程如图1 所示：其中，Step1 的基本参数设置时，将萤火虫数目个体数、光吸收系数、Max 吸引度、步长分别设定为m、γ、β0、α；Step2，初始化萤火虫位置，进而将计算得出的萤火虫各自目标函数值当做其本身最大荧光亮度；Step3，根据公式（1）和公式（2），运算萤火虫各自的相对亮度和吸引度；再根据相对亮度的大小判断萤火虫的位移。Step4，根据公式（3）计算萤火虫的当前空间位置，然后对最优空间位置的萤火虫个体施以扰动，进而根据扰动后的位置，再一次计算萤火虫在当前位置的亮度。Step5，若搜索精度满足了设定要求，或者在达到最大搜索次数时输出全局极值点和最优个体；否则，搜索次数加1，继续转步骤三，进行下一次搜索。Step6，输出全局极值点和最优个体。步骤三：利用FA 算法寻优的最优数据结合1.2 中SVR 模型得到的回归函数（公式（9））所示对测试样本进行预测评价。

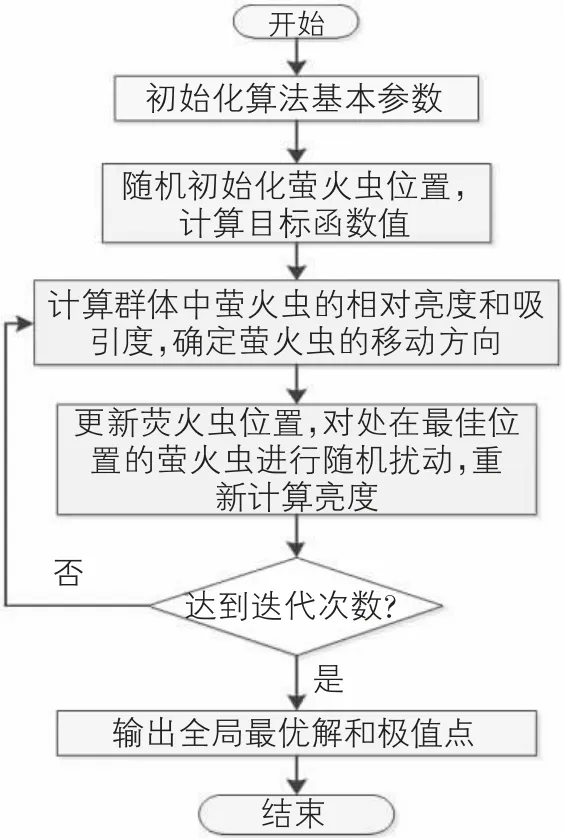
图1 FA 优化示意图

2 实例分析

2.1 建立指标体系

本文结合已有文献，根据气膜混凝土主体结构自身的特点，从安全水平、管理水平、质量水平和现场施工条件为定性指标；工期、设备使用率及物价水平为定量指标，建立RCSUIF 施工成本预测指标体系如图2 所示。

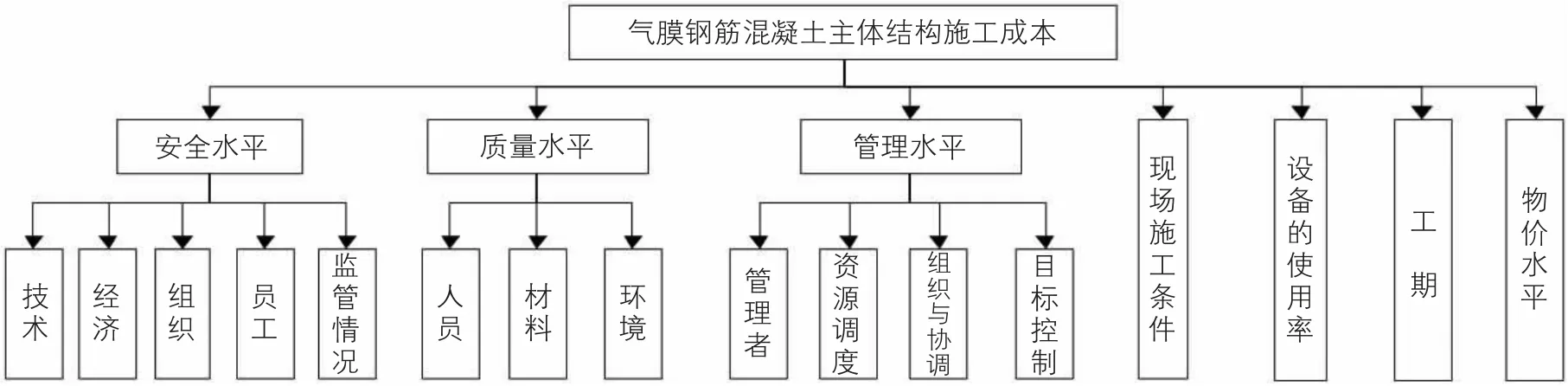
图2 RCSUIF 施工成本预测指标体系

部分指标体系简要说明：①安全水平。安全是指标体系中首要指标，是项目施工首要目标，包括技术安全、经济安全、组织安全、员工安全和监管的安全五部分。②质量水平。质量作为气膜混凝土项目管理的三大目标之一，质量水平的好坏主要取决于施工人员和施工所需的材料以及施工的环境，有较高的质量水平，则是施工成本和施工进度保证的前提。③管理水平。项目施工成本控制需要高效的管理团队，管理者的管理水平直接影响项目施工的组织过程以及资源的调度问题。④现场施工条件。气膜混凝土项目管理现场施工条件，包括当地气候、水文地质、自然环境、人文文化、社会氛围等诸多因素。现场施工条件往往也是影响现场施工的重要条件之一。

2.2 量化指标

这一步是将原始数据，经过一定的量化处理使其规范化。其中安全水平、质量水平、管理水平之类的定性指标运用层次分析法（Analytic Hierarchy Process，AHP）来确定指标权重，进而采用德尔菲法确定评价指标，最终应用综合指数计算评价值；而现场施工条件指标，结合项目所在当地气候、水文地质、自然环境、人文文化、社会氛围等条件，利用主观赋值法进行打分，再参与综合运算。

定量指标使用具体的原始数据，量化方法如下：设备使用率，通过现场的统计确定；工期（天），按实际工期取值。而物价水平，则以2009 年当地物价为基数，采用PPI逐月加权平均进行确定。

2.3 原始数据收集

本文以ZM 建筑安装工程集团有限公司建设完成的21 个气膜钢筋混凝土结构主体工程为研究目标，进行数据收集集，如表1 所示。

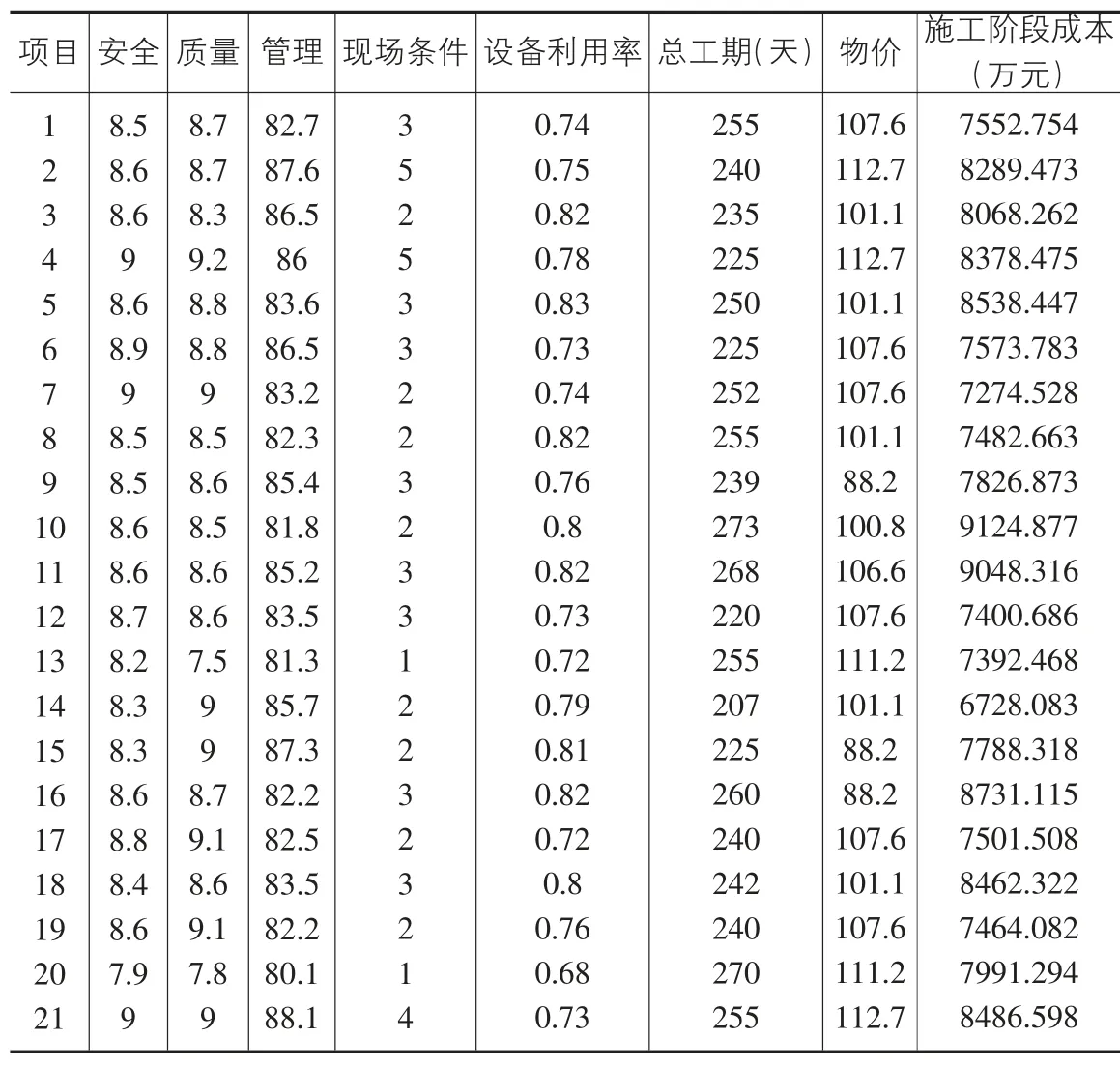
表1 气膜混凝土的施工原数据

2.4 指标数据的处理

为了研究方便消除量纲的不统一，本文采用归一化函数如公式（10），将矩阵的每一行处理成[0，1]区间的指标数据进行施工成本预测如表2 所示。即通过：

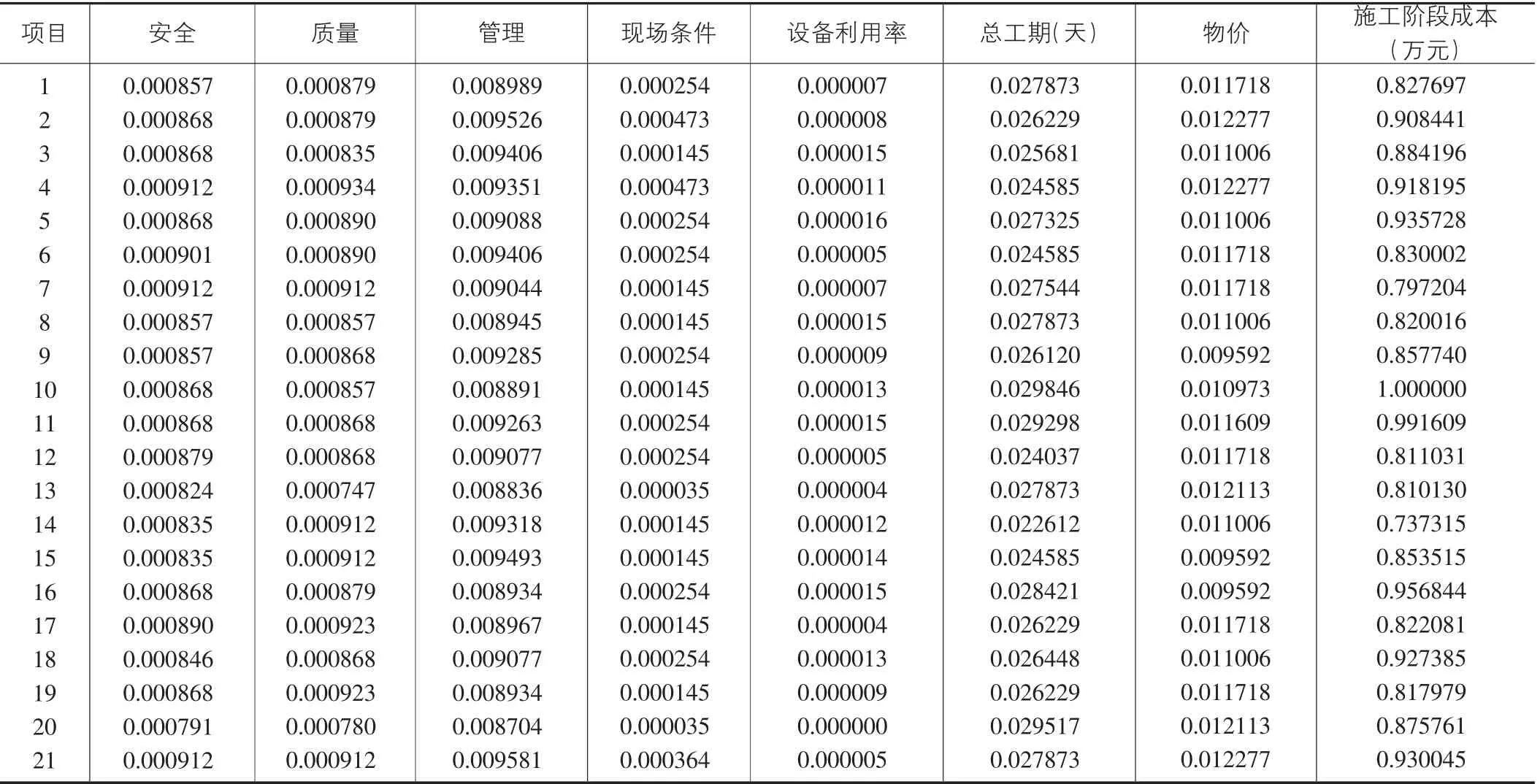
表2 归一化数据

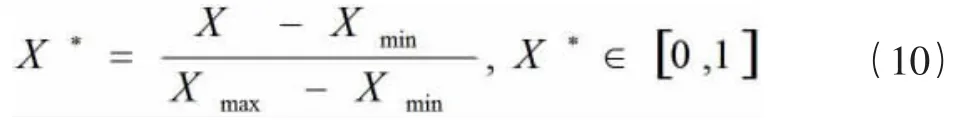
公式（10）中X*，X，Xmax，Xmin分别为归一化数据、原数据、原数据中的最大值和原数据中的最小值。

2.5 对比分析过程

利用2.4 处理后的样本数据，在MATLAB2016a 平台上按照1.3 步骤进行寻优实现对样本的预测。在具体操作中，将归一化后的前16 组数据，作为预测模型的训练集；而将归一化后的后5 组数据，作为预测模型的测试集。运用MATLAB2016a 进行运算和结果输出，体现该模型的拟合能力和预测能力。

先后运行FA-SVR 模型和PSO-SVR 模型，设置粒子的速度更新参数C1=1.5，C2=1.7。具体输出情况如图3-图6所示。

针对FA-SVR 预测模型优越性的验证，本研究采用引入PSO-SVR 预测模型，对其施工成本进行从预测值、相对误差、训练集误差（trainMSE）和测试集误差（testMSE）等方面进行对比分析，具体结果如表3 所示。

2.6 结果分析

①从图3 和图4 可以看出FA-SVR 模型比PSO-SVR模型的平均适应度波动小，并且由图3 和图4 可知在优化过程中FA 模型的最佳适应度曲线首先达到最佳适应值，同时FA-SVR 模型的best c=3.511、g=0.011542，PSO-SVR模型的best c=4、g=0.084496，前者的best c 和个都明显小于后者，说明了FA-SVR 模型的先进性。

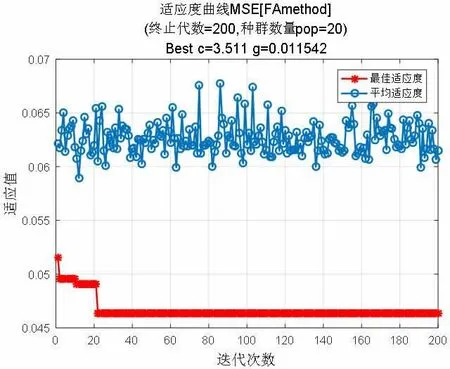
图3 FA-SVR 模型适应度曲线图

图4 PSO-SVR 模型适应度曲线图

②从图5 和图6 可以看出FA-SVR 模型训练集数据较PSO-SVR 模型更好的接近于真实数据，预测更准确。

图5 两模型训练集预测曲线对比图

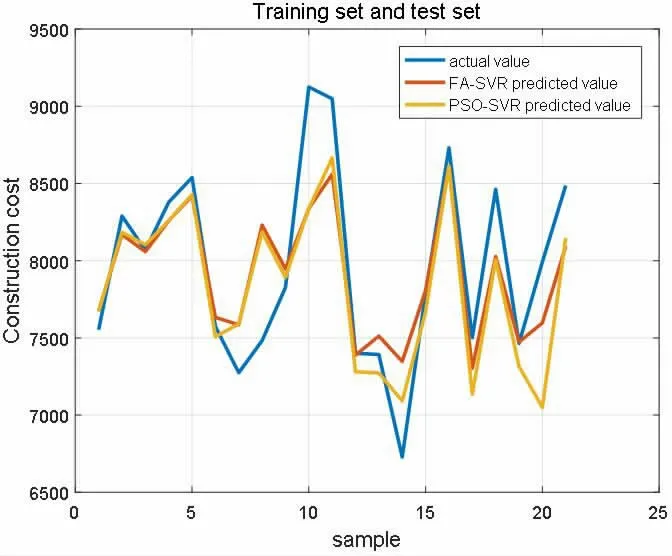
图6 两模型预测结果对比图

③从表3 工程编号为17、18、19、20 中得出FA-SVR模型相对于PSO-SVR 模型，其预测结果相对误差更小，准确率更高，而样本21 则两个模型相差不大，同时从表中可知FA-SVR 模 型 的trainMSE=0.0414、testMSE=0.0691，PSO-SVR 模型的trainMSE=0.1481、testMSE=0.2000，前者的trainMSE 和testMSE 都明显小于后者，说明FA-SVR 模型的预测能力强于PSO-SVR 模型。

表3 不同模型的预测结果

3 结论

本文针对施工成本预测问题，在构建气膜混凝土施工成本的预测指标体系基础上，引入FA 优化算法，构建了基于FA-SVR 的气膜混凝土施工成本的预测模型。并在国内已有的21 个工程样本基础上与PSO-SVR 模型进行了对比验证研究，验证显示，FA-SVR 模型整体在寻优方面更优于PSO-SVR 模型。同时FA-SVR 模型训练集数比PSO-SVR 模型更接近于真实数据，且平均适应度波动更小，收敛效果更好，预测结果相对误差更小。由此可见FA-SVR 模型的预测能力强于PSO-SVR 模型，预测精度更准确，为气膜混凝土结构工程成本预测提供了一种新的预测模型。