基于滑模逆解耦的小型永磁直驱风力发电系统最大风能捕获方法
王鸿儒,张志刚
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
0 引言
目前,MW级别大型风力发电机产业处于快速扩张阶段,小型风力发电机产业由于拥有功率小、惯性小、设计成本低以及对建设场地要求低等特点,同样也在不断发展中[1]。特别是变速风力发电系统,相比传统的定速风力发电系统,其不仅降低了机械负荷,而且在增加能量捕获方面颇具优势[2-3]。
从变速风力发电系统提取最大风能的控制策略主要分为3种,分别是最佳叶尖速比控制(tip speed ratio,TSR)、最优转矩控制(optimal torque,OT)以及扰动观察法(perturbation observation,PO)[3]。TSR作为使用最广泛的风力发电最大风能捕获控制方法之一,对风速变化的反应较快[4]。然而,永磁同步发电机(permanent magnet synchronous generator,PMSG)控制系统是一个非线性强耦合系统,在传统TSR方法中,在线性控制器下不能呈现良好的动态特性[5]。
逆系统的方法被用来解决系统强耦合以及非线性的问题。其通过原始被控系统的数学模型构造其逆系统,并将两个系统级联,构成伪线性系统,使系统具有线性性质,进而运用线性系统理论对伪线性系统进行控制。文献[6]运用逆系统的方法,将原始的Boost变换器控制系统中的内电流环和外电流环进行解耦并且补偿。文献[7]将逆系统设计应用于光通信系统中,对拉曼放大器进行优化,解决了克尔非线性水平增加的问题。文献[8]将逆系统的方法运用在智能汽车控制中,对纵向速度和横摆角速度进行反馈调节,提升了智能汽车路径跟踪的精确性和行驶稳定性。文献[9]运用逆系统的方法对磁悬浮控制敏感陀螺的两个测量轴进行解耦,使其测量精度得到了提高。本文提出了一种基于逆系统的最大风能捕获控制方法,使系统拥有更好的动态性能。
传统的PMSG控制中,转子的位置通常是由机械式传感器进行采集,逆系统的模型构建也需要对电机的转矩进行采集,而使用机械式传感器无疑会增加小型风力发电系统的体积、重量以及设计成本。无传感器控制方法主要包括电机反电动势估算法、高频注入法、卡尔曼滤波器法、状态观测器法以及滑模观测器法等,这些方法都能够很好地解决上述传统PMSG控制所带来的问题[10]。电机的反电动势估算法较为简单,但是在电机低速运行时容易造成较大误差[11]。在文献[12-13]中高频注入法、卡尔曼滤波器法以及状态观测器法的鲁棒性和控制效果较好,但是在使用过程中存在大量的计算以及对参数敏感等问题。
本文选择使用结构简单且抗干扰能力强的滑模观测法(sliding mode observer,SMO)。传统的滑模观测器工作时本身会出现高频抖动;并且在电机低速度时,由于反电动势微弱难以被提取,导致估计误差较大[14]。本文采用Sigmoid函数代替传统的sign函数,期望较大程度地消除系统本身的抖动现象;在低频滤波器前引入一个放大因子ks,用于放大反电动势的信号以便于滤波器提取,并在此基础上提出了一种基于滑模逆解耦的最大风能捕获控制方法。
1 永磁直驱风力发电系统
永磁直驱风力发电系统的特点是风力机与永磁同步发电机的转子通过传动轴直接耦合,建立其数学模型有助于对控制方法的理解和改进。
1.1 风力机模型

1.2 永磁同步发电机模型


2 基于逆系统模型的控制器设计
对PMSG系统的可逆性进行分析后,将求得的逆系统模型与PMSG控制原系统(简称“原系统”)进行级联,所构成的复合系统对外呈线性特性,称之为伪线性系统。将其应用在最大风能捕获控制中,会使PMSG线性化解耦,拥有更好的动态性能。
2.1 系统模型


2.2 基于逆系统的最大风能捕获控制
将推导出的PMSG逆系统与原系统级联,即可以将原系统线性化,构造成一个伪线性系统,如图1所示。为使风能利用效率最大,需要控制叶尖速比,使之保持在最佳位置。风能利用效率达到最大时,对应的叶尖速比值被称为最佳叶尖速比λopt,该值由风力机的结构决定,一般为某个固定值。结合传统TSR的转速控制,用所构造的伪线性系统替换原系统,测量实时风速;最佳叶尖速比λopt与风轮半径取给定值,参考电流取0,利用式(4)计算参考转速。基于逆系统的最大风能捕获控制器的等效原理如图2所示。
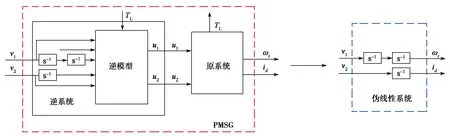
图1 基于逆系统模型的伪线性系统框图Fig.1 Pseudo-linear system block diagram based on inverse system model
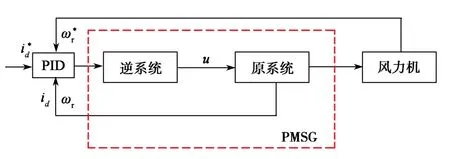
图2 基于逆系统的最大风能捕获控制器等效图Fig.2 Equivalent diagram of the maximum wind energy capture controller based on inverse system
图1和图2中,逆系统与原系统级联形成的伪线性系统可使PMSG具有线性性质。线性控制器PID能够达到良好的动态解耦效果,在风速变化的情况下,更快更稳定地控制PMSG转速,使风力机始终保持在最佳叶尖速比下运行。
3 基于改进SMO的逆系统控制器设计
在传统的PMSG控制系统中,电机转子的角度、速度以及机械转矩是通过机械式传感器而采集的,这样增加了PMSG的体积、重量以及风力发电系统的生产成本。
传统的滑模观测器将控制律设定为sign函数,频繁开关会导致系统抖振较大。为此,本文使用Sigmoid函数取代sign函数,以减小系统抖振并提高观测器精度。
3.1 改进型电流滑模观测器
根据式(5),推出PMSG在两相静止坐标系下的电流状态方程:
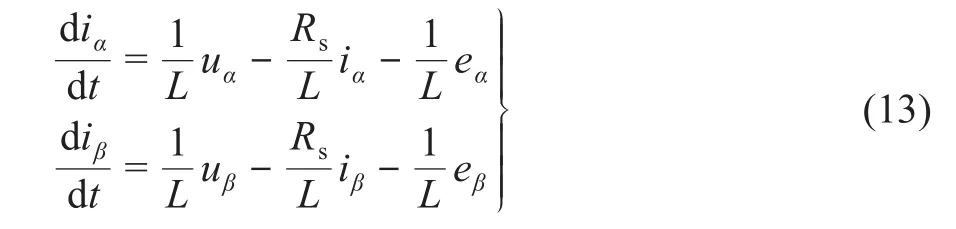
式中:iα,iβ——两相静止坐标下的定子电流;uα,uβ——两相静止坐标下的定子电压;eα,eβ——两相静止坐标下的扩展反电动势。
根据式(13)的数学模型与滑模变结构理论,定义切换函数:

选取滑模切换面:

根据式(13)的数学模型与滑模变结构理论,构造电流滑模观测器:
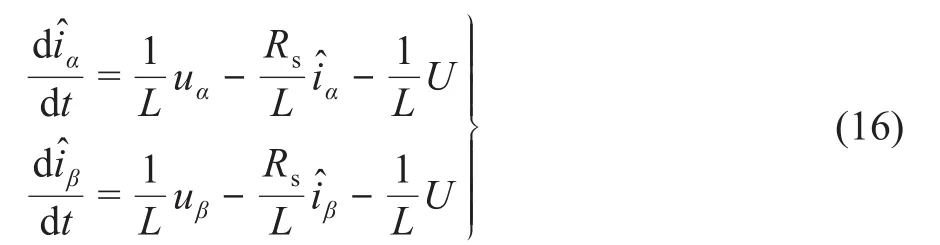
图3示出传统sign函数和Sigmoid函数的曲线图。可以看出,传统的sign函数在过零点时,直接从-1突变为1,这使得整个系统会出现高频抖动现象;而Sigmoid函数则平滑地过零点。
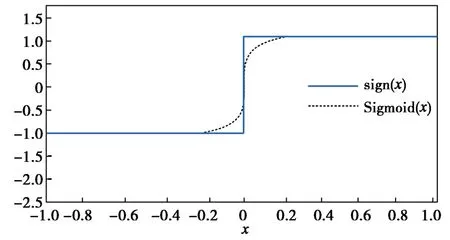
图3 sign函数和Sigmoid函数曲线图Fig.3 Graphs of sign function and Sigmoid function
因此,滑模控制律采用Sigmoid函数取代传统的sign函数:

式中:k——电流滑模增益系数,k>0,该值会直接影响系统稳定;a——可调参数,其与滑模趋近速度有关。
将式(16)与式(13)做差处理,可得定子电流的观测误差方程:
而设计的定子电流观测误差为

此时,可以得出反电动势:

在传统的SMO方法中,通常需要引入一个低通滤波器来获取连续的扩展反电动势观测值;而在电机低速运转的工况下,反电动势信号较弱,难以被提取。在低通滤波器前加入放大因子ks,可有效增大反电动势的信号,便于提取滤波器。将估算后得出的电机转子角度与速度再缩小为原来的,以保证估算值的准确性。
根据扩展反电动势可以得出电机转子的角度与速度:

PMSG系统的电流滑模观测器原理如图4所示。根据图4观测得到的电机转子角度被用于PMSG系统的坐标变换中,观测得到的电机转子速度被用于转速外环的反馈以及机械转矩滑模观测器。

图4 改进的电流滑模观测器Fig.4 Improved current sliding mode observer
3.2 改进型机械转矩滑模观测器
式(12)逆系统的模型需要转矩的值,所以有必要对TL进行观测,本文利用改进型机械转矩滑模观测器进行转矩观测。


为了保证PMSG系统的稳定性,使反馈增益g小于0。PMSG系统的机械转矩滑模观测器原理如图5所示。根据图5观测得到机械转矩,将其代入式(12)中,构建PMSG逆系统模型。
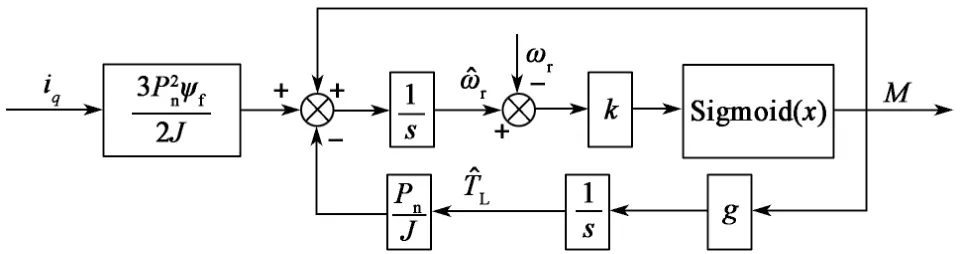
图5 改进的转矩滑模观测器Fig.5 Improved torque sliding mode observer
3.3 基于滑模逆解耦的最大风能捕获控制
结合第2节提出的基于逆系统最大风能捕获控制策略以及第3节设计的改进型滑模观测器,本文提出一种基于SMO的逆系统最大风能捕获控制方法,其原理如图6所示。该方法基于传统的TSR方法,将逆系统线性解耦方法加入PMSG的控制策略中,构建新的复合系统并具有伪线性性质,而伪线性系统在线性控制器下拥有更好的动态性能。使用改进的滑模观测器取代传统的机械式传感器,能够减小电机体积、减轻重量并降低设计成本,观测值将被用于PMSG逆系统模型的构建:电流滑模观测器所观测的电机转子的速度将被用于转速外环的反馈以及转矩滑模观测器,所观测的转子角度被用于PMSG系统的坐标变换中;转矩观测器观测的机械转矩将被用于PMSG逆系统的模型构建。
4 仿真结果与分析
仿真分为两部分:第一部分将对比滑模观测器的观测值与电机运行的实际值,用以验证所提出的改进型滑模观测器的有效性;第二部分将对所提出的基于滑模逆解耦最大风能捕获控制方法进行仿真,并对比传统方法,用以验证提出方法的有效性。结合图6所示的基于滑模逆解耦最大风能捕获控制原理,采用Matlab/Simulink软件进行仿真。控制参数经过反复试验取最优值,仿真实验用PMSG与风力机的关键参数如表1所示。
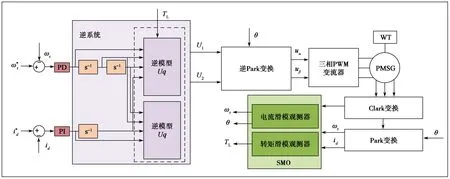
图6 基于滑模逆解耦的最大风能捕获控制原理Fig.6 Control theory of maximum wind energy capture based on sliding mode inverse decoupling
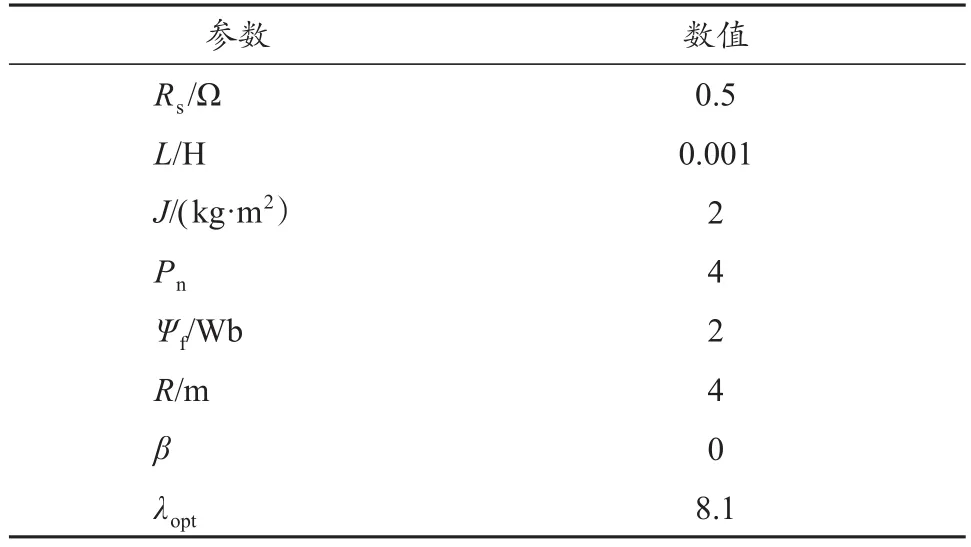
表1 PMSG与风力机的关键参数Tab.1 Key parameters of the PMSG and the wind turbine
4.1 电机参数
图7示出PMSG转子观测转速与实际参考转速对比。可以看到,由电流滑模观测器观测的PMSG转速值在启动阶段有一段超调,但马上恢复稳定;在运行阶段,能够快速且稳定地跟随实际转速参考值。图8示出PMSG观测转子位置和实际转子位置。可以看到,由电流滑模观测器观测的PMSG转子角度与实际角度的误差较小。图9示出PMSG观测转矩和实际参考转矩。可以看到,PMSG转矩观测值与参考值相比,抖动范围在0.5 N·m内,能够稳定且快速跟随参考值。
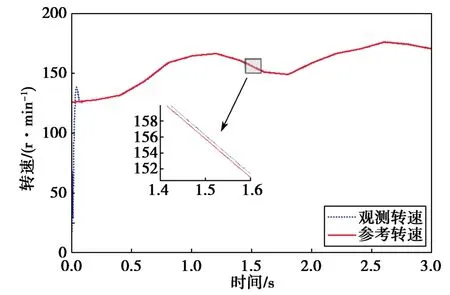
图7 PMSG转子观测转速和实际参考转速Fig.7 PMSG rotor observation speed and actual reference speed
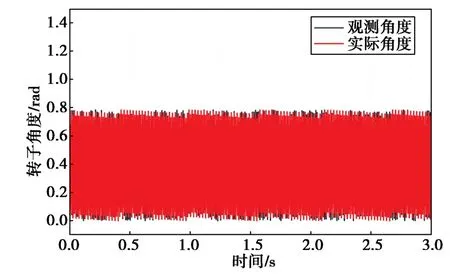
图8 PMSG转子观测角度和实际转子角度Fig.8 PMSG rotor observed position and actual rotor position
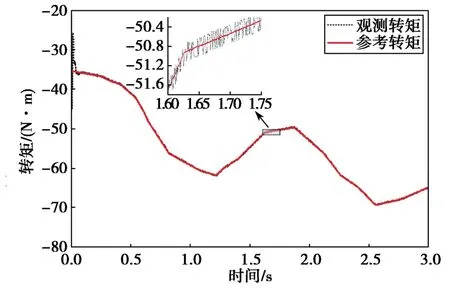
图9 PMSG观测转矩和实际参考转矩Fig.9 PMSG observation torque and actual reference torque
综上可知,所设计的滑模观测器拥有较好的动态性能,在PMSG运行时,能够稳定且精准地观测转子位置、转速以及机械转矩。
4.2 最大捕风能力
将所提出的基于滑模逆解耦最大风能捕获控制方法与传统的TSR方法作对比,模拟一段输入风速在2~8 m/s范围内变化的阵风(图10)。
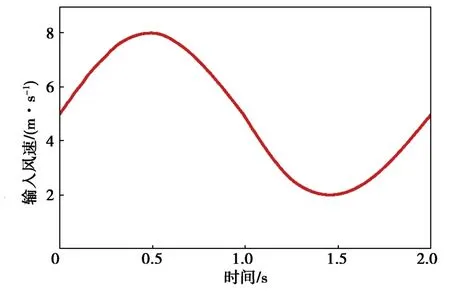
图10 输入风速Fig.10 Input wind speed
图11示出本文所提方法的转子转速与传统TSR方法的转子转速对比。可以看出,在风速变化较快时,采用本文所提方法拥有更小的超调量与更短的调节时间;在风速缓慢变化时,该方法也能更稳定地跟踪参考转速。
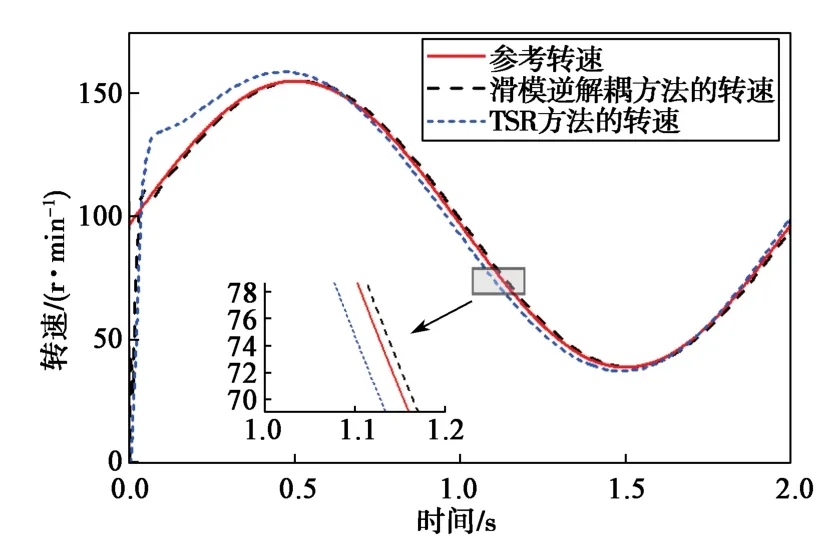
图11 基于滑模逆解耦方法的转子转速与传统TSR方法的转子转速对比Fig.11 Comparison of rotor speeds based on sliding mode inverse decoupling method and traditional TSR method
图12示出用本文所提方法的叶尖速比λ与风力机的最佳叶尖速比λopt对比。可以看出,在本文所提方法的控制下,风力机的实际叶尖速比值始终保持在最佳值附近,从而达到最大风能捕获的目的。
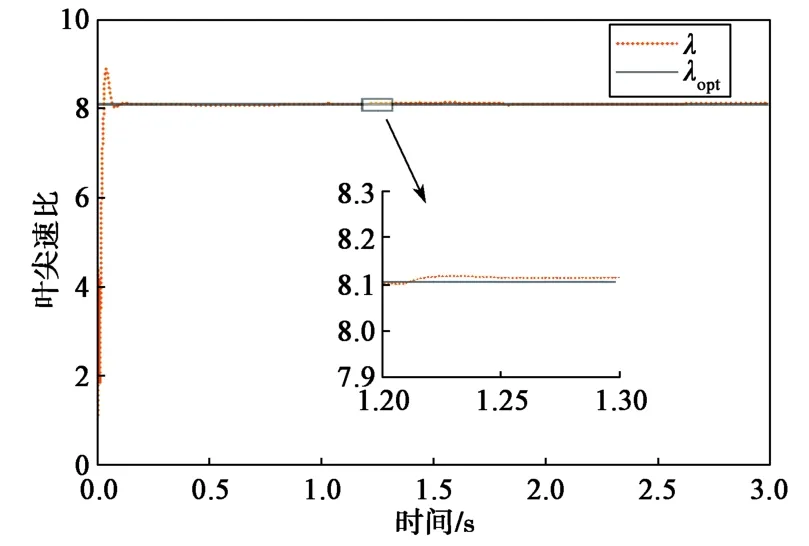
图12 基于滑模逆解耦最大风能捕获方法的叶尖速比与λopt对比Fig.12 Comparison between the blade tip speed ratio based on sliding mode inverse decoupling maximum wind energy capture method and λopt
5 结语
由于PMSG具有非线性、强耦合的特点,传统的最大风能捕获控制存在动态性能不佳的问题。对此,本文提出一种基于滑模逆解耦的最大风能捕获控制方法,其对PMSG原系统进行了线性补偿,使用逆系统的方法将原系统伪线性化,使系统在动态情况下更适用于线性控制器。在小型风力发电系统中使用改进的滑模观测器来取代传统的机械式传感器,能够很大程度地消除自身抖动,从而在全速段准确地估计转子的角度与转速,以及机械转矩。
本文所提逆系统模型的构建依赖于精确的电机参数,而在实际工程中,电机参数可能存在误差,如何规避电机参数不精确带来的问题这是下一步的研究方向。

