高阶思维视角下的几何定理教学——以“三角形一边的平行线性质定理的推论”为例

200233 上海市世界外国语中学 梁 舒

《义务教育数学课程标准》(2011年版)指出，教学活动应当培养学生运用数学的思维方式进行思考，增强发现和提出问题的能力，分析和解决问题的能力

.

按照布鲁姆的认知目标分类(此处看作思维目标)，教学目标依据认知复杂程度由低到高分为识记、理解、应用、分析、评价、创造六个层次，其中后三层(分析、评价、创造)被称为高阶思维能力

.

高阶思维体现了时代对人才素质提出的新要求，也是适应时代发展的关键能力

.

因此，在数学教学中应注重渗透数学思想和方法，培养学生的思维，尤其是分析、评价和创造层次的高阶思维

.

学生高阶思维培养的主要场所是数学课堂

.

因此，教师在设计引入、概念形成、例题处理以及小结的各个环节上如何设计思维任务，启发学生的高阶思维显得尤为重要

.

笔者以“三角形一边的平行线性质定理的推论”为例，阐述对高阶思维视角下课堂实施的见解

.

一、 教学环节

(一)情境导入

原题

一台幻灯片投影仪被安装在距离屏幕4米处，幻灯片距离投影仪16毫米(如图1所示)，

AD

∥

BC

，如果幻灯片是一张长为22毫米、宽为16毫米的图片，求图片投影在屏幕上图像的长和宽

.

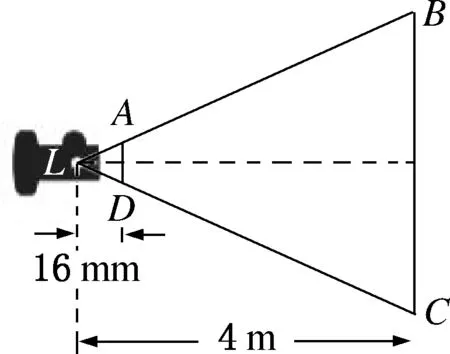
图1

师：题目中有哪些已知信息？三角形一边的平行线性质定理的条件和结论分别是什么？(引导学生对题目进行分析，尝试将其与已学知识建立联系)

生：已知

AD

∥

BC

以及一些线段的长度

.

条件是有一条平行于三角形一边的直线截其他两边所在的直线，结论是截得的对应线段成比例

.

图形语言表述如图所示，其中图2-1、图2-2为A字型图形，图2-3为X型图形.

图2-1图2-2

图2-3图3

生：题目符合A字型

.

(定理转换为图形语言后，学生很容易与A字型联系起来)

师：题目满足性质定理的条件，运用性质定理能否求得图片投影在屏幕上图像的长和宽，能否解决该问题？(引导学生将题目的所求与性质定理的结论进行对比，发现性质定理的局限)

生：不能

.

如图3，将问题抽象成A字型后，图像的长是图中

BC

的长，

BC

不在三角形被截的两边所在的直线上，性质定理的结论中没有涉及这种情况

.

学生对比后发现虽然题目中的图形符合A字型，也满足相关条件，但运用性质定理的结论却无法解决该问题，进而产生了认知冲突

.

(二)探究三角形一边的平行线性质定理推论

师：在性质定理的结论中，有关的比例线段分别在三角形两边所在的直线上，图形中线段

DE

虽不在三角形被截的两边上，但是它和图形中其他线段之间是否存在比例关系？(向学生指明思考的方向)师：先考虑

D

和

E

分别是三角形两边中点的特殊情况

.

(学生已学习中位线定理，较容易解决此问题)

图4

问题1

如图4，如果点

D

，

E

分别在△

ABC

的边

AB

，

AC

上，且

D

，

E

是边

AB

，

AC

的中点，

DE

∥

BC

，那么成立吗?师：再考虑

D

和

E

是三角形两边上任意一点的一般情况

.

(引导学生对一般情况进行分析思考，培养学生分析问题的能力)

问题2

问题1中点

D

和点

E

位置改变时，图形存在哪几种情况？根据“点的位置移动”，学生可能画出的图形如图5-1—图5-9所示

.

图5-1图5-2

图5-3图5-4

图5-5图5-6

图5-7图5-8

图5-9

师:大家画出的图形与问题1中的图形相比有什么异同？是否可以按某种标准将上述图形进行分类呢？(引导学生将情况分类，发现性质定理推论的条件)

生：按照

DE

是否与

BC

平行进行分类

.

结合图形和已学性质定理，学生能较为容易地对图形进行分类，如下所示

.

问题3

在图5-3和图5-6两种情况下，是否仍然成立?如果成立，请给出证明

.

请大家分小组讨论，之后每组选出一位同学分享

.

师：

D

，

E

分别在△

ABC

的边

AB

，

AC

上时，如图5-3的情况如何证明？

图6-1图6-2

方法1：

过

D

作

DF

∥

AC

交边

BC

于点

F

(如图6-1)

.

方法2：

延长

DE

到

G

，使

DG

=

BC

，联结

CG

(如图6-2)

.

学生在证明中位线定理时已经运用过方法2，故学生较易得出此方法

.

对于方法1，学生之前没有构造此类辅助线的经历，可能需要教师引导

.

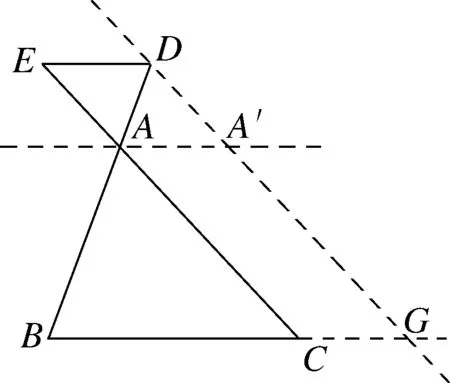
图7

师：

D

，

E

在

AB

，

AC

延长线上时，图5-6情况下的X型如何证明呢？学生在证明性质定理的时候证明过X型，故可思考得出通过构造辅助线将X型转化为A字型来解决(如图7所示)

.

师：从上面的证明中，你能得到什么结论？请一组同学分享，其他组补充

.

生：平行于三角形一边的直线截其他两边所在的直线，截得的三角形的三边与原来三角形的三边对应成比例

.

学生类比性质定理的描述，能较为准确地总结得出该性质定理的推论

.

问题4

比较上述证明方法，分析解题思路

.

师：在A字型的证明中运用了以下两种方法

.

(引导学生分析、评价解题思路，培养学生分析、评价的能力)

方法1：

运用三角形一边的平行线的性质定理，该定理从一条平行于三角形一边的直线出发，结论中的比例线段都在三角形的被截两边所在的直线上，因此，要运用该定理，需要将

DE

平移到三角形被截的边上去

.

故需增添辅助线

.

方法2：

考虑构造X型

.

或者从另一个角度思考，三角形中位线定理的证明是通过将三角形旋转180°，构造平行四边形，本题借鉴该思路

.

建立未知与已知之间的联系，将未知转化为已知来解决

.

可能选择方法2的学生较多，因为之前已经习得此方法，而方法1运用性质定理解决，为今后解决其他问题提供思路

.

师：根据相似三角形的定义，图5-3、图5-6、图5-9中△

ABC

和△

DEF

是否相似？(引导学生考虑相似问题，为后续相似三角形判定的教学埋下伏笔)生：将△

DEF

看作是△

ABC

放大(或缩小)得来的，所以△

ABC

和△

DEF

相似

.

学生根据相似三角形的定义，较易得出结论

.

师：那么，它们是否符合相似多边形的性质呢？

生：根据平行线的性质和已证得的三角形一边的平行线性质定理的推论，可知△

ABC

和△

DEF

三个角对应相等，三边对应成比例，因此，△

ABC

和△

DEF

符合相似多边形的性质

.

(强化相似性的性质，为后续相似三角形的判定打下基础)

(三)三角形一边的平行线性质定理推论的应用

1

.

在几何问题中的应用

图8

例1

已知

BE

，

CF

是△

ABC

的中线，交于点

G.

求证：对学生来说，此题运用三角形的中位线定理可以容易地证明(如图8所示，

AD

也是△

ABC

的中线)

.

师：请大家分别用文字语言和符号语言表述这一性质

.

(引导学生将符号语言与文字语言相互转化)学生的表述如表1所示

.

图9

练习1

如图9，在上述例题的基础上再次改变条件，增加两条平行线，过

G

分别作

GH

∥

AB

，

GM

∥

AC

,分别交边

BC

于点

H

，

M.

求证：通过变式练习，学生对比条件和结论的异同，找到相似之处作为突破口，增强分析问题的能力

.

2

.

在实际问题中的应用

例2

(例2为上文“情境导入”中的原题，此处略)

解：

如图1，因为

AD

∥

BC

，所以所以图像的宽=4米，图像的长=5

.

5米

.

学生学习性质定理的推论后再解决“情境导入”中的原题，问题迎刃而解

.

师：性质定理的推论不仅包含了原定理的一些结论，还拓展了原定理的结论

.

在实际生活中，还有哪些问题可以运用三角形一边平行线性质定理的推论基本图形A字型来解决？(引导学生运用已学知识反思实际生活的问题)

表1

文字语言符号语言三角形三条中线的交点叫做三角形的重心.三角形的重心到一个顶点的距离,等于它到这个顶点对边中点距离的两倍AG=2GDCG=2GFBG=2GEGD=12AGGD=13ADAG=23ADAG∶GD=2∶1GD∶AD=1∶3AG∶AD=2∶3

生：运用自己的影子来测量路灯的高度、建筑物的高度或河的宽度等

.

师：请大家根据上述例子及性质定理的基本图形(A字型图形和X型图形)自主编题，要求解题过程用到三角形一边平行线性质定理的推论，并在小组内分享自己的题目，最后每个小组选一个方案进行班级分享

.

该环节中，学生需要思考实际问题并将其与性质定理的推论结合，而自主编题要求学生在分析后对问题进行加工、再创造，难度较大，故采用小组的形式，目的是培养学生的分析、创造等高阶思维能力

.

(四)小结

师：本节课我们学习了三角形一边的平行线性质定理推论，对比三角形一边的平行线性质定理与性质定理推论的条件和结论，它们有何异同？

师：回忆推论导出的过程，我们经历了怎样的过程？是从哪种情况开始证明的？(引导学生回忆，分析证明过程)

生：从

D

，

E

是三角形的两边的中点出发，接下来考虑点

D

和

E

位置移动的一般情况，在一般情况中分别讨论

D

和

E

是三角形两边上任意一点和

D

，

E

分别是三角形两边延长线上的情况

.

师：从

D

，

E

是三角形两边的中点的特殊情况出发，再引发

D

，

E

在三角形两边上任意位置的一般情况的讨论与证明，从猜想到严格的演绎推理论证，在这个过程中我们体会了从特殊到一般以及类比归纳的数学思想

.

(进行数学思想的渗透)在考虑点

D

和

E

的位置移动的一般情况时，学生独立分析思考，画出不同的图形，体会用运动变化的观点看待问题，然后对不同图形进行分类，最后分情况证明结论

.

在分情况证明中将几何图形分解得到基本图形，再根据基本图形的性质解决问题，学生体会分类讨论及化归的数学思想

.

在探索推论的过程中，先由特殊情况(

D

，

E

是三角形两边中点)猜想哪几种图形结论成立，随后通过证明验证之前的猜想，归纳总结三角形一边的平行线性质定理推论，并对证明方法进行分析评估，体会几何演绎的思想和逻辑推理的方法

.

这也是探究性研究经历的一般过程

.

二、 分析与思考

(一)以实际问题导入引发思考

本节课以实际问题导入，问题满足三角形一边的平行线性质定理的条件，但是运用性质定理却不能解决，引发学生的认知冲突，引起学生的求知欲

.

学生体会到问题的起源，找到新知识与原有知识的联系

.

同时复习旧知，并归类基本图形，为性质定理推论的导出和证明提供途径，便于将已有的知识和经验迁移到新的知识及研究过程，为本节课的研究奠定基础

.

(二)推导过程中培养学生分析、评价的高阶思维能力

本节课在性质定理的推导过程中着重培养学生分析、评价问题的能力

.

引导学生抓住问题中关键信息“点的位置”，以此为突破口进行分析，引导学生用运动变化的观点看待问题，变化出更多样的图形，尝试综合全面地思考问题

.

在独立画图、分析思考的过程中，学生分析出可能存在的图形，教师引导学生将图形进行分类，分别考察图形的可行性，这也是分析问题必须具备的技能

.

在推导完成后，引导学生思考、评价不同的证明过程，提升学生分析和评价能力，学生经历“猜想—验证—分析论证—评估—结论决策”这一探究性研究的完整过程

.

由猜想到验证，思维反复调整

.

最后，学生体验归纳结论，从自己的语言提炼成书面语言的过程，思维不断完善，有利于思维的整合，培养思维的严密性

.

(三)在应用性质定理的过程中培养学生分析、创造的高阶思维能力

在性质定理的运用环节中，着重培养学生的分析、创造的思维能力

.

在性质定理应用中提出的实际问题正是开头情境导入环节的问题

.

在情境导入环节引导学生尝试从数学角度分析实际问题，抽象出数学图形，引发认知冲突，在应用性质定理的推论这一环节，学生再次分析问题，结合已学知识解决该问题，学生分析问题的能力得到培养

.

在关于性质定理应用的几何问题中，引导学生分析题目的条件和结论，让学生经历再创造的过程，发现三角形重心的性质

.

在自主编题环节中，学生具有更大的主动性，这一环节是学生对问题分析再创造的过程

.

学生需要思考身边的实际问题，运用已学数学知识分析实际问题，并创造性地解决实际问题

.

这一过程也能培养学生分析和创造的高阶能力，并让学生体会数学来源于生活、服务于生活

.

(四)课堂小结，反思思维过程，延伸高阶思维

课堂小结从数学知识、方法和思想方面概括本节课的内容

.

引导学生在知识方面从模糊走向清晰，从片面到全面

.

注重数学思想方法的渗透，提高学生分析评价的能力

.

反思的过程是对自身研究问题的思维过程，是对结果和思维方法等进行再认识、再评价的过程，教师培养学生的批判性思维，使思维变得越来越成熟

.