水声通信中基于均匀圆阵列的涡旋声波性能分析∗

徐 洁 李 晖 周又玲 王 萍 李 千 薛刘荀 石崇岳 王 厚

(1 海南大学信息与通信工程学院 海口 570228)

(2 南京信息工程大学滨江学院 无锡 214105)

0 引言

水声技术是海洋通信发展的一个重要技术。水声通信是研究关于如何在已知的条件下更加准确地进行水下信息的传输的一门学问。在大气中，电磁波带宽资源丰富、频段高，利用电磁波进行通信的技术已经非常成熟。但是在海水中，海水对电磁波的吸收率很大，电磁波在海水中衰减的速度非常之快，电磁信号无论是幅度还是频率都会有巨大的畸变，在海水中的传输距离非常有限[1]。

在这种情况下，水下声波成了目前有效且较为可靠的远距离信息传输媒介。虽然针对无线电的通信技术一直非常成熟，对水声通信的信息传输速率提升也有一定帮助(例如正交频分复用(OFDM)技术和多输入多输出(MIMO)技术等)，但是水声信道情况复杂，且深水与浅水情况也有所不同：海水温度、深度、洋流影响和季节变化，不同温层等因素都会影响水声通信，导致许多无线电通信方法无法正常应用于水声通信当中。尽管目前水声通信技术已经有了进步，但现在仍然不能够像无线电通信技术那样成熟与稳定，未来水声通信技术的发展还会有很大的空间[2]。

在电磁波领域中，目前产生轨道角动量(Orbit angular momentum,OAM)波束的方式主要有以下几类：透射螺旋结构[3]、透射光栅结构[4]、螺旋反射面[5]、环形行波天线[6]、天线阵列[7]、超表面材料[8]和反射阵[9]。产生OAM涡旋声波的方式一般分为两大类：有源方式和无源方式。

有源技术属于声学相控技术，原理是通过对声学换能器的独立调控来形成相控阵列，产生能够形成螺旋状的相位分布。声学中OAM 声波的有源产生方法需要昂贵的成本和复杂的电路，在高频段应用有一定的困难[10]。Hefner等[11]提出一种压电薄膜换能器产生具有螺旋波阵面的涡旋声束，证实了产生水下涡旋声波的可行性。Riaud 等[12]通过叉指换能器单元阵列，利用频域逆滤波技术能产生一定拓扑模式数的表面涡旋波。Marchiano等[13]使用压电换能器阵列可以产生高阶单一涡旋声束，并进行实验研究不同涡旋声场之间是如何进行相互作用。Demore 等[14]通过采用1000 个声源构成的天线阵列来产生比以往更加精确的涡旋声场。Berkeley 国家实验室通过有源换能器阵列，完成了涡旋声波多路复用的陆上实验，但其仅在陆地声波传输环境中进行了近距离理想仿真和实验，没有进行水下实验，无法验证水下传输的有效性。

无源材料相对有源材料来讲，产生声学OAM的方法更加简单。Ealo 等[15]提出了利用多孔铁电驻极体材料在空气中产生涡旋声场的理论方法，在高度螺旋状分布的表面上粘结多孔铁电驻极体薄膜导电胶，用脉冲信号进行驱动，实现空气中的OAM 涡旋声波，但是只能产生单频有效的涡旋波，且稳定传输具有距离限制。基于超表面结构也可以产生声学涡旋，Ye 等[16]利用一种超表面结构产生声学螺旋波；Naify 等[17]利用超材料缝隙天线产生声学螺旋波；Jiang 等[18]利用多臂螺旋裂隙板产生声学螺旋波，实验中通过调整旋臂数目，可以控制涡旋声场的阶数，并且在较长距离内也可以产生阶数稳定的涡旋声场。梁彬等[19]提出了利用超构表面对声学体系引入OAM；Li等[20]提出了利用尺度小于波长的超表面将平面波转化为带有OAM的涡旋声束，通过调节超表面材料内嵌的亚波长共鸣器腔体的轴向长度，实现对入射波的不同相位延迟，进一步实现具有涡旋声波，这一方法可以简单高效地产生声学力矩。这些方法为水下涡旋声波的低成本产生方法提供了借鉴，但结构要求高，有些要求自身具有螺旋分布的几何特征，声波能量的透射效率也有所限制，很难进行性能分析研究。为研究OAM涡旋声波的产生并进行涡旋声波性能分析，本文利用有源技术中的换能器阵列来模拟产生OAM 涡旋声波。

对光学中OAM波束的研究可知，随着OAM拓扑模式数l增大，主瓣夹角变宽，即最大增益的方向角变宽。有学者已经通过仿真验证过，当阵列单元数N=12 时产生4 种OAM 拓扑模式下的辐射光束：当OAM拓扑模式数l=1 时，主瓣夹角较小，约为60◦；而随着拓扑模式数l的增大，主瓣夹角逐渐增大；当l=4时，主瓣夹角约为120◦[21]。

由以往的研究可知，现阶段能产生声学涡旋的形式有多样，通常采用大数模换能器阵列来产生具有不同函数的特定声场，如拉盖尔高斯(L-G,Laguerre-Gauss)型和贝塞尔(Bessel) 函数型。但在水下声场中，以往研究对阵列单元数目、阵列半径、声波频率等对生成的OAM 主瓣夹角以及幅值的影响，并未进行详细的性能分析。

本文通过声波换能器阵列产生水下OAM涡旋声波，分析声波辐射源数量、圆形阵列构型与不同拓扑模式l之间的对应关系：首先生成各种单模式的OAM 波束，进行单模式OAM 涡旋声波的检测；然后确定OAM 拓扑模式与换能器阵列之间的一一对应关系，生成不同模式下的涡旋声波，给出阵列单元数目、阵列半径、声波频率等对生成的不同拓扑模式下涡旋声波的影响。

1 轨道角动量理论基础

在量子力学和经典电动力学的研究中已经证实，电磁波的波动传输，不仅含有动量还有能量，电磁波动量又分为线动量P和角动量J，线动量和角动量的关系为

其中，r表示位置矢量。线动量与平移和力的作用有关，其表达式如下：

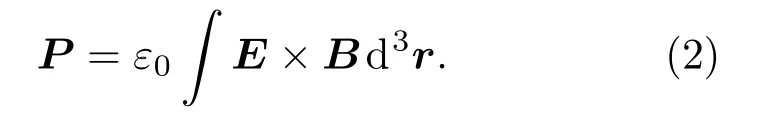
角动量由旋转和扭矩作用决定，表达式如下：

其中，S表示自旋角动量(Spin angular momentum,SAM)，描述电磁场旋转自由度的固有属性，表示粒子的极化，S=+1，表示左旋圆极化；而S=−1 时，表示右旋圆极化。L表示OAM的拓扑模式数，它表示粒子绕传播轴旋转，与电磁波的相位波前分布有关[22−23]。轨道角动量的本征态可以定义为量化的拓扑电荷数，具有相位因子e−ilφ，在相位因子的作用下，电磁波的相位由平面结构转变为具有螺旋的波前相位，并且波前相位沿着涡流中心的传播轴旋转，绕着传播轴旋转一周，相位变化2πl[24]。

声波的波动传输与光波的传输特性相似，涡旋声波同样具有相位因子e−ilφ，但是与涡旋光波不同的是，涡旋声波不存在自旋效应和偏振效应，涡旋声波不携带自旋角动量SAM，只携带轨道角动量OAM[25−26]。OAM涡旋声波一般具有4个特性：沿传播方向场强为零、相位在[0,±2πl]内分布、传输过程中波形具有自我修正能力以及将力矩传递给其他物质使其旋转[27]。

通过天线阵列产生的Bessel 型涡旋波束的相位结构具有依赖性方位角，N个天线单元组成的均匀圆阵(Uniform circular array,UCA)矢势表达式为

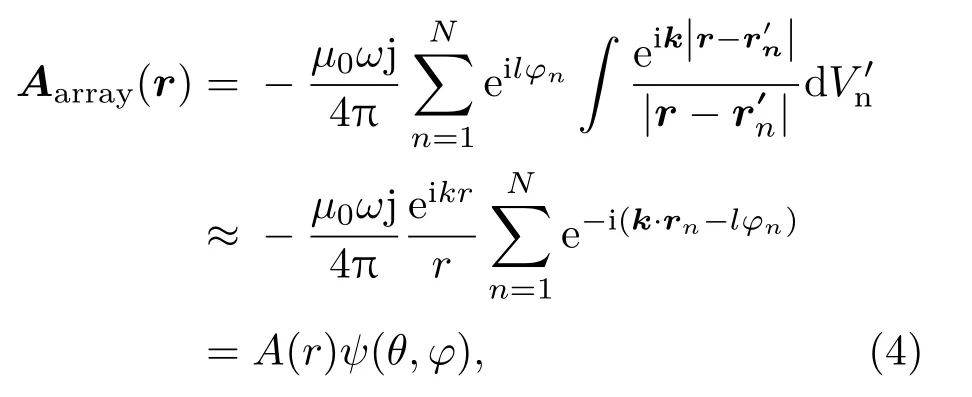
式(4)中，A(r)对应天线单元的幅度，ψ(θ,φ)为UCA的阵列因子，利用相位角积分可近似为

电场表示为

从公式(4)和公式(5)中可以得出，通过对阵列半径和激励信号幅度的设计，可以有效控制不同OAM 模式的强度分布，将不同拓扑模式涡旋波束的主瓣对准到相同的仰角方向，同时无需改变相位角分布。增加阵列直径，虽然在减小增益角度的同时旁瓣的数目有所增加，能量也有一部分的损失，但增加的旁瓣角度比主瓣宽很多，并且旁瓣增益也比主瓣弱很多，所以产生的影响在实际检测过程中并不重要[28−29]。

对L-G 型OAM 波束具有e−jlφ的依赖性方位角，在柱坐标下场分布的表达式如(7)所示：

其中，r表示检测点到辐射轴的辐射距离，φ表示方位角，z表示传播距离；w(z)代表z处的波束宽度，ω0为束腰半径，zR=πω0/λ表示Rayleigh 距离，λ为波长；Cpl为拓扑模式的能量分配系数A为总辐射能量[29−31]；Llp代表一般Laguerre 多项式，k表示波矢量，k=2π/λ，l=1,2,···,L表示拓扑模式数，p表示径向节点数。

经过研究证明，通过水声换能器能够产生涡旋声波OAM，将N个换能器单元以相同间隔的相位角均匀地放置在半径为a的圆周上，以相同频率、相同相位差的信号源接入换能器单元[32−33]。

2 阵列单元设计

如图1所示，空间坐标角上角距间隔为∆φ=2π/N，第n个换能器单元的坐标位置为Tn(a,φ0n,0)，其中φ0n=(n−1)∆φ=(n−1)2π/N。对具有固定相位差∆ϕl=2πl/N的单频信号源，N个换能器总相位差为2πl，声源数N和拓扑模式数l之间的限制关系为

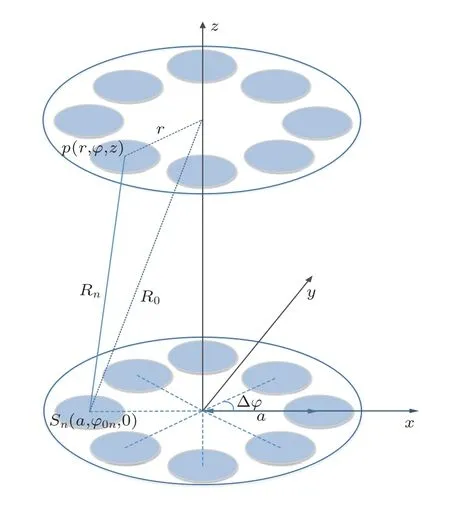
图1 单一模式轨道角动量的UCA 设计图Fig.1 UCA design drawing of single-mode orbital angular momentum

即为产生拓扑模式l的涡旋声波，至少需要的换能器单元数目为Nmin=max(2|l|+1,4)[34]。由第n个换能器单元产生的声压可以表示为

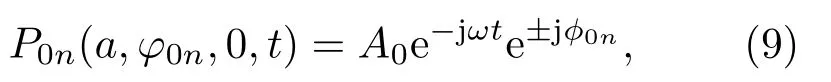
其中，A0、ω、ϕ0n分别表示幅度、角频率和初始频率。在阵列平面的上方位置p(r,φ,z)处，由第n个换能器单元产生的声强为

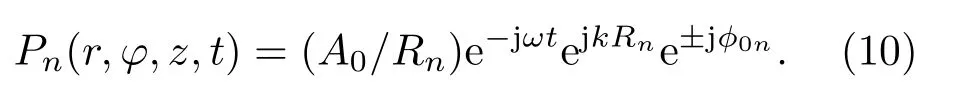
所以整个UCA 阵列在位置p(r,φ,z)处 的场强为

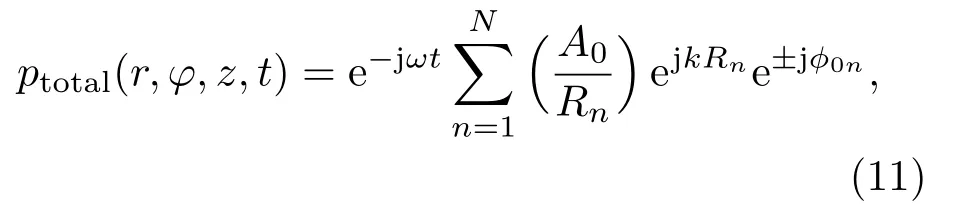
其中，Rn代表传播距离，Rn=[(rcosφ−acosφ0n)2+ (rsinφ−asinφ0n)2+z2]−1。由公式(6)可知，OAM 螺旋波束具有内在的正交特性，即两个OAM 波束幅度的标量积为

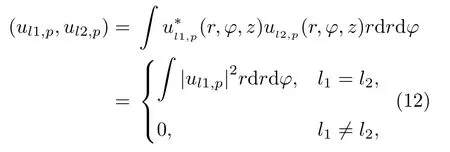
式(12)说明对于任意两个不同模式(l1≠l2)的OAM 波束ul1,p和ul2,p，当p为固定值时，理论上两者的相关度为0，即满足相互正交特性[35]。

根据涡旋声波的声场理论，采用仿真软件分析L-G 型涡旋波束的时空分布，通过对波束幅度和相位的分析，得到幅度、相位以及波束归一化方向图，基于得到的幅度、相位、归一化方向图，进一步分析声波辐射源数量、辐射声源频率、圆形阵列构型对不同拓扑模式数的涡旋声波的性能影响。

3 仿真模拟与分析

根据图1，模拟柱坐标下换能器阵列产生的L-G 型OAM 波束，并在仿真软件中进行仿真，得到L-G 型涡旋声波OAM 的时空分布以及幅度、相位、主瓣波束图。设置阵列单元数N=10、频率f=30 kHz、阵列半径a=3λ时，得到该参数下l=1、l=2、l=3、l=4，4 种不同拓扑模式数的涡旋声波的时空分布以及幅度和相位图。

在进行仿真实际时，首先预先设置阵列构型参数阵列单元数N、阵列半径a、换能器信号频率f等，仿真参数设置和含义解释如表1所示。其次，利用for循环函数设置换能器初始相位差，根据公式求出换能器的笛卡尔坐标表示，根据公式(7)模拟预设参数下L-G 型的声涡旋分布表达式，求出表达式下的幅值与角度分量，利用画图函数画出各个分量所对应的幅度和相位图，对所求的声压幅值进行归一化处理，再在极坐标下画出归一化声压幅值，得到归一化方向图。

表1 仿真参数设置及含义解释Table 1 Simulation parameter setting and meaning explanation

图2是4 种不同模式数(模式数l分别为1、2、3、4)下的涡旋声波的时空分布以及幅度和相位图。图2(a)为时空分布图，其中横纵坐标表示辐射距离，单位为m，z轴坐标表示声压幅值大小，单位为Pa，可以看出随着拓扑模式数的增加，主瓣波束变宽，即主瓣波束角增大，而主瓣峰值略有减小。图2(b)为涡旋声波的幅度图，横纵坐标表示辐射距离，颜色标尺从上到下表示幅值大小，可以看出中心位置的幅度非常小，即存在相位奇点。图2(c)给出的是涡旋声波的相位图，横纵坐标表示辐射距离，颜色标尺从上到下表示π到−π，可以看出图2(c1) 中有一个涡旋，可知产生了模式数l=1 的OAM；图2(c2)中有两个涡旋，即产生了模式数l=2 的OAM，图2(c3)中有3 个涡旋，即产生了模式数l=3 的OAM，图2(c4)中有4 个涡旋，即产生了模式数l=4 的OAM。在保持参数条件不变下，给出涡旋声波的主瓣峰值以及主瓣波束角方向图，如图3所示。

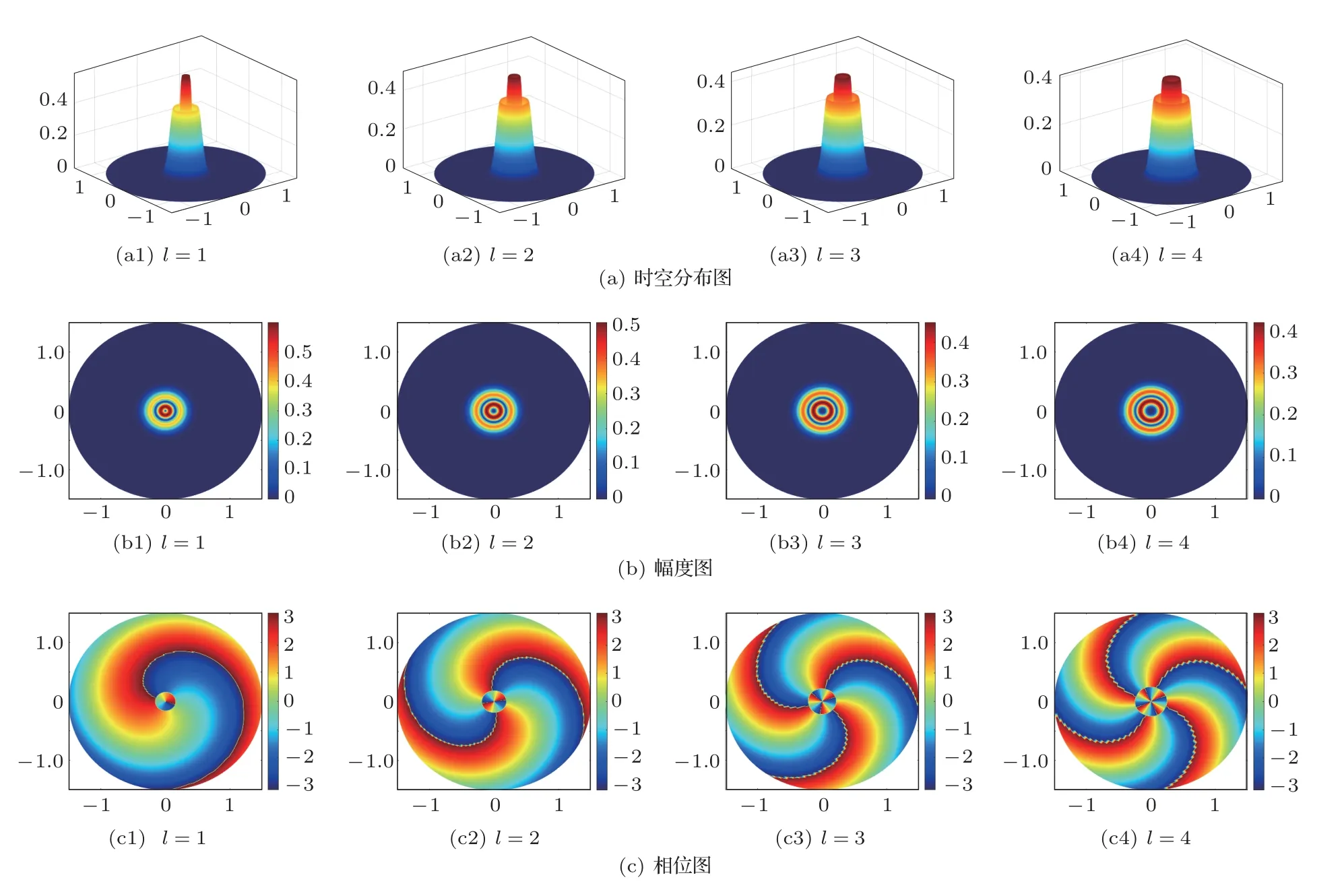
图2 4 种模式数下的涡旋声波时空分布以及幅度和相位图Fig.2 Spatiotemporal distribution,amplitude and phase diagrams of vortex acoustic waves with four modes

图3(a)为模式数l=1 时的涡旋声波峰值及方向图，主瓣峰值约为0.6，主瓣波束角约为8.6◦；图3(b)为模式数l=2 时，涡旋声波的主瓣峰值约为0.5，主瓣波束角约为12◦；图3(c)为模式数l=3 时的涡旋声波峰值及方向图，主瓣峰值约为0.45，主瓣波束角约为15.5◦；图3(d)为模式数l=4时，涡旋声波的主瓣峰值约为0.45，主瓣波束角约为18.9◦。从图3中可以明显地看出，随着拓扑模式数的增大，产生的涡旋声波主瓣波束角增大，主瓣峰值减小。

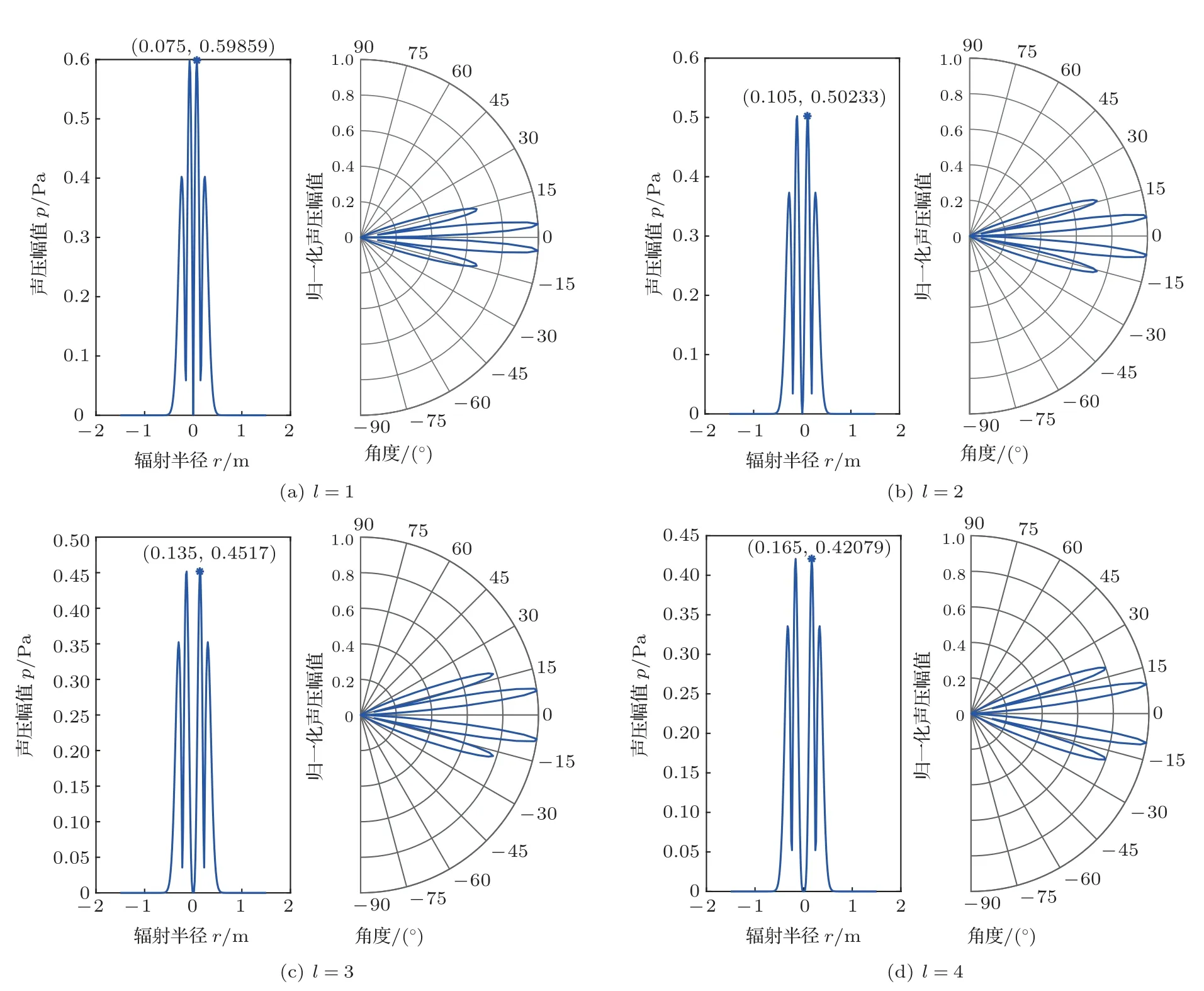
图3 不同模式数下的涡旋声波峰值及方向图Fig.3 Vortex acoustic wave peaks and patterns of different modes

图4为UCA 阵列单元数N=12、f=15 kHz、OAM 模式数l=1 时，阵列半径变化的归一化方向图。随着阵列半径的变化，图4(a)～图4(d)的阵列半径从λ/2 变化到2λ，可以看出生成的OAM 主瓣波束角逐渐增大，同时旁瓣夹角也增大。

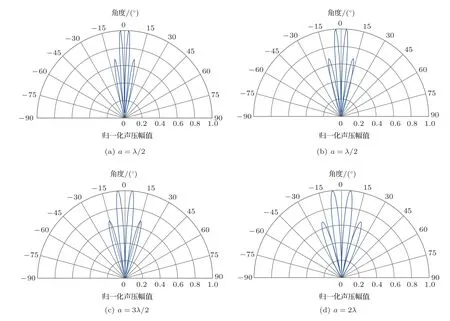
图4 UCA 归一化方向性图随半径变化Fig.4 UCA normalized directivity map changes with radius

在以往的研究里，在电磁波段，基于天线阵列的OAM 涡旋波束中，设置UCA 阵列半径从λ/2 增大到2λ，随着阵列半径增大，主瓣的能量更加集中，但旁瓣的影响也随之增加，旁瓣数目增加同时旁瓣能量也增大，对其他拓扑模式的干扰也更大。

在本文的研究中，模拟柱坐标下水声换能器阵列产生的L-G 型OAM 波束，发现随着阵列半径从λ/2 增大到2λ，主瓣波束角增大，主瓣能量发散，同时旁瓣夹角明显增大，旁瓣能量发散，但是旁瓣的数目并无增加。在进一步的研究中发现，L-G 型涡旋波束的旁瓣数目与式(6)中的径向节点数p有关，设置阵列单元数N=12、f=15 kHz、OAM 模式数l=1，当径向节点数p=1 时，有一个旁瓣，如图5(a)中所示；当径向节点数p=2时，有两个旁瓣，如图5(b)中所示。可以看出，当径向节点数增加时，主瓣的能量集中，旁瓣数目增加，旁瓣能量发散。

图5 两种不同径向节点数的归一化方向性图Fig.5 Two normalized directional graphs with different numbers of radial nodes

在进一步的研究中，给出不同参数条件下的OAM 声波的主瓣峰值以及主瓣波束角，通过分析比较阵列单元数、阵列半径、频率等对产生的轨道角动量的最大幅值以及主瓣波束角的影响，见图6～8。

首先，在频率f=30 kHz、换能器阵列单元数N=10 的条件下，分别仿真出轨道角动量模式数l=1,2,3,4 的OAM 涡旋声波；然后设置阵列半径a ∈[0.5λ,10λ]，记录下主瓣波束角以及主瓣峰值随阵列半径的变化趋势。图6(a)为主瓣波束角的影响图，可以看出同样的参数条件下，模式数越高，主瓣波束角越大；并且随着阵列半径的增大，主瓣波束角增大；在模式数l=4下，这种增加的趋势更加明显。图6(b)为主瓣峰值的影响图，可见同等参数条件下，模式下越高，主瓣峰值越小；而随着阵列半径的增大，主瓣峰值减小，并且两种模式数下的减小趋势无明显差异。

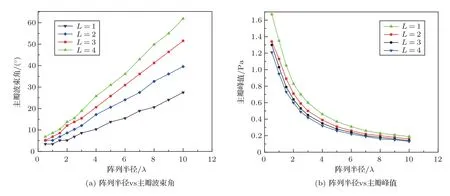
图6 阵列半径与主瓣波束角和峰值关系Fig.6 The relationship between array radius and main lobe beam angle and peak value

保持换能器阵列单元数N=10，设置阵列半径a=3λ，频率从10 kHz增加到150 kHz，分别仿真出轨道角动量模式数l=1,2,3,4 的OAM 涡旋声波，并画出主瓣波束角和主瓣峰值随频率的变化趋势。图7(a)为频率对主瓣波束角的影响图，可以看出，主瓣波束角随着频率的增大而减小，同样在模式数l=4时，这种减小的趋势更加明显。图7(b) 为频率对主瓣峰值的影响图，可以看出，模式数l=1 时的主瓣峰值更高，随着频率的增大，由纵坐标中可以看出，两种模式数的主瓣峰值的变化均在0.05 之内，主瓣峰值的变化趋势不明显。

图7 频率与主瓣波束角和峰值关系Fig.7 The relationship between frequency and main lobe beam angle and peak value

保持阵列半径a=3λ，设置频率f=30 kHz，将换能器阵列单元数N ∈[10,20]，依次仿真出轨道角动量模式数l=1,2,3,4 的OAM 涡旋声波，记录下4 种模式数的主瓣波束角和主瓣峰值随阵列单元数的变化趋势。图8(a)为阵列单元数对主瓣波束角的影响图，能明显看到不同模式数的主瓣波束角不同，但是都不会受阵列单元数影响。图8(b)为阵列单元数对主瓣峰值的影响图，还可以发现，主瓣峰值随着阵列单元数的增加而增大，并且低阶模式数时效果更加明显，从功率分配系数Cpl来看，ulp幅值大小与阵列单元数N成正比关系，从仿真结果中也可以得到验证，与仿真图中一致。

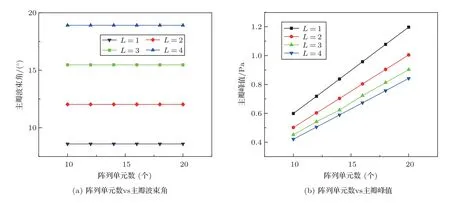
图8 阵列单元数与主瓣波束角和峰值关系Fig.8 The relationship between the number of array elements and the main lobe beam angle and peak value

4 结论

本文研究通过水声换能器阵列产生L-G 型OAM 涡旋声波，分析阵列半径、频率、阵列单元数等对产生的OAM涡旋声波的性能影响。首先，通过N个换能器以相同相位差均匀地放在半径为a的圆周上，以相同频率、相同相位差的信号源接入换能器，模拟出OAM涡旋声波。然后依次对阵列半径、频率、阵列单元数等参数影响进行分析并得出结论。模式数越高，主瓣波束角越大，主瓣峰值越小。阵列半径越大，主瓣波束角越大，并且在模式数高时更加明显，而主瓣峰值则随着阵列半径的增大而减小；频率越高，主瓣波束角越小，主瓣峰值变化不大；阵列单元数对主瓣波束角无影响，但与主瓣峰值成正比关系，阵列单元数越多，主瓣峰值越大。

目前本文通过模拟换能器产生OAM 涡旋声波，给出它的三维时空图以及幅度和相位图，然后进一步分析了阵列单元数、阵列半径、以及频率对涡旋声波的主瓣波束角以及峰值的影响。未来的工作将通过FPGA 调制水声换能器所需的同频固定相位差的信号源，接入水声换能器中产生实际涡旋声波信号并通过水听器进行接收检测，同时进一步验证阵列半径、单元数、频率等对主瓣波束角和峰值实际影响。

当前的仿真是针对理想信道的理论验证，对标的是实验室水箱静态水环境，以便于与参考文献中的仿真结果进行比较(参考文献中的数据也多是基于实验室水箱理想信道环境的)；未来将在室外开放海水环境中，开展实际水声信道的性能分析、算法修正和实验验证工作。另外，实验团队已经就不同场景下的水声信道环境进行了建模仿真，数据收集和试验验证工作。