一种新型的水下低频共鸣器∗
邱燕萍 周浩萌 寻天雨 郁高坤
(中国海洋大学 青岛 266100)
0 引言
声音对海洋动物的生存非常重要。近年来由人类活动产生的水下噪声严重地破坏了海洋环境平衡,正在威胁着海洋哺乳动物及其他水生生物的生命健康,引起了广泛的关注。由人为活动产生的噪声包括船舶噪声、声呐工程噪声以及水下作业平台噪声等,对海洋哺乳动物的危害主要有生理损伤、生理功能障碍和行为改变[1]。目前人们在呼吁各国联合制定与海洋噪声污染相关的法律、规范来保护海洋生物的同时,还从降噪的角度出发,致力于研究削弱噪声机制以降低污染影响,其中比较成熟的方法是利用气泡进行水下低频声降噪[2−3]。但是气泡的抗压性差,并不适用于高压的水下环境,因此设计一种具备耐压性的水下低频共鸣器十分必要。
亥姆霍兹共鸣器[4−5]作为经典的声学共振结构,通常由一个腔体和一个与外界连通的小孔组成,因其结构简单、声学效果显著而被人们广泛应用于噪声控制等领域。目前已经有不少研究者用它进行改良构造成亚波长的完美吸收体[6−9],或者将其按照一定的规律进行排列组成声学超构材料[10]来实现对声波和弹性波的调控。但是亥姆霍兹共鸣器也存在其固有缺陷[11],比如对频率的选择性很强。虽然在共振频率处,亥姆霍兹共鸣器的消声效果很好,但工作频段受品质因素影响大,一旦稍微超出范围,消声量便会快速下降,同时受到自身结构限制,其低频消声效果不理想。特别是在水下环境中,还要考虑材料特性阻抗、耐压性等问题,应用起来并非易事。
本文主要基于共振理念提出了在宽开口的刚性腔体内嵌入聚氨酯泡沫来构造一种新型的水下共鸣器,以实现低频共振、品质因素低的效果。首先是掌握聚氨酯泡沫必要的声学参数。在此基础上建立镶嵌聚氨酯泡沫共鸣器的理论模型,根据声场形式获得相应的声阻抗率和共振频率,并对模型进行简化检验,建立集中参数系统分析其共振机制,解释镶嵌聚氨酯泡沫的共鸣器能够降低共振频率、维持较小品质因素的原因。最后利用辐射阻抗对理论模型的共振频率进行补充修正,运用有限元软件完成建模仿真工作,与理论模型作对比。
1 聚氨酯泡沫的声速测定
聚氨酯泡沫塑料是一种非常受欢迎的吸声材料,具有质量轻、易成型、适用范围广等优点。要想将聚氨酯泡沫应用到声学设计之中,掌握其声学特性十分必要。而聚氨酯泡沫塑料泊松比满足Kerner-Rusch经验公式[12]:
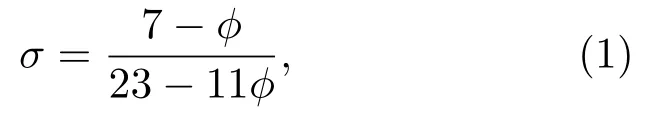
其中,ϕ=ρavg/ρs是基体材料体积比,ρs和ρavg分别是基体材料和泡沫塑料的密度。根据文献[13],假设E0是聚氨酯基体材料的杨氏模量,那么聚氨酯泡沫杨氏模量Ef的预测可以采用公式(2):
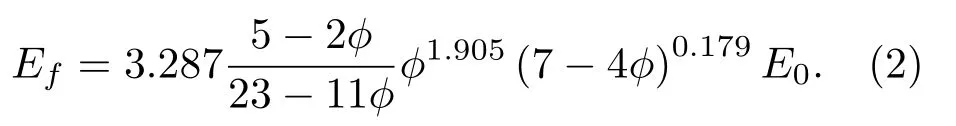
聚氨酯泡沫的纵波声速和横波声速为
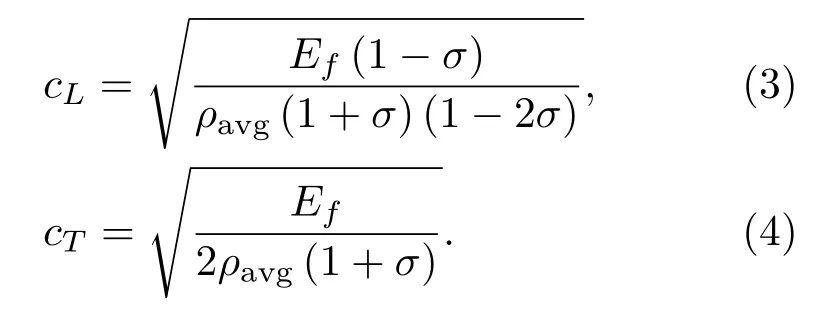
已知聚氨酯基体材料的杨氏模量为E0=2433 MPa,密度为ρs=1200 kg·m−3。如果这时知道聚氨酯泡沫的密度,就可以根据式(1)计算泊松比,再根据式(2)得到杨氏模量,进而代入式(3)和式(4)获得相应的纵波声速和横波声速,具体的参数理论估算结果见表1。

表1 聚氨酯泡沫参数理论估算结果Table 1 Theoretical estimated results for the parameters of polyurethane foam
因为聚氨酯泡沫的声速参数关系到后续的理论建模以及将来的实验研究,所以还需要通过水池实验测定。在实验中,可以由两个水听器之间有无聚氨酯泡沫板的时间差以及板的厚度来计算聚氨酯泡沫的声速,具体操作如图1所示。在实验过程中,声源、水听器的声中心、聚氨酯泡沫板的几何中心要在同一水平线上,确保声波能够垂直穿过聚氨酯泡沫板。

图1 聚氨酯泡沫声速测量实验示意图Fig.1 Schematic diagram of sound velocity measurement for polyurethane foam
假设两个水听器之间的距离记为l,聚氨酯泡沫板的厚度为d,没有聚氨酯泡沫板时两个水听器接收到声波的时间差记为t1,则水的声速有

当聚氨酯泡沫板存在时,两个水听器接收到声波的时间差记为t2,其声速测量方程可整理为
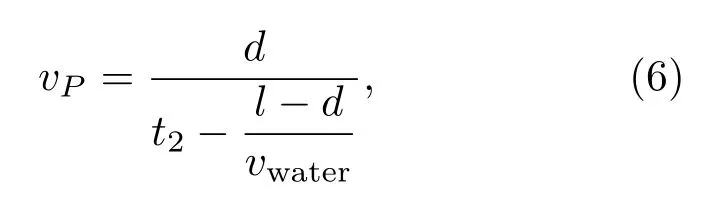
其中,d=0.07 m,时间差t1、t2可以通过水听器信号分别与功放信号做相关处理后做差获得。考虑到声波衍射以及水面散射的影响,两个水听器的距离应该尽可能接近,所以在实验过程中l主要采用了0.35 m和0.45 m两个距离。
为了保证实验结果的正确性,选取4 天不同的时间段进行多次测量,具体处理结果见表2。其中聚氨酯泡沫的纵波声速可以直接由实验测量得到。而横波速度无法直接测量,所以需要先通过式(3)计算出对应的杨氏模量,再根据式(4)获得。最后对这4 天的测量结果取平均,聚氨酯泡沫的纵波声速为970.75 m/s,横波声速为495.33 m/s,与理论估算结果差不多,符合镶嵌聚氨酯泡沫共鸣器结构设计的预期要求。

表2 聚氨酯泡沫声速测量处理结果Table 2 Measured sound velocity of polyurethane foam
2 建立镶嵌聚氨酯泡沫的水下共鸣器理论模型
2.1 理论模型
求解声场的理论解法主要有积分方程法和分离变量法[14]。通常认为,分离变量法适用于求解有界空间的定解问题,而积分变换法则适用于求解无界空间的定解问题。通常严格理论解只针对规则目标,对于现实中比较复杂的散射体,则需要用到近似解析法和数值解法。图2是本文设计的镶嵌聚氨酯泡沫共鸣器结构,腔壁用钢制备,中心的圆柱弹性体则为聚氨酯泡沫,其中腔体高度记为h,腔体半径记为b,钢壁厚度记为q,聚氨酯泡沫的半径记为a。在建立理论模型时,假定水为理想流体,聚氨酯泡沫所制成的弹性圆柱体为理想弹性体,腔壁刚性,声波的传播绝热且结构上界面处的声压均匀分布。
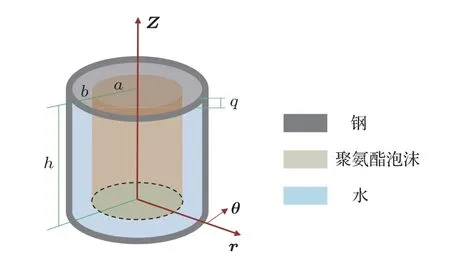
图2 镶嵌聚氨酯泡沫的水下共鸣器Fig.2 An underwater resonator embedded with polyurethane foam
已知标量势函数Φ和矢量势函数Ψ可以分别描述固体中的纵波和横波[15]。因此由氨酯泡沫所制成的弹性体中的声场满足关于标量势和矢量势的两个方程:
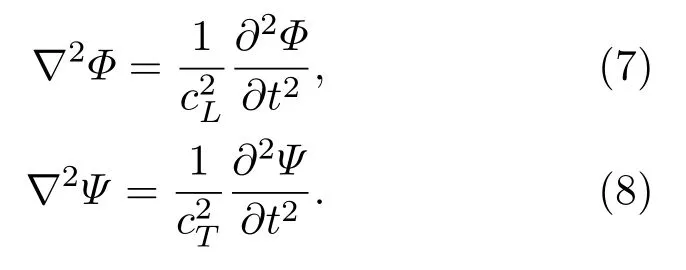
弹性体周围的水中声场p满足理想流体中的波动方程:
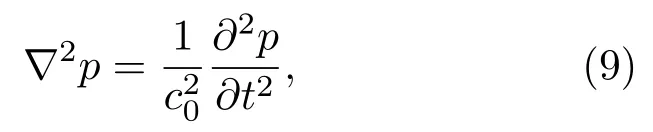
其中,c0是水的声速。因为Laplace算子在柱坐标系下的形式为

而当Laplace 算子在柱坐标系下作用于一个矢量F时有
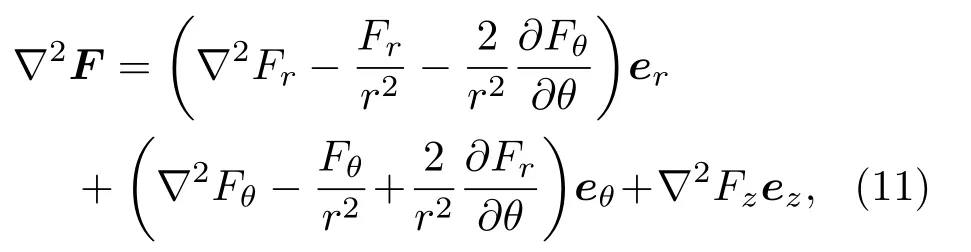
利用Laplace 算子对式(7)、式(8)、式(9)展开,应用积分变换法,代入边界条件即可求解声场[16−17]。忽略时间因子e−jωt并假定腔体声场呈轴对称分布,在z轴方向上对声场做傅里叶展开,则聚氨酯泡沫弹性棒的纵波、横波及其周围水中的声场可以整理为以下积分形式
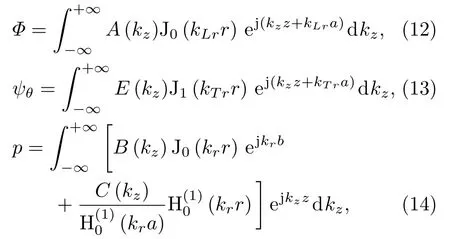
共鸣器声场模型的边界条件考虑了声波在不同媒质之间界面上的反射、折射与透射,结合图2镶嵌聚氨酯泡沫共鸣器的结构特点,本文将涉及到的边界条件整理归纳成表3。根据表3,只需要将边界条件逐一代入声场函数表达式就可以列出各个系数之间的方程组,然后进行联立求解即可。注意在求解声场展开系数的超定方程组时需要用到对角加载奇异值分解方法[18]提高数值稳定性。

表3 边界条件Table 3 Boundary conditions
对于理论模型而言,假定镶嵌聚氨酯泡沫共鸣器开口处的声压是均匀的,则该处质点振速分布v(r)的形式可以写为

其中,ρ0表示的是水的密度。此时质点振速分布与径向位置有关,对其取平均就可以得到共鸣器开口处的平均质点振速:

如果在边界条件中设定开口处的声压为1,则声阻抗率可以写为

当共鸣器发生共振时,声阻抗率的虚部为零,也就是说声阻抗率虚部为零时所对应的频率值即为共鸣器的共振频率。
2.2 声场模型的简化检验
为了确保镶嵌聚氨酯泡沫共鸣器理论模型的正确性,有必要对结构中的声场模型进行简化检验,所谓简化就是在建模过程用到的近似处理。如果镶嵌聚氨酯泡沫共鸣器的理论模型成立,那么它理应能够描述一些在原结构基础上简化而来的声场模式,这里主要考虑了聚氨酯泡沫趋于无以及聚氨酯泡沫趋于填满整个共鸣腔两种情况分别用于检验水中声场模式与聚氨酯泡沫弹性体声场模式。
首先是水中声场模式的检验。当共鸣腔内的聚氨酯泡沫半径趋于无穷小时,模型近似于末端被封闭的有限长直管。而末端被封闭的有限长直管可以直接利用阻抗转移公式得到开口处的声阻抗率:
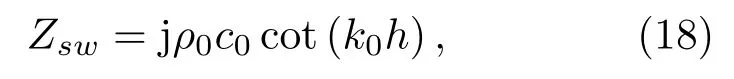
其中,k0=ω/c0。此时将聚氨酯泡沫半径趋于0 时的理论模型的声阻抗率与直管结构的声阻抗率进行对比,若是能够对应吻合,则可验证模型正确。而且为了说明一般性,本文假设所有的声速量和密度量均以水为参考进行归一化,而所有的结构长度量都以腔体半径作为参考。
图3是当镶嵌聚氨酯泡沫共鸣器的腔体半径b=0.5,聚氨酯泡沫半径a=0.0001,不同腔体高度的理论模型与对应高度的直管结构的声阻抗率对比结果,其中星号、圈、四方形、五角星标记代表h依次取值为0.3、0.4、0.5、0.6时的理论模型的声阻抗率,红色、绿色、玫红色、黄色实线则为相应高度直管的声阻抗率,二者几乎对应重合。而且通过理论模型计算出来的声阻抗率的实部均远远小于与其相对应的虚部,所以可以忽略实部将声阻抗率看成一个纯虚数,这在形式上与式(18)一致。从这两点来看,水中声场的建模成立。
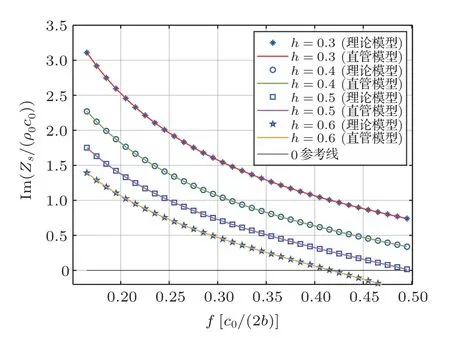
图3 理论模型与直管模型声阻抗率对比Fig.3 Comparison of specific acoustic impedance between the theoretical model and a tube model
然后是聚氨酯泡沫弹性体声场模式的检验。当聚氨酯泡沫的半径趋于腔体半径时,模型近似于一端固定、一端受到均匀声压作用的棒。为了更好地贴合实际棒振动情况,本文从棒的纵振动方程出发,同时考虑径向运动,得到弹性体顶端处的声阻抗率为
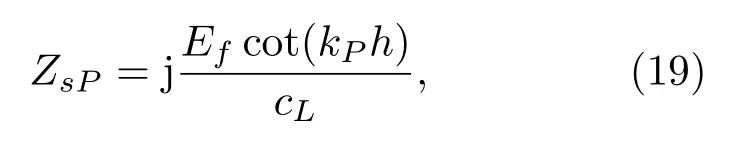
其中,kP是聚氨酯泡沫的纵波波数,而Ef=ρavgc2L是聚氨酯泡沫的等效杨氏模量。然后将聚氨酯半径接近腔体半径的理论模型的声阻抗率与棒纵振动的声阻抗率进行对比,观察二者是否一致。
图4是当镶嵌聚氨酯泡沫共鸣器的腔体半径b=0.5,聚氨酯泡沫半径a=0.4999,不同腔体高度的理论模型与对应高度的弹性棒纵振动模型的声阻抗率对比结果,其中星号、圈、四方形、五角星标记代表h依次取值为0.3、0.4、0.5、0.6 时的理论模型的声阻抗率,红色、绿色、玫红色、黄色实线则为相应高度弹性棒纵振动的声阻抗率,二者也几乎对应吻合。而且同样的,由理论模型计算出来的声阻抗率实部很小,可以舍去不计,只考虑虚部情况即可,其声阻抗率在形式上与式(19)一致。说明了聚氨酯泡沫弹性体声场模式正确。
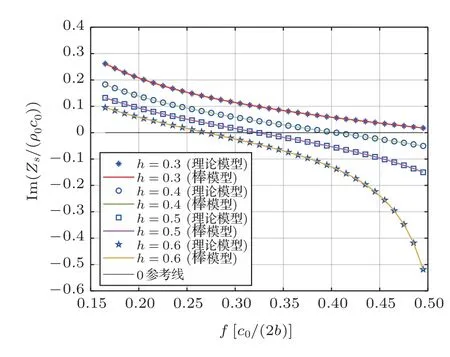
图4 理论模型与棒纵振动模型声阻抗率对比Fig.4 Comparison of specific acoustic impedance between the theoretical model and the longitudinal vibration model of a rod
从水中声场以及聚氨酯泡沫弹性体声场模型的检验结果来看,镶嵌聚氨酯泡沫共鸣器的理论模型完全可以描述两种极端假设下的声场情形,且模型的求解结果与严格的理论值高度吻合。由此可以认为,本文所建立的关于镶嵌聚氨酯泡沫的共鸣腔内声场的理论模型是正确的。
2.3 建立镶嵌聚氨酯泡沫的水下共鸣器的集中参数模型
本文在2.2 节声场模型的简化检验中讨论了直管结构以及棒纵振动的声阻抗率,证明了理论模型的正确性,但实际上镶嵌聚氨酯泡沫共鸣器的声阻抗率应该由水和聚氨酯泡沫弹性体共同决定。由于镶嵌聚氨酯泡沫共鸣器的整体尺寸远小于本文所关心频段的波长,故在描述其声学特性时,还能够采用建立集中参数等效模型的方法。这时镶嵌聚氨酯泡沫共鸣器开口处的声阻抗可以用水中声场在管口处的声阻抗与弹性棒纵振动自由端的声阻抗并联的形式来进行等效。
因为聚氨酯泡沫的存在,开口处的水呈环形分布,故在管口处水贡献的声阻抗为

聚氨酯泡沫贡献的声阻抗为
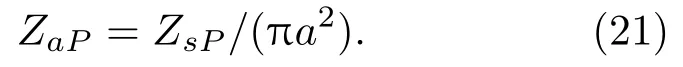
由并联规律求出该理论下开口处总的声阻抗为

或者用声阻抗率来表示:

与简化检验时的做法一样,继续将理论模型和并联模型的声阻抗率进行对比。
图5是当镶嵌聚氨酯泡沫共鸣器的腔体半径b=0.5,腔体高度h=0.5,不同半径的聚氨酯泡沫的理论模型与并联模型声阻抗率对比结果,其中星号、圈、四方形标记代表a依次取值为0.25、0.35、0.45 时的理论模型的声阻抗率,红色、绿色、玫红色实线则为相应并联模型的声阻抗率,二者在数值以及走势方面都高度一致,说明了并联模型的猜想正确。

图5 理论模型与并联结构模型声阻抗率对比Fig.5 Comparison of specific acoustic impedance between the theoretical model and a parallel model
除此之外建立集中参数系统也有利于继续讨论分析内嵌聚氨酯泡沫对共鸣器共振机制的影响。所以继续对结构开口处的声阻抗率式(23)进行展开:

当Zst=0 时,得到或者其中n=,1,2,...。由这两个等式求得两类共振频率,分别记为frw和frP,则有

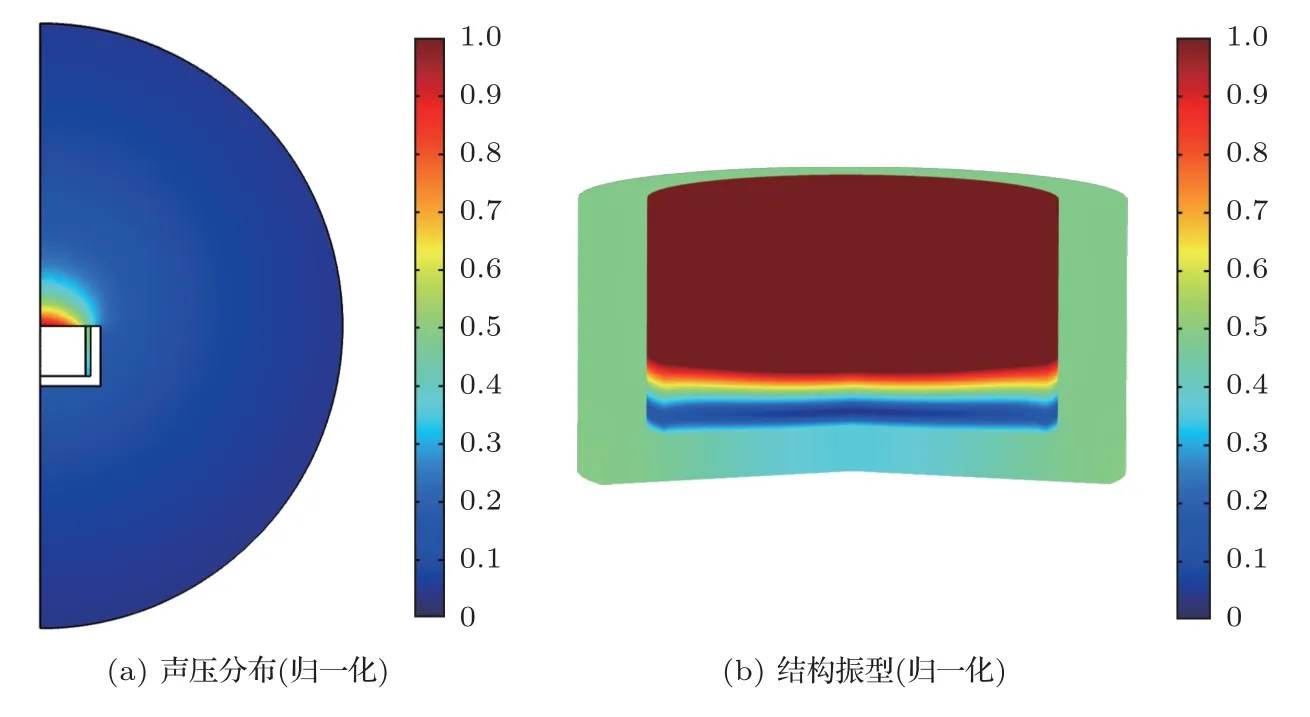
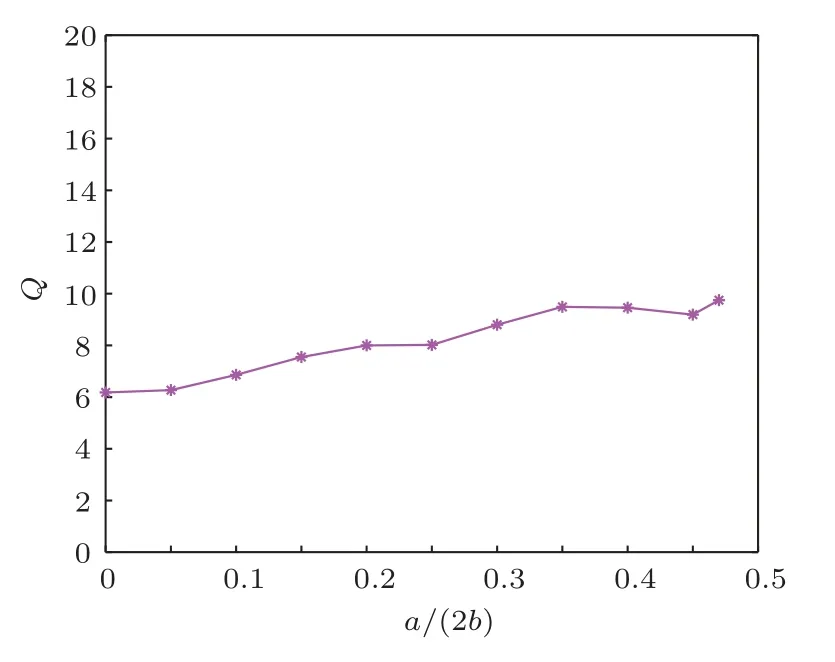
其中,frw是没有聚氨酯泡沫时大开口共鸣器的共振频率,而frP则是纯聚氨酯泡沫弹性棒做纵振动时的共振频率。由于cL 从另一个角度来看,聚氨酯泡沫的存在可以增大共鸣器的声容。由式(18)和式(24)可以分别得到无聚氨酯泡沫和有聚氨酯泡沫时共鸣器的声阻抗率。当结构作为低频散射体存在时,对其做泰勒展开,并只取第一项做近似得到 进而得到二者的声容: 为了比较无聚氨酯泡沫时共鸣器腔体的声容和有聚氨酯泡沫时共鸣器腔体声容的大小,将这二者做差∆=Cat−Caw并化简得到 因为前面在对聚氨酯泡沫做声速测定的时候,已经知道c20ρ0>Ef,所以∆>0,严格证明嵌入聚氨酯泡沫确实使得声容变大了。 前面已经建立了镶嵌聚氨酯泡沫共鸣器的理论模型,并做了大量的理论分析和检验,本节主要应用有限元软件进行建模仿真以实现进一步的验证,更好地分析镶嵌聚氨酯泡沫共鸣器的声学特性。 考虑到现实中共鸣器是作为水下散射体存在的,整个水下环境可以被认为是无限大的自由空间,声场模态均需要外界入射声波的激励才能产生,此时共鸣器中的水和聚氨酯泡沫弹性体会发生振动,并向外辐射声能量。辐射抗作为同振质量的存在对系统的共振频率影响很大,所以在描述镶嵌聚氨酯泡沫共鸣器的散射特性时,需要加上辐射阻抗。假定平面波沿轴向入射,且腔体壁是刚性的,辐射波只能经由管口传出,这与无限大刚性障板上圆形活塞的辐射有一定的类似性,因此可以直接利用活塞的辐射阻抗对所求得的声阻抗率进行修正。已知无限大刚性障板上活塞的辐射声阻抗率的实部和虚部[19]分别为 在这里,r1是活塞的半径,R1和X1分别是活塞的阻函数和抗函数,如果令x=2kr1,则它们的具体形式为 在原来声阻抗率虚部的基础上增添一项辐射声阻抗虚部就能得到镶嵌聚氨酯泡沫共鸣器的修正声阻抗率虚部,进而得到修正后的共振频率。然后将修正后的理论模型与有限元软件仿真结果进行对比验证。 为了与理论模型对应起来,本文在运用有限元软件建模仿真时同样也使用了归一化参数,即所有材料的声速量和密度量均以水为参考进行归一化,而所有的结构长度量都以腔体半径作为参考,具体使用到的参数见表4。因为聚氨酯泡沫半径a是本文的设计变量,故没有在表4中给出具体的参数归一化结果。 表4 镶嵌聚氨酯泡沫共鸣器模型归一化参数Table 4 Normalized parameters of the resonator embedded with polyurethane foam in simulations 为了更加充分地进行模型验证,根据表4的参数,再令聚氨酯泡沫半径a分别为0.0001、0.05、0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.47 来构造不同的镶嵌聚氨酯泡沫共鸣器,通过有限元软件建模仿真,计算其共振频率以及对应的声场分布情况。 图6是镶嵌聚氨酯泡沫共鸣器(a=0.45)归一化模型在共振频率0.11578−0.0063008j 下的声场图与振型图,其声压和振动位移也分别用最大值进行了归一化处理,图例颜色越深代表相对幅值越大。其中0.11578−0.0063008j 的实部表示的是共振频率的大小,虚部表示结构的声波辐射能力,当虚部很小时可认为不具备传播性。图6(a)表示镶嵌聚氨酯泡沫共鸣器在共振频率下的归一化声压分布,显然开口处的声压呈向外辐射状态,证明了本文在做理论模型分析时考虑声辐射并用辐射阻抗对共振频率进行修正的做法是合理且必要的。同时,高声压值主要集中于聚氨酯泡沫弹性棒的顶端,由弹性棒的圆心向四周逐渐减小,说明此时发生的确实是聚氨酯泡沫弹性棒的轴向共振。而图6(b)是模型在该共振频率下的归一化振动位移状态,以纵振动模式进行振动,顶端振动幅度最大,证明了聚氨酯泡沫弹性棒确实能够通过其纵振动降低共鸣器的共振频率。 图6 归一化的声压与总位移(a=0.45) (共振频率为0.11578−0.0063008j)Fig.6 Normalized pressure distribution and total displacement at the complex frequency 0.11578−0.0063008j for a=0.45 图7是镶嵌聚氨酯泡沫共鸣器拥有不同半径聚氨酯泡沫时的品质因素。品质因素越小,共振频带越宽,而共鸣器共振频率的降低往往是以牺牲共振带宽为代价的。但是从图7来看,共鸣器嵌入聚氨酯泡沫并没有使品质因素产生大幅度的变化,且数值基本维持在10 以下。这意味着本文所设计的镶嵌聚氨酯泡沫共鸣器在实现低共振频率的同时依然拥有令人满意的共振带宽。 图7 镶嵌聚氨酯泡沫共鸣器的品质因素Fig.7 Quality factors of the resonator embedded with polyurethane foam 图8则是镶嵌聚氨酯泡沫共鸣器拥有不同半径的聚氨酯泡沫时的归一化共振频率。带圈、带星、带菱形的3 条曲线分别对应了未修正的理论模型、辐射修正后的理论模型以及通过有限元软件仿真的模型计算得到的共振频率。当聚氨酯泡沫半径接近0 也就是共鸣器没有嵌入聚氨酯泡沫的时候,三者计算得到的共振频率依次大约为0.5、0.323、0.318,与考虑了辐射修正的镶嵌聚氨酯泡沫共鸣器相比,产生差别的原因是前者没有考虑辐射阻抗,而后者钢壁参与了振动。当嵌入聚氨酯泡沫以后,没有经过修正的模型获得的共振频率始终为0.323,而考虑了辐射修正的理论模型与有限元软件仿真模型计算的结果基本一致,且随着聚氨酯泡沫半径的增加而呈现降低趋势,当聚氨酯泡沫半径增加至0.45时,二者的共振频率分别降低至0.113和0.116,与空共鸣器相比,频率降低至1/3。但是不可否认,二者确实还存在着一定的差异,这可以从两个方面进行解释。 图8 镶嵌聚氨酯泡沫共鸣器模型与有限元仿真模型的共振频率对比Fig.8 Resonant frequencies of the resonator embedded with polyurethane foam obtained by the theoretical model and the finite element simulation 一方面,无限大刚性障板上圆形活塞的辐射阻抗不能完全替代镶嵌聚氨酯泡沫共鸣器的真实辐射阻抗。本文用来对共振频率进行修正的辐射阻抗公式是建立在活塞表面振速为均匀分布的假设下的,而从有限元软件仿真出来的结果看,开口处的声压并非均匀分布,所以质点振速也就不可能满足均匀分布的条件,导致其实质上与活塞辐射没有严格等价。而开口处振速不均匀最本质的原因是聚氨酯泡沫和水各自在开口处的声阻抗不同。再加上共鸣器的腔体浅,水中的共振基频又高,因此在做有限元仿真时共鸣器腔体内的水可能包含了非平面波模态,而本文的理论模型只考虑了平面波模态。 另一方面,钢壁没有满足理论上严格意义的绝对刚要求,在水中会产生轻微振动,这点可以从图6(b)的振型图看出来。考虑到现实中人们对水下物体很难做到彻底隔振[20],因此在误差影响允许的范围之内,依然认为二者是对应一致的,也就是本文建立的镶嵌聚氨酯泡沫共鸣器的理论模型是有效的。 本文设计了一种镶嵌聚氨酯泡沫共鸣器,应用近似解析法求解腔体内声场建立了理论模型,获得了镶嵌聚氨酯泡沫共鸣器的声阻抗率以及共振频率的理论表达式。通过与一端封闭的有限长直管结构以及棒纵振动的声阻抗率对比,证明了理论模型的正确性。在此基础上,建立集中参数系统,分析镶嵌聚氨酯泡沫共鸣器共振频率降低的原因,一是聚氨酯泡沫弹性体的嵌入,使得共振结构的一阶共振频率变成了弹性棒的共振基频;二是聚氨酯泡沫弹性体的存在增加了共鸣腔的声容。利用有限元软件建模仿真,与经过辐射修正的理论模型进行对比,两者的共振频率相差不大,进一步体现理论模型的正确性,也说明镶嵌聚氨酯泡沫共鸣器在维持大开口共鸣器品质因素小、共振频带宽优势的同时实现了共振频率的降低,为设计新型水下低频声学共振结构提出了一种新的思路。

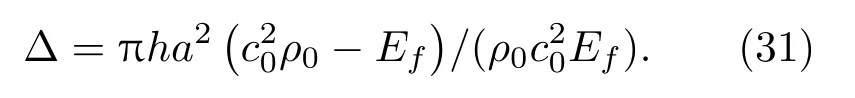
3 模型仿真研究
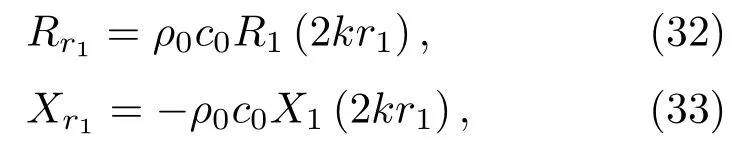
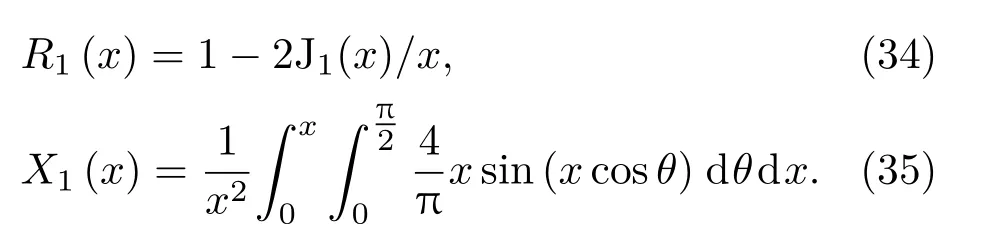


4 结论

