基于变分贝叶斯的分布式融合目标跟踪
胡振涛,杨诗博,胡玉梅,周 林,,金 勇,杨琳琳
(1.河南大学人工智能学院,河南郑州 450046;2.西北工业大学自动化学院,陕西西安 710129)
1 引言
目标跟踪技术被广泛地应用于协同定位、态势评估、视频监控、智能交通、海洋探测等各个领域[1].近年来,伴随着实际目标跟踪场景中探测空间范围扩大、探测干扰因素增多等复杂情况不断地出现,已有目标跟踪算法性能难以满足实际工程问题需求.由于状态估计器设计的优劣直接决定着目标跟踪效果的好坏,其研究近年来也因此受到国内外相关领域专家和学者的广泛关注[2].考虑到在实际目标跟踪系统中单个传感器量测精度往往难以达到系统滤波要求,设计依据数据融合机理的多传感器跟踪系统能够较好地解决单传感器跟踪系统滤波精度不足问题[3].分布式融合即上述思想的一种典型实现方式,它将各传感器量测送入局部滤波器分别进行状态估计,并将局部状态估计结果送入融合中心进行处理,从而获得相对于利用单传感器量测数据更好的目标状态估计效果,并且该方式具有计算量较小和容错率高的优点[4].文献[5]提出了一种用于分布式传感器网络的一致性容积卡尔曼滤波器;文献[6]提出了一类用于分布式传感器网络的一致性信息滤波器.上述滤波器都采用一致性方法处理各节点的目标状态估计,进而得到跟踪系统关于目标的状态最优估计.一致性方法能够在传感器节点数量较多的分布式传感器网络中取得较好的跟踪效果,但在传感器数量较少的分布式融合目标跟踪系统中具有精度较低和计算量较大等缺点.相比一致性方法,协方差交叉(Covariance Intersection,CI)融合策略能够实现信息的反馈调节,即将融合中心获取目标状态融合估计值后反馈于各局部滤波器,具有更高的稳定性,适合于传感器数量较少的分布式融合目标跟踪系统[7].此外,考虑到天气、温湿度等环境因素的影响,系统过程噪声时变且其统计量等先验信息未知因素,以及外界干扰、传感器硬件故障等原因造成量测出现随机异常值等情况,若仍在传统高斯假设下直接使用上述错误的噪声统计量和异常量测值等信息估计系统状态,则不可避免地导致融合估计结果变差,甚至引起滤波器发散现象[8].
为解决过程噪声时变且其统计量等先验信息未知的问题,文献[9]提出了一种基于变分贝叶斯(Variational Bayes,VB)方法的自适应线性卡尔曼滤波器,利用Inverse-Wishart(IW)分布作为状态一步预测协方差矩阵的先验分布,通过定点迭代方法更新系统状态和噪声参数的近似后验分布,自适应地估计系统状态和噪声.针对量测噪声时变未知问题,文献[8]首次在变分贝叶斯框架下结合Inverse-Gamma 分布实现状态空间模型系统中量测噪声分布参数和系统状态的联合估计,并在此基础上将其推广应用至非线性系统噪声未知问题[10].另外,考虑量测噪声异常值出现以及环境越来越复杂等导致的量测噪声具有非高斯重尾特性,造成传统滤波器的估计性能变差的具体情况[11].利用Student’s t 分布和Skew-t 分布等对量测异常值具有很好鲁棒性[12],文献[13]针对线性系统出现的重尾系统噪声和量测噪声,利用Student’s t分布对状态预测和量测似然概率密度函数建模,通过变分迭代更新目标状态和系统噪声参数的后验分布.随后在文献[14]中提出了一种基于Gaussian-Student’s t 分布混合的线性滤波器,通过自适应调节两种分布的混合参数实现线性系统的鲁棒估计.文献[6]针对分布式传感器网络提出了非线性一致性信息滤波器,分别采用Student’s t分布和IW 分布对过程噪声和量测噪声建模,并采用高斯近似(Gaussian Approximation,GA)的方法对非线性后验分布进行近似,但是高斯近似方法需要对多个分布进行加权拟合,特别是在传感器网络节点较多的情况下易导致计算复杂度的急剧增加.针对具有系统非线性、过程噪声时变以及量测噪声异常等特性的多传感器目标跟踪系统的状态估计与融合问题,本文提出一种基于变分贝叶斯的分布式融合无迹卡尔曼鲁棒滤波(Distributed Fusion Unscented Kalman Filter Based on Variational Bayes,DFUKF-VB)算法.
2 问题描述
考虑如下多传感器非线性离散时间动态系统,其状态空间模型与量测模型如下:
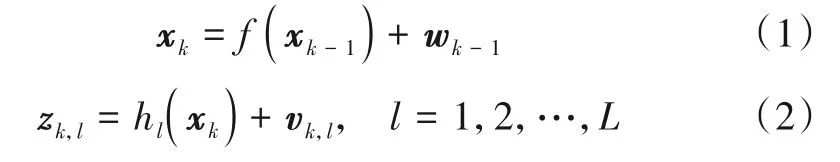
k表示离散时刻,xk为k时刻系统的状态向量,zk,l为k时刻第l个传感器的量测向量,f(·)表示状态转移方程,hl(·)表示第l个传感器的非线性量测方程;wk为零均值时变的过程噪声,其真实协方差矩阵Qk未知且时变;vk,l为第l个传感器具有随机异常值的量测噪声,其期望协方差矩阵为Rk,l;假设初始状态x0和任意时刻wk与vk,l均互不相关.
针对上述多传感器非线性系统状态估计问题,选用无迹卡尔曼滤波(Unscented Kalman Filter,UKF)来处理系统非线性估计问题,不同于扩展卡尔曼滤波算法(Extended Kalman Filter,EKF)[15],UKF 通过无迹变换处理均值和协方差矩阵的非线性传递,避免对非线性方程进行线性化处理,具有更高的估计精度[16];接下来,每一个局部平台选取UKF 滤波框架,结合VB 方法处理时变过程噪声和异常量测噪声,进而求得局部状态估计值;最后,利用分布式融合架构在融合中心对每一个局部状态估计值进行融合处理得到最终目标状态估计结果,并反馈其结果给各局部平台.算法实现结构如图1所示.
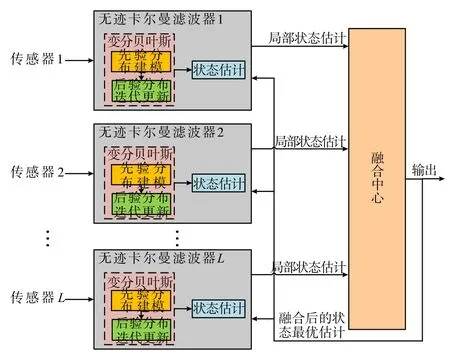
图1 DFUKF-VB算法结构图
3 状态预测协方差矩阵和量测似然建模
3.1 状态预测及其协方差矩阵的先验建模
对式(1)和式(2)描述的多传感器非线性系统,假设局部滤波器状态一步预测概率密度函数服从高斯分布:
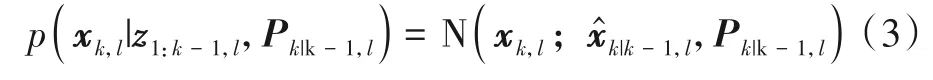
N(·;μ,Σ)表示均值为μ,方差为Σ的高斯分布.分别表示k时刻第l个局部滤波器的状态一步预测以及对应的协方差矩阵.基于UKF 滤波框架计算,考虑到过程噪声协方差矩阵Qk未知且时变,因此需要求Pk|k-1,l后验概率分布,而选取合适的共轭先验分布可以保证后验分布与先验分布具有相同的函数形式.这里选择IW 分布作为Pk|k-1,l的共轭先验分布,服从IW 分布的n×n维随机对称正定矩阵A的概率密度函数可表示为
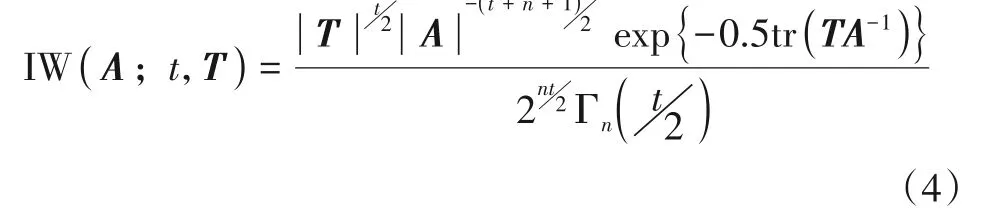
t为自由度参数,T为n×n维逆尺度矩阵,tr(·)表示矩阵的迹,Γn(·)表示一个n维的Gamma 函数.状态一步预测协方差矩阵的先验分布可表示为

将式(7)代入式(6)得到
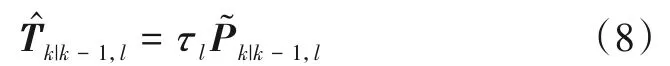
其中,τl≥0 为调谐参数和τl的选取依据实际应用场景而定.综上所述,由式(3)和式(5)可以求解状态预测及其协方差矩阵的先验分布,由式(7)和式(8)可求解状态预测协方差矩阵的IW先验分布参数.
3.2 量测似然建模
考虑到在式(2)描述的量测方程中量测噪声具有随机异常值,呈现出非高斯重尾特性,选取Student’s t分布对各传感器的量测噪声建模:
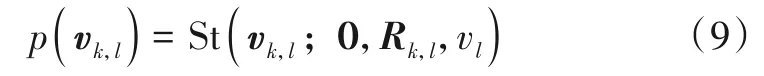
St(vk,l;0,Rk,l,vl)表示均值为0,尺度矩阵为Rk,l,自由度参数为vl的Student’s t分布.由于在分布式融合目标跟踪系统中各局部滤波器相互独立地对目标状态进行估计,所以在第l个局部滤波器中,量测似然概率密度函数满足p(zk,l|xk)≈p(zk,l|xk,l),结合式(2)和式(9),k时刻第l个局部滤波器的量测似然概率密度函数表示为
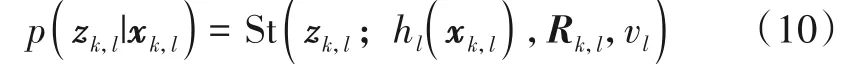
为处理Student’s t 分布的概率密度函数的闭合解难以求解问题,引入辅助随机变量λk,l,量测似然概率密度函数可写为如下积分形式:

G(·;α,β)表示Gamma分布的概率密度函数,α和β分别为形状参数和逆尺度参数.根据式(11),条件量测似然概率密度函数p(zk,l|xk,l,λk,l)最终可表示为如下形式:
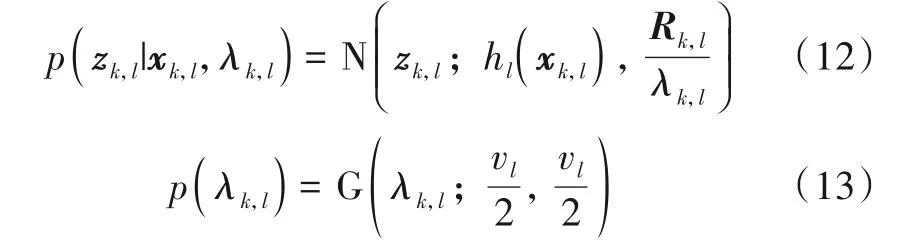
综上所述,由式(12)和式(13)可以得到量测似然概率密度函数.
4 待估计变量的后验分布迭代更新
4.1 联合后验概率密度函数的变分近似
为在各局部滤波器中估计系统状态和噪声参数,需要求解状态和噪声参数的联合后验概率密度函数p(xk,l,Pk|k-1,l,λk,l|z1:k,l).由于联合后验概率密度函数形式十分复杂,并且无法直接求得其解析解,因此论文采用平均场VB 近似的方法实现联合后验概率密度函数的近似解耦:
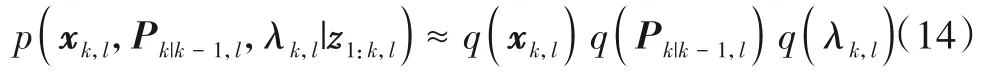
q(·)是后验概率密度函数p(·)的近似分布.于是求解联合后验概率密度函数问题就转化为寻找待估计变量的近似后验概率密度函数q(xk,l)q(Pk|k-1,l)q(λk,l).
根据VB近似思想,通过最小化q(xk,l)q(Pk|k-1,l)q(λk,l)与p(xk,l,Pk|k-1,l,λk,l|z1:k,l)之间的Kullback-Leibler 散度(Kullback-Leibler Divergence,KLD)来寻找后验概率密度函数的最优近似:
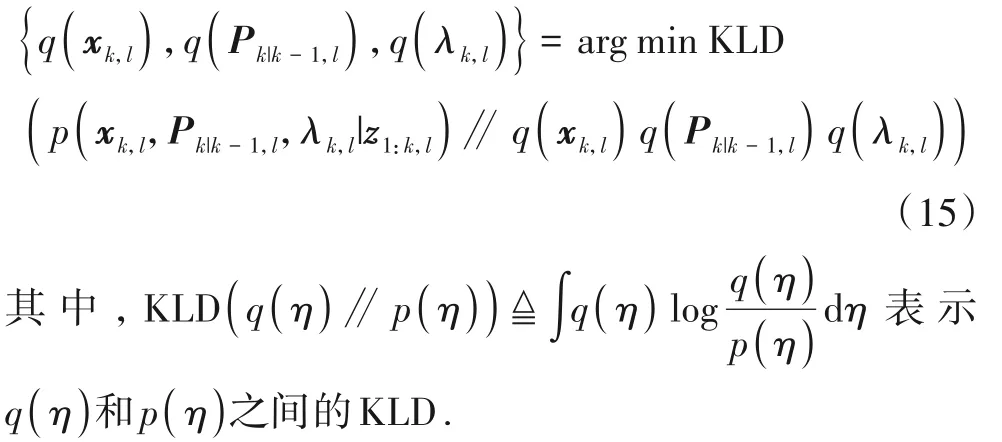
依据VB准则,式(15)最优近似解满足如下方程[8]:
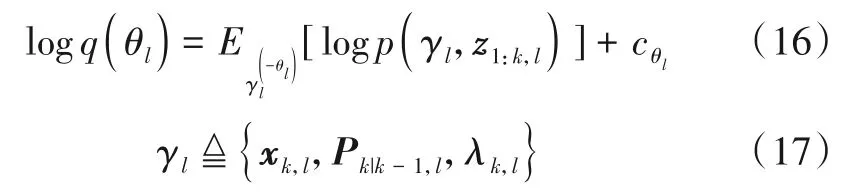
γl表示第l个局部滤波器待估计的变量集合,E[·]表示对括号内的函数或变量求期望,log(·)表示对括号内的函数或变量求对数,θl表示集合γl中的任意一个元素表示除θl外,集合γl中所有元素表示与θl有关的常数项.
4.2 状态和噪声参数的后验分布迭代更新
根据式(16),利用定点迭代方法逐个更新待估计变量的近似后验分布.根据状态空间模型的条件独立性,第l个局部滤波器变量的联合概率密度函数p(γl,z1:k,l)表示为
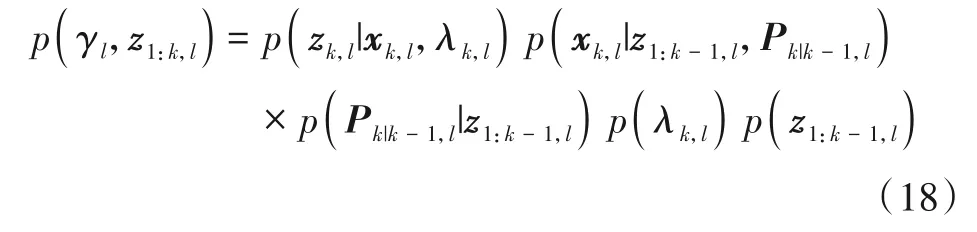
将式(3)、式(5)、式(12)、式(13)和式(18)代入式(16)对各待估计变量进行迭代更新.更新步骤如下:
令θl=Pk|k-1,l,将θl和式(18)代入式(16),更新为IW分布:


5 分布式状态估计的协方差交叉融合
对应于图1 中的融合中心模块,基于CI 融合准则对各局部滤波器的目标状态估计进行融合处理,并将融合结果反馈给局部滤波器.其步骤如下:
首先,融合中心接收到各局部滤波器的状态估计结果后,按照CI融合准则计算得到状态估计结果
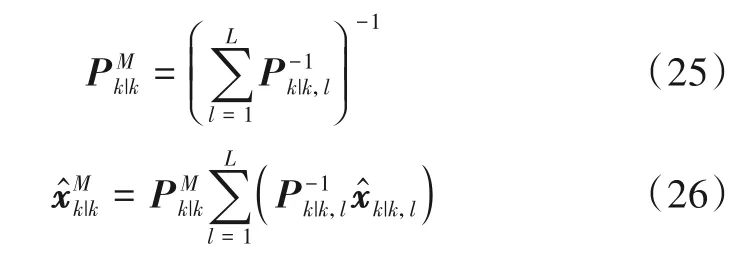
式中:v是清洁机器人的直线行走速度;n是履带驱动轮的转速;r是履带驱动轮的半径;n电是驱动电动机的转速;i是减速齿轮箱的减速比。
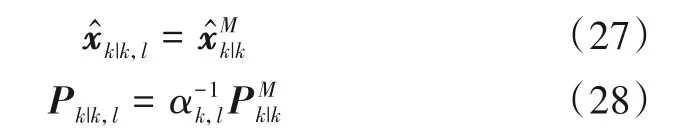
αk,l为反馈权重系数,它们随着局部状态估计协方差矩阵的变化而变化,且满足:

其中,‖ · ‖F表示Frobenius范数.
6 DFUKF-VB算法实现
综合本文第3 节到第5 节的内容,DFUKF-VB 算法实现步骤见算法1.

7 仿真结果与分析
仿真实验场景设定为典型二维平面目标跟踪,并与基于变分贝叶斯一致性无迹卡尔曼滤波器(Consistent Unscented Kalman Filter based on Variational Bayes,CUKF-VB)[6],基于变分贝叶斯无迹卡尔曼滤波器(Unscented Kalman Filter based on Variational Bayes,UKF-VB)[13],基于变分贝叶斯分布式融合扩展卡尔曼滤波器(Distributed Fusion Extended Kalman Filter based on Variational Bayes,DFEKF-VB)[15],具有固定不变提议过程噪声和量测噪声的分布式融合无迹卡尔曼滤波器(Distributed Fusion Unscented Kalman Filter based on Fixed Noise,DFUKF-FN)以及具有正确噪声统计信息的分布式融合无迹卡尔曼滤波器(Distributed Fusion Unscented Kalman Filter based on True Noise,DFUKF-TN)等5 种滤波方法结果进行比较,通过对比多个指标来验证本文提出算法相较于现有方法的可行性与有效性.值得注意的是,由于DFUKF-TN 使用了正确的噪声统计信息,所以它的滤波结果是最好的,将它看作标准参考算法,这里认为性能更接近于该滤波器性能的滤波器是一个更好的滤波器.算法仿真实验采用MATLAB R2018a 软件,计算机核心硬件具体配置:CPU Intel(R)Core(TM)i5-5200U,4 核,主频3.20 GHz,最大睿频2.7 GHz,8 GB内存.
7.1 仿真模型和参数
假设目标在二维水平面内做转弯率未知且恒定的转弯运动,目标的动力学模型表示为

采用位于水平面内不同位置的三个雷达对目标进行量测,得到目标与雷达的距离rk,l和方位角θk,l

(xk,yk)表示目标在k时刻所在位置坐标,(xl,yl)表示第l个雷达所在位置坐标,仿真实验中三个雷达的位置选取为(0 m,0 m)、(500 m,0 m)以及(0 m,500 m).量测噪声vk,l具有随机异常值,且量测异常概率均为10%时,量测噪声异常值通过如下方法产生:

其中,Rk,l表示k时刻第l个传感器的期望量测噪声协方差矩阵,pro.0.9 表示有90%的概率不会出现异常量测噪声,pro.0.1表示有10%的概率会出现异常量测噪声.三个雷达具有不同大小的量测噪声,其量测噪声协方差矩阵Rk,l选取如下:
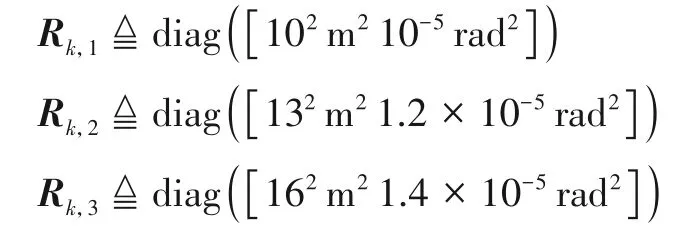
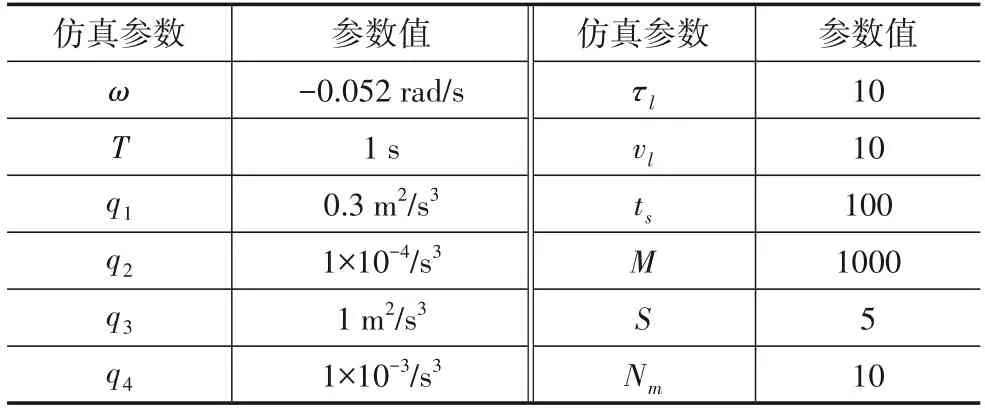
表1 仿真参数选取
7.2 评价指标

7.3 仿真结果和分析
图2 展示了单次仿真各滤波器目标跟踪轨迹.从图2 中可以看到DFUKF-FN 的跟踪轨迹多次较大幅度偏离真实轨迹,而UKF-VB、CUKF-VB、DFEKF-VB、DFUKF-TN 以及DFUKF-VB 跟踪轨迹未发生大幅度偏离真实轨迹的情况.这是由于DFUKF-FN 未使用Student’s t 分布对量测似然概率密度函数建模,因此该滤波器对随机出现的量测异常值十分敏感.而其他四种算法由于采用Student’s t 分布对量测似然概率密度函数建模,因此对随机出现的量测异常值具有鲁棒性.

图2 单次仿真各滤波器估计轨迹
图3给出了6种滤波算法对目标位置估计RMSE对比.由图3可以看出,在仿真时刻达到第20 s时,所有滤波器都能够稳定收敛.为了更直观地对比算法的精度,计算第20 s 到第100 s 时间内6 种滤波算法对目标位置估计的ARMSE,通过计算得到DFEKF-VB 相比DFUKF-VB高出49.59%,这是由于EKF只适用于弱非线性白噪声系统,造成DFEKF-VB 的滤波精度较低;UKF-VB 相比DFUKF-VB 高出18.60%,其原因在于DFUKF-VB采用CI融合策略对局部滤波器的状态估计进行了加权融合;CUKF-VB相比DFUKF-VB高出9.54%,说明相比于一致性算法,CI 融合结构更适于传感器数量较少的非线性目标跟踪系统.
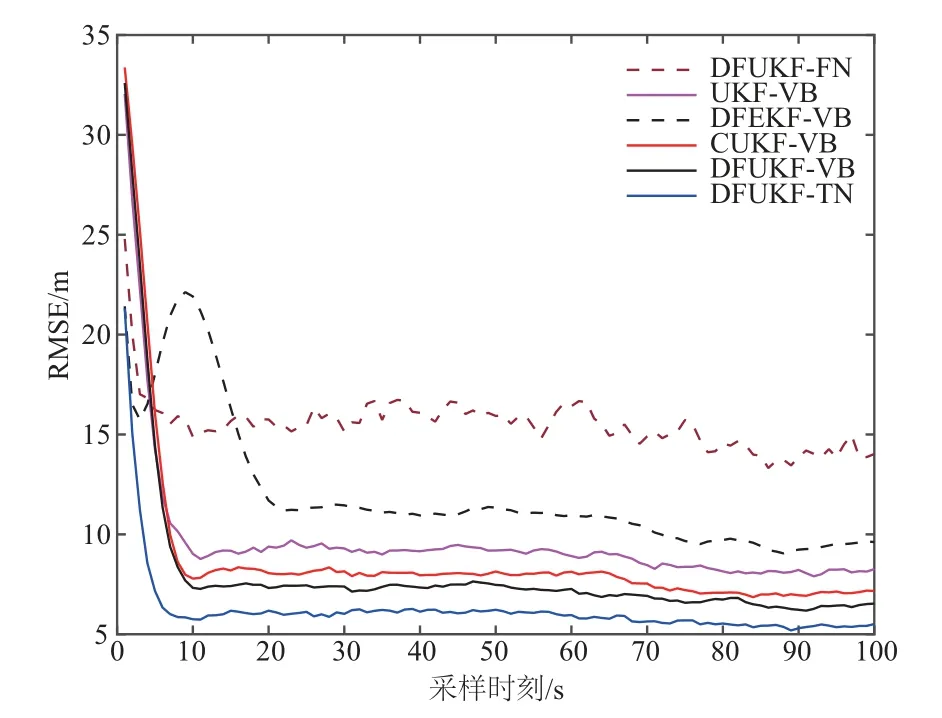
图3 位置估计RMSE
单次仿真条件下各滤波器的平均运行时长如表2所示.

表2 单次仿真条件下各滤波器的平均运行时长
由表2 可以看出,单次仿真条件下CUKF-VB 平均运行时长比DFUKF-VB 多56.07%,结合图3,说明在传感器数量较少的多传感器非线性目标跟踪系统中,DFUKF-VB的估计精度和计算实时性均优于CUKF-VB;DFUKF-VB 的平均运行时长比DFEKF-VB 和UKF-VB的平均运行时长分别多了37.81%和166.7%,结合图3可以得到,相较于DFEKF-VB和UKF-VB,DFUKF-VB虽然在计算复杂度有所增加,但其估计精度明显优于前两种算法.图4 展示了不同VB 迭代次数下各滤波器对目标位置估计的ARMSE 变化情况.从图4 中可以看出当VB 迭代次数Nm达到6 时,所有的滤波器都能够稳定收敛,可以根据这个结果来选择合适的变分迭代次数,从而节省算法运行时间.在目标位置估计的ARMSE 曲线稳定收敛之后,相同VB迭代次数情况下,DFUKF-VB对目标位置估计的ARMSE 更接近于DFUKF-TN,说明DFUKF-VB 估计精度优于除了理想DFUKF-TN 以外的其他4种滤波算法.为了使对比结果更具有说服力,计算图4 中Nm取6 到20 到之间所有滤波器对目标位置估计的ARMSE平均值,通过计算得到DFEKF-VB、UKF-VB以及CUKF-VB 相比DFUKF-VB 分别高出39.85%,13.04%和10.15%.

图4 不同变分迭代次数下位置估计ARMSE
图5 给出了不同调谐参数下本文提出滤波器和CUKF-VB对目标位置估计的RMSE对比图.从图5中可以看出,当τl取值变化时,DFUKF-VB对目标位置估计的RMSE 在第20 s 时均能够稳定收敛,说明其具有较高的自适应性,在调谐参数变化时仍能快速稳定收敛.计算图5 中第20 s 到第100 s 时间内两个滤波器对目标位置估计的ARMSE,通过计算得到:当τl取10,15,25 和50时,CUKF-VB 相比DFUKF-VB 分别分别高出9.54%,10.16%,10.41%和10.65%.
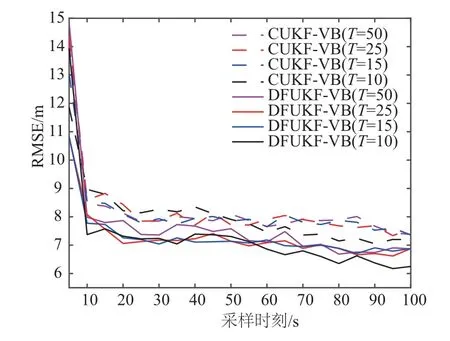
图5 不同调谐参数下位置估计RMSE
图6给出传感器量测异常概率p对DFUKF-VB位置估计的RMSE影响.由图中结果可看出当传感器量测异常概率从0%增加到20%时,RMSE变化不明显,其原因在于采用Student’s t 分布对量测似然概率密度函数建模,有效改善了量测异常对状态估计精度不利影响;但当传感器量测异常概率逐渐增加到30%时,RMSE增加明显增加,这是因为量测异常值出现的更频繁,尤其当量测异常值连续出现时,将对滤波器造成较大的影响.
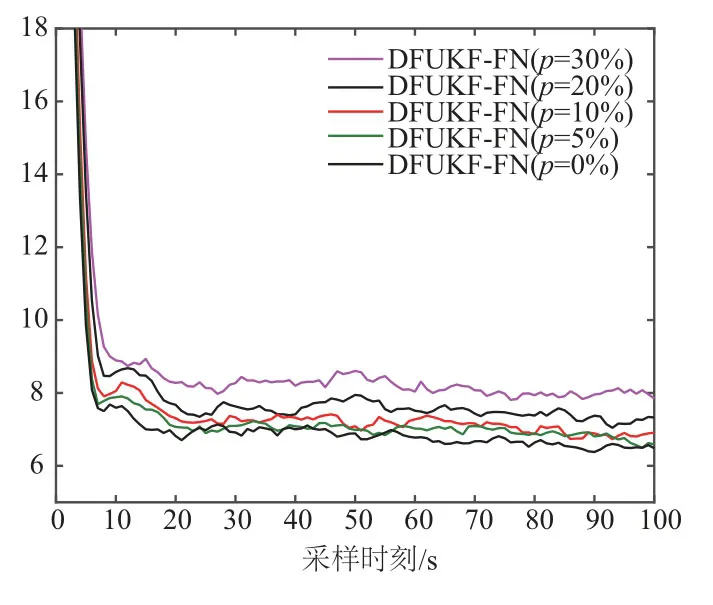
图6 不同异常概率位置估计RMSE
8 结论
本文提出了一种基于变分贝叶斯的分布式融合目标跟踪算法.与传统的分布式滤波算法相比,具有以下特点:首先,引入反馈式CI 融合策略,利用多传感器量测分别实现局部滤波器的状态估计,进而利用CI 融合方式得到状态估计值,并将其反馈于所有局部滤波器,实现对局部滤波结果的优化.有效解决因单传感器量测估计精度不足的问题,并且避免一致性算法的计算量大的问题.其次,在UKF 框架中引入VB 方法,采用参数化IW 分布作为状态预测协方差矩阵的共轭先验分布和Student’s t分布对量测似然概率密度函数建模,改善非线性系统估计中出现的过程噪声时变和量测噪声随机异常值的影响,并在VB 框架下实现了状态与噪声统计特性的联合估计.再有,针对相互耦合待估计变量的联合概率密度函数采用平均场VB 进行近似解耦,并对解耦后的各边缘变分分布参数采用定点迭代的方法进行更新,同时通过控制迭代次数平衡估计滤波精度和实时性.

