基于不确定性与错误分类率博弈的序贯三支决策模型
张清华,黄志康,高 满,艾志华
(重庆邮电大学计算智能重庆市重点实验室,重庆 400065)
1 引言
近年来,不确定性问题成为智能信息处理[1,2]的一个热点.其中,三支决策[3,4]将论域划分为三个不相交的区域,即正、负、边界域;针对不同的区域执行不同的策略.由于三支决策在信息不充分时无法对边界域对象执行具体的决策,Yao[5,6]在多粒度空间下提出了序贯三支决策模型.近年来关于序贯三支决策模型的研究已引起许多学者的广泛关注[7~9].在动态多尺度决策表中,Li[10]等借助序贯三支决策的思想应用到动态多尺度决策表中,用于求解最优尺度问题.此外,在推荐系统应用方面,Min[11]等将三支决策的思想引入到推荐系统中,提出基于回归的三支推荐模型;考虑到数据同时具有瞬时和动态的特征,Yang[12]等在三支近似背景下整合了动态性和模糊性用于研究模糊概率空间下的近似问题.更多关于序贯三支决策的研究进展可以参考文献[13~15].
然而,传统的序贯三支决策模型只对决策后的边界域进行了处理,对正、负区域不作处理,因此存在两类分类错误现象[16].为了减少两类分类错误发生的几率,文献[17]设计了一种惩罚函数对两类分类错误的相应代价参数进行惩罚.使得决策在由粗粒度到细粒度渐进的过程中误分类现象逐渐减少,最终提高了分类精度.进一步地,在文献[18]中,从粒子细分的角度提出了自主纠错的序贯三支决策模型.文中提出了基于聚类技术来寻找纠错对象的模型,进而得到每一粒层的纠错阈值.在序贯三支决策模型中,决策阈值的确定基于以下两种假设:
(1)每一粒层的决策阈值对相同,即(α1,β1)=(α2,β2)=…=(αn,βn);
(2)每一粒层的决策阈值对满足0 ≤β1≤β2≤…≤βn≤αn≤αn-1≤…≤α1≤1.
现有序贯三支决策模型的研究主要从提高模型的分类精度或减少分类过程中边界域的不确定性来求取决策阈值.这些研究能满足不同场景下的需求,且能取得一定的效果.然而,在实际决策中,如何综合两方面的因素来做出更合理的决策是值得研究的问题.例如,决策者希望分类过程中错误分类率小的同时边界域的不确定性也尽可能小.如此,既能保证一定的分类精度,也能获得较高的决策效率.而在序贯三支决策模型中,这两者很难同时达到最优,而是存在一种负相关变化关系.因此,如何平衡序贯三支决策过程中错误分类率与边界域不确定性两者之间的矛盾,进而选取出每一粒层自适应的决策阈值是一个值得研究的问题.博弈论作为一种对策论,最初以数学大师冯·诺依曼(John von Neumann)和经济学者摩根斯坦(Oskar Morgenstern)的巨著《博弈理论与经济行为》的出版为标志,已广泛应用于决策领域,并取得了良好的效果.为了解决上述问题,本文首先从理论方面分析了序贯三支决策过程中每一粒层错误分类率与不确定性之间的关系,并证明了两者呈现负相关变化关系;其次,结合博弈论的思想,构建了错误分类率与不确定性之间博弈的过程.随后,为了比较模型的效果,基于不确定性与错误分类率设计了多目标决策下的阈值求取方法.最后,在同等实验条件下,进行了两种模型的对比实验,实验结果验证了所提博弈论序贯三支决策模型的有效性和合理性.
2 相关基础
为了便于本文的阐述,本节对决策信息系统、等价关系、粗糙隶属度、信息增益、信息增益比、序贯三支决策、博弈论等一些基本概念进行了简要回顾.
定义1决策信息系统[19].给定一个决策信息系统S=(U,C∪D,V,f),其中,U={x1,x2,…,xn}是一个非空有限对象集,即论域.C={c1,c2,…,cm}和D={d}分别表示条件属性集和决策属性集且满足C∩D=∅.V是一个属性值集合,f:U×C→V是一个信息函数,映射一个具体对象到一个具体属性值.
定义2等价关系[19].给定一个决策信息系统S=(U,C∪D,V,f),对于属性子集B(B⊆C),则论域U上的一个等价关系ind(B)可被定义如下:
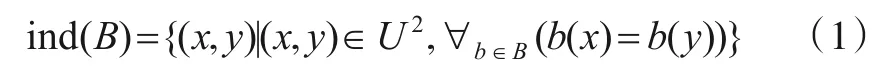
由等价关系ind(B)形成了论域U上的一个划分,记U/ind(B)={E|E⊆U∧∀x,y∈E,b∈B(b(x)=b(y))},[x]ind(B)∈U/ind(B)表示对象x在等价关系ind(B)上形成的等价类,简记为[x]B或[x].
定义3粗糙隶属度[20].给定一个决策信息系统S=(U,C∪D,V,f),X(X⊆U)表示目标子集,B(B⊆C)表示属性子集.对于∀x∈U,x的粗糙隶属度定义为:
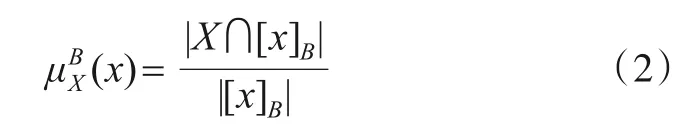
其中,|·|称为集合的势.为了后文叙述的方便,粗糙隶属度简记为Pr(X|[x]).
定义4信息增益[21].给定一个决策信息系统S=(U,C∪D,V,f).设论域U在等价关系ind(B)(B⊆C)和ind(D)下的划分分别为U/B={B1,B2,…,Bm}和U/D={D1,D2,…,Dn},则信息增益Gain(D,B)可定义为:
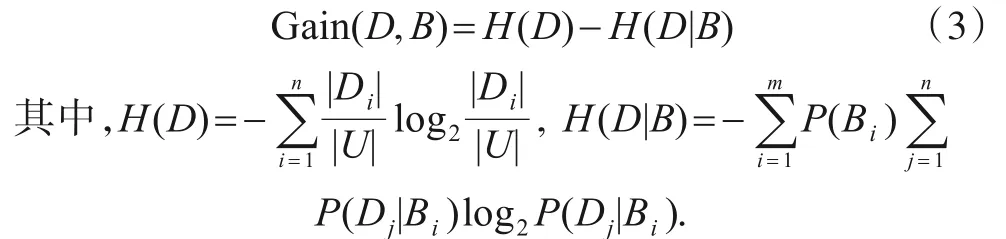
定义5信息增益比[22].给定一个决策信息系统S=(U,C∪D,V,f).条件属性集B(B⊆C)和决策属性集D对论域U形成的划分分别为U/B={B1,B2,…,Bm},U/D={D1,D2,…,Dn}.则信息增益比gR(D,B)可定义为其信息增益Gain(D,B)与划分U/B关于属性B的值的熵HB(U)之比,即

定义6序贯三支决策[5,6].给定一个决策信息系统S=(U,C∪D,V,f),C1⊆C2⊆…⊆Cn=C(|C|=n) 表 示一组连续的属性集,则序贯三支决策(Sequential Three-Way Decisions,STWD)可定义如下:
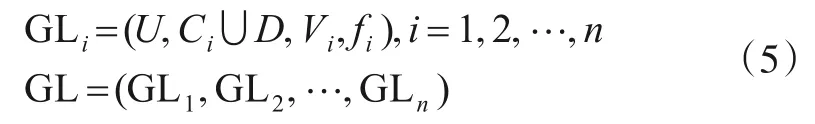
其中,GLi表示在等价关系U/Ci下的第i粒层,GL 表示一个层次的粒结构.
定义7博弈的规范式[23].设一个三元组G=[N,{Si},{Pi}]表示博弈的一个规范式,其中N表示游戏玩家的一个有限集合,即N={n1,n2,…,ni}.Si表示玩家ni采取的策略集,即Si={si1,si2,…,sij}.其中,j代表玩家ni执行的策略数目.Pi表示任意一个策略组合下带给玩家ni的收益.
3 序贯三支决策模型的错误分类率与不确定性关系分析
在文献[18]中,Zhang 等基于两类分类错误提出了自主纠错的机制,以期减少对象的错误分类率,所求每一粒层的纠错阈值在提高分类精度上取得了一定的效果.然而,纠错是需要额外成本的,当选取的纠错对象较多时,决策区域的错误分类率会降低,而边界域的不确定性会较大,同时决策效率会较低,反之亦然.为了直观的理解序贯三支决策模型每一粒层的错误分类率与不确定性的关系,下面给出了相关的定义.
定义8序贯三支决策模型的错误分类率[18].在粒 层GLi,给定一个目标集合X={x1,x2,…,xn},POSi(X),NEGi(X),BNDi(X)分别表示第i粒层的正、负、边界区域.则,正、负区域及总的错误分类率(Error Classification Rate,ECR)可分别表示如下:
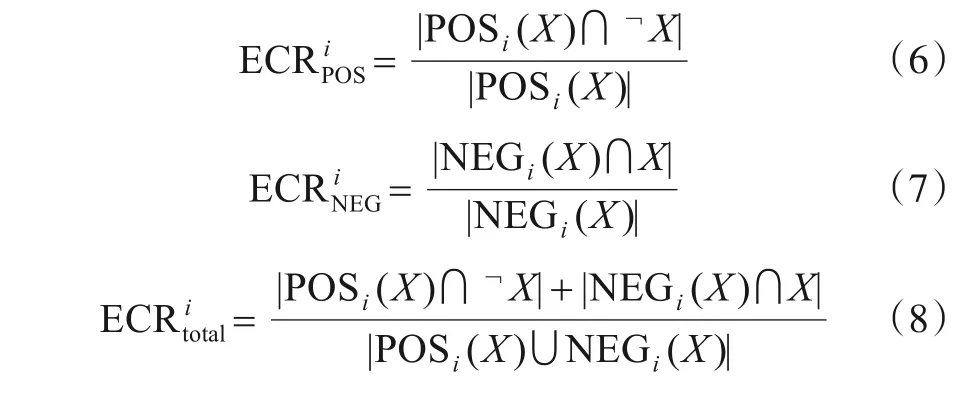
由以上定义可知,错误分类率ECR 主要表征了决策后,正、负区域错误分类的样本数与该区域总的样本数之比.式(6)~(8)既刻画了两类错误分类存在的现象,也能对决策给予一定错误容忍度.为了表征对于边界域待分类样本的不确定性,下面给出了梁吉业[24]等建立的模糊熵来度量边界域的不确定性.
定义9边界域的不确性[24].在第GLi粒层,给定目标子集X(X⊆U).设论域U的一个三支划分为f:U→{POSi(X),BNDi(X),NEGi(X)},则边界域BNDi(X)的不确定性可用如下的模糊熵来描述:
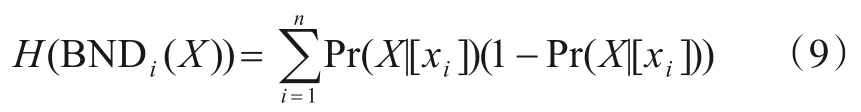
其中,xi∈BNDi(X)表示边界域中的对象.当等价类的隶属度从0 或1 趋近于0.5 时,边界域的不确定性逐渐增大,当隶属度取到0 或1 时不确定性达到最小,即模糊熵为0,反之亦然.
为了展示每一粒层正、负区域总的错误分类率与边界域不确定性之间的定性关系,给出了下面的相关定理.
定理1给定第i粒层GLi的一个决策信息系统Si=(Ui,Ci∪D,Vi,fi),X(X⊆U)是目标子集.对于一对决策阈值(α,β),0 ≤β≤α≤1.当α减小,β增大时将增大,H(BNDi(X))将减小.
证明任给一对决策阈值(α,β),满足0 ≤β≤α≤1.为了描述方便,不妨设β=1-α.假定ε(0 ≤ε≤1)表示隶属度的增量,并且有α↓=α-ε,β↑=β+ε.其中↑,↓分别表示增加和减少的标记,以下将从两方面给予证明:
(1)令集合POSi(X)={[xi]|Pr(X|[xi])≥α},NEGi(X)={[xi]|Pr(X|[xi])≤β},BNDi(X)={[xi]|β<Pr(X|[xi])<α}分别表示第i粒层的正区域、负区域、边界域.令Pr(X|[xj])≤β+ε}分别表示阈值变化后正区域、负区域的增量.令

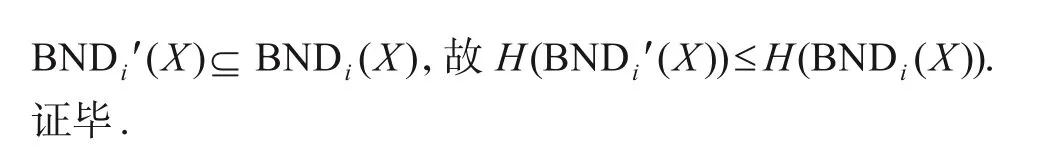
类似于定理1可得以下定理2:
定理2给定第i粒层GLi的一个决策信息系统Si=(Ui,Ci∪D,Vi,fi),X(X⊆U)是目标子集.对于决策阈值(α,β),0 ≤β≤α≤1,当α增大,β减小时,将减少,H(BNDi(X))将增大.
从定理1、2 中可以看到,决策正、负区域总的错误分类率与边界域的不确定性呈现负相关变化关系.
4 基于不确定性与错误分类率博弈的序贯三支决策模型
在第3 节中,分析了正、负区域错误分类率与边界域不确定性之间的关系.在本节中,引入博弈论的思想构造两个对象之间的博弈,在纯策略博弈下去搜寻两者的均衡点.具体为:在每一粒层中博弈的两个游戏玩家分别为错误分类率与不确定性,游戏的策略为阈值对(α,β)的变化.随着阈值对的动态变化,博弈双方的收益也会随之变化.博弈的相关要素包括博弈策略、收益函数及博弈的停止条件.
4.1 博弈策略及收益分析
纯策略纳什均衡通常用来表示可能的博弈结果.当游戏玩家选择的策略组成均衡后,就形成了一个平衡局势.一个策略组合(s1n,s2m)是纯策略纳什均衡,仅当s1n和s2m对于游戏参与者n1,n2来说是对对方最好的反馈.本文中的游戏玩家为决策正、负区域总的错误分类率和边界域的不确定性H(BNDi(X)),记为N={E,H}.在此基础上,纯策略纳什均衡可形式化的表述如下:
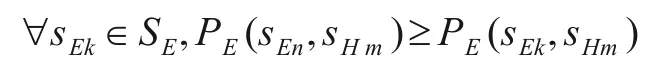
其中,sEn,sEk∈SE并且n≠k,sHm∈SH.
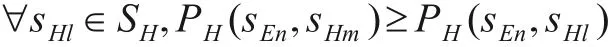
其中,sHm,sHl∈SH并且m≠l,sEn∈SE.
收益函数PΩ(sEn,sHm),Ω∈{E,H}表示相应玩家在执行当前策略下的收益.在本文的模型中,由于博弈的对象是错误分类率和不确定性,这两个玩家主体的收益不在同一维度和量纲下,无法进行直接的比较和计算.为了使两个不同标准的量纲具有可比性,本文使用了L-2[25]范数来消除错误分类率和不确定性的维度影响,通过数据标准化使得归一化后的两个量纲能用于计算总收益,归一化的公式如下:
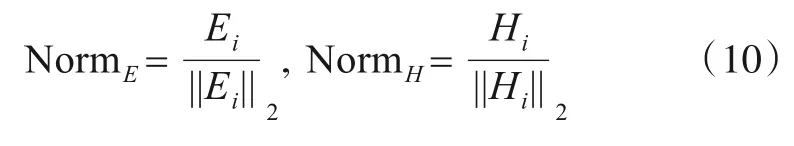
其 中,Ei=Hi=H(BNDi(X)).NormE,NormH分别表示归一化后的错误分类率和不确定性.
博弈的策略组合为S=SE×SH,其中SE={sE1,sE2,…,sEn}是E可能执行的策略集合,SH={sH1,sH2,…,sHm}是H可能执行的策略集合.n,m分别代表了E,H执行策略集的数目.在本文构建的博弈模型中,策略集对应于阈值α,β的变化.每个游戏玩家可选择两种策略中的一种,即提升阈值或降低阈值,记为A={↑,↓}.其中↑表示提升操作,↓表示降低操作.根据之前的分析可知,当阈值α选择提升动作时,即执行策略α→α↑时,正区域的错误分类率减少,不变,H(BNDi(X))增加;当阈值β选择降低动作时,即执行β→β↓时,负区域的错误分类率减少,不变,H(BNDi(X))增加;反之亦然.详细的变化趋势如表1所示.
表1 和H(BNDi(X))随阈值改变而变化的趋势

表1 和H(BNDi(X))随阈值改变而变化的趋势
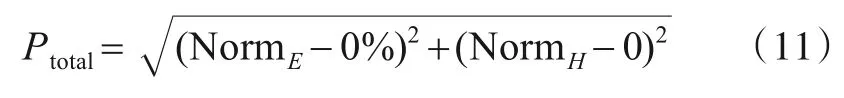
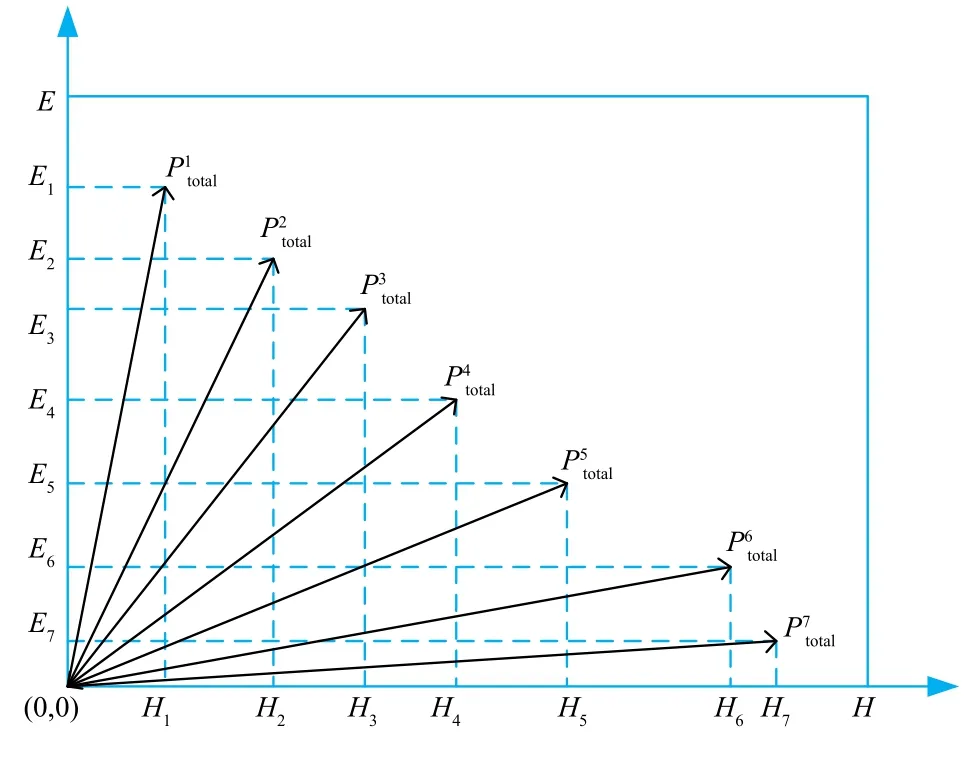
图1 不同策略下总收益示意图
综合上面的分析,为了寻找不确定性与错误分类率的平衡点,博弈策略的初始阈值(α,β)应满足0 ≤β≤α≤1.游戏玩家通过执行不同的策略来改变初始阈值,选取不同的初始阈值会影响玩家可能的执行策略.特别地,当初始阈值为β=0,α=1 时,意味着此时的策略拥有最小的错误分类率;当α=β=γ时,此时拥有最小的不确定性.对于本文的模型,在假设(α=1,β=0)的基础之上,α执行逐渐减小的策略,β执行逐渐增加的策略.设常量cE,cH分别表示E和H每次改变阈值的步长,且cE,cH满足0 <cE,cH≤1,则相应得到两个玩家的策略集分别为:
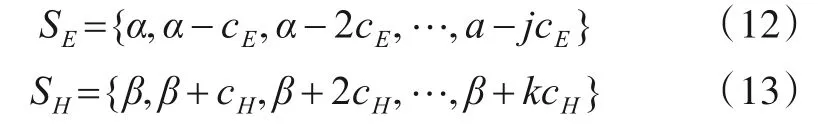
由此可以得到不同策略下游戏玩家的收益表如表2所示.
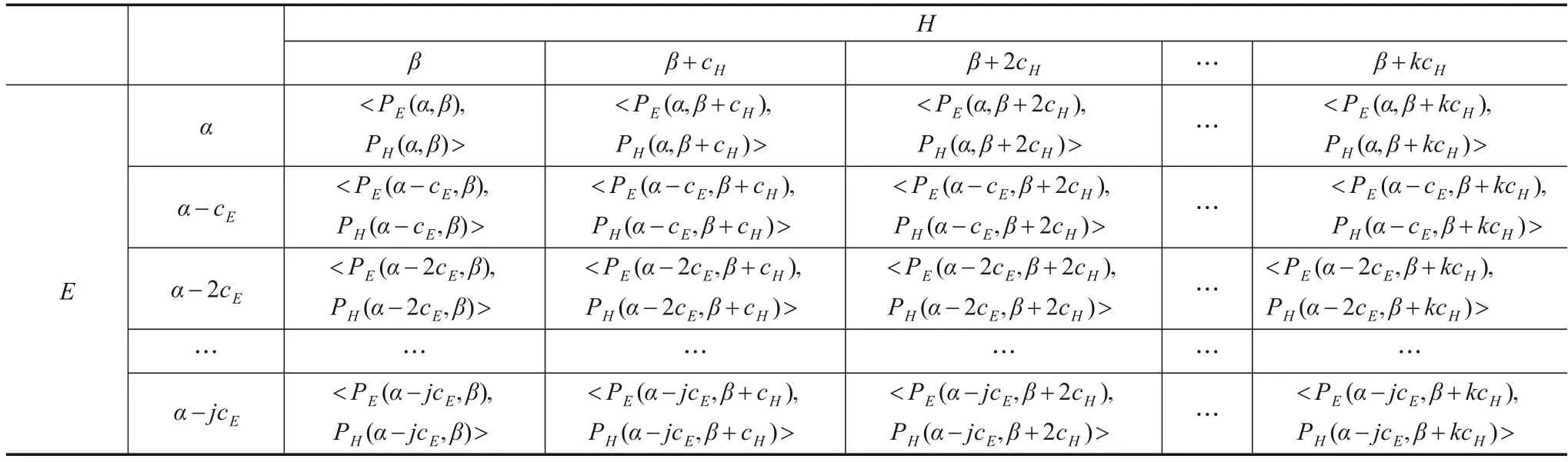
表2 不同策略组合下错误分类率与不确定性博弈的收益表
一般,k和j的值不是固定的,与cE和cH的大小有关.当选择的策略步长较大时具有较少的策略数目.反之亦然,同时收益矩阵也会更复杂,计算的复杂度也会线性增加.一般根据实际需要,选择合适的步长.在所提模型中,本文设定了cH=cE={0.01,0.05,0.1},因为本文的重心是想说明从这两个角度博弈的思想,而k,j选择的多少对本文的思想是没有影响的,因此,没有再详细讨论.
4.2 博弈重复及停止条件
4.2.1 博弈重复
设给定当前博弈的策略集为SE={sE1,sE2,…,sEn},SH={sH1,sH2,…,sHm}分别表示玩家E,H的策略集,初始阈值为(α,β).若策略(sEp,sHq)是当前局势下的均衡点,对应的阈值为(α*,β*).则后续博弈策略集的初始阈值更新为当前的阈值(α*,β*)且博弈双方的策略集和之前相同.即后续博弈重复的策略集仍然为SE={sE1,sE2,…,sEn},SH={sH1,sH2,…,sHm}.
4.2.2 博弈停止条件
在博弈重复中,设置博弈停止条件能让博弈重复一定次数在合适的时机停下来,此时得到的阈值即为最终的输出结果.博弈的停止条件根据具体需要可以设置不同的标准,包括但不限于:博弈的结果阈值(α,β)不再满足0 ≤β≤α≤1;当前均衡没有提高上一步初始阈值的收益;一方的收益弥补不了另一方的损失;双方都出现亏损.结合本文模型,设计了如下的博弈停止条件:
(1)给定初始策略集SE={sE1,sE2,…,sEn},SH={sH1,sH2,…,sHm}及初始阈值(α=1,β=0).E以常量cE来改变自己的策略,H以常量cH来改变自己的策略.记initial,current,previous,final 分别表示初始、当前、上一步、最终四种策略状态.若则更新初始阈值(α,β)→(α′,β′),其中α′=α-Δ,β′=β+Δ,同时以相同的策略重复步骤1.
为了更直观的阐述所提模型的思想,下面给出了模型的算法,如算法1所示.


5 对比实验及分析
本文从UCI 数据库中选取了10 个标准数据集Breast-Cancer-Wisconsin(BCW)、Mammographic-Masses(MM)、Pen-based Recognition of Handwritten(PRH)、Mushroom(M)、Wireless Indoor Localization(WIL)、Optical Recognition of Handwritten(ORH)、Website Phishing(WP)、Car Evaluation(CE)、Statlog(S)、Wholesale Customers(WC)进行了对比实验.并对数据集进行了预处理.所使用的实验环境为:Windows 10,Inte(lR)Core(TM)i7-7700 CPU @ 3.60 GHz,4 核,8 GB RAM,编程语言为Matlab 2016b.
在博弈的策略组合中,本文设定了一个步长集δ={0.01,0.05,0.1}.即,分别在步长为0.01、0.05、0.1 情况下进行了自对比实验;同时由于博弈论与多目标决策联系紧密但本质不同,为了比较两者的效果,本文在同等实验条件下设计了博弈论与多目标决策的对比实验.在多目标决策中,TOPSIS 方法是常用的基于多目标决策的评价函数,其主要思想是评价目标对象与理想解(最优解)和负理想解(最劣解)的贴近程度进行一个综合排序.在可行解中,若某一解距最优解越近(距离越小),同时距最劣解越远(距离越大),则此时的解为决策结果.基于以上的思想,本文设计了多目标决策方法下的理想解和负理想解如下.

其中min(Efea),min(Hfea),max(Efea),max(Hfea)分别表示集合Efea,Hfea的最小(最大)值.
根据式(14)、式(15)结合多目标决策的思想,本文从错误分类率与不确定性分别到理想解与负理想解的欧式距离(distEuclidean)设计了综合评价函数如下:
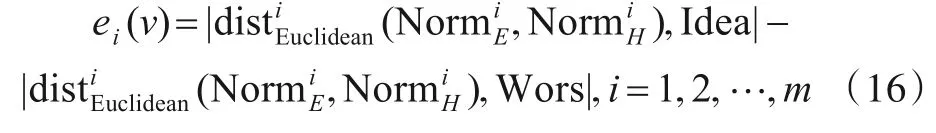
在实际决策中,决策者希望所求的解越接近理想解的同时越背离最劣解.为此,根据所得的综合评价函数,给出了如下多目标决策下的最优解求取办法:
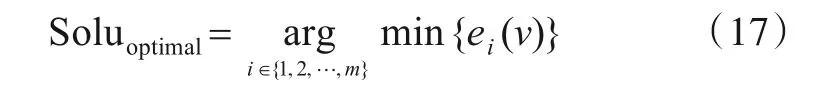
根据以上的实验方案,设计了两个模型的对比实验.由于文章的篇幅有限,10个数据集每一粒层阈值对的结果表没有在此一一陈列,且所有表的结论是一致的.因此,这里仅展示了有代表性数据集的实验结果,如表3~5、图2所示.
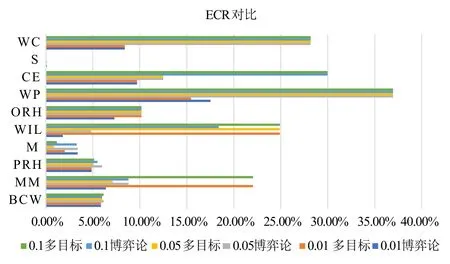
图2 10个数据集在不同步长下的ECR对比
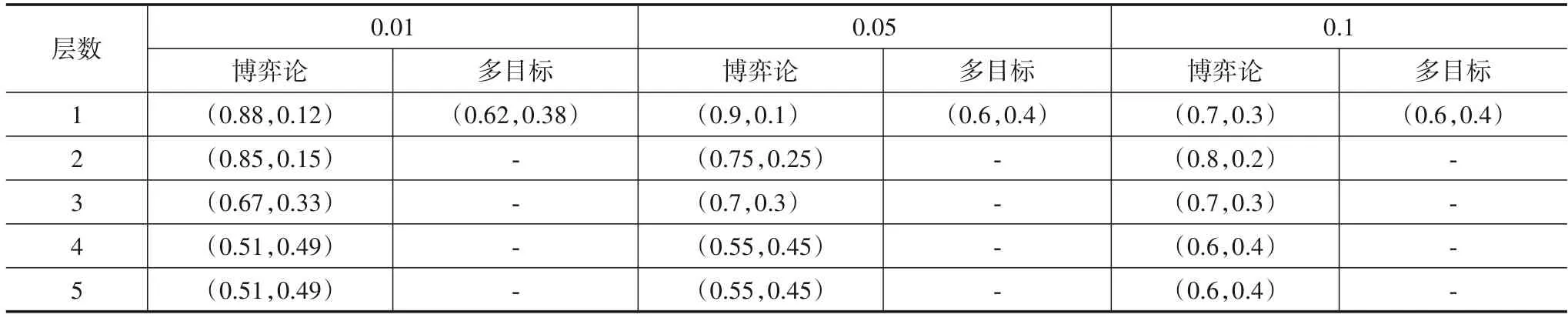
表3 WIL每一粒层的决策阈值对实验结果(α,β)
从算法1中可以看出,Step1、Step2首先得到每一粒层的决策信息表,同时计算出每个等价类的隶属度,这部分时间复杂度为O(nmk).其中,n代表对象的个数,m代表属性的个数,k代表等价类的个数;Step3 为初始化策略集,时间复杂度为O(1);Step4 为归一化及判断求取结果阈值的过程.因为博弈论找到均衡后算法就停止了,所以最坏的情形下是遍历完所有策略,此时时间复杂度为O(k).其中k为策略集数目.综上可知,本文模型的时间复杂度最差情况下为O(nmk).在多目标决策方法中,Step1~Step3 与博弈论算法的步骤是一样的,而在Step4 中,多目标决策方法通过遍历所有步骤来寻求最优解,这步的时间复杂度固定为O(k).综上,博弈论的模型具有更低的时间复杂度.
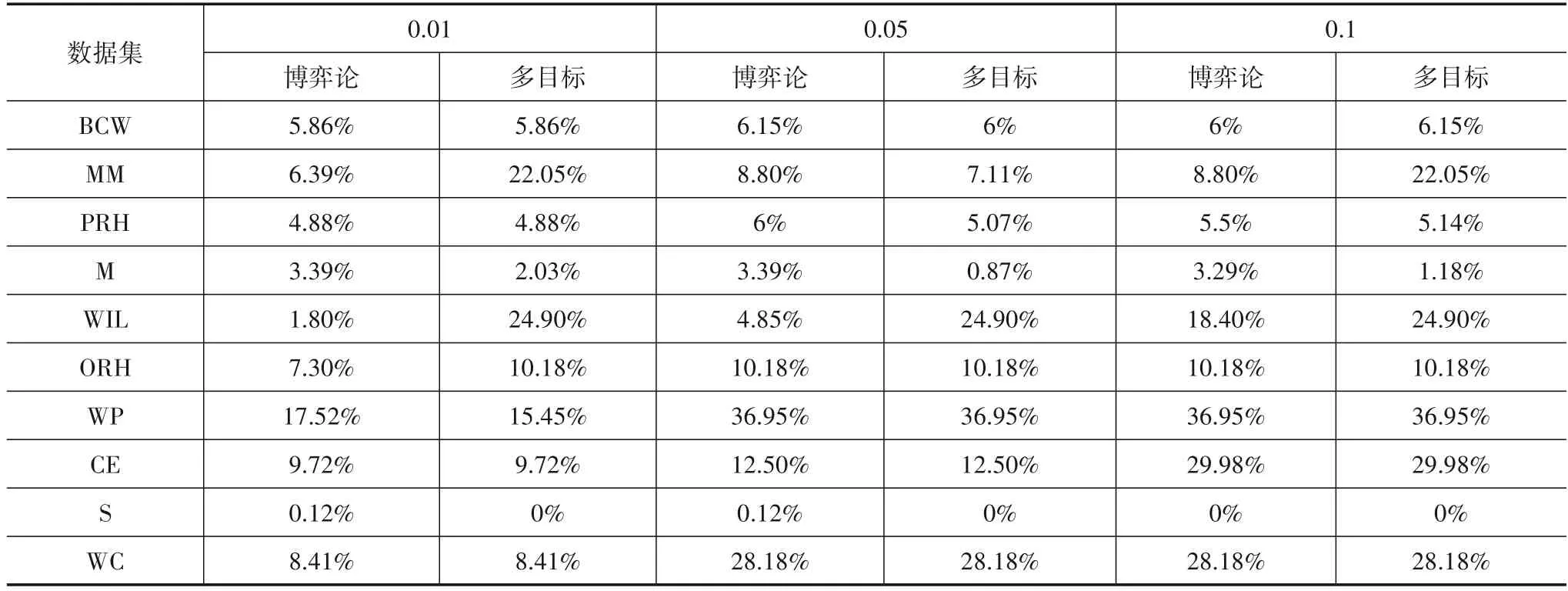
表4 不同数据集下的错误分类率
此外,为了更好的说明算法的时间开销差异,表5给出了博弈论的模型与多目标决策方法在同等实验条件下的运行时间对比分析.从表5 中可以看出,除个别数据集,如WIL,博弈论模型的时间开销略高于多目标决策;以及个别参数下,如BCW 数据集0.01 步长、MM数据集0.1 步长下稍微差一点,其他都优于多目标决策方法.
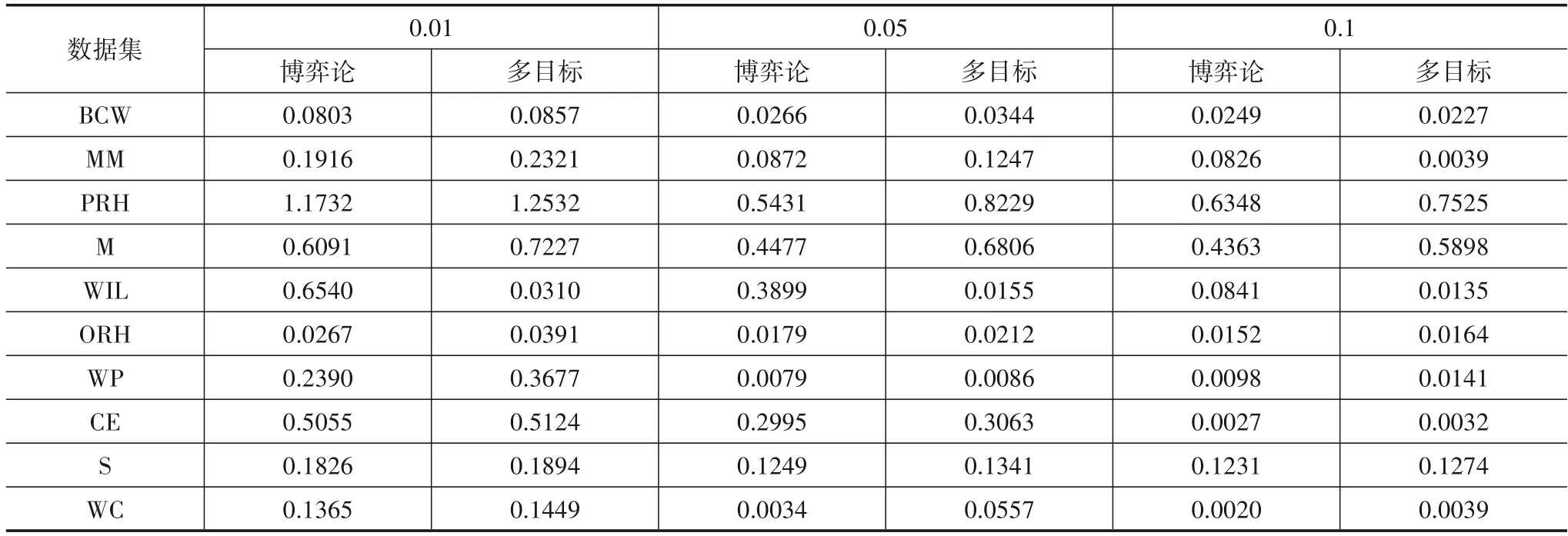
表5 不同数据集下运行时间对比(时间/s)
从图2中可以看到,在BCW数据集中.从横向对比来看,博弈的序贯三支决策模型随着步长的变小,决策后的错误分类率逐渐减少,也即分类精度逐渐提高.这是因为较小的步长意味着博弈的策略集更精细,这符合人类的认知规律.虽然博弈过程中搜索平衡阈值的时间开销变大了,但追求的分类精度更高了.另一方面,从博弈论模型与多目标决策方法的纵向对比来看,可以看出,相比博弈论的序贯三支决策模型,多目标决策方法在不同数据集同等步长下的错误分类率有时低,有时高.但在10 个数据集的总体情况下,多目标决策的模型相比博弈论的模型拥有更高错误分类率.此外,在表3中,博弈论模型具有更为合理的阈值对结构,即决策阈值对是逐渐向中间靠近,从而使得每一层的边界域逐渐减少.这是因为多目标决策是在给定条件下遍历寻求当前的最优解,求取的每一粒层决策阈值对具有不稳定性;而博弈论是求边界域不确定性与决策正、负区域错误分类率的平衡,相对多目标决策而言,所求阈值对结构更符合序贯三支决策模型的阈值假设,具有更合理的考虑.
综上分析可知,通过综合考虑边界域不确定性与决策正、负区域错误分类率,既追求错误率较小的同时也保证快速决策的效率.本文所提基于博弈论的序贯三支决策模型能获得较好的效果,在实际应用场景中具有一定的应用价值.
6 结束语
现有序贯三支决策模型的研究从提高分类精度或减少分类不确定性方面进行决策阈值的求取,缺乏对二者的综合考虑.为了解决这个问题,本文从博弈论的视角下构建了决策正、负区域错误分类率与边界域不确定性博弈的机制,并提出了求取每一粒层自适应决策阈值的优化模型.为了比较模型的效果,设计了基于TOPSIS 的多目标决策方法,利用10 个UCI 标准数据集进行了对比实验.实验结果验证了博弈论的序贯三支决策模型所求决策阈值结构的合理性.进一步地,通过与多目标决策方法的错误分类率进行对比,验证了博弈论的序贯三支决策模型效果的有效性.
——博弈论

