一种基于门限与感染技术的SM4算法综合防护实现
焦志鹏,姚 富,陈 华,王 舰,匡晓云,黄开天
(1.中国科学院软件研究所可信计算与信息保障实验室,北京 100190;2.中国科学院大学,北京 100049;3.南方电网科学研究院,广东广州 510663)
1 引言
物联网等技术的发展便利了人们各方面的生活,与此同时也使得个人隐私等秘密信息的保护面临着巨大的挑战.灰盒模型攻击的出现使得密码设备的实现安全性受到了严重的威胁.侧信道攻击[1~4]和故障攻击[5]是灰盒模型攻击中两种主流攻击方法.能量分析攻击是应用最广泛的侧信道攻击手段之一,其中差分能量分析[6]因其实现简单、成本低廉以及功能强大等优点,被广泛用于对实际密码设备的攻击过程.针对于侧信道攻击的威胁,不同的防护理论陆续被提出,其中门限实现防护理论[7]因其兼具可证明安全以及实现代价相对低廉的优点得到了学术界更为广泛的研究和应用.除了侧信道攻击之外,故障攻击同样是密码设备实现安全性的重要威胁,差分故障攻击是故障攻击中经典的攻击方法[8].乘法感染技术通过随机化故障密文对于故障攻击进行防护,其具有较好的故障攻击防护效果,但是存在着随机数为0时易通过功耗曲线区分的缺陷[9].仅仅添加能量攻击防护的电路面对故障攻击时是不安全,反之亦然.目前,针对两类攻击的防护方案往往是两类防护策略的简单叠加,不仅会带来实现代价的大量增加,也可能产生未知的安全漏洞,因此在实现密码算法时应综合考虑能量和故障攻击方法,并对相应的防护方法进行结合.为达到综合防护的目的,目前已有一些综合防护方案被提出[10~14],但都存在着一定的问题.目前还没有一种通用的兼具安全性与实现代价的综合防护方案,仍需要针对具体的密码算法以及实现特点去具体构造防护方案.
SM4 算法是我国公布的第一个商用密码算法标准,在我国各个领域的信息保护中起着重要的作用[15].SM4 算法同样面临着能量攻击和故障攻击的威胁.针对能量攻击的威胁,相应的防护方案也随之出现,谭锐能等基于多路径掩码技术构造了SM4 算法抗能量攻击的防护实现[16],裴超等针对SM4 算法S 盒查表实现提出了一种掩码方案[17],李新超等提出并实现了SM4 算法S-box 的门限实现防护[18],魏曼等提出了一种SM4 算法的门限实现防护方法[19].在故障攻击防护方面,辛小霞等基于“校验-阻止”原理提出了SM4算法的一种故障防护方法[20].但是对于SM4 算法目前还缺乏综合防护方案.本文基于门限实现与乘法感染的原理提出并实现了针对SM4算法的综合防护方案,该方法可以抵抗2阶差分能量攻击,与此同时也可以抵抗差分故障攻击,并且对于能量与故障的组合攻击也具有对应的抵抗能力.
2 SM4算法二阶综合防护实现
2.1 综合防护方案
本文基于门限实现和乘法感染的思想构造了一种综合防护方案并以SM4 算法为例对于综合防护方案进行了实现,其整体框架如图1 所示,对于原始SM4 进行门限实现,在此基础上实现一路完全相同的冗余SM4门限实现,最终通过乘法感染对故障密文进行随机化,从而实现对于侧信道攻击和故障攻击的综合防护.
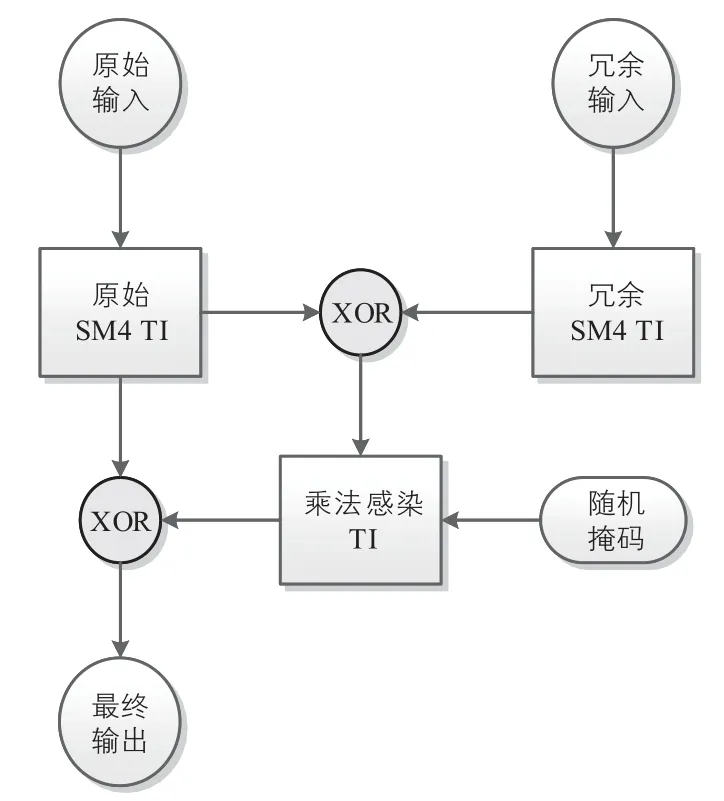
图1 SM4算法综合防护方案
为抵抗d阶差分能量攻击,需要进行d阶的门限实现防护.关于d阶门限实现,基于不同的考虑有多重变种,其中实现的面积消耗与划分的份额(share)个数正相关,为了达到降低面积消耗的目的,本文选取最低的也就是d+1 个share 进行门限实现,具体理论可以参考文献[21].d+1 share 实现的d阶门限防护带来实现面积优化的同时也对具体的门限实现有一些细节性的要求,如果实现不当可能会带来一些安全隐患.
对于线性运算来说,d+1 share的d阶门限实现是直接的.对于非线性运算的d+1 share 的d阶门限防护,其实现方法如下所示,单比特的乘法运算是综合防护实现的基本组成单元,因此这里以单比特乘法y=ab为例介绍d+1 share的d阶门限实现.
(1)输入变量的分解
使用布尔掩码将函数输入a和b分解为d+1份;首先利用2d份随机数生成前d份输入:(a1,b1,…,ad,bd),第d+1份输入可以由前d份输入和原始输入的异或生成,具体可以表示为(ad+1,bd+1)=最终构成需要的输入(a1,b1,…,ad+1,bd+1),由于随机数的存在,d+1份输入满足输入均匀性,也就是说每一种输入掩码都是均匀出现的.
(2)目标运算的分解
将步骤(1)中分解好的函数输入带入到目标运算y=ab中可以得到由掩码输入构成的新的函数表达式,由其组成项aibj,1≤i,j≤d+1,构成相应的输出函数需要满足正确性:y=,其中Sout表示输出函数的个数.另外为了达到安全防护的目的,d阶门限实现需要满足d阶不完整性,这里需要使得每个输出函数yk只包含一个组成项aibj,即输出函数的个数满足Sout=(d+1)(d+1).待防护的密码算法往往包含多轮的运算,因此会出现本阶段运算输出作为下一阶段输入的情况,为满足下一阶段的输入均匀性的要求,需要对输出函数进行重掩码,另外为了防止毛刺的影响需要在输出之前用寄存器进行存储;最后将(d+1)(d+1)份额的输出通过相互异或的方式压缩为d+1份作为下一阶段门限防护的输入.
针对故障攻击的威胁,综合防护方案利用乘法感染技术实现相应的防护.感染防护思想包括多重感染防护和只针对密文输出的单层感染防护,考虑到只针对末轮运算进行故障注入攻击的情况下多重感染将会失效,因此使用单重感染技术从而实现更少的资源占用.具体的实现方法是在原始SM4门限实现的基础上,冗余实现一路完全相同的SM4门限实现,将原始实现的输出和冗余实现的输出相互异或,然后利用感染函数将异或结果进行随机化,最后将感染函数的输出异或上原始加密的密文形成最终输出.在感染函数中,为了达到对于故障注入位置以及传播方式的防护,采用了一个随机数控制的置换操作以使得故障注入的错误随机扩散,增加攻击者的攻击难度,然后使用乘法感染技术达到对于故障密文随机化的目的.此外为了防止乘法感染部分侧信道信息的泄露,在乘法感染部分也进行了门限实现的防护,这种门限实现的方式也有助于改善乘法感染中随机数为0时的缺陷,达到了更好的故障防护效果,具体的更详尽的安全性分析见2.4节.
考虑到侧信道攻击技术的发展和相应设备的更新,针对密码算法实现能量分析攻击的代价越来越低廉,一阶门限实现的防护能力是有限的,因此本文在SM4算法综合防护实例中采用二阶门限实现,也就是3-share 的2 阶门限实现方案进行侧信道方面的防护,在实际的应用中可以根据不同的安全需求扩展到更高阶的门限实现.SM4 算法的综合防护实现主要由SM4 算法二阶门限实现部分和乘法感染部分组成,下面分别进行详细的介绍.
2.2 二阶门限实现
SM4 算法是32 轮Feistel 结构的分组算法,分组长度和密钥长度都是128 bit,加密结构和解密结构相同,只是加密密钥和解密密钥逆序,并且密钥扩展部分和加密结构类似,因此本文着重关注加密运算的防护实现,其防护实现可以方便地扩展到解密算法和密钥扩展结构.SM4以字为单位进行加密运算,包含32轮相同的轮运算,首轮输入的四个字可以表示为:(X0,X1,X2,X3);每轮迭代的轮函数可以表示为:Xi+4=F(Xi,Xi+1,Xi+2,Xi+3,rki)=Xi⊕T(Xi+1⊕Xi+2⊕Xi+3⊕rki),其中rki为轮密钥,0≤i≤31,由初始密钥扩展得到的,T由两部分组成,包括非线性运算部分和线性运算部分,非线性部分由四个相同的S盒运算组成,线性部分为移位操作,本实现中为了减少面积的消耗只实现一个S 盒,每轮执行4 次S 盒运算得到我们的输出.SM4 算法2 阶门限实现的步骤如下:
(1)使用随机数将输入明文从128 bit扩展为128×3 bit 的输入,分别存储在3 个128 bit 的寄存器中,(X0,X1,X2,X3)代表原始输入4 个字的3-share,也就是分别为32×3 bit,整个SM4 加密包括32 轮的运算,每一轮的运算需要11 个时钟周期,下面详细介绍第i轮运算,0≤i≤31.
(2)第0 个时钟周期,Xi+1,Xi+2,Xi+3与本轮的轮密钥相互异或生成32×3 bit结果.
(3)第0 到第3 个时钟周期将步骤(2)生成的32×3 bit 的结果构造为本轮所需的4 个S 盒运算的输入赋给S 盒,每个时钟的输入为8×3 bit,5 个时钟后产生输出,具体的S盒实现在下文将详细描述.
(4)第6 到第9 个时钟周期依次取出4 个S 盒的输出,每个S盒的输出为8×3 bit.
(5)第10 个时钟周期将得到的4 次S 盒的输出组合为32×3 bit 的数据,其中每个份额32 bit 分别执行线性移位操作,将线性移位后的32×3 bit数据与Xi相互异或得到轮运算结果.
(6)经过32 轮轮运算后,逆序输出即可得到最终的加密结果.
本方案中基于有限域的方式实现SM4算法的S盒.AES算法S-box可以看作是f(x)=x8+x4+x3+x+1上的求逆运算和仿射运算的组合,本文同样参考文献[22]的原理将SM4算法S盒运算看作为此不可约多项式上求逆运算和仿射运算的组合,从而可以方便地将AES S盒的构造应用到SM4 S 盒运算中去,具体可以得到SM4 算法S盒的代数表达式为:S(X)=A2(A1X+C1)-1+C2)其中A1、A2是仿射矩阵,C1=(0 0 0 0 0 0 0 1),C2=(1 1 0 1 0 0 1 1),A1、A2表示如下.

通过代数表达式可以看到,S 盒的非线性运算为GF(28)上的求逆运算,为方便门限实现,本文对其进行复合域分解.参考文献[23]的复合域实现方式,将GF(28)上的求逆运算转换为GF(2)上的运算.为结构图表述更加清晰,将其表示为GF(24)上的运算,其大致结构如图2 所示,主体部分包含非线性的3 个GF(24)上乘法器运算和一个GF(24)上的求逆运算(图中虚线部分),以及由常数乘运算以及平方运算组成的线性运算L1;对于乘法运算,最终被转换为GF(2)上的乘法运算;对于求逆运算,首先将GF(24)上的求逆运算转换为GF(22)上的运算,其包含3个GF(22)上的乘法运算以及由常数乘以及平方运算组合的线性运算L2,GF(22)上的求逆运算是线性运算,表示为L3,GF(22)上的乘法运算同样转换为GF(2)上的乘法运算.M1和M2代表仿射运算和逆仿射运算.
本文的S盒门限实现在图2复合域实现的基础上参考文献[24]进行防护设计,为了防止毛刺的影响以及保持门限实现的2阶不完整性,需要使用寄存器存储相应运算的输出结果,根据安全需要S盒的2阶门限实现需要分为6个阶段进行处理,每个阶段进行的操作如下所述.

图2 SM4算法S盒复合域实现
阶段1此阶段包含两个线性操作,首先是A1X+C1仿射操作,其次是基转换的转置矩阵,为了降低实现电路的复杂度,这里两种线性操作合二为一,为了安全性的需要,本阶段的输出需要使用寄存器存储以供下一阶段运算的使用.
阶段2此阶段主要包含一个GF(24)上的乘法运算以及一个线性运算,线性运算包含乘以常数操作以及平方操作两个运算,这里将线性运算和非线性运算相结合以减少输出份额的个数,从而减少存储所需寄存器的个数;这里输入为3-share 的,输出是9-share,L1代表这一阶段的线性运算,以(a1,a2,a3),(b1,b2,b3)代表此阶段输入a,b的 3-share 随机掩码,以(c1,c2,c3,c4,c5,c6,c7,c8,c9)代表门限输出,那么此阶段的运算可以表示为如下的表达:
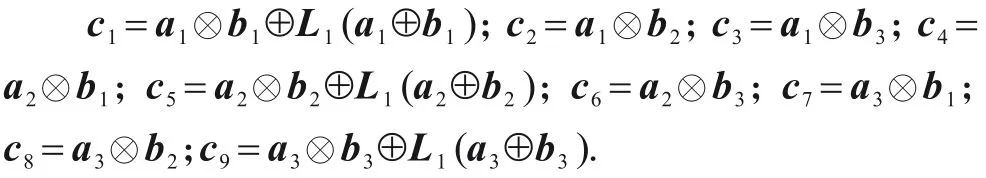
其中⊕代表4bit的异或运算,⊗代表4bit的乘法运算,由GF(2)上的乘法组合而成.一方面为了满足下一阶段输入的均匀性,另一方面为了达到抵抗多变量攻击的目的,这里对于(c1,c2,c3,c4,c5,c6,c7,c8,c9)使用随机数(r1,…,r6)进行重掩码,形成输出(O1,…,O9),掩码方式如图3所示,并且对于输出使用寄存器暂存.
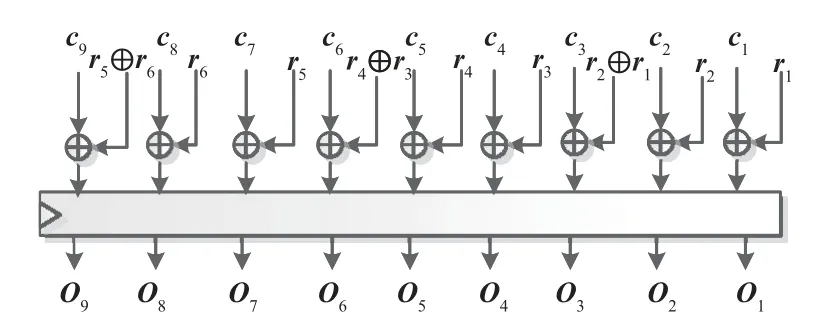
图3 重掩码
阶段3此阶段在GF(22)上进行运算,类似于阶段2 的运算,不过参与相应运算的数值从4bit变为了2bit.这里需要对上一阶段产生的9-share 输出压缩为3-share,这里需要小心操作,避免出现脱掩码情况的出现,本文实现中以O1⊗O4⊗O7,O2⊗O5⊗O8和O3⊗O6⊗O9的形式构造3-share 的输入,此阶段的输出同样需要进行类似于阶段2的重掩码,并对于输出使用寄存器进行暂存.
阶段4此阶段包含两个GF(22)乘法运算,首先需要将上阶段的9-share 压缩为3-share,然后经过一个GF(22)上的求逆运算L3,GF(22)上的求逆运算是线性运算只需要拉线操作计算产生3-share输出作为乘法运算的一个公共输入,另外结合阶段3 的输入构造两个GF(22)乘法的其他输入,两个乘法运算的9-share输出相互结合形成9-share的4 bit输出,对这个9-share输出进行与阶段2相同的重掩码,并将掩码结果存储在寄存器中.
阶段5此阶段类似于阶段4,只不过相应运算从GF(22)上的乘法运算变为GF(24)上的乘法运算;首先需要将上阶段的9-share 按照阶段3 的方式压缩为3-share 作为两个乘法的公共输入,另外结合阶段2 的输入构造两个GF(24)上的乘法的其他输入,两个乘法运算的9-share 输出相互结合形成9-share 的8 bit 输出,对这个9-share 输出进行阶段2 相同的重掩码,存储在寄存器中.
阶段6此阶段包含三个线性运算,首先将上阶段的9-share 输出按照阶段3 的方式压缩为3-share,其次是基的转置矩阵,最后是SM4 算法S 盒的仿射运算,类似于阶段1,本阶段同样将转置操作和仿射运算相互结合以降低实现电路的复杂度.
2.3 感染防护
在SM4 算法原始二阶门限实现的基础上实现一路与原始门限实现完全相同的冗余SM4 算法二阶门限实现,冗余实现的输入和采用的随机数与原始实现完全相同.将原始实现的输出和冗余实现的输出相互异或形成128×3 bit 的输出.如果没有故障注入时,异或输出为0,经过感染结构后的输出为0,最后异或到原始密文形成最终输出,不改变密文输出结果,保证了无故障注入时算法的正确性.当有故障注入时,异或输出不为0,然后将128×3 bit 的输出以32×3 bit 为一组分为4 组,分别进行感染防护,其中被故障注入影响的字节表现为随机数,与原始实现的输出相互异或形成最终的密文输出,相应的可被利用的故障密文也被随机化了,从而实现了相应的故障防护.其中感染防护由随机置换和乘法感染两部分组成,具体结构如图4所示.
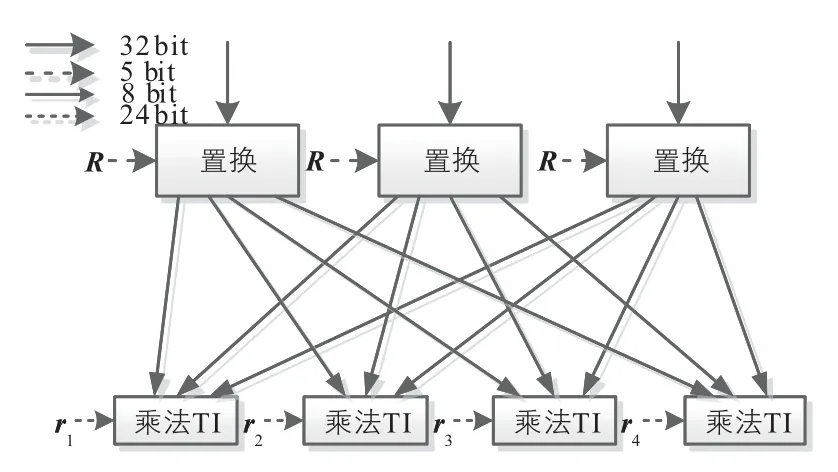
图4 感染函数
为了隐藏故障注入的位置以及故障的传播路径,在进行感染操作之前进行一个32 bit的随机置换操作.具体的在进行乘法感染操作之前,先进行32 bit 的置换操作,初始置换操作(位置标号从0开始)如下:

此置换由一个5 bit的随机数R控制,以此增加其随机性,具体是在每一次感染的时候将初始置换进行一个随机的循环移位操作后作为此次感染的置换操作.
经过置换操作后的32×3 bit 的输出以8×3 bit 为一组和随机数(r1,r2,r3,r4)进行GF(28)上的以f(x)=x8+x4+x3+x+1 为不可约多项式的有限域乘法运算,这里的乘法运算为了防止侧信道信息的泄露也使用了二阶门限实现进行防护,能够有效改善乘法感染中随机数为0 时的缺陷.此外感染防护中的随机置换对于故障传播途径进行了随机化,使得攻击者无法直接进行攻击,从而进一步增强了故障防护效果.
2.4 安全性分析
2.4.1 针对侧信道攻击的安全性
综合防护方案对于侧信道攻击的防护能力继承于门限实现.一个d阶的门限实现满足输入的均匀性,d阶不完整性;d阶能量攻击可以同时利用d个综合防护方案的中间值的能量信息进行攻击,而门限实现的d阶不完整性使得这d个中间值至少和原始中间值的一个分量相互独立,也就是和原始中间值成相互独立的关系,使得d 阶能量攻击者能够利用的信息与原始中间状态相互独立,从而实现了d阶能量攻击下安全性.
具体到本文的SM4 算法的综合防护实现,本文的综合防护实现中加密部分和乘法感染部分都基于2 阶门限实现进行了防护,其满足2 阶不完整性,一个2 阶能量攻击者可以同时利用2 个综合防护的中间值的能量信息,这2个中间值和原始中间值呈现相互独立的关系,使得2阶能量攻击者能够利用的信息与原始中间状态相互独立,从而实现了2阶能量攻击的安全性.
2.4.2 针对故障攻击的安全性
数值类的故障攻击如差分故障攻击,其攻击条件首先是需要知道故障密文,其次需要分析故障传播路径,因此可以从这两方面实现相应的防护.在本文综合防护中,一方面随机置换的添加使得故障密文扩散呈现随机性,增加了攻击者对于故障攻击位置以及传播逻辑分析的难度,另一方面乘法感染技术使得输出的故障密文呈现随机性,破坏了输出的故障密文和原始故障密文的相关性,使得需要故障密文的故障攻击无法顺利进行,从而实现了对于数值类故障攻击的防护.
2.4.3 针对组合攻击的安全性
如前文提到的乘法感染在随机数为0 时存在缺陷,此时能耗信息较小,然后攻击者可以依据这一点判断出随机数为0时的故障注入,筛选出故障攻击需要的故障密文,从而实施正常的依赖故障密文的故障攻击,此类攻击方法属于一种组合攻击.普通的GF(28)的乘法运算中,只有8 bit 的随机数参与运算,找到一个8 bit 的为0 随机数的情况,相对容易,在本文的综合防护中对于乘法感染同样实现了门限实现防护,由于进行3-share 的门限实现防护,只有在3×8 bit 的随机数同时为零的情况下,功耗才容易被分辨出来,实现的困难性大大增加;同时即使找到了3×8 bit 随机数为0 的情况,其故障攻击仍然存在困难性,因为本文的综合防护的乘法感染防护中进行了随机置换操作,随机化了故障传播的路径,使得实际的故障攻击的逻辑分析仍然存在着困难性,因此可以实现对于此类组合攻击的防护.
另外本文的综合防护方案对于故障注入-探测类型的组合攻击同样有着抵抗能力,在此类攻击中,攻击者通常先通过故障注入的方式将某些中间值置位为0,然后通过探测的方式实现对于原始中间值的获取.在本文的综合防护方案中,即使注入了对应的故障,如将某些中间值分量置位为0,这同样不会导致敏感信息的泄露,因为门限实现的d阶不完整性使得d阶探测的攻击者仍然无法获取原始中间值的有效信息.
3 实验结果
3.1 实验环境
本文在SAKURA-X 评估板上实现了我们的综合防护方案,SAKURA-X 是一种专门用来进行侧信道防护方案实现和评估的开发板,主要包含两个FPGA(Field Programmable Gate Array),一个是评估FPGA,用于实现待测方案,我们的综合防护方案实现在其中;另一个是控制FPGA,用来控制评估FPGA 和上位机的通信,为避免噪声的影响,随机数发生器实现在其中,使用时传输相应的随机数到评估FPGA中.
3.2 安全性评估
3.2.1 侧信道安全性评估实验
在评估环境设置方面,我们采用便于侧信道攻击的方式进行评估实验,比如:(1)为了降低采集到的功耗信息的噪声,提高信噪比,本文将随机数的产生逻辑和综合防护的实现放在了不同的FPGA 中;(2)为了能够使得采集到的功耗曲线更加清晰,我们使得综合防护实现工作在低频状态,具体在本文的实现是工作在375 kHz 的时钟下.在如此便利于攻击者的情况下,如果可以验证本文防护方案的安全性,那么在实际的攻击环境中,综合防护的安全性是可以得到保障的.
我们采用测试向量泄露评估技术(Test Vector Leakage Assessment,TVLA)[25]进行侧信道安全性的评估,它是一种从信息泄露角度评估防护方案安全性的一种技术.其中不针对具体中间值的non-specific TVLA 评估技术是应用最广泛的评估技术,需要收集两组分别是固定输入和随机输入的功耗曲线,当评估高阶泄露时,需要进行合适的预处理,预处理后的曲线作为TVLA 待测曲线;其通过t-test 技术评估两组曲线分布均值的差异性,从而判断是否有泄露的产生.本文选择正负4.5 作为统计量的阈值,其置信度大于99.999%,当其统计值低于阈值时,则表明通过了测试,当统计值超过阈值时,则表明其存在泄露点,相应的防护方案可能存在易损点,d阶TVLA 与d阶差分能量分析相对应,当其通过TVLA,则可认为相应的防护方案是d阶差分能量分析安全的.S 盒是防护方案中主要的非线性组件,S 盒的侧信道安全性可以反映整个防护方案的安全性,本文主要测试S 盒的侧信道安全性.
本文使用PicoScope 3206D 示波器在125 MHz 的时钟下对于待测方案进行功耗采集,分别在随机数关闭(无防护)和随机数开启(有防护)状态下采集100 万功耗曲线进行了TVLA 安全性评估.其一阶TVLA 评估结果如图5 所示,其二阶TVLA 评估结果如图6 所示.
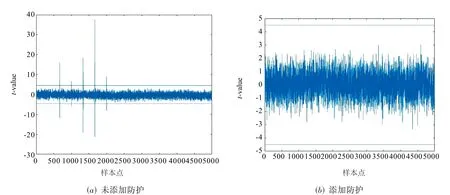
图5 一阶TVLA测试结果
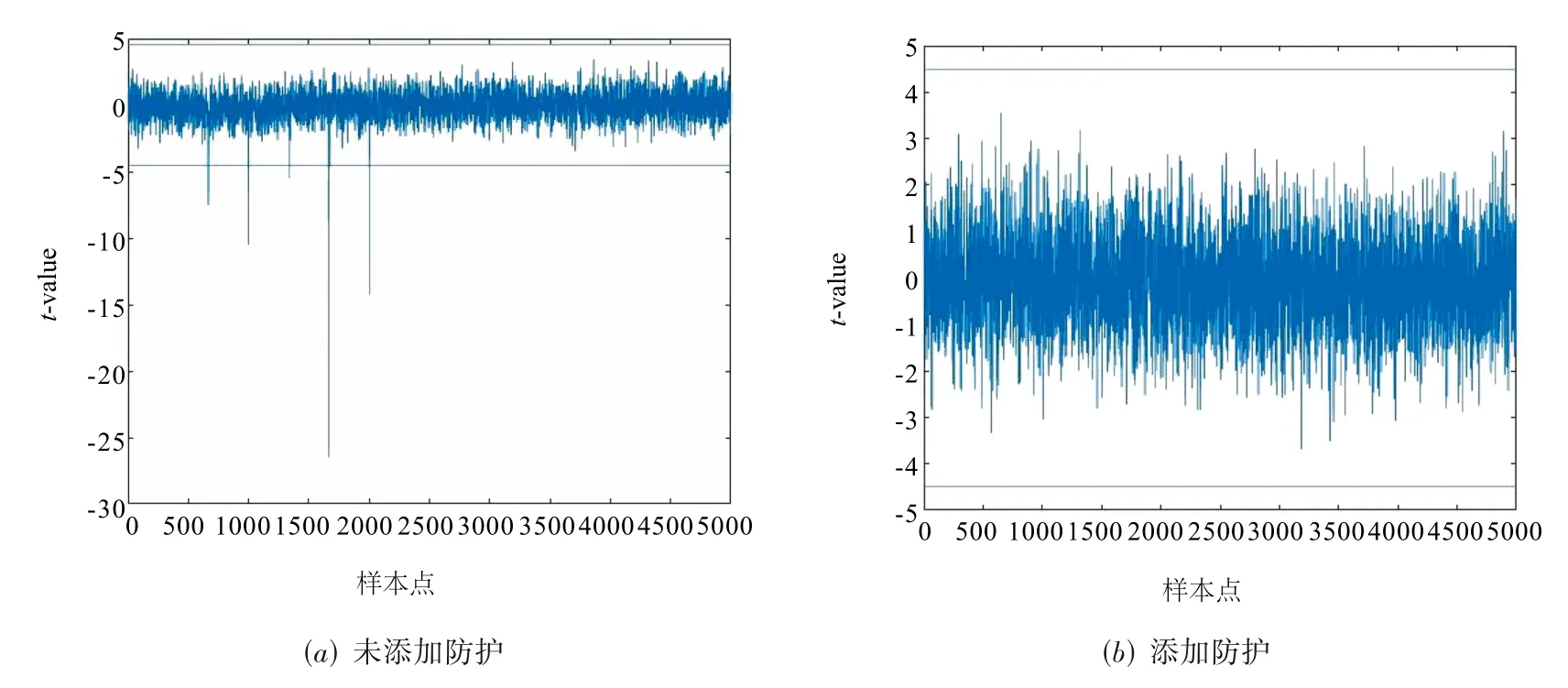
图6 二阶TVLA测试结果
图中横轴代表S 盒执行过程中不同时刻采集到的样本点,纵轴代表t测试统计量.从实验结果中,我们看到未添加防护的情况下,统计量都超过了4.5,添加防护后统计量都未超过4.5,验证了我们的防护方案在侧信道安全方面具备抵抗一阶差分能量攻击和二阶差分能量攻击的防护能力.
3.2.2 故障攻击安全性评估
我们通过对SM4 算法的最后一轮的S-box 输入注入故障来检测综合防护方案的故障防护的安全性,通过分析经过感染结构的故障密文的随机性验证综合防护方案的故障防护的能力.具体的,选择SM4 算法最后一轮运算中的任意一个S-box 运算,在综合防护实现代码中将选定的S-box 输入置位为常数,从而实现对于故障注入的模拟,然后将此代码生成的流文件下载到FPGA 中去,然后执行100 万次明文、密钥相同的运算,然后记录密文输出中被故障注入影响到的故障密文,也就是共400 万字节的故障密文,最后统计故障密文的随机性,如果故障密文呈现良好的随机性,那么证明本文的防护方案起到了针对故障攻击的防护效果.
对于记录的故障密文使用NIST SP800-22 给出的项目和参数进行随机性检测,检测中单样本大小是20000 B,总样本数是200,其检测结果如表1所示.
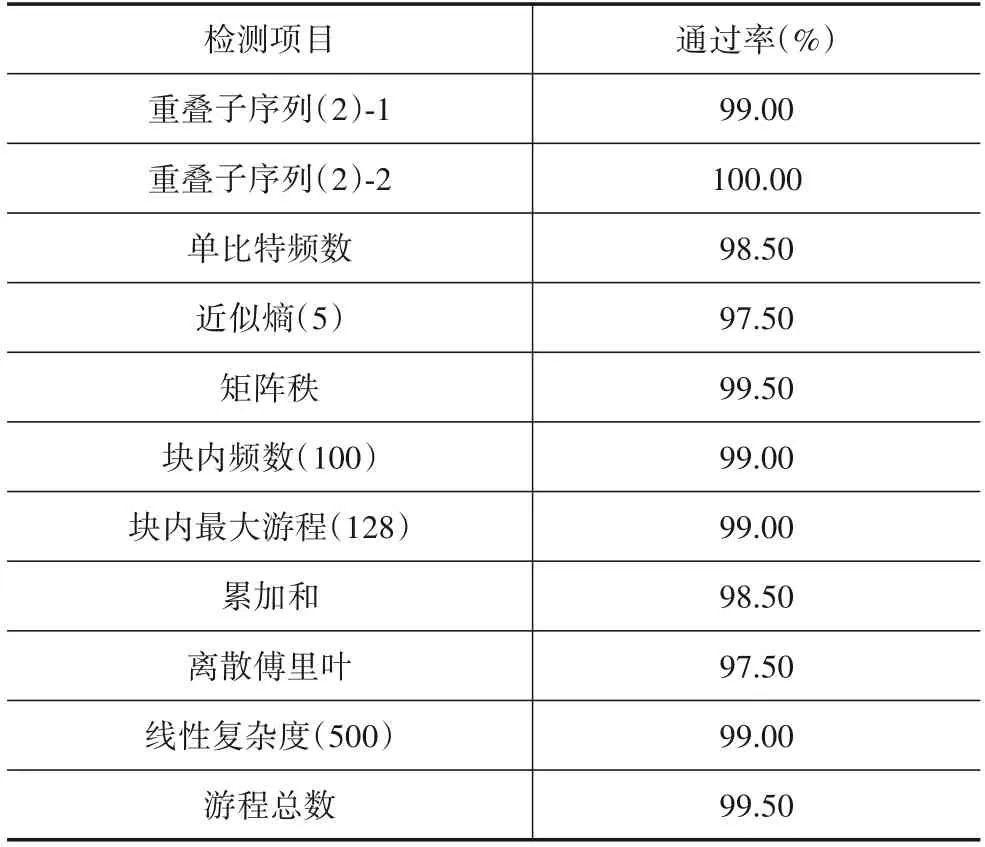
表1 随机性检测的统计结果如下(通过检测的百分比:阈值下限96.889)
检测结果表明故障密文通过了随机性检测,经过感染后的故障密文具有良好的随机性,可以达到相应的防护效果,验证了综合防护方案对于故障攻击的安全性.
3.3 实现代价评估
我们使用ISE 14.7 验证了SM4 算法综合防护实现的功能性,使用Synopsys 2016.03 在NanGate 45 nm 公开元件库下评估了相应的面积消耗,无防护情况下的SM4 算法的面积消耗如表2 所示;SM4 算法综合防护的面积消耗如表3 所示,其中“SM4 原始门限实现”与“SM4 冗余门限实现”完全相同,面积消耗完全一样,因此只展开列出了“SM4 原始门限实现”组成部分的面积消耗情况.
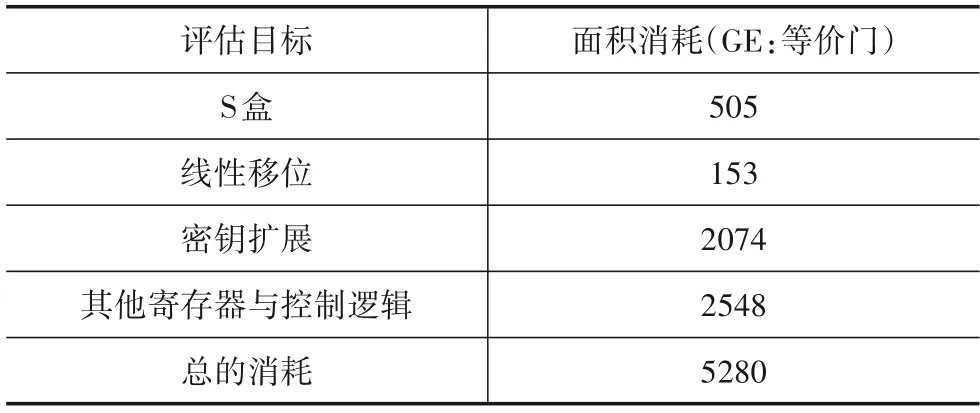
表2 SM4算法无防护实现面积消耗
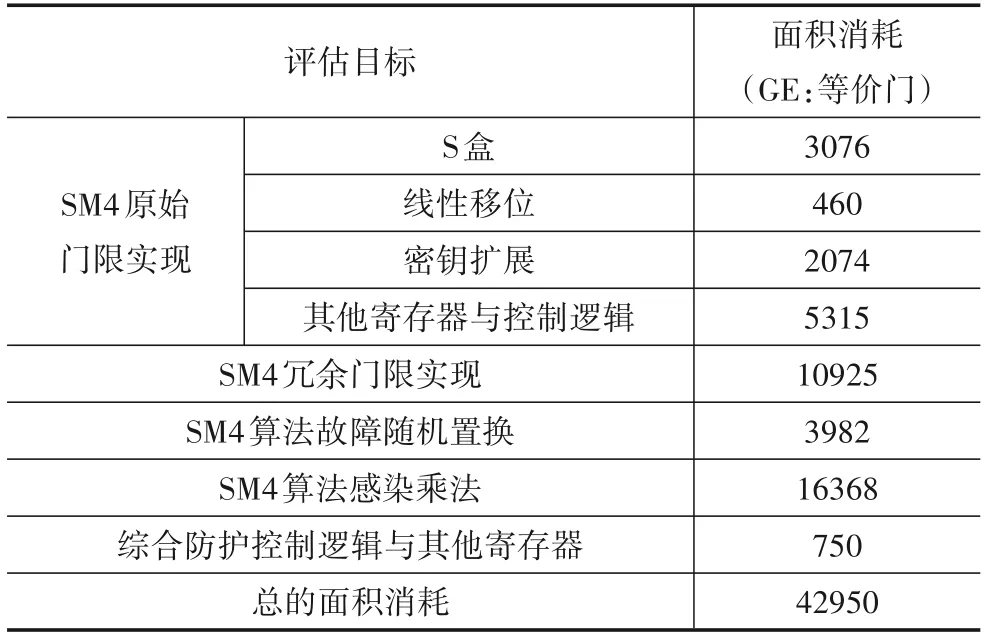
表3 SM4算法综合防护实现面积消耗
本文中SM4算法综合防护方案每轮使用11个时钟周期,共32 轮,所以整个防护方案使用了352 个时钟周期;在随机数方面,每个S 盒运算使用了108 bit 的随机数,感染结构中的随机置换部分使用了20 bit 的随机数,乘法感染部分使用了384 bit的随机数.
4 结论
考虑到灰盒模型攻击的巨大威胁,本文结合门限实现和感染防护的思想提出了一种综合防护方案,通过门限实现弥补了乘法感染故障防护中随机数为0 时的缺陷,另外通过添加随机置换的方式掩盖了故障注入位置和故障传播逻辑,进一步强化了对于故障攻击的防护能力.并且本文以SM4 算法为例在FPGA 上实际实现了一个二阶综合防护方案,为SM4 算法针对侧信道攻击和故障攻击的综合防护提供了一种方案.最后本文通过安全性分析以及实际的实验验证了SM4 防护方案的有效性,并评估了相应的实现代价.

