弧面分度凸轮廓面数控加工工艺分析

蔡 君

（上海杰兴汽车配件制造有限公司， 上海 200000）

引言

弧面分度凸轮机构发明于19 世纪20 年代，可以实现不同转盘半径之间的曲面转移，满足制造业的标准化生产需求。除此之外，弧面分度凸轮的精度高，使用稳定，因此得到了广泛的应用[1]。就设计理论而言，常见的弧面分度凸轮有两种设计方法，即绘制法和分析法，这两种方法都以反演法为理论技术，将弧面分度凸轮作为一种空间凸轮进行设计[2]。但由于弧面分度设计复杂，其工作轮廓是一个不能扩展的曲面，因此很难测绘，且目前传统的弧面分度凸轮廓面数控加工工艺的精度低，无法满足加工需求，因此设计了新的弧面凸数控加工工艺。

1 弧面分度凸轮廓面数控加工工艺设计

1.1 设计弧面分度凸轮机构

弧面分度凸轮设计过程中应充分考虑动盘的运行规律，设置凸轮机构的重要参数，其中包括运动参数、几何参数两部分。运动参数的设置准确性决定了弧面分度凸轮的运行状态；几何参数的设置内容包含分度轮廓头数、凸轮分度周期旋转角度、凸轮停止周期旋转角度、驱动转盘速度、滚子数量、转盘运行动态停止比、运动系数等，决定了凸轮和凸轮机构的特定尺寸转台设计[3-5]。几何参数用于确定转盘、凸轮等零件的具体尺寸，凸轮机构的运动参数主要分为两种，即凸轮旋转运动参数和从动转盘运动参数，根据设计目的运动规律进行参数公式设定，转盘转一圈所停分度数E 如下：

式中：M 为滚子个数；N 为凸轮头数。

凸轮的转速v 是凸轮单位时间内完成的分度次数：

动停比k 指从动件转盘的旋转时间t1与停歇时间t2的比：

全部参数如表1 所示。

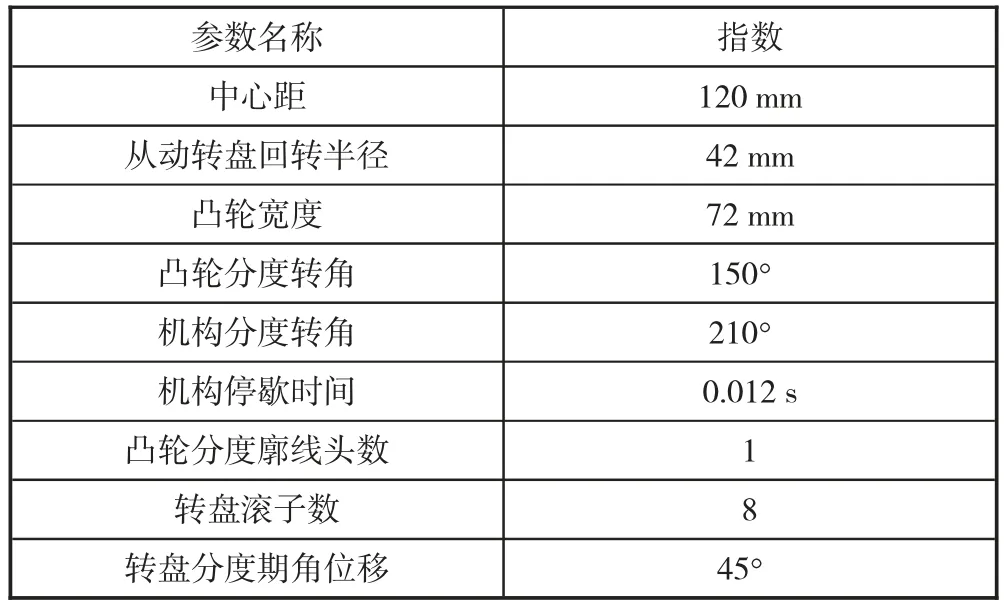
表1 运动参数表

由表1 可知，设计的弧面分度凸轮机构为单头结构，该结构在实际运行时凸轮呈匀速运动。在凸轮匀速运动时，转盘处于间歇运动状态，即分度循环状态或间歇循环状态。当转盘处于分度循环状态时，凸轮转动角度与分度值呈正比，直接影响到凸轮机构的运行状态[6]。当转盘处于间歇循环状态时，凸轮机构运行则较为平稳。当转盘处于闲置状态时，凸轮机构也处于闲置状态。

弧面分度凸轮机构的主要设计思路是动件的间歇运动，整体运动过程包括分度期和休止期。凸轮机构在分度运动时，驱动盘转动的角度就变为转盘的分度角[7]。凸轮转动时，从动转盘为保证外倾式分度凸轮机构的平稳运行和连续传动而不发生突变，需要保证前滚轮不脱离凸轮工作面，后滚轮与凸轮工作面完全啮合，且啮合位置具有高度一致性，此时如果不调整传动角度，凸轮面和滚子会慢慢卡住，此时凸轮机构如图1 所示。

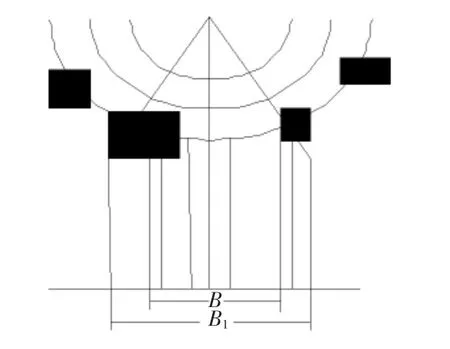
图1 弧面分度凸轮机构

由图1 可知，凸轮的旋转方向分为左、右两种，由于凸轮在设计时需要预先计算实际的凸轮宽度，因此需要预先设定凸轮的转速，凸轮的截面直径反映了凸轮工作轮廓底面与凸轮上弧圆的距离。相邻两个轴的距离与其他因素有关。凸轮的理论宽度指凸轮的工作轮廓与相邻两个轴线之间的距离，为了获得更好的啮合性能，滚子的半径通常在0.5～0.7 mm之间。

1.2 选取弧面分度凸轮工作曲面

设计弧面凸轮的的实际工作曲面，应根据空间共扼曲面原理，应用矢量坐标变换的方法，设计弧面分度凸轮工作曲面如图2 所示。

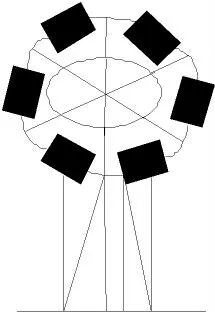
图2 凸轮工作曲面

由图2 可知，在该工作曲面上进行加工，考虑到此时在高速重载工况进行加工，因此在设计的弧面分度凸轮机构中采用高强度材质的凸轮曲面，该材质为硬质合金，其具备高强度、高耐磨性等性能。凸轮的表面硬度必须高于滚轮表面的硬度[8]，为有效保护凸轮轮廓，凸轮分度材料的合理选择和热处理工艺的正确实施是加工关键。

本文使用5 轴联动加工中心DMLTS，进行弧面分度凸轮的精加工。在使用5 轴联动加工中心进行加工前，应先使用车床对毛坯进行车削处理，直到毛坯达到最大半径，选择三个夹头固定凸轮毛坯，确保毛坯与工作台的旋转中心保持固定。装夹完成后，启动机床，进行自动加工。

二次粗加工时采用流线铣削，最大限度地去除多余材料，保持粗加工凸轮毛坯的轮廓面加工余量尽可能恒定，保证加工刀具能沿既定的流线旋转。粗加工时，使用46 mm 的球头铣刀用于外倾型分度凸轮的精加工，同时通过加长刀架固定，保障刀具的稳定性，进而保证凸轮处理平稳，机床运行不受其他错误信息影响。

1.3 进行数控加工误差分析

数控加工即运用小于圆弧分度的凸轮机构刀具实现非等效加工，解决数控加工中的精度问题。非等效加工的误差只能通过合理的刀具定位尽量最小化。为了使用非等效加工方法加工弧面分度凸轮，需要根据截面加工理论对加工的弧面分度凸轮的轮廓误差进行分析。

分析误差首先需要研究刀具位置与弧面分度凸轮补偿方向的关系。以设计的圆弧分度凸轮为研究对象，分度器件滚子半径R=20 mm，机构中心距C=180 mm，圆弧分度凸轮的转角为1500°，滚轮高度h=20 mm，滚轮内表面到旋转中心的距离h=70 mm。根据面加工原理，此时凸轮的轮廓面是一条扭曲的格线。

刀具的实际工作面呈包络线曲面状，因此会导致滚子中点偏移方向计算存在误差，但只要将误差控制在一定范围内也同样能够满足加工需求即可。包络线曲面如图3 所示。

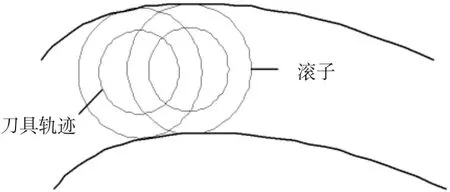
图3 刀具包络滚子示意图

根据图3 可知，刀具中心轴和滚子中心轴的距离：

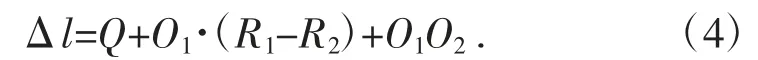
式中：R1为滚子小端半径；R2为刀具的半径；Q 为滚子中心轴底部到顶部的矢量；O1、O2分别为刀具的中心位置和滚子的中心位置。

将每个有效触点依次作为补偿方向，避免滚轮轴参数发生变化时，产生误差变化。补偿公式为：

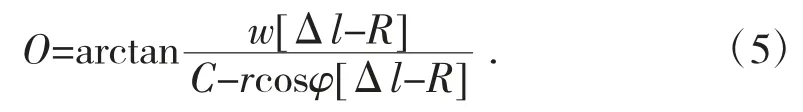
式中：φ 为滚子的位置角；C 为中心距；w 为运动系数；r 为滚子的曲面参数。

1.4 实现弧面分度凸轮廓面数控加工

传统的加工方法包括手绘法、逐点比较法、仿制法、数控仿制法等。弧面分度凸轮和滚子啮合按照设计的运动规律同时旋转，即处于空间共轭运动状态，被加工体在加工过程中一直处于匀速旋转状态。等效加工再现了滚子与凸轮啮合运动的关系，加工出的凸轮轮廓理论上无误差。因此，加工弧面分度凸轮的机床，除了传统的三轴连接外，还需要工件的旋转和工件的相对摆动。

刀具的几何形状与滚轮相同，因此可以在加工完成后获得满足要求的凸轮。主轴摆角和凸轮转角加工时，必须使用特制刀具，且刀具的形状必须始终保持恒定。凸轮槽的形状限制了加工工具的灵活性，因此需要根据凸轮的设计特点，计算机床的几何参数。从动盘的滚轮尺寸由实际工况决定，必要时需定制刀具，因此不可避免地增加了加工凸轮的成本。

弧面分度凸轮机构是一种高间断机构，从凸轮轮廓面方程可以看出，只有当凸轮处于间歇期时，理论接触轨迹才是直线，实际接触轨迹是加工刀具与加工轮廓面共轭接触的空间曲线，只要采用单面凸轮加工法，就会出现加工理论误差，需要选择合理的刀具位置，尽可能增加匹配度，减少加工误差。

根据弧面分度凸轮的动力学与运动学特性建立准确的曲线求解方程。建立坐标系Z-OXYZ 后，即可准确修正正弦加速度的运动规律。在坐标系可写出滚子在啮合点的方程式如下：

式中：R 为滚子的半径；β 为工作面的曲面参数。

滚子的位置角如下所示：

式中：s 为无因次位移；p 为凸轮旋向；φ0为滚子起始位置角；φ1为滚子的角位移；φ2为转盘分度期转角。

根据曲面的设计基本条件，在共辄接触点处两曲面间的相对运动速度必须垂直于其公法线，可求得凸轮的通用共轭接触方程如下：

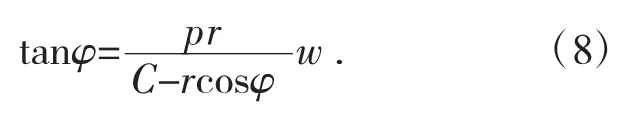
由式（6）—式（8）联立得到曲面公式：

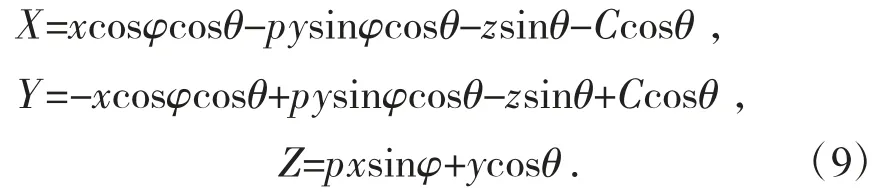
式中：θ 为凸轮转件。

2 工艺分析

2.1 分析准备

根据加工的实际要求，设计了弧面分度凸轮，确定了凸轮的尺寸参数和凸轮的外形。为了保证分析的准确性，将弧面分度凸轮的尺寸缩小2.5 倍，使用5轴加工设备，根据实际加工能力限制，将毛坯半径设置为41.00mm 的铝合金，同时，将毛坯长度设置为15 mm，考虑到刀具进退时与设备的碰撞，以及加工中心的实际结构和凸轮加工方式，选用指定的器械作为加工照明器，凸轮组加工如图4 所示。

图4 数控粗加工工件

由图4 可知，粗加工的工件不符合当前的分析要求，必须进行二次加工。为了保证加工准确性，加工曲线分度凸轮的毛坯选用尺寸为100 mm×150 mm 的铝合金，立铣刀直径设置为41.00 mm。二次加工后曲线分度的凸轮轮廓底部尺寸会变形小，易干扰立铣刀的加工，应参考加工手册，采用球刀加工陡峭的表面，球刀可以在加工过程中保持切削状态，使曲面的误差分布更加均匀，因此，球刀可以保证工件符合分析要求，二次加工工件如图5 所示。

图5 二次加工工件

根据图5 的二次加工工件状态，进行工件加工循环，记录循环参数，为后续工件的精度检测提供检测依据。

2.2 应用效果与讨论

分别使用本文设计的工艺和传统的工艺进行弧面分度凸轮廓面数控加工，记录此时各个工艺的指标，分析结果如表2 所示。

由表2 可知，本文设计的加工工艺在进给速度和主轴转速方面均优于传统的工艺，因此本文设计的工艺加工精度更高。

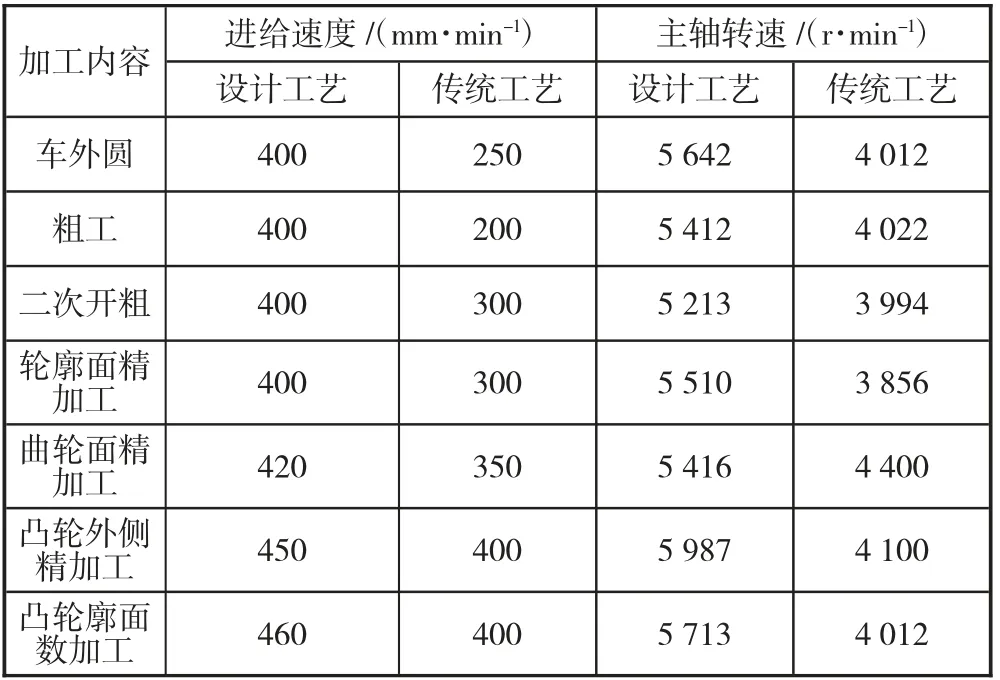
表2 设计工艺与传统工艺加工指标

3 结语

本文根据弧面分度凸轮的等价加工理论，在传统的弧面分度凸轮廓面数控加工工艺的基础上设计了新的加工工艺，通过弧面选取和误差加工优化了工件的加工状态，进行工艺分析，分析结果表明，设计的工艺各项指标均优于传统工艺，设计工艺的加工精度高，加工效果好，有一定的应用价值。