《平均数》教学设计

文|周秋容

【教学内容】

人教版四年级下册“平均数”。

【教学过程】

一、智导——创设情境，提出问题

1.体验投篮，情境激趣。

师：同学们喜欢体育运动吗？四年级3班的同学正在进行投篮比赛，咱们一起去看一看。（观看视频）

【设计意图：兴趣是最好的老师，一个人一旦对某事物有了浓厚的兴趣，就会主动去求知、去探索、去实践，并在求知、探索、实践中产生愉快的情绪和体验，全身心地投入到学习中。】

2.发现信息，提出问题。

师：老师要从他们当中选出一名成绩最好的同学参加全校的比赛，现在有两名同学成绩都很优秀。（出示成绩表）

陶安平

?

刘俊熙

?

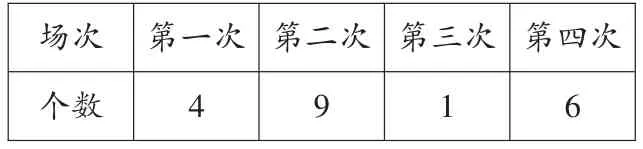
师：请同学们帮助老师选一选，应该派谁来参加全校的比赛呢？

预设：比总个数；比较他们平均投的个数；比较最多投的个数。

师：有的同学想比较总个数，有的同学想比较平均每次投篮的个数，还有的同学想比较最多的个数，大家认为哪种方法最公平？

预设：比较平均每次投篮的个数更公平。

二、研学——自主尝试，探究问题

1.探究求平均数的策略。

师：看来同学们都认为比较平均每次投的个数更公平，也就是让平均每次投的个数同样多。（板书：同样多）

师：怎样才能使平均每次投的个数同样多？我们借助条形统计图来帮忙。请你先独立思考然后小组交流。开始！

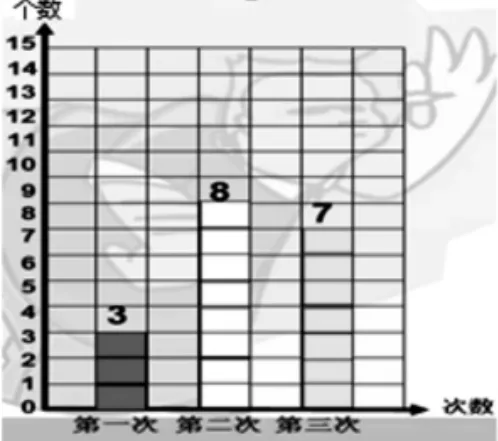
2.感知求平均数的方法。

小组派两名代表汇报。

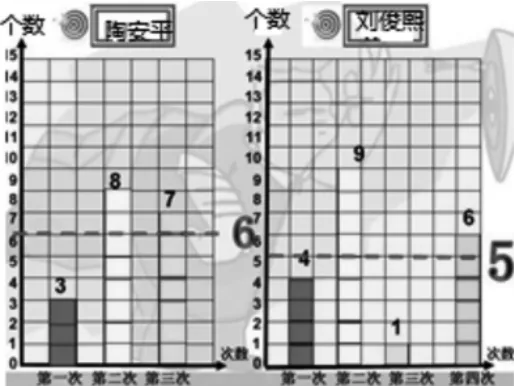
第一组：我以第一次为标准，移动后使三次投篮的个数同样多。

师：平均每次投篮多少个？

预设：6个。

第二组：我以第一次为标准，把多出来的都拿走，再一个一个往上加，就同样多了。

师：平均每次投多少个？

预设：6个。

师：刚才同学们用不同的方法得到了陶安平同学平均每次投6个，虽然移动的先后顺序不同，但是都是把个数多的补给少的，最终使每次投的个数同样多。在数学上，我们把这种移动的过程称为移多补少。（板书：移多补少）

师：我们把移多补少得到的这组同样多的数叫做这组数的平均数。（板书：平均数）陶安平同学三次投篮个数的平均数就是6。

（课件演示移多补少）

师：请大家边看课件边思考：1.我们用什么方法得到陶安平同学3次投篮的平均数？2.这个平均数是几？3.它是哪几个数的平均数？

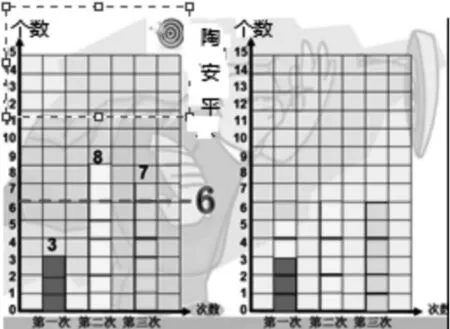
师：6是第一次投篮的个数吗？是第二次投篮的个数吗？是第三次投篮的个数吗？

预设：不是。

师：那是什么呀？

预设：是三次成绩的平均数。

师：它是我们通过移多补少找到的中间数，这个6是确实存在的数吗？

预设：不是。

师：我们可以用虚线表示这个平均数。它反映的是陶安平同学3次投篮个数的整体水平。（板书：整体水平）

【设计意图：“平均数”与“平均分得的结果”是不同的概念。平均分得的结果是一个实实在在的量，而平均数只是一个表示中间状态的抽象数量，这里又一次让学生真切地感受到“平均数”的实际意义。】

师：刘俊熙同学平均投篮的个数又是多少呢？你能结合刚才的操作经验，再来试试吗？

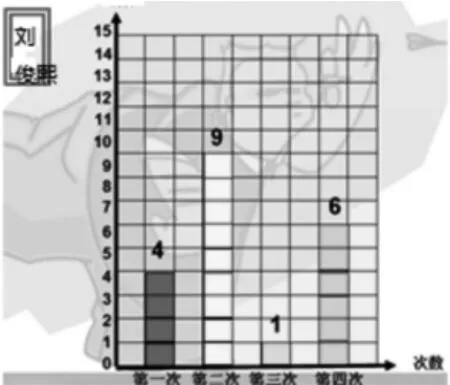
小组讨论：哪个小组来说说你们是怎么做的，结果怎样？

预设：我们以第三次为标准，平均每次投篮的个数是5分。

师：用的什么方法？

第二组汇报

师:虽然同学们移动的先后顺序不一样，但是用的都是移多补少的方法，得到了刘俊熙同学4次投篮个数的平均数，是几啊？

预设：5个。

师：这个5个是谁的平均数？

预设：4、9、1、6。

师：这个5是确实存在的数吗？

预设：不是。

师：我们可以用虚线来表示。它反映的是刘俊熙4次投篮个数的整体水平。

3.理解平均数的意义。

师：现在大家知道该派哪位同学上场了吧？

预设：陶安平。

师：陶安平同学上场后果然不负众望，第四次投篮个数是10个！

师：陶安平现在的平均分还是6个吗？你感觉是多少？可能是3吗？可能是10吗？为什么？

师:我们用移多补少的方法把多的数补给少的数，这样小的数就变大了，大的数变小了，所以平均数在最大数和最小数之间。这也是平均数的一大特点。（板书：最大数和最小数之间）

4.尝试求平均数的计算方法。

师：到底是多少呢？同学们动笔算一算。

预设：（3+8+7+10）÷4=7个。

师：括号里求的什么？为什么÷4？

（课件出示：先合后分的过程略）

板书：总数量÷总份数=平均数（先合后分）

【设计意图：“先合后分”这一环节的设计，让学生清楚地认识到在计算平均数的时候要先把几次投篮的个数都合起来，然后再平均分。这样有助于学生理解平均数的意义和掌握求平均数的方法。】

师：我们可以用移多补少的方法得到四次的平均成绩。也可以用计算的方法把所有投篮的个数都加起来平均分成4份，得到平均数是7。

师：请大家继续思考：刚才陶安平同学第四次投篮的个数是10个，平均数是多少？如果第四次只投了2个，那平均数会变吗？是几呢？动笔算一算。如果第四次只投了6个，平均数是几？

5.理解平均数的内涵。

师：同学们看看这个表格，你有什么发现？

预设：前三次的数据没有变化，只有第四次发生变化，平均数就发生了变化。

师：只要一个数据发生变化，一组数据的平均数就会发生变化。难怪有人说，平均数很敏感，任何一个数据的风吹草动，都会使平均数发生变化。学到这里，你认为平均数有什么特点呢？

预设：容易变化。

师：平均数容易随着数据的改变发生变化，这是平均数的又一个特点。（板书：易变化）

师：同学们继续观察，平均数还有什么特点？

（课件出示：超出平均数的部分=不到平均数的部分）

师：大家有没有发现这里有些数据超过了平均数，而有些数据还不到平均数？比较一下超过的部分与不到的部分，你发现了什么？

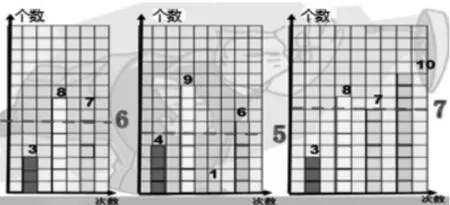
预设：超过的部分和不到的部分一样多。

师：为什么？

预设1：如果不一样多，超过的部分移下来后不能把不到平均数的部分填满，就得不到平均数了。

预设2：就像山峰和山谷一样把山峰切下来填到山谷里，正好可以填平。如果山峰比山谷大，或者山峰比山谷小，都不可能正好填平。

师：多生动的比喻啊！其实像这样超出平均数的部分和不到平均数的部分同样多，这是平均数的又一个重要特点，把握这一特点我们可以巧妙的解决相关的问题。（板书：超出平均数的部分=不到平均数的部分）

应用练习（智慧教室）：有位同学投了三次篮，但是周老师忘记统计他的第三次成绩了，可是我知道他的投篮平均个数是6，你猜猜他第三次投篮几个？四人小组讨论。

【设计意图：让学生动手、动脑，然后解决问题，极大地激发了学生探索的热情。】

三、精练——实践运用，解决问题

1.李强所在的快乐篮球队，队员的平均身高是160厘米。李强身高一定是160厘米吗？

【设计意图：数学就是从生活中来到生活中去，让学生理解平均数的含义，并发现数学在生活中的广泛应用。体会平均数和平均分不是相同概念。】

2.情境辨识：冬冬身高140厘米，他想到小池塘游泳，池塘的平均水深110厘米，他去游泳有危险吗？

师：平均数它反映的是整体水平，它会掩盖掉很多信息，同学们要学会明确的判断。

【设计意图：深化了学生对“平均数”概念的理解，让学生体验了事件发生的可能性，提升他们数学交流的能力。】

3.世界卫生组织发布了2015年版《世界卫生统计》报告。报告指出，从总体上看，截止到2013年，全世界人口的寿命都较以往有所增加。中国在此次报告中的人口平均寿命为：男性74岁，女性77岁。有位老爷爷今年73岁，他看到这则信息后很紧张，你想对他说什么？有位老奶奶今年78岁，你想对她说什么？

四、巧结——课堂回顾，深化认识

师：同学们回顾一下本节课学习的内容，说说你有哪些收获？

师：学了平均数，老师送给大家一句人生哲理：人生一切行为，应以中庸为法则，既不可过分自我膨胀，也不宜过分自我矮化。