说理，让学生在交流中遇见学习的模样——以《小数乘整数》一课为例

文|罗鸣亮

数学学习的过程必然伴随着交流的过程。交流，既有利于切入问题的本质，促进对知识的理解；又启发学生学会用习惯的方式和节奏走进自己、走进他人、走进文本，在交流中学会学习，在学习中学会数学交流，最终通向数学知识的再经历、再创造。

但日常教学中，我们常见课堂中的数学交流往往由教师和学优生主导，多数学生缺少交流分享的机会，学生之间也较少产生互动，越来越习惯于“听”数学，而不是“说”数学、“学”数学。以《小数乘整数》一课为例，如何帮助学生从被动的“听”数学转向主动的“说”数学、“学”数学？帮助学生学会用习惯的方式和节奏主动融入到交流中，构造属于自己的学习呢？

一、在交流中看见自己

如果学习只是不断地听、不断地输入各种知识与观点，一旦没有使用，转身就会忘记。这样的学习远离了真实，远离了直面探究、升级思维等过程。而不管何种学习，都应启发学生走进自己，主动思考。我们知道，学生天生好质疑。因此，好的质疑能引发学生产生好奇，主动走进已有的认知经验，结合问题审视自我，批判性地与已有的经验进行对话，进而在迁移、组合、链接经验中形成自己的思考，产生可能的思想蜕变。

【教学片断一】

师：学过整数乘法了吗？

（课件：30×4＝？）

生：等于120。

（课件0.3×4＝？）

生：（教师把话筒递给两位学生，都回答）1.2。

师：奇怪了，小数乘整数学过了吗？没学过你们怎么都会呀？

怎么启发学生看见自己？认识自己？教学借由两个式子“30×4＝？”“0.3×4＝？”引发质疑：没学过怎么都会呀？暴露出学生的现有水平，使学生站在已有的水平上与内在的自我进行对话，辨别已有的经验，把自身的学习经验与知识基础联系起来，直面需要解决的问题，以自己的方式展开对问题的解决与创造。有的从加法的意义来迁移，提出“把4个0.3加起来，不用乘法用加法”；有的根据两个乘法算式中乘数的关系来推理积的关系，认为“0.3是30的，30×4＝120，所以用120÷100，把它的小数点向左挪两位，等于1.2，0.3×4＝1.2”；也有的将小数乘法转化为整数乘法来计算，建议“先把0.3看成3，直接3×4＝12，3÷10＝0.3，所以12÷10＝1.2”……

在这个过程中，学生在与自我的交流中产生独有的思考，迁移已有的知识经验解决问题，与未知展开说理，使得学习从看见已有的“自己”开始，于跃向未来的“自我”探索中真正展开。

二、在交流中听见他人

每个人的成长不应该是一条孤独的航线，而是与他人的思考用各种方式交织在一起。学会看见他人的思考，学会一群人一起合作解决问题，或许才是学习的关键。因此，教学不仅要启发学生走进自己，输出、展示自己，更要给学生拥有“听见”他人思考的机会。教学借助淘气的想法（如图1），引发学生在“淘气画的图表示的是哪一个算式的计算道理呢”这一问题中，将思考外显，进入讨论与交流的学习状态。

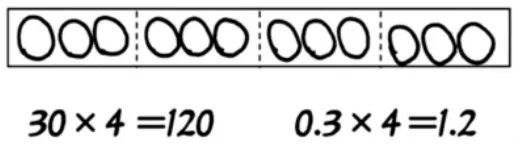
图1

【教学片断二】

生：我觉得是0.3×4＝1.2，因为一个○表示0.1，所以是0.3×4＝1.2。

生：一个○也可以表示10，我觉得是30×4＝120。

生：我认为两个都不是。一个○表示1，淘气的图表示的应该是3×4＝12。

生：我们小组认为都可以。一个○表示10，3个○表示30，4组就是30×4＝120。也可以一个○表示0.1，3个○表示0.3，4组就是0.3×4＝1.2。

生：这道题太多不确定因素了，我觉得每个人说的都有道理。因为每一个圈可以表示数字10，也可以代表0.1。

生：每一种都有可能，每一种都有道理，但我真的不知道淘气表示的是哪一种。

生：如果两种都是的话，那可能性就有无数种，可以是1，可以是2，可以是0.1，可以是0.2。

不同思考的交流中，产生了不同的意见，但也触发学生跳脱自己的视角，联系他人的思考，从更开阔的角度去洞察、去审视，进而提出“有无数种可能性”。此时，学生已然把自己置身于“与自己、与知识、与他人”的关系中，看见自己、也听见他人。他人的表达，触动学生与之进行内在对话，确认思考上不同之时，又兼容多样的思考。或产生质疑，或获得启示，进而使交流产生的力量不断生长，明晰淘气的图既可以表示“3个10×4＝12个10”，也可以表示“3个0.1×4＝12个0.1”。教学继而借助问题“淘气这个图还可以表示哪些算式的道理呢”启发学生进一步辩论，敞开自己的精神世界，同时接纳他人，最终获得理解和沟通，主动站在乘法意义的制高点，用系统的、整体的眼光看待和理解图中蕴含的深刻道理：可以表示3个任何数乘4，进而厘清小数乘整数和整数乘法的算理本质，一样都在数有多少个这样的计数单位。

说理课堂中的讨论交流，每个发言、每个观点都是一个连接点，沟通了学生的思考与交流。我们希望帮助每位学生不仅看见自己，更借助表达、讨论和交流等途径，实现人与人之间的网状连接，让每一位学生被“听见”。帮助学生不断地自我调整、自我完善，实现自我成长。

三、在交流中走进文本

文本的意义并不在文本本身，而在于阅读者与文本之间的相互遇见与影响。说理课堂中的学习，不仅引领学生与“人”对话，还启发学生与“文本”对话，知道如何与“文本”对话，如何透过表面文本的阅读思考和解决问题，如何提炼与表达自己的观点；更知道如何走进文本的深处，在交流中深化自己的思考，形成自己的认知方式。

“竖式中的4写在2的下面还是3的下面呢？”教学再次于学生的真困惑处驻足，并借助竖式文本（如图2），引发学生带着质疑，充分地透过文本中的两个竖式，深入到乘法算理中，将小数乘法与整数乘法联系在一起，深度的交流也得以充分地展开。有的联想小数加减法的竖式计算，认为4应对齐个位；有的则从整数乘法想起，提出可以把2.13看成213，先算213×4，结果再点小数点，所以赞成4和小数的末位对齐。学生各执己见，双方辩论不停，都认为虽然计算结果是一样的，但对方赞成的对齐方式改变了算式表示的意思。教师的适时介入，会引发学生产生怎样的交流呢？

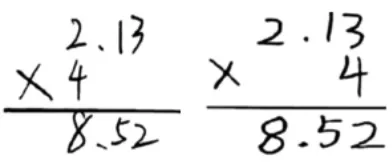
图2

【教学片断三】

师：还有没有第三种观点？

生：两个都对。第一个竖式的4可以看成4.00。

生：如果两个都对的话，平时老师还怎么改作业？

师：想不想知道淘气是怎么想的？淘气也发现，这两个答案都对。把2.13看成213来算，所以4写在3的下面有没有道理？

师：问题来了，想一想，2.13×4和2.13＋4中的4表示的意义一样吗？

生：不一样，加4是表示加上4个1，乘4表示4个2.13相加。

师：所以，4无论写在哪个数字下面，都可以表示有4个2相加，有4个0.1相加，又有4个0.03相加。

师：老师改作业怎么办呢？不着急，我们以前学过2130×4，这个竖式怎么列的？4写在哪个数字下面？

生：两个都可以，如果在3和0的中间画一条虚线，0就可以省略，得出积的时候再把0加上。

（出示课件如图3）

图3

生：所以4写在3的下面，这样更简便。

师：对，这样就把2130看成了213个10，所以4写在3的下面，算出852个10。

师：想一想，我们已经把2.13看成什么？

生：当成213来计算，算出852个0.01，所以把4写在3的下面。

师：对了，数位对齐可以，但为了方便以及和整数乘法统一，一般末位对齐。

“竖式中的4应该写在哪”这个话题中，又进一步为学生提供整体认识乘法的机会，在整数乘法和小数乘整数中搭建桥梁。从“竖式中的4应该写在哪”的纠结到“写哪都行”的统一，辩论的双方最终在说理中，深入到文本蕴含的思想与方法，不仅凸显出学生对乘法意义的感知、识别和领悟，更凸显出同伴互助交流的价值。在这其间，学生主动透过文本关联整数乘法与小数乘法，也主动关联自己与文本、与他人的思考，相互补充、相互质疑。既拓宽原有经验的边界，更使原有的零碎知识变成一个相互关联、相互统一的整体，深刻体会整数乘法与小数乘整数算理的一致性的同时，发展自己。

四、在交流中创造学习

学习的过程是一个发现的过程，是一个创造的过程。我们希望，说理课堂上的交流，能把注意力的聚焦分配给每一个学生，撬动学生透过问题，带着每一次真实的思考，通过每一次真诚的交流，重新认识自己，搭建起与文本、与他人链接的桥梁，不仅思考现在，更能拥抱未来，推动自己去往更远、更广阔的天地，创造属于自己的学习。

【教学片断四】

师：通过这节课的学习，你的感受有哪些？

生：换一个角度想问题，就会有不一样的结果。

生：有辩论的感受，有抢话筒的感受。

生：想问题要从多方面思考。

生：这次辩论让我懂得，要多思考对方的角度是否是对的，不能一意孤行，只想着自己的角度。

生：这次辩论让我明白看问题不能只看一个角度，要从多方面去看。

……

通过课尾的学习感受，我们可以看到学生于交流中所体会到的力量，既往深处发现自己，又不断用他人的思考映照自我，进而认识到个体的独特性及团队的互助性，领悟多维度思考带来的魅力。我想这节课的学习，学生所收获的已不局限于小数乘整数的答案，不局限于知识上的生长，更多的是展开了关于自我的真成长、学习的真思考、思想的真启迪。

所以，交流是什么？什么样的交流才能给课堂上的每一个个体带来满足感？我想，当学生借由旧经验看到“自己”、表达“自己”，开始解惑的时候；当学生追寻知识道理的过程中越过自己、听见“他人”，最终达成共识的时候；当学生把自己融入文本思想中，走进“文本”，创造新经验的时候；当学生走进多元的交流，把自己放到“关系”中，更好地认识自我、发展自我的时候……学习早已潜入其中，充满了意外的发现和共同的探索。