基于VF-DW-DFN的锂离子电池剩余寿命预测

锂离子电池因其低自放电率、高能量密度、长使用寿命等优点而作为主要电源应用在各类工业领域，包括移动电话、电动汽车、储能系统等

。然而，锂离子电池的失效会导致设备性能退化、维护成本增加，甚至造成灾难性的设备故障问题

。因此，锂离子电池的运行状态，包括健康状态(state of health，SOH)和剩余寿命(remaining useful life，RUL)等，对于工业设备和系统的正常运行十分重要，必须开发先进的算法来准确有效地预测锂离子电池的剩余寿命，保障设备运行的安全性和可靠性，实现工业系统的预测性维护。

现有的锂离子电池RUL 预测方法主要分为基于模型的方法和基于数据驱动的方法。基于模型的方法主要有电化学模型法、等效电路模型法、经验退化模型法。电化学模型法

是通过电池内部化学反应机理建立相应的代数或微分方程来进行寿命预测，准确性高，但模型参数易受温度等因素影响，因而参数辨识困难，建模过程复杂；等效电路模型法

利用电路分析建立电池的等效数学模型，考虑了电池老化机制，但模型建立依赖于阻抗等在实际中难以获取的数据；经验退化模型法主要基于电池容量的指数模型与滤波算法相结合来进行RUL 预测。Chang 等

提出了一种无迹卡尔曼滤波与双指数模型相结合的RUL 预测方法。Wei 等

使用混合指数模型和粒子滤波预测电池RUL。然而，经验退化模型仅能近似表达电池退化过程，且预测性能受限于相结合的滤波算法。

近年来，数据驱动的故障预测方法在电池RUL 预测应用中显示出了巨大的前景

。诸如支持向量机(support vector machine，SVM)

、相关向量机(relevent vector machine，RVM)

和人工神经网络(artificial neural network，ANN)

等方法已经用于锂离子电池的RUL 预测，这类方法无需了解复杂的电池退化机理，避免了模型自身准确性对预测精度的影响，但以上方法大多为单一预测模型，存在泛化性不强、精度不高等问题，因此融合运用信号处理、多模型混合、集成学习等方法成为了当前电池寿命预测研究的新趋势。陈铮等

通过对锂电池充电数据进行特征提取和降维，采用径向基神经网络实现电池RUL 估计。Chen等

结合相空间重构，利用SVM 和误差补偿提高了锂离子电池RUL预测精度。Xue等

融合自适应无迹卡尔曼滤波、SVM 与遗传算法对锂离子电池进行剩余寿命预测。然而上述方法大多为浅层模型，特征学习能力有限，存在长期寿命预测精度不高的问题。

除了上述数据驱动的RUL 预测方法，深度神经网络作为一类典型的数据驱动方法，能够从特征数据中自适应地提取关键信息，实现数据建模，因而也开始被广泛应用于锂离子电池RUL预测领域。Babu 等

采用卷积神经网络(convolutional neural network，CNN)提取原始数据的深层特征，并结合多层感知机进行RUL 估计。Ma 等

利用循环神经网络(recurrent neural network，RNN)中的长短时记忆网络(long short-term memory，LSTM)的长期时序预测能力，结合虚假近邻算法进行锂离子电池RUL预测。易灵芝等

基于门控循环单元(gated recurrent unit，GRU)提出了EEMD-GSGRU模型用于不同的锂电池RUL 预测。然而，CNN 的性能依赖于卷积核的设置，且随着网络层数的加深，网络训练难度加大，同时容易产生过拟合；在RNN 及其变体中，当电池数据噪声较多或数据量较小时，通常会出现欠拟合现象。此外，实际电池使用过程中存在容量再生现象，导致容量衰减过程频繁波动，基于原始RNN 的预测方法容易失效

，且工况条件不同带来的随机噪声干扰也会造成电池工作状态波动起伏，电池退化过程在上述因素的共同作用下表现出明显的非平稳、非线性特性，如果直接使用原始退化数据进行建模，会使得电池RUL 预测更为困难。

针对上述锂离子电池退化过程中存在的多种复杂特性导致单一数据驱动方法预测精度低、泛化性能差等问题，本文提出融合变分滤波、数据规整与深度融合网络的数据驱动方法(VF-DW-DFN)。该方法首先利用变分滤波(variational filtering，VF)重构原始电池容量退化序列，滤除噪声干扰，得到相对平稳的特征序列。然后通过最优嵌入(optimal embedding，OE)法构造滑窗特征输入，实现数据规整(data wrapping，DW)。最后融合时间卷积网络(temporal convolutional network，TCN)、扩张门控循环单元(dilated gated recurrent unit，DGRU)和自回归模型建立有效的深度融合网络(deep fusion network，DFN)，实现电池RUL的精准预测。

1 电池的SOH与RUL定义

本文采用3种常用的评价指标来定量评估电池剩余寿命预测方法的预测性能，分别为均方根误差(root mean square error，RMSE)、平均绝对误差(mean absolute error，MAE)、绝对误差(absolute error，AE)，计算公式分别如下：

首先对电池容量退化数据进行VF 滤波去噪。通过对VF 算法参数多次寻优，设定

为5，

为2000，

为10

，

为0.001，得到最终的电池容量VF 滤波结果如图6 所示。与原始容量曲线相比，滤波处理后的曲线变化更为平稳，退化趋势相对平滑，既保留了原始容量数据的主体退化特征，又减小了容量再生和随机噪声干扰的影响，使得电池容量的变化模式更为明晰，有利于DFN 网络模型的退化特征辨识与建模，提升预测精度。

式中，y、a、b和x分别代表变量的回归结果，时间趋势、截距以及年份。通常地，当a>0时，表明变量y呈增加的趋势，反之则呈减少的趋势。

根据脱氧乌头碱的加热研究结果表明，由于其与乌头碱都为C19二萜生物碱，结构相似，故二者的水解途径类似，脱氧乌头碱在加热的过程中，主要有去氧乌头次碱、去氧乌头原碱和焦去氧乌头碱这几种产物，在此过程中，脱氧乌头碱易先水解为去氧乌头次碱，再分解为去氧乌头原碱，该成分没有紫外吸收，在色谱图中没有显示，在质谱图中能够检测到。

4）信息化模型在各专业交流上具有非常大的优势，只要利用建筑构件数据的统一标准化，我们就可以多专业同时交流讨论保护方案的相关问题和解决方案，也减少了每个专业各建一套信息模型的人力物力的浪费和信息的不精准等造成的新的困难。

电池RUL预测过程如图1所示，其中

为预测滑窗大小。根据现有文献，当电池循环容量衰减至初始容量值的70%～80%时，认为电池到达寿命终点

。因此，精准的电池容量预测是实现电池RUL预测的关键。

基金项目：湖南省教改项目“认知学徒制在应用心理学实践教学中的应用和研究”（2013）；湖南中医药大学校级教改项目“基于随机通达教学理论的应用心理学教学改革研究与应用”（2015）

2 基于VF-DW-DFN的RUL预测

①构造关于电池容量退化序列

(

)的非限制性变分问题：

2.1 输入序列变分滤波

本文提出的深度融合网络(DFN)结构如图3 所示。DFN 主要由输入层、TCN 卷积层、DGRU 循环层、全连接层、自回归线性层、预测输出组成，其中，TCN 卷积层融合了因果卷积

、扩张卷积

、残差学习

的优点，在时间维度进行卷积操作，用于提取输入电池数据中的深层次退化特征，同时缓解原始数据中存在的噪声干扰，保证网络的整体稳定性；DGRU循环层是一种层级时序扩张和跳跃连接的多层门控结构

，能够应对RNN 中梯度反向传播困难的问题，处理时序关系，记忆长时信息；自回归线性层可以克服电池容量退化序列尺度不断以非周期性方式变化导致神经网络模型产生的输出迟滞反应

，提高整体网络的鲁棒性。

中国进入新时代，中国酒业正在进入承上启下的变革时代。当前人们日益增长的美好生活需要更加广泛和多元化，也要求白酒产业链上的每一个环节都要充分了解消费者的新需求、新变化，把握消费新趋势，并对市场做出积极应对。

本文提出的基于VF-DW-DFN的RUL预测总体框架如图2所示，主要包括输入序列VF、滑窗特征DW、DFN训练、电池RUL预测四个主要部分。

1.4 叶果比不合理 一些果农贪图高产，留果量过大，叶果比失调（有些叶果比值还不到3），造成树体负载过大（亩产 2 000～3 000 kg），果实贪青晚熟，引起萎蔫。

2.2 滑窗特征数据规整

最优嵌入(OE)法

是一种用于估计时间序列嵌入维数的方法，本文基于经过VF 算法后的电池退化容量数据，采用OE 算法构造预测模型的滑窗容量输入，实现数据规整，减少信息损失。

定义向量

表示变分滤波后的电池退化容量时间序列：

2.3 深度融合网络构建与训练

本文提出的(VF)法主要由变分模态分解(variational mode decomposition，VMD)

和Pearson相关系数分析构成，通过采用VMD 将输入序列非递归地分解为多个不同频率特征的模态分量，然后利用Pearson相关系数计算各分量与原始序列的相关度，并根据阈值法则筛选分量，最后重组相关度高的分量得到重构序列，实现输入序列的变分滤波，消除容量再生和随机噪声干扰带来的非平稳性影响。VF算法实现步骤如下。

你走了，不要记恨宿舍的弟兄们，他们也是为你好，万一你走投无路，出了事，我们哥几个还要掏钱给你买花圈，最好不会这样，你给我们省顿早餐吧。

本文使用均方误差(mean squared error，MSE)损失函数用于模型训练过程的优化，定义损失函数如下：

参考GenBank中乙型脑炎病毒JaOArS982 (NC001437) C基因序列，设计C基因对pET42b载体的特异性引物，引物由武汉天一辉远生物科技有限公司进行合成。如表1 (下划线为加入酶切位点：Nde I/Xho I)。

电池RUL 一般定义为：在特定工况条件下，电池的运行状态衰减到设定的失效阈值所经历的充放电循环次数，其中电池的容量状态是最为常用的阈值指标。用于RUL 预测的起点容量值称为监测终点阈值(end of monitoring，EOM)，对应循环数

；寿命终点阈值(end of life，EOL)为电池失效时的容量值，对应循环数

，因此，电池RUL可具体定义为：

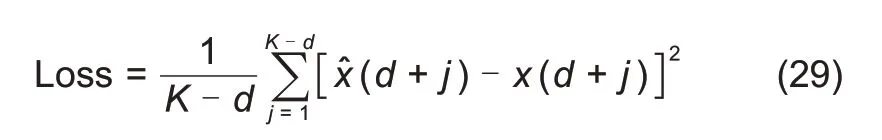
其中

̂(

+

)为第

+

个循环周期的预测值，

(

+

)为真实值。在训练过程中，选择Adam 算法反向传播更新模型参数，当模型损失达到预定义的收敛阈值后停止训练。最后，将滑窗测试集输入训练完成的DFN 模型，由第1 节中RUL 的计算定义式(2)，即可实现锂离子电池的剩余寿命预测。

3 实验验证

3.1 实验数据说明

本文使用的锂离子电池退化数据来自NASA PCoE 研究中心

。电池数据采集自NASA 18650钴酸锂锂离子电池故障预测实验台，编号为B5、B6、B7，额定容量为2 Ah。电池在室温下运行于3 种不同的工作模式：充电、放电和阻抗模式，首先以1.5 A恒流状态充电，直到电压达到4.2 V，然后以恒压状态继续充电，当充电电流降至20 mA时终止充电。在放电阶段，电池以2.0 A 的恒定电流放电，使电池电压分别降至2.7、2.5、2.2 V。重复上述充放电过程直到电池容量衰减至失效阈值，即额定容量的70%(1.4 Ah)。图5 给出了锂离子电池放电容量退化过程曲线，由图5可看出，由于放电深度不同，各电池的退化速率也不同，且随着循环次数的增加，电池退化容量不仅具有明显的下降趋势，而且容量再生现象和随机噪声干扰明显，电池状态波动频繁，退化数据呈现出显著的非平稳性和非线性。

3.2 评价指标

电池的SOH 代表在每一个充放电循环的电池健康状态，是表征电池老化程度的健康指标。在本文中，采用容量比定义SOH。定义第

次循环的SOH(

)为：

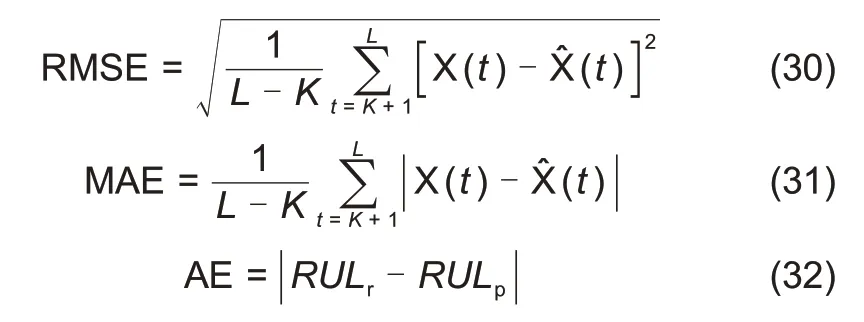
其中RUL

,RUL

分别表示电池的实际RUL 和模型预测RUL，X(

)、X̂(

)分别表示测试集的实际电池容量和模型预测电池容量。对于上述指标，RMSE、MAE、AE越小，模型预测性能越好。

3.3 电池容量数据滤波

其中

(0)表示初始容量，通常为电池的额定容量，

(

)是第

次充放电循环后的电池容量。

3.4 特征数据规整

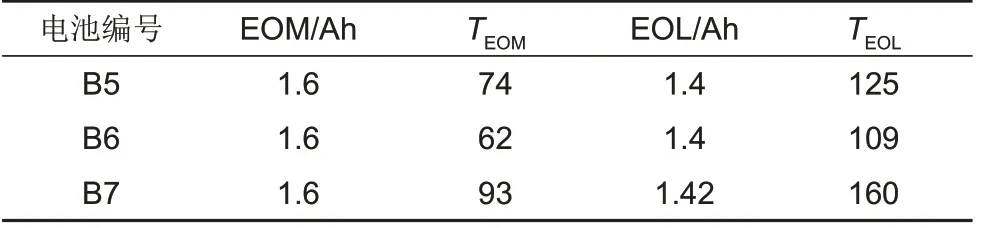
根据电池RUL的定义，设置电池B5、B6、B7的EOM 阈值为额定容量的80%，电池B5、B6 的EOL 阈值为额定容量的70%，B7 为71%

，得到各组电池的阈值设置见表1，并由

划分滤波后的各电池容量序列。

以电池B5 为例，滤波后的电池容量序列共有168 组数据，取前74 组为训练数据，后94 组为测试数据，根据2.2 节的数据规整算法计算滤波后各电池容量序列的

1 值、确定最优嵌入维数、构造滑窗容量特征集，由当前时刻的

维滑窗容量输入预测下一时刻的容量输出值。各电池容量序列

1值大小变化如图7所示。随着嵌入维数的增加，

1值逐渐趋于稳定的饱和值。此外，嵌入维数选取过小则无法提取到足够的退化信息，导致滑窗信息损失，而选取过大会造成可构造的训练样本数过少，导致过拟合，因而综合考虑以上选取准则确定最优嵌入维数，得到各电池容量序列的最优滑窗大小设置为B5∶15，B6∶13，B7∶15，最后根据最优滑窗构造滑窗训练集和测试集，进行后续网络模型的训练与RUL预测。

3.5 RUL预测结果与分析

DFN网络模型的训练参数设置如表2所示。模型训练完成后，根据滑窗测试集得到最终的电池容量估计值，进而得到锂离子电池的RUL预测结果。

表3和图8给出了本文的锂离子电池RUL预测结果，B5 电池的RUL AE 为1，B6 电池的RUL AE为1，B7 电池的RUL AE 为2，基于VF-DW-DFN的方法可以准确预测不同电池容量的退化趋势，并对容量再生和随机噪声干扰有较好的适应性。因而，实验结果表明本文所提方法的估计误差小，RUL预测精度高，泛化能力强，能够对锂离子电池的剩余寿命进行准确预测。

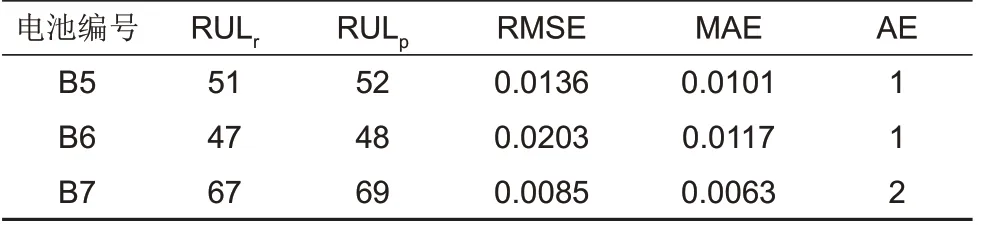
图9 和表4 给出了不同滑窗大小选择下VFDW-DFN的预测结果对比。由图表可知，选择最优滑窗时，在各个电池数据集上的预测结果的平均RMSE 为0.0141，平均MAE 为0.0094，平均AE小于2；选取过小滑窗5 时，预测结果的平均RMSE 为0.0269，平均MAE 为0.0231，平均AE为4；选取过大滑窗30时，预测结果的平均RMSE为0.0413，平均MAE 为0.0382，平均AE 为10；在B7 中，由于预测间隔较长，滑窗过小和过大都无法得到有效的RUL预测。因此，通过OE算法选择的最优滑窗在各个电池数据集上取得的预测性能最好，而滑窗选取过小或过大都会导致RUL 预测误差变大，性能下降，甚至造成预测失效。

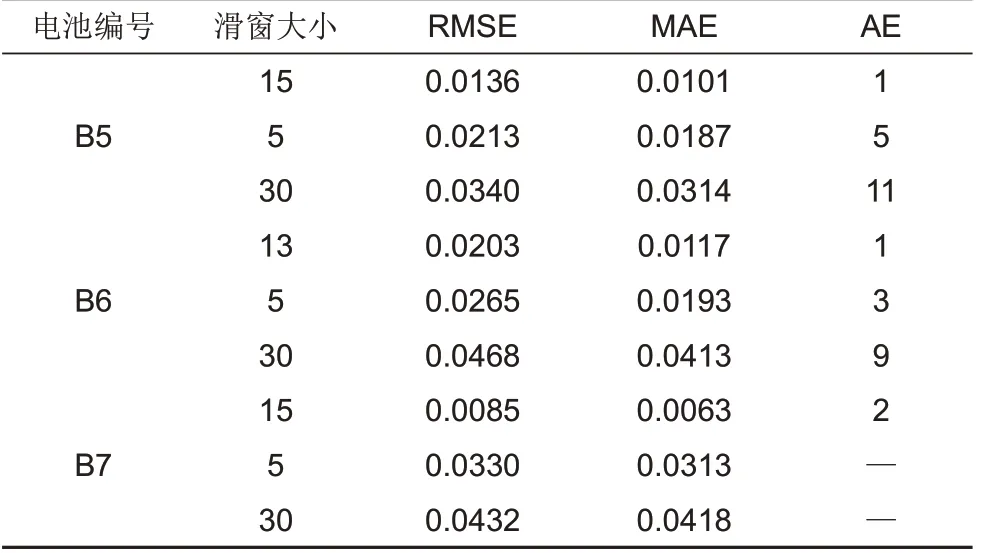
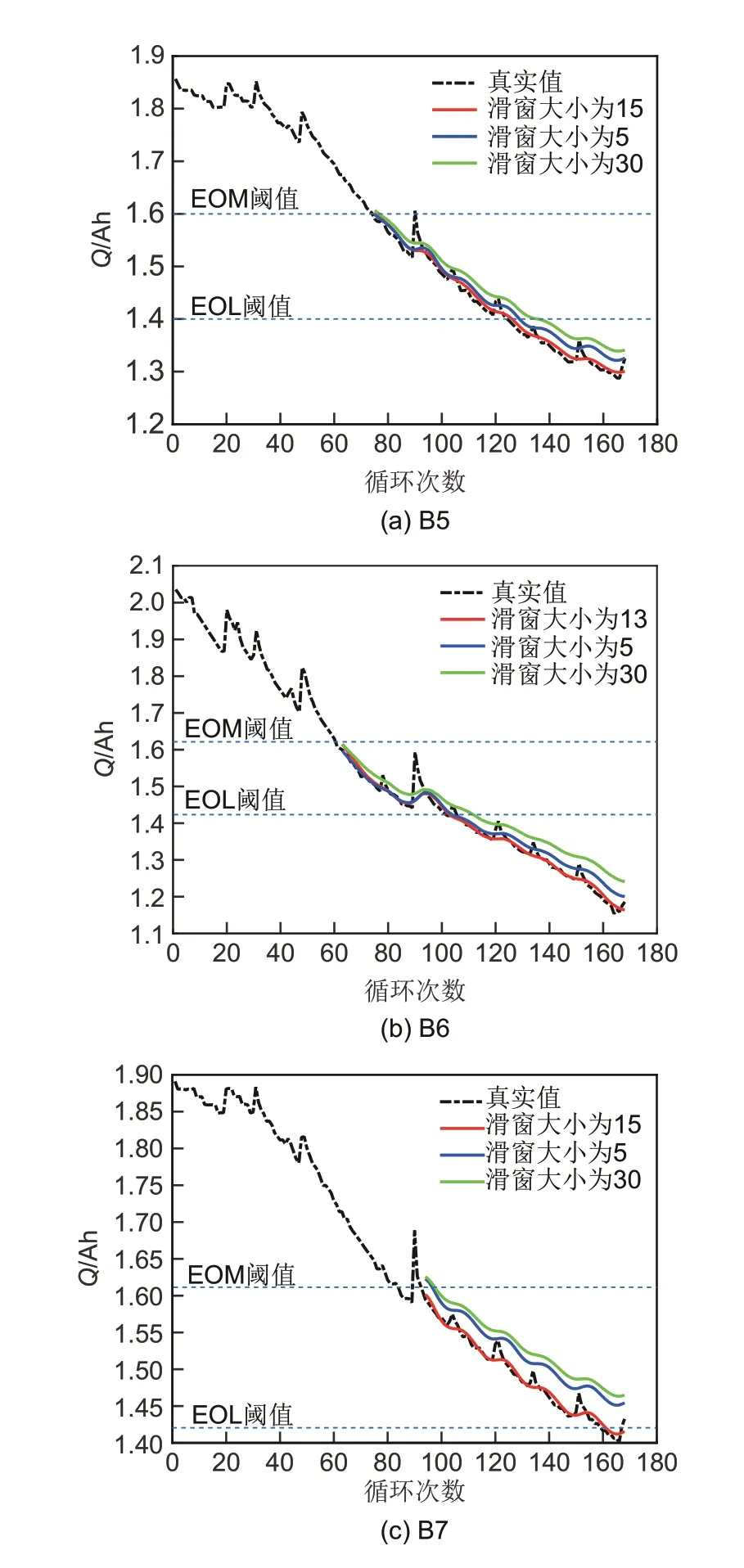
表5 和图10 为相同实验条件下，VF-DWDFN，VF-DW-SVM 和VF-DW-LSTM 三种方法的预测性能对比。由图表可知，相比于VF-DW-SVM和VF-DW-LSTM，基于VF-DW-DFN 方法的平均预测RMSE分别降低了63.4%、65.0%，平均预测MAE 分别降低了73.4%、74.7%。VF-DW-DFN 方法的平均预测AE 小于2，而VF-DW-SVM 和VFDW-LSTM 的平均预测AE 均大于10，说明SVM、LSTM等传统数据驱动方法容易受电池容量退化数据非平稳、非线性特性的影响而产生较大的预测偏离，而VF-DW-DFN方法能够克服上述因素带来的影响，有效辨识退化趋势，降低预测误差，提高预测鲁棒性。

3.6 方法对比

本文还进一步将VF-DW-DFN方法与其他文献中的方法进行对比，包括AUKF-GASVR

、CNNLSTM

、BCT-RVM

、HA-FOSELM

等 方 法，RUL预测性能对比如表6所示。对比结果表明，本文提出的方法在不同电池数据集上的综合表现优于对比的方法。VF-DW-DFN 通过融合不同方法的优点，得到的预测误差最低、精度最高、泛化性最好，表明该方法能够针对不同工况条件下电池退化序列的特点自适应地学习到相应的动态变化模式，提高了锂离子电池寿命预测的准确性和泛化性。

4 结 论

锂离子电池作为重要的工业故障预测与健康管理对象，广泛存在非线性、非平稳等工业RUL 预测共通问题。本文围绕锂离子电池RUL预测，提出了基于变分滤波、数据规整和深度融合网络的数据驱动融合方法，进而形成了一类基于VF-DW-DFN的RUL 预测方法。为了验证本文所提方法的有效性，针对锂离子电池RUL 预测数据集，利用变分滤波法对电池容量退化序列进行滤波去噪，缓解了电池容量再生和随机噪声干扰带来的非平稳性影响。采用数据规整构造滑窗特征集，减小了主观人为性造成的特征信息损失，提高了数据利用率。设计了DFN 网络，融合了TCN、DGRU、自回归等子模型的优点，实现了对非线性电池退化序列的有效建模。在3种电池数据集上RUL预测的RMSE分别为0.0136、0.0203、0.0085，AE 分别为1、1、2，平均RMSE 在1.5%以内，平均AE 小于2，实验结果表明本文所提方法相较于现有方法，可以有效提高锂离子电池RUL预测的准确性与泛化性。

未来的工作将重点关注于：①进一步优化VF算法和DFN 网络，实现算法和模型参数的自适应选择；②结合概率密度函数进行电池RUL 的不确定度预测。

[1] 梁新成,张勉,黄国钧.基于BMS的锂离子电池建模方法综述[J].储能科学与技术,2020,9(6):1933-1939.LIANG X C, ZHANG M, HUANG G J. Review on lithium-ion battery modeling methods based on BMS[J]. Energy Storage Science and Technology,2020,9(6):1933-1939.

[2] OMARIBA Z B, ZHANG L J, SUN D B. Review on health management system for lithium-ion batteries of electric vehicles[J].Electronics,2018,7:72.

[3] 袁烨,张永,丁汉.工业人工智能的关键技术及其在预测性维护中的应用现状[J].自动化学报,2020,46(10):2013-2030.YUAN Y, ZHANG Y, DING H. Research on key technology of industrial artificial intelligence and its application in predictive maintenance[J].Acta Automatica Sinica,2020,46(10):2013-2030.

[4] ZHANG W J. A review of the electrochemical performance of alloy anodes for lithium-ion batteries[J]. Journal of Power Sources,2011,196(1):13-24.

[5] 康鑫, 时玮, 陈洪涛. 基于锂离子电池简化电化学模型的参数辨识[J].储能科学与技术,2020,9(3):969-978.KANG X, SHI W, CHEN H T. Parameter identification based on simplified electrochemical model of lithium ion battery[J]. Energy Storage Science and Technology,2020,9(3):969-978.

[6] 朱奕楠, 吕桃林, 赵芝芸, 等. 基于并行卡尔曼滤波器的锂离子电池荷电状态估计[J].储能科学与技术,2021,10(6):2352-2362.ZHU Y N, LÜ T L, ZHAO Z Y, et al. State of charge estimation of lithium ion battery based on parallel Kalman filter[J]. Energy Storage Science and Technology,2021,10(6):2352-2362.

[7] 任璞, 王顺利, 何明芳, 等. 基于内阻增加和容量衰减双重标定的锂电池健康状态评估[J].储能科学与技术,2021,10(2):738-743.REN P,WANG S L,HE M F,et al.State of health estimation of Liion battery based on dual calibration of internal resistance increasing and capacity fading[J]. Energy Storage Science and Technology,2021,10(2):738-743.

[8] CHANG Y, FANG H J, ZHANG Y. A new hybrid method for the prediction of the remaining useful life of a lithium-ion battery[J].Applied Energy,2017,206:1564-1578.

[9] WEI J W, DONG G Z, CHEN Z H. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression[J]. IEEE Transactions on Industrial Electronics,2018,65(7):5634-5643.

[10]陈翌, 白云飞, 何瑛. 数据驱动的锂电池健康状态估算方法比较[J].储能科学与技术,2019,8(6):1204-1210.CHEN Y, BAI Y F, HE Y. Comparison of data-driven lithium battery state of health estimation methods[J]. Energy Storage Science and Technology,2019,8(6):1204-1210.

[11]SEVERSON K A,ATTIA P M, JIN N, et al. Data-driven prediction of battery cycle life before capacity degradation[J]. Nature Energy,2019,4(5):383-391.

[12]PATIL M A, TAGADE P, HARIHARAN K S, et al. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation[J]. Applied Energy, 2015,159:285-297.

[13]CHANG Y, FANG H J. A hybrid prognostic method for system degradation based on particle filter and relevance vector machine[J].Reliability Engineering&System Safety,2019,186:51-63.

[14]李练兵, 李思佳, 李洁, 等. 基于差分电压和Elman 神经网络的锂离子电池RUL预测方法[J].储能科学与技术,2021,10(6):2373-2384.LI L B, LI S J, LI J, et al. RUL prediction of lithium-ion battery based on differential voltage and Elman neural network[J]. Energy Storage Science and Technology,2021,10(6):2373-2384.

[15]陈峥, 李磊磊, 舒星, 等. 基于特征处理与径向基神经网络的锂电池剩余容量估算方法[J].储能科学与技术,2021,10(1):261-270.CHEN Z, LI L L, SHU X, et al. Efficient remaining capacity estimation method for LIB based on feature processing and the RBF neural network[J]. Energy Storage Science and Technology,2021,10(1):261-270.

[16]CHEN L, ZHANG Y, ZHENG Y, et al. Remaining useful life prediction of lithium-ion battery with optimal input sequence selection and error compensation[J]. Neurocomputing, 2020,414:245-254.

[17]XUE Z W, ZHANG Y, CHENG C, et al. Remaining useful life prediction of lithium-ion batteries with adaptive unscented Kalman filter and optimized support vector regression[J].Neurocomputing,2020,376:95-102.

[18]SATEESH BABU G, ZHAO P L, LI X L. Deep convolutional neural network based regression approach for estimation of remaining useful life[C]//Database Systems for Advanced Applications,2016.

[19]MA G J, ZHANG Y, CHENG C, et al. Remaining useful life prediction of lithium-ion batteries based on false nearest neighbors and a hybrid neural network[J]. Applied Energy, 2019,253:113626.

[20]易灵芝, 张宗光, 范朝冬, 等. 基于EEMD-GSGRU 的锂电池寿命预测[J].储能科学与技术,2020,9(5):1566-1573.YI L Z, ZHANG Z G, FAN C D, et al. Life prediction of lithium battery based on EEMD-GSGRU[J]. Energy Storage Science and Technology,2020,9(5):1566-1573.

[21]QIN T C, ZENG S K, GUO J B, et al. A rest time-based prognostic framework for state of health estimation of lithium-ion batteries with regeneration phenomena[J]. Energies, 2016,9(11):896.

[22]DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014,62(3):531-544.

[23]BOYD S. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends®in Machine Learning,2010,3(1):1-122.

[24]CAO L Y. Practical method for determining the minimum embedding dimension of a scalar time series[J]. Physica D:Nonlinear Phenomena,1997,110(1/2):43-50.

[25]SHEN Z P, ZHANG Y M, LU J W, et al. SeriesNet: A generative time series forecasting model[C]//2018 International Joint Conference on Neural Networks (IJCNN). July 8-13, 2018, Rio de Janeiro,Brazil.IEEE,2018:1-8.

[26]LEA C, FLYNN M D, VIDAL R, et al. Temporal convolutional networks for action segmentation and detection[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. July 21-26,2017,Honolulu,HI,USA.IEEE,2017:1003-1012.

[27]HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. June 27-30, 2016, Las Vegas,NV,USA.IEEE,2016:770-778.

[28]CHANG S Y, ZHANG Y, HAN W, et al. Dilated recurrent neural networks[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York, USA: Curran Associates Inc.,2017:76-86.

[29]LAI G K, CHANG W C, YANG Y M, et al. Modeling long- and short-term temporal patterns with deep neural networks[C]//SIGIR '18: The 41st International ACM SIGIR Conference on Research&Development in Information Retrieval.2018:95-104.

[30]SAHA B, GOEBEL K. Battery data set[R]. NASA Ames Prognostics Data Repository,2007.

[31]LIU D T, ZHOU J B, LIAO H T, et al.A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems,Man,and Cybernetics:Systems,2015,45(6):915-928.

[32]FAN J M, FAN J P, LIU F, et al.A novel machine learning method based approach for Li-ion battery prognostic and health management[J].IEEE Access,2019,7:160043-160061.