LMD 方法在滚动轴承故障诊断中的应用
徐少梁,徐 乐,郝 洁,魏语辰,杜煜坤
(江苏师范大学,江苏徐州 221116)
0 引言
近些年,伴随工业领域的多元化发展,制造业机械设备逐步向高精度、高效率、智能化方向迈进。为了提高机械设备作业效率,同时保证工作人员生命安全,需要研究人员在协调机械设备的生产高效性与运行稳定性方面给予科学的设计方案[1]。其中,滚动轴承作为旋转机械不可缺失的基础零件,经常由于装配不当、润滑不足、外界侵蚀等原因引起局部损伤。过多的损伤诱因以及恶劣的工作条件可能引发机械设备故障,从而降低生产效益[2]。为了提高旋转机械运行效率,同时保持工作环境的安全稳定,实现对滚动轴承实时监测与故障诊断的操作至关重要。基于现代工业状态监测技术的先进成果,滚动轴承故障诊断融合了电子科学、传感器技术、视频调解等新手段,实现对滚动轴承运行状态的实时监测和数据采集分析。针对被提取数据的异常信息进行实时诊断,甚至可以达到预估设备零件未来运行状态的能力[3],进一步实现旋转机械在工作过程中保持良好稳定性且发挥出自身最大效能的预期。
1 局部均值分解方法
1.1 LMD 方法提出的背景
发生故障的滚动轴承会产生非线性、非平稳的调制信号,因此使用合理的方法分解并提取故障信号是滚动轴承故障诊断的关键。在LMD(Local Mean Decomposition,局部均值分解)方法提出之前,以往的信号分解方法并不能针对上述调制信号的特点而采取有效的改进措施,LMD 的提出对处理非线性非平稳信号过程中的端点效应、过包络、欠包络等问题提供了更优的解决方案[4]。LMD 算法是由信号驱动的自适应非参数方法,具有较强的鲁棒性局部均值分解,有助于提高提取有效信息的准确性[5]。LMD 在对非平稳信号的分析上有独特的优势,LMD 的端点效应远小于EMD,使信号在分解后能更完整地携带信息。同时,LMD 相较于EMD 的算法迭代次数更少,整个数据段的干扰等级更轻,因此LMD 在处理信号完整性、弱化端点效应等方面相较于EMD 的处理结果具有更高精度[6]。
1.2 LMD 方法及分解原理
LMD 方法本质上是将原始信号由多分量形式调解为多个PF 量积。其中PF 分量的组成部分是包络信号和纯调频信号的乘积,在此基础上通过迭代方法循环处理最终得到全部的PF分量,其分解步骤如下:
(1)设x(t)为原始信号,得到x(t)上的局域极值点ni,并计算局域极值ni和ni+1的平均值mi:

利用直线将mi构成的坐标连接,对折线光滑处理后得到局部均值函数m11(t)。
(2)利用局部极值点ni和ni+1,计算局域幅值ai:

采用同样的方法实现局域幅值点ai的连接,进行延伸后采用滑动平均法进行光滑处理,得到包络估计函数a11(t)。
(3)剩余信号h11(t)是通过在原始信号x(t)基础上分离对应的局域均值函数所得到的,即利用x(t)与处理过的m11(t)的差值获得。在得到h11(t)信号后利用包络估计函数a11(t)对其进行调解,具体过程如下:

理想状态下,纯调频信号的包络估计函数的值等于1。s11(t)若不满足该条件,则将s11(t)视为初始值并重复上述步骤直到s1n(t)(n=1,2,3…)是纯调频信号:

理论上迭代终止条件为:

(4)利用包络估计函数相乘,结果得到包络信号:
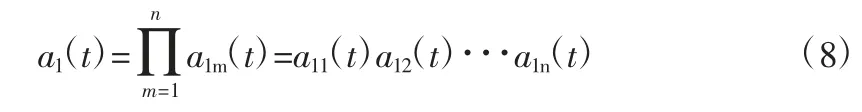
(5)通过公式计算可以近似得到的两个信号分别为纯调频信号s1n(t)和包络信号a1(t),将两个量相乘便可以得到x(t)的第一个PF 分量,公式表示如下:

(6)将原始信号x(t)与第一次得到分量PF1作差,得到从原始信号中分离出的新的信号u1(t)。将u1(t)作为新的初始数据重复上述步骤,直到uk(t)为单调函数,其迭代过程如下:
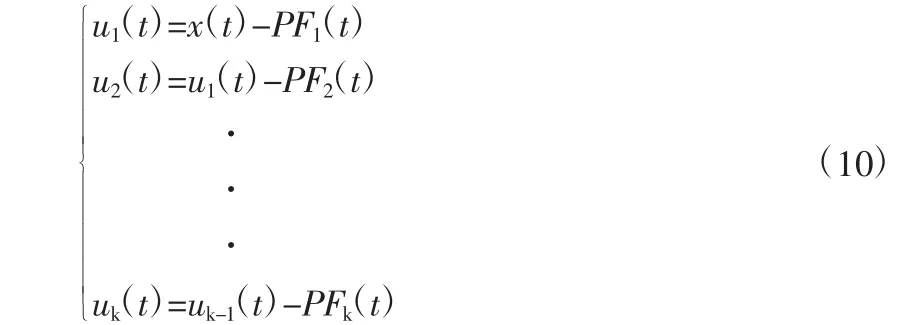
(7)将得到的每一个分量PFk(t)与信号余量uk(t)相加,最终实现对原始信号的重新构建:

2 LMD 方法在滚动轴承故障诊断中的应用与改进
滚动轴承产生故障时会造成一定程度的振动,振动引起的信号具有多分量调幅、调频等特点,且故障特征频率会随着轴承转速的变化而发生改变。为了在滚动轴承故障之前完成故障诊断并实现滚动轴承的检修,采用LMD 方法对滚动轴承振动信号进行分析和处理具有较强的优势。
2.1 LMD 方法在滚动轴承故障诊断中的应用
在使用LMD 方法对滚动轴承进行故障诊断前需要明白内圈、外圈、滚动体是构成滚动轴承结构体的主要部分。当这些关键的部位发生故障时,其振动信号会产生更为明显的冲击周期性变化[7]。通过对采样得到的有效数据给予合理判断,可以为接下来的故障分析提供数据支持。针对滚动轴承原始信号的数据检测,需要使用合理的信号采集方法,避免因所获原始信号的数据不准确性而造成对计算结果的不良影响。采用LMD 方法将原始信号分解成多个单分量调制信号之和的形式,再对得到的单分量振动信号的瞬时幅值进行快速傅里叶变换,通过以上操作可以得到与之对应的故障特征频率。这些通过FFT 变换得到的故障特征频率具有明显的辨识度并构成了具有有效信息的信号图样。包络谱在对应的故障特征频率处会以谱峰的形式表现出来。利用这一特点进行对瞬时幅值的包络谱分析,根据其转频f及其对应的幅值A 的线谱来判断滚动轴承发生故障的位置,进而实现对滚动轴承的诊断。
2.2 LMD 方法在滚动轴承故障诊断中的改进
随着LMD 方法在滚动轴承故障诊断中的应用和普及,LMD方法产生的端点效应、故障弱信号难以提取、PF 分量模态混叠等缺点也暴露出来。
为了解决这些问题,近年来研究学者对LMD 方法在振动信号领域进行了方法上的改进。杨德昌等人[8]在改进LMD 端点效应过程中采用了镜像延拓法有效减小信号采集的误差,并利用插值法优化了局部均值函数和局部包络函数信息。为了加强其局部均值分解鲁棒性,杨德昌等人在原始算法上设置了极值跨度和信号能量,这些改进措施有效提高了信号采集的准确性,避免了计算过程中的端点效应现象和负频率现象;李琳等人[9]提出一种基于梯度变化的端点效应抑制方法,该方法通过搜索原始信号的所有极值点对应的幅值判断包络线变化趋势,进一步判断包络线断点处发散状态进行包络拟合,改进后的LMD 分解方法有效解决了滚动轴承故障诊断中端点效应带来的计算精度不高的弊端;陈长征等人[10]在LMD 算法基础上引入互相关系数和峭度值2 个参数,分别判断随机信号的关联程度和振动信号的高斯性能(冲击成分的影响程),进而改善LMD 方法对滚动轴承故障弱信号的提取效果。这些改进措施让LMD 在该研究领域的应用得到了进一步的深入,对于增强旋转机械性能具有现实意义。
3 结语
以上介绍了滚动轴承零件在旋转机械中应用的广泛性,阐述了LMD 的算法流程和LMD 所具有的优点与创新性。将LMD和滚动轴承故障诊断相结合,引述了近年来研究人员针对LMD端点效应、PF 分量模态混叠、故障弱信号难提取等缺点所提出的改进方案。利用基于梯度变化的端点效应抑制方法、添加信号能量和极值跨度两个参数、引入互相关系数和峭度值等方法,提高了LMD 在滚动轴承振动信号的分解效率和故障诊断准确度。但与HHT 相同,LMD 同样利用信号固有包络特征来自适应地分解信号,仍然存在迭代终止条件和平滑跨度选取等问题。今后,针对如何提高LMD 运算效率和探索LMD 新的应用领域等问题还需要继续进行研究。

