气固流化床介尺度结构形成机制及过滤曳力模型研究进展

蒋鸣，周强，3

（1 西安交通大学化学工程与技术学院，陕西 西安 710049； 2 新能源系统工程与装备陕西省高校工程研究中心，陕西 西安710049； 3 动力工程多相流国家重点实验室，陕西 西安 710049）

引 言

气固流态化系统因其对颗粒相的连续处理能力、突出的传热传质性能以及宽广的操作范围[1]，被广泛应用于催化裂化[2-3]、煤气化[4-5]、固体废物及生物质热解[6-8]等能源化工过程中。在典型的气固流态化反应器中，受两相流动固有不稳定性的影响[9]，颗粒呈现出明显的时空多尺度分布特征[10]，形成尺度介于颗粒直径和宏观流动之间的介尺度结构[11]。这种介尺度非均匀结构将改变颗粒与气体间的相互作用机制，影响反应器内部的质量、动量和能量传递[12-14]，增加系统的非线性与复杂度，给反应器性能准确预测带来挑战。作为两相动量传递过程中最主要的作用[15]，气固相间曳力受到介尺度结构影响的同时也影响着介尺度结构的演化。认清二者间相互作用，并构建考虑介尺度结构影响的曳力模型，有助于提升反应器内部流动的预测能力，是进一步探索结构对质量和能量传递影响的基础，也是数值模拟技术在反应器设计、优化、放大及智能控制等方面推广应用的重要前提。近二十年来，诸多研究者在介尺度结构对曳力影响机理和考虑介尺度结构影响的曳力建模方法方面展开了探索，形成了两类主流模型：以能量最小原理多尺度（energyminimization multi-scale,EMMS）方法为代表的结构模型和基于介尺度结构完全解析模拟数据的过滤模型（filtered model）。本文对介尺度结构形成的影响机制和两类曳力模型构建流程与研究进展进行回顾和评述，曳力模型构建方面重点评述作者经验较为丰富的过滤模型，同时探讨未来过滤模型建模研究的发展方向。

1 介尺度结构的形成演化机制

在气固流态化系统中，随着进口流体速度增长，系统中的颗粒通常依次呈现出均匀膨胀、鼓泡、节涌、湍动、快速流态化及稀相输送多种流型状态[16]。除了Geldart A 类颗粒在气速介于最小流化速度与最小鼓泡速度之间时会呈现出均匀膨胀状态外，其他类型颗粒呈现出如鼓泡、团聚、条带等介尺度非均匀结构，这些结构从几倍颗粒直径到上千倍颗粒直径变化[10]，呈现出复杂的多尺度特征（图1）。为了清晰认识和理解介尺度结构特征的调控因素，方便进一步对其影响进行建模，很多学者对介尺度结构的形成演化机制从多个角度展开了研究。

1.1 控制方程稳定性分析

控制方程稳定性分析是研究初始状态伴有微小扰动的系统扰动发展（增大或衰减）的数学方法。自Anderson等[17]构建了描述气固两相流动系统的双流体模型以来，基于双流体方程的线性稳定性分析，成为了判别流态化介尺度非均匀结构发生的一种理论方法[18]。该方法判别式中各项的关系表明：由均匀流化系统开始到不稳定状态并产生非均匀结构的过程，受颗粒惯性和曳力随固含率变化关系共同影响[19]。气固相间存在速度差时，质量平衡扰动传播速度与动量平衡要求不匹配[20]，造成了颗粒局部富集。颗粒局部富集改变了曳力关系又进一步加剧了不稳定的发生，形成了颗粒富集与颗粒稀疏相间的一维结构[21]。虽然线性稳定性分析能够对均匀流化系统一次不稳定结构产生机制进行分析解释，但其无法预测后续结构是否向团聚或鼓泡进行演化。为解决这一问题，研究者还采用非线性分岔分析方法对垂直于流向的二次不稳定发生及演化的过程进行了研究[22-24]。研究给出一维结构准均匀状态和团聚鼓泡结构的区分方法，发现二次不稳定发生使颗粒富集区域下表面的颗粒如同下雨般降至下一层颗粒富集区域，这是形成团聚或鼓泡结构的主要机理（图2），当系统颗粒浓度高时形成鼓泡结构，反之则形成团聚结构[23]。稳定性分析的主要优势在于将扰动是否产生结构与尺度相关联，以找出不同尺度下产生结构的主要因素。比如针对均匀冷却系统（homogeneous cooling system，HCS）稳定性分析的研究中[25-26]，研究者依据产生不稳定的两个特征波数，将不稳定分为两种模式：一种是出现在小尺度的速度涡不稳定控制的剪切模式；另一种则是出现在更大尺度的团聚不稳定控制的热模式。这种多尺度的分析方法和非均匀结构时空跨度大的特征十分贴合。尽管稳定性分析具有上述优点，且已经描绘了重力、颗粒惯性、曳力和固相应力作用下介尺度结构的形成机制，但是其对结构形成过程的物理解释仍不是十分清晰。

1.2 固相压力局部平衡关系分析

团聚形成机制分析主要聚焦于粒化温度耗散过程，与气固流态化系统类似，颗粒流HCS 随着时间推移颗粒也会形成非均匀结构，这其中的影响主要源自颗粒碰撞产生的能量耗散。Goldhirsch等[27-29]对颗粒流均匀冷却系统中结构形成的机理进行了解释。具体而言，颗粒随机运动会产生局部颗粒浓度高的区域，局部颗粒浓度增强使颗粒碰撞频率增强，从而增强耗散使粒化温度及固相压力下降，周围高固相压力区域又会把颗粒推至这一区域，进而增强颗粒聚集。该过程的本质是随颗粒浓度上升而增大的固相压力关系在耗散主导的系统中发生了倒置（dps/dϕs<0，ps表示固相压力），颗粒聚集耗散的过程形成了正向反馈。当假设固相压力为局部固含率和粒化温度[θ(ϕs)]的函数时，固相压力对固含率的导数可以表示为

根据式（1），达成dps/dϕs<0 这一不稳定条件，取决于颗粒群抵抗压缩的能力（∂ps/∂ϕs）和粒化温度随固含率的变化关系（dθ/dϕs），后者则受到粒化温度产生与耗散的影响。利用这一关系，Fullmer 等[9]对气固两相流动中产生和抑制不稳定的因素进行了总结（图3）。颗粒间非弹性碰撞、颗粒间摩擦、由颗粒脉动速度产生的相间曳力都会在高固含率区域产生更强的粒化温度耗散作用，从而诱导结构产生，而颗粒平均流剪切、粒化温度热扩散（即粒化温度不同的区域通过颗粒运动及颗粒碰撞进行的脉动能量传递）和周围颗粒脉动通过局域流体对局部颗粒的影响则会减弱高低固含率间的粒化温度差异，起到抑制结构产生的作用。

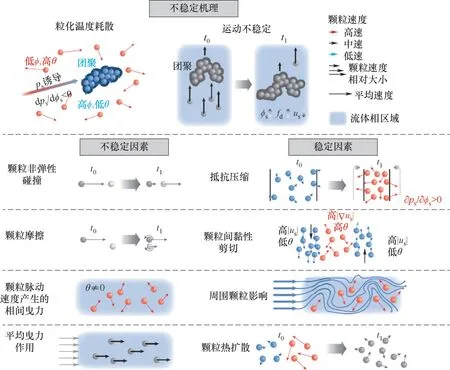
图3 固相压力平衡分析角度下的非均匀结构产生的影响机制[9]Fig.3 The mechanisms of generating inhomogeneous structures from the view of balance analysis of solid pressure[9]

1.3 低固含率系统中的其他因素

对于稠密气固流态化系统，由气固速度差引起的相间曳力和粒化温度耗散是介尺度结构形成过程中的重要影响因素，但随着固含率逐渐降低，颗粒接触产生的粒化温度耗散来源逐步减弱，且固含率与曳力的关系向线性转变，上述的两种诱导介尺度结构形成的因素的重要程度相应降低。此时载气的流动结构、颗粒运动的焦散效应、颗粒尾迹流动及壁面约束等其他因素或成为主导。在存在背景湍流的稀疏颗粒系统中，当颗粒直径较小、泰勒尺度Reynolds数较小、流动无复杂层级结构时，受离心作用影响，颗粒远离速度涡的中心向高剪切区域聚集，产生非均匀结构[30]。颗粒松弛时间尺度与湍动时间尺度越接近，这种聚集效应越明显[31-33]。这一机制在Stη<1（Stη为颗粒松弛时间与Kolmogorov 最小涡时间尺度之比）时能够很好解释非均匀结构的产生过程。当泰勒尺度Reynolds数增大到一定程度时，Stη>1，系统中将呈现出明显的层级结构特征，此时影响结构的不再是单一的流动特征尺度，在流动特征时间与颗粒松弛时间接近的尺度上，颗粒也会呈现出明显聚集结构[34-36]。为对这种情况进行预测解释，Goto 等[37]通过颗粒运动与流体加速度关联分析，提出了“清扫-粘连”（sweep-stick）机制。他们认为流体加速度场将以当地流体速度进行清扫，当颗粒跟随性较好时，颗粒经过流体加速度为0 的点会与之粘连共同运动，而在流体加速度不为0的位置，颗粒与流体间会因产生速度差而远离该点，最后形成颗粒倾向于在流体加速度为0 位置聚集的状态。由于沉降系统中重力和背景湍流的共同作用会影响结构特征[38]增强各向异性[39]，Falkinhoff 等[40]对“清扫-粘连”机制在颗粒沉降系统下进行了改进。Bragg 等[34]研究发现在Stη≫1 的系统中“清扫-粘连”机制将会失效，为此Oka 等[41]通过粗化到指定涡尺度的加速度场代替原先细网格加速度场，使颗粒松弛时间尺度能够扩展至流动积分时间尺度，即Stη≫1的系统。当颗粒松弛时间尺度继续增大，大于流动积分时间尺度时，颗粒运动不易受载气湍流影响，颗粒速度的空间分布函数的奇点主导了颗粒聚集结构，呈现出如泳池底部的光学焦散般的结构[42-46]，具体而言，初始单值分布的颗粒速度的空间分布函数，经历一定时间后，因速度快的颗粒追上了速度慢的颗粒，使分布曲线发生折叠，导致分布函数的空间导数发散（如图4中焦散效应所示）。发散一方面直接造成了颗粒聚集，另一方面因此处颗粒速度不同，颗粒间碰撞频率的增多进一步加剧了聚焦结构的形成[47]。而在颗粒Reynolds 数（Rep=ρguslipdp/μg）很大的系统中，流体经过颗粒后将产生长距离尾迹，其不但会对原本的湍流流场进行调制[48]，还会引入新的颗粒聚集机制，实验和数值研究[49-53]表明:在沉降过程中尾迹中的颗粒曳力将会明显降低，尾迹中的颗粒会追上产生尾迹的颗粒，从而促进颗粒聚集产生结构。Uhlmann 等[54]在无背景湍流的颗粒沉降系统中，找到了团聚现象产生的临界Galileo 数（重力与黏性力之比），并发现该临界值恰好与尾迹从轴对称变为涡旋交替的界限一致。更进一步，他们还在存在背景湍流的系统中，对背景湍流和尾迹对颗粒团聚的影响进行了研究[55]。另外，在存在壁面的管道或槽道流中，壁面约束为壁面附近的介尺度结构形成过程带来新的影响机制[56-59]，比如垂直于壁面方向上变化的流动特征尺度将改变局部Stη，使颗粒的富集程度沿垂直于壁面方向呈现变化分布特征；颗粒向湍流强度较低处聚集的湍泳（turbophoresis）现象在壁面附近更为明显，推动颗粒向壁面聚集。

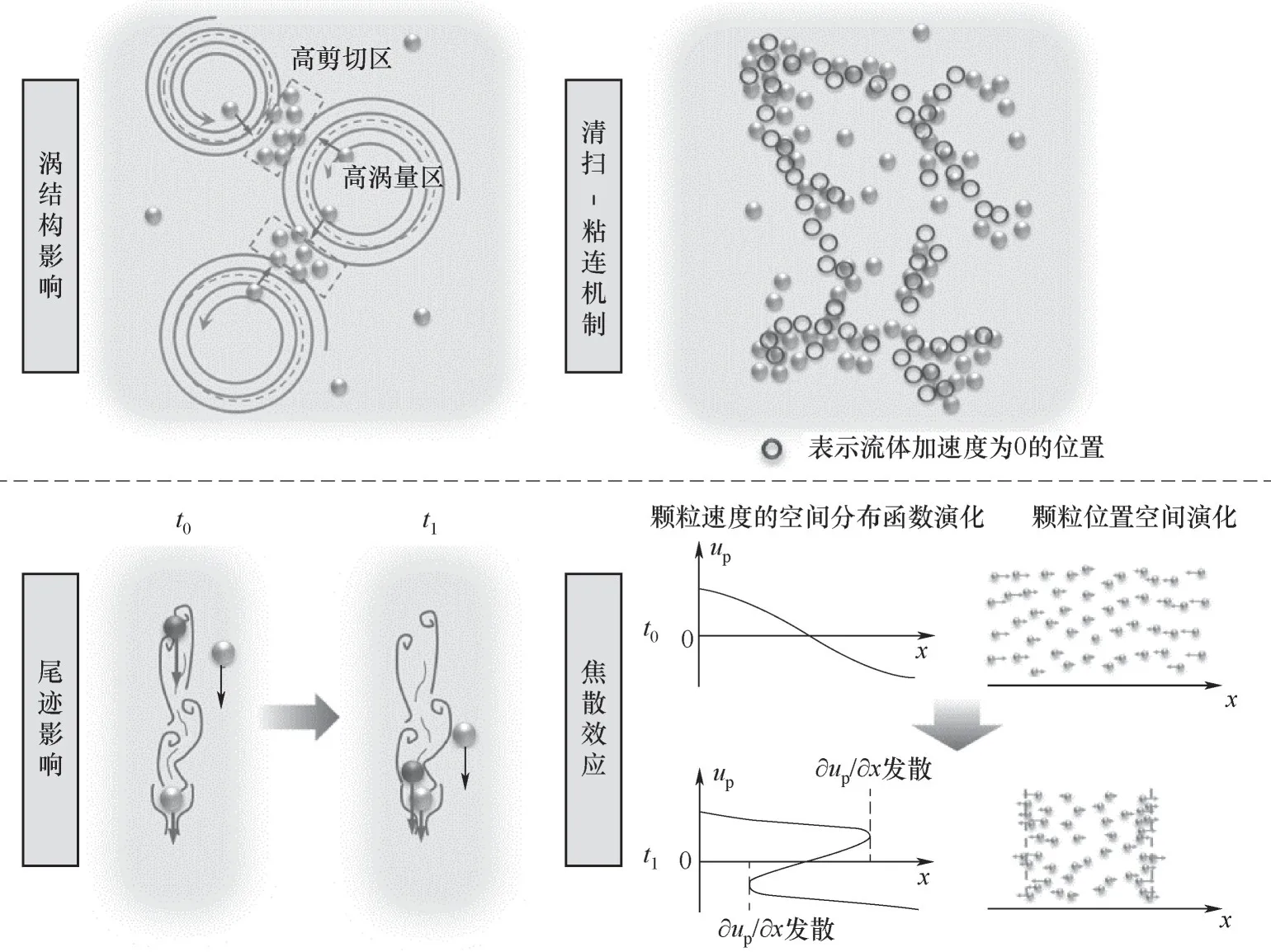
图4 低固含率条件下颗粒产生非均匀结构的影响机制Fig.4 The mechanisms of generating inhomogeneous structures for dilute gas-solid systems

1.4 统计热力学分析

上述机制多是遵循还原论的思路，从微观或局部视角出发，大多对单一因素主导的特征流动展开，难以直接解释流态化中多种机制耦合下的结构演化过程。为克服微观局部视角的局限性，一些研究者尝试从宏观统计特征出发，利用热力学分析手段，找出由均匀状态向非均匀状态转变的依据，将结构的形成和宏观统计特征的变化联系在一起。比如采用最小熵产率原理[60]对非均匀结构产生过程进行预测[61-62];在将颗粒产生非均匀结构类比为过饱和凝结过程的条件下，应用Gibbs 自由能变化分析团聚尺度[63]。这其中应用比较成功的是流态化研究发展而来的EMMS[64]原理，该原理认为微尺度下固相主导区域中颗粒倾向于重力势能最小，而流体主导区域流体倾向于流经路径中阻力最小，两种机制相互竞争协调，在宏观统计上表现为悬浮输送单位质量颗粒所消耗的能量最小。尽管这一稳定性条件有别于热力学中已有的极值原理，但其在数值模拟和实验过程中[65-66]的成功应用证明了它的合理性，这种合理性也驱动着很多研究者从热力学及统计角度进一步对其进行解释[67-69]。

气固流态化系统因其复杂多样的物理过程和派生出的丰富描述方法，促使研究者分别从流动控制方程的稳定性、固相压力局部平衡关系、低固含率下其他影响因素、统计热力学极值原理等多个角度展开了研究。这些研究揭示了气固平均速度差、颗粒脉动速度耗散、载气流动结构、颗粒运动焦散效应、颗粒尾迹效应等影响机制。尽管如此，气固流态化系统中介尺度结构形成演化的影响机制研究还有许多工作有待挖掘与完善，如壁面约束、颗粒黏性、球形度、多分散特征、反应过程产生的气体体积膨胀收缩效应对介尺度结构形成的影响以及多种机制的耦合作用。而如何深刻理解这些机制，分析不同机制下介尺度结构的特点，为理性考虑介尺度结构影响打下基础，则是更加值得探索的问题。

2 介尺度结构对曳力的影响机理

气固流态化系统演化出现非均匀结构后，系统的流动状态和相间动量传递特征将明显改变。从产生结构后的统计特征出发，颗粒浓度不再服从泊松分布，呈现出围绕浓稀两种固含率的双峰分布[70-73]。在这种分布特征下，受气流旁通作用影响，气相更倾向从团聚间隙或鼓泡这些稀相区域中绕行，当系统沿流向出现稀相通道时，大部分气流从稀相通道流过，系统气固滑移速度较均匀情况明显增大，而浓相颗粒感受到的气流速度大大降低，系统平均曳力也相应降低[13]，最大约降低一个量级[74]。极少数情况下（如柱塞流动），浓相将横向截住主流，气流会在浓相内部增速，使曳力较均匀系统有所升高[75-76]。本质上，局部颗粒实际的滑移速度与均匀系统的差异[13,15]引起了曳力的变化。根据上述分析，结构的特征与其对曳力的影响密切相关，鼓泡团聚结构的尺度特征、运动的统计特征及动态演化特征[77]都将影响气流通量浓稀相的分配，进而影响曳力。而结构的多尺度特征，还会使这种影响呈现出一定的尺度关联[78]，即介尺度结构对曳力的影响规律会随着观测尺度的不同而发生变化。

3 介尺度曳力模型的研究进展

在气固流态化的数值模拟中，当计算网格不足以对非均匀结构完全解析或计算网格内存在强梯度界面时，网格曳力将偏离均匀系统，继续使用接近均匀系统条件获得的曳力模型[79-82]将大大高估曳力[83-85]。因此，需要重新构建考虑未解析介尺度结构影响的曳力模型，本文将这种模型称为介尺度曳力模型。早期的研究者通过给均匀曳力乘以一个常系数[74]、用团聚直径代替均匀模型中的颗粒直径[86-87]、建立单颗粒与非均匀沉降阻力系数关系[88-89]、固含率分区选用不同经验关系[90-92]等方法，在实验数据基础上对曳力公式进行修正，以提升曳力预测的准确程度。其中，由Syamlal 等[88]提出的采用最小流化速度和最小流化速度对应的床体固含率对模型系数校准的方法，得到了较为广泛的认可[93-99]。在近二十年的研究发展中，介尺度曳力建模逐渐形成了两大主流研究范式（图5）。一类是从整体论角度出发，依据假定的非均匀结构，结合流体力学守恒关系、宏观参数与介尺度结构的实验关联关系和理论分析的稳定性条件，求解获得局部介尺度曳力本构关系（考虑介尺度结构影响的曳力与状态变量间的关联关系）。因其依赖于假定的非均匀结构，应用这种范式构建的模型称为结构模型。另一类则是从还原论角度出发，根据介尺度结构完全解析的模拟结果，应用过滤技术直接计算Reynolds平均或空间平均双流体控制方程中的曳力项，关联网格中状态变量（如固含率、滑移速度、过滤尺度等），构建介尺度曳力本构关系。一般称这种范式下构建的模型为过滤模型。

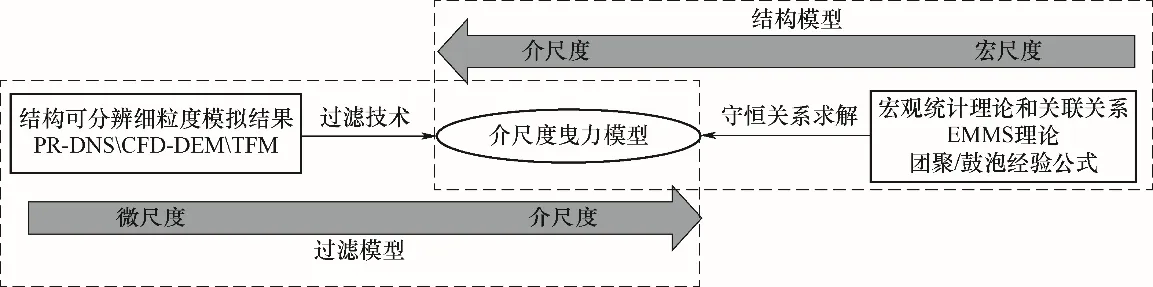
图5 介尺度曳力模型的两种建模类型Fig.5 The two categories of mesoscale drag modeling

3.1 结构模型

结构模型构建过程主要包含两个步骤：（1）找到符合实验或理论统计规律的主要结构特征（如浓稀相双峰分布、团聚或鼓泡大小、径向固含率分布等），依据这些特征将真实结构向易于建模的方向进行假定与简化；（2）对简化结构建立动力学描述方法，关联宏观操作参数和结构状态特征，结合守恒关系、实验关联关系或稳定性条件构建曳力模型。其中预测性能优秀并得到广泛应用的是EMMS曳力模型。典型的EMMS 曳力模型[100-102]根据局部固含率双峰分布统计特征[70-73]，将颗粒非均匀结构假定为一定比例的浓相团聚和稀相背景。在这样的结构下，系统由两相变成了四相（浓相气体、浓相颗粒、稀相气体、稀相颗粒），原本非均匀系统的相间动量传递则被多尺度地解析为稀相相间、浓相相间、稀相气相与浓相团聚间三个均匀子系统的相间动量传递。这样仅求解出这三个子系统的状态参数，即可获得系统相间曳力大小。通常平衡关系中状态变量数要比守恒关系构建的方程多，通过添加EMMS 稳定性条件和一些实验关联关系（如颗粒团聚大小关联式、浓稀相颗粒加速度相等、团聚内部固含率关联式等），实现方程封闭，求解获得系统曳力。在近十年的发展中，与EMMS 曳力模型类似的结构模型在多方面进行了发展延伸，诸如改进实验关联关系[103-106]、调整稳定性条件[101,107]、基于鼓泡结构建模[108-109]、扩展到多分散系统[110-112]以及考虑颗粒脉动及结构演化特征[107,113]的影响等。关于EMMS曳力模型更为系统的评述见文献[14,114-117]。

在气固流态化系统中，结构模型一般通过模拟结果与实验结果相互比对的方式，对构建的曳力模型性能进行评价。常选用实验方便测得且在工程应用具有重要意义的参数进行比对，如固含率轴向分布、固含率和气固速度径向分布、颗粒循环通量、颗粒停留时间、鼓泡床高、鼓泡直径的统计分布等[106,118]。另外，与已发表的模型比对曳力随固含率的变化情况也是一种简单检验的方式[119]。

结构模型的建模方式具有很明显的工程应用特征，能够直接利用统计热力学稳定性分析原理和实验中宏观参数与介尺度结构的经验关系，针对流态化系统中实际存在的结构现象构建模型，在不同物性及宏观操作参数的系统中实现了广泛实验验证，在实验室乃至大型工业尺度获得了较好的预测性能[116,120]。

3.2 过滤模型

与结构模型使用宏观统计获得的理论和经验关系不同，过滤模型则是从介尺度结构完全解析的模拟数据出发，自下而上地对介尺度曳力进行建模。类比于单相湍流中速度脉动未解析情况的建模方法，研究者采用Reynolds/空间平均过滤技术，对原始的气固两相流控制方程进行推导，获得网格内部存在非均匀结构情况下依然适用的气固两相流控制方程[84,121-122]。根据方程中基于结构完全解析模拟数据的显式表达式，可采用过滤技术直接获得介尺度曳力，通过分类条件平均的方法研究网格内状态变量与曳力的关联关系，进而构建介尺度曳力模型（图6）。

图6 过滤模型构建流程示意图Fig.6 The modeling process of filtered model

（1）细粒度数据生成 本文中，将介尺度结构完全解析的模拟称为细粒度（fine-grained）模拟，而细粒度模拟产生的数据则称为细粒度数据。与细粒度模拟对应的是介尺度结构并未被网格完全解析的粗粒度(coarse-grained)模拟，粗粒度模拟将未解析的介尺度结构影响以平均化模型的形式考虑到控制方程中，介尺度曳力建模所服务的模拟方法就是一种粗粒度模拟方法。显然，细粒度模拟数据是上述过滤模型建模过程的基础。细网格双流体模型（TFM）[84-85,123]、CFD-DEM[124-126]和颗粒解析的直接数值模拟（PR-DNS）[78,127]由于介尺度结构完全解析，均可作为细粒度数据生成的模拟方法，其中细网格TFM 和CFD-DEM 模拟中曳力采用均匀曳力模型进行封闭（如基于实验的Wen-Yu 模型和基于PR-DNS 模拟的BVK 模型）。当然采用PR-DNS 数据能够最大程度上保证建模的可靠性，采用CFDDEM 数据也能够很好地确保颗粒间碰撞受力的准确性，但较大的计算机资源消耗限制了两种方法模拟区域的大小，进而限制模型构建的尺度。得益于较低的计算资源需求和良好的宏观参数预测能力[128-129]，尽管细网格TFM 应用于气固系统的前提假设还存在争议[28-29,130]，且基础模型的选择对模拟结果会产生一定影响[131-132]，但并不妨碍[130-131]其成为目前介尺度曳力建模中最常用细粒度模拟方法。除了用于产生数据的模拟方法，研究中产生数据的物理系统也各不相同，如压力驱动的周期气固系统[84]、微型流化床系统[123]和周期提升管系统[85]。在后两种体系中壁面带来了剪切的影响，从早些年Agrawal等[83]对剪切边界条件气固周期系统研究可知，宏观剪切会影响系统中非均匀结构的表现形式；增强剪切率会让系统更易形成细长条状的非均匀结构。因此，这两种系统在产生数据时，壁面边界条件设置、系统的几何尺寸都会对数据的分布特征造成影响。从理性建模的角度看，先构建周期系统下的模型，再使用依据壁面影响进行修正，更加合理。选择二维或三维的模拟系统也是值得讨论的问题，受计算能力制约，三维周期系统很难在达到尺度无关的计算域上开展计算[133-134]，而二维系统虽然能够定性展示结构演化规律，但维度的约束还是使得产生的结构与真实三维系统存在一定差异[134]。

在构建模型的评价方法上，过滤模型比结构模型有着更加多元的评价手段。过滤模型本身源自细粒度数据，与细粒度数据是否吻合成为检验模型的天然标准。比较过程中，将不求解控制方程直接应用细粒度数据代入模型进行检验的方法称为先验分析（priori analysis）。先验分析中常使用模型预测值与细粒度数据值间的Pearson相关系数、决定系数、均方误差、平均绝对百分误差和相对误差的概率密度分布函数等指标来评价构建模型的预测能力[145-147,150]。先验分析能对构建的模型进行初步判断，对数据关联过程和状态变量的有效程度进行检验。将模型嵌入到求解体系中进行模型检验分析的方法称作后验（posteriori test），后验中常通过比较相同系统下粗粒度和细粒度模拟结果对模型进行评价。后验更加充分地反映了模型实际应用时的预测效果，但同时也引入了建模外的其他影响因素，比如状态变量使用梯度量时引入了离散误差、求解过程中方程离散误差与模型的耦合作用、方程中其他模型选择带来的不确定性影响。由于细粒度模拟比实验数据更加丰富，因此后验中可比较的物理量也更加多样。过滤模型的后验也可以类似结构模型使用实验数据作为标准开展。

经过二十多年的发展，过滤模型在上述建模各个环节上都积累了丰富的经验，尤其变量和关联关系建立方面，经历了由直接建模到借助脉动关联变量、由基本状态变量到多种状态变量、由函数模型封闭到输运方程封闭、由数据分析拟合到机器学习建模的转变过程。尽管建模方法日趋成熟，但模型的预测效果和通用性方面仍存在较大的改进空间。为深入了解模型特性，进一步提升模型预测性能，还应从更理性的角度对物理层面的问题探讨研究。

（4）考虑曳力各向异性特征 依据重力方向曳力与其他方向曳力的量级差异，很多研究仅采用重力方向曳力数据进行建模研究，并假设曳力具有各向同性特征，将重力方向获得的曳力系数或非均匀因子直接用于其他方向。但是，过滤曳力与过滤滑移速度方向并不总是完全一致，这一现象[15,85,134]从侧面反映了曳力系数实际上存在各向异性的特征。针对这一问题，Milioli 等[135]根据二维周期模拟结果指出：重力方向与非重力方向的曳力系数确实存在差异，但差异相对较小，采用各向同性假设构建过滤曳力模型仍具有一定合理性。但是Cloete 等[131,134]依据二维模拟数据分别构建了各向异性与各向同性曳力模型，并采用先验与后验结果对两种模型进行了对比，结果表明，尽管非重力方向曳力与重力方向曳力相比相对较小，但非重力方向曳力的影响并不能忽略，考虑曳力系数的各向异性才能获得与细网格模拟较为接近的结果。实际上，之前提到的近似反卷积[153-154]和卷积神经网络[147]，方法自身性质就赋予了其考虑结构各向异性特征的能力，在原有体系下稍作扩展便可实现曳力的各向异性。尽管输运方程方法[122,140-141]需要依据数据确定方程封闭的模型系数，但模型框架基本确定，涉及参数相对较少，向各向异性扩展相对容易。而函数型建模方法，由于重力方向和非重力方向主导机制可能不同，还需要重新寻找合适的状态变量构建关联关系。

（5）宏观影响并未引入 大多数建模研究将不同总体固含率下流态化或沉降系统的模拟数据汇总在一起，用过滤尺度内平均获得的局部状态变量进行关联建模，并不考虑宏观状态参数的影响。这种做法的前提是过滤曳力与宏观状态参数无关，即宏尺度与介尺度存在尺度分离，目前研究表明流态化系统中这种尺度分离并不存在[155-157]。另外，Mouallem 等[158-160]的研究表明宏尺度的状态参数对本构关系的构建影响明显。因此，将宏观状态参数考虑到建模过程中十分必要。宏观参数并不会直接作用于网格内未解析结构的演化过程，而是通过已解析流动由反应器尺度逐级地向网格尺度进行传递，因此局部网格周围的信息间接承载了宏观参数的影响，采用局部网格周围的信息进行建模，能够为宏尺度与介尺度建立联系。最近，Jiang 等[136]从这一思路出发，将以局部网格为中心的三倍网格尺度区域的固含率作为一个新的状态变量加入到建模过程中，提升了模型对流型的适用能力。实际上，动态调整技术[85]、近似反卷积[153-154]和卷积神经网络[147]的建模方式，因其构建过程本身就依赖于周围信息，天然地将宏观影响也考虑到了模型当中。

（6）壁面效应与剪切流动影响 前面提到的寻找与过滤曳力相关联物理量的研究中，建模数据大都源自Geldart A 类颗粒物性条件下的单分散周期系统。而实际应用环境中，存在壁面是真实流态化系统与周期系统最明显的差别，许多研究者[85,123,126,145,161]采用包含壁面的真实流态化系统进行了过滤曳力建模工作。其中Igci等[161]重点分析了不同固含率下，壁面剪切效应对过滤曳力系数的影响，采用壁面距离相关的衰减函数对过滤曳力进行修正，后验得到了与细网格结果相近的宏观统计特征。壁面的剪切作用主要通过改变结构取向与厚度影响过滤曳力[83]，其影响范围和强度会随颗粒性质、颗粒与壁面滑移程度、流动的剪切强度发生变化。例如，剪切强度较低时，固相应力应变关系趋于牛顿流体，随着剪切强度增加，颗粒会呈现出一定取向层状结构，非牛顿流体的效应也随之增强[83,162]，壁面附近结构会发生本质的变化，仅采用特征长度无量纲的壁面距离很难全面反映这些变化的影响。在稠密气固系统中，类似单相湍流中描述边界层变化规律的无量纲壁面距离，仍有待去发现与总结。

（7）物性的影响 由于细粒度模拟数据积累不易，很多建模工作在指定物性的系统下展开，当这些模型应用于其他物性的系统时，往往预测效果并不理想[136,146,148,163]。为解决该问题，Zhu 等[164]以过滤固含率、过滤滑移速度和诸多物性参数为建模参数，在周期沉降系统中，利用压力的平衡关系构建了过滤曳力模型，并在大量不同物性的快速流化床系统中进行了模拟验证，与实验对比的结果表明：模型在一定网格尺度上显示出了良好的预测能力[165]。Jiang 等[148]通过在模型中引入基于颗粒终端沉降速度的颗粒Reynolds数的方法来考虑物性的影响，与细网格TFM 结果对比发现：模型在不同物性的鼓泡床系统中也取得了令人满意的结果。但是，最近Jiang 等[136]将Jiang 等[148,164]提出的物性修正关系应用于不同流型的系统时，在流型与建模流型差异较大的情况下，修正关系模型模拟结果与相应系统下直接构建模型的模拟结果仍存在一定偏差，似乎在不同流型下，物性对过滤曳力的影响也有所区别。相比于函数型模型，采用输运方程方法在方程封闭建模中涉及的模型系数相对较少，对物性的敏感性可能相对较低[141]。从结构的形成机制上看，物性不同，将改变结构产生和维持过程中多种影响机制间的关系，主导机制的变化将改变非均匀结构在不同尺度上的分布特征[166]。因此，从物性对结构的影响机制出发构建模型，也许是未来解决这一问题的关键。

（8）过滤尺度关联问题 在很多建模工作中，过滤尺度常被当做一个关键的状态变量加入到模型的关联关系中，但是在实际粗网格计算时，如何确定过滤尺度是一个值得讨论的问题。一些研究[123,145,148]直接认为过滤尺度和应用的粗网格尺度相等，但另一些研究[150,163]则根据湍流LES 中的经验认为过滤尺度是应用网格尺度的两倍。Gao 等[167]通过在1～3倍的范围内调整过滤尺度和实际应用粗网格尺度之比，比较了构建模型在不同流型系统中的后验效果，发现在Wei 等[168]的实验循环流化床模拟中，过滤尺度与粗网格尺度之比对结果影响明显，且通过与实验结果对比，给出了与实验吻合较好的最优比值。Cloete 等[142]通过和细网格结果对比，在其研究工作中也得到了类似结论，并且他们还发现这个最优比值会随着模型表达式及选用状态变量的不同而发生变化。这种针对特定粗网格模型和模拟系统寻找最优过滤尺度与粗网格尺度比的过程，大大降低了过滤模型的通用性。为解决这一问题，可以将最优比值和模拟系统的关联预先也构建在模型当中，或者直接构建一个与过滤尺度无关的曳力模型。在最近的研究中，Zhu 等[151]发现将压力梯度作为状态变量加入到建模过程中时，曳力达到了近似尺度无关的效果。而Jiang 等[136]在压力梯度基础上又加入了更大尺度固含率作为状态变量进行建模，模型表现出更加明显的尺度无关特征。尽管已有工作得到了与过滤尺度无关的模型，但其实际效果还需要进一步的验证。

除了上述关键问题，近十多年，研究者还在双分散系统各分散相过滤曳力建模[126,169]、内部埋有阵列管线的流态化系统过滤曳力建模[170]、欧拉-拉格朗日框架下粗粒化颗粒过滤曳力建模[124-126]、黏性颗粒系统与非黏性颗粒系统中脉动关联矩与曳力关系比较[143]等方面对过滤模型进行了拓展。综上，过滤模型因其依赖于细粒度高分辨率模拟数据，模型构建从底层演化结构出发，构建模型所依据的非均匀结构比较真实。模型构建过程倾向于从脉动关联矩统计分析和动力学角度分析结构的影响，所应用的过滤技术与湍流LES 建模相似，LES 中很多实用的理论及建模思想可以迁移应用到过滤曳力的建模中来。但由于选定的模拟系统与方法决定了状态参数和曳力数据的分布特征，构建模型的适用范围会受到模拟数据特征的限制。积累覆盖更广的参数范围的模拟数据，更紧密地结合结构产生机制，在模型中加入更具物理意义的表征参数以及构建物性和流型适用性更强的模型是未来过滤模型研究的重要努力方向。

4 介尺度曳力模型的工业应用

近些年，在计算流体力学和多相流理论快速发展的背景下，计算流体力学辅助设计可以很大程度上节约设计成本并降低实验风险。其中介尺度曳力模型也扮演着十分重要的角色，得到了一定应用。如在中科院过程工程研究所与中石化石油化工科学研究院合作的多产异构烷烃的催化裂化工艺技术（maximizing iso-paraffins，MIP）研究中，基于EMMS模型的CFD模拟被用于流动结构和几何参数影响的分析，指导了安全操作参数空间的工况寻优工作，并在后续MIP 放大过程发挥了关键作用[171-173]。在中科院过程工程研究所与大连化学物理研究所关于甲醇制烯烃技术（methanol to olefins，MTO）研究的合作中，基于EMMS 曳力模型的CFD模拟还应用在了MTO 反应器放大过程，分别对微尺度、中试尺度、示范尺度、商用尺度反应器进行了模拟，分析几何结构放大对流动结构和反应产物分布的影响规律[174-177]。另外，还有一些研究将结构模型应用在循环流化床煤气化反应器[178-179]、中试循环流化床碳酸化反应器[180]、循环流化床锅炉[181]、烯烃聚合反应器[182]、生物质气化[183-184]等装置的模拟中。相比于结构模型，过滤模型的工业应用并没有那么广泛，大多集中在实验室和中试尺度。如Yu等[185]采用Gao 等[163]构建的模型，对催化裂化的中试循环流化床进行了冷态模拟，得到了和实验相近的颗粒停留时间的分布特征；Yu 等[186]将Ozel 等[85]开发的模型应用于较大尺度流化床反应器实验装置，模型展现了很好的网格无关特征，预测的密度轴向分布曲线与实验吻合良好；Schneiderbauer等[187]将其构建的过滤模型应用于熔融还原炼铁的流化床系统，在固含率和还原过程预测方面，模拟得到了与实验接近的结果。尽管过滤模型已经在特定的工业系统中得到了应用，但要如结构模型一般，实现在不同层次、不同颗粒物性、不同流型、不同种类的设备中广泛应用，过滤模型的通用性和普适化能力还有待进一步提升。

5 结语与展望

为满足工业生产对气固流态化技术发展的新需求，提升介尺度结构影响下流动过程的预测能力，研究者对结构形成的影响机制和结构对曳力的影响进行了大量研究。在结构形成的影响机制方面，相关研究工作从气固两相流动的控制方程的稳定性分析、固相压力局部平衡关系、低固含率系统中的其他因素、统计热力学分析多个角度进行了挖掘，总结了气固平均速度差、颗粒脉动能量耗散、载气流动结构、颗粒运动焦散效应、颗粒尾迹效应等影响机制。在结构对曳力的影响方面，相关研究工作揭示了介尺度结构对曳力的影响机理，并构建了考虑介尺度影响的曳力模型，其中基于假定结构求解分析的结构模型和基于细粒度数据过滤的过滤模型得到了广泛的应用与发展。相比于更为成熟的结构模型，过滤模型还处于提升模型普适性的阶段。在经历了从网格状态量直接建模向以脉动关联矩为桥梁借鉴湍流LES中建模方法的思路转变之后，过滤模型的研究从建模技术又回归到了物理本质，在更为理性寻找新状态变量、考虑曳力各向异性特征、考虑宏观状态参数影响、引入壁面效应、增强模型对不同物性适应能力等方面进行了一定探索。

服务工业流态化过程模拟是介尺度曳力建模研究目的之一，模型在工业设备设计、优化、放大过程中的应用情况是检验模型效能的最终指标。在这一点上，结构模型已在多个领域的工业设备展现出了令人满意的成绩，而过滤模型受其所处发展阶段影响，通用性和准确性仍有待完善。为进一步提升过滤模型的预测能力，未来还可在以下几个方面开展进一步工作。

（1）根据结构模型中EMMS 理论在不同系统中应用的成功经验，从结构形成演化机制中提炼的条件和关系，往往具有更强的普适性。立足于这一点，过滤模型的建模工作应更加深入挖掘并结合结构形成演化机制，加入更具物理意义的参数进行理性建模，以增强模型在不同系统中的适应能力，提升通用性。

（2）介尺度结构形成演化过程呈现出时空多尺度结构特征，并受多种机制调控影响，不同物性和流型将改变演化过程中的主导机制，使各个参数变量与曳力之间的函数关系变得极为复杂。现今，机器学习与人工智能技术已为处理这类问题提供了便捷的解决方案，其对复杂问题的处理能力与流态化中时空多尺度、多种机制影响的性质相适应。此类技术在过滤曳力建模中进一步应用值得期待。

（3）实际系统中，多分散、颗粒非球形、颗粒黏性及反应过程产生的气体体积膨胀收缩等特征都会对介尺度非均匀结构形成和演化产生影响，进而改变相间曳力规律。因此，探明以上特征对过滤模型影响规律，构建适用于真实系统模型值得进一步研究与探索。

符 号 说 明

Fd——考虑压力梯度脉动与固含率脉动关联矩的过滤曳力，N/m3

fd——曳力，N/m3

kg——气相拟湍动能，m2/s2

ks——固相湍动能，m2/s2

pg——气相压强，Pa

ps——固相压强，Pa

Rep——以颗粒直径和滑移速度为特征长度和速度的颗粒Reynolds数

r——积分变量，表示积分域V中一个空间位置

Stη——以Kolmogorov 最小涡时间尺度作为流动时间尺度的Stokes数

t——时间，s

t0——初始时刻，s

t1——经历一定演化时间后的时刻，s

ud,g——气相漂移速度，m/s

ud,s——固相漂移速度，m/s

ug——气相速度，m/s

up——颗粒速度，m/s

us——固相速度，m/s

uslip——滑移速度，m/s

x——水平位置坐标，m

x——空间坐标，m

βh——颗粒分布均匀条件下相间动量交换系数，

N·s/m2

Δf——过滤尺度，m

θ——粒化温度，m2/s2

μg——气体动力黏度，Pa·s

ρg——气体密度，kg/m3

ϕg——气含率

ϕs——固含率

上角标

′——脉动量

——空间过滤

～——相加权空间过滤

下角标

g——气相

s——固相

slip——滑移

0——初始时刻

1——经历一定时间某时刻