基于介尺度稳定性条件的多相流曳力与群体平衡模型

管小平，杨宁

（中国科学院过程工程研究所，多相复杂系统国家重点实验室，北京 100190）

引 言

多相流广泛存在于化工的单元操作，比如输送、精馏、结晶、干燥、反应等，是传递-反应的重要媒介。化工多相流呈现非线性、多尺度、多流型的特征，直接影响着传质、传热和反应速率，是工艺过程放大困难的根源。比如，对于气固两相流，随着操作条件的变化，出现固定床、鼓泡床、湍动床、快速床以及输送床流型，床内涉及小尺度单颗粒、介尺度气泡或者颗粒团、大尺度全床的流动行为。因此，复杂多尺度结构的解析及形成机理是科学认识化工多相流的难点。

近些年，计算流体力学(computational fluid dynamics,CFD)成为认识多相流的重要手段，包括直接数值模拟(DNS)、欧拉-拉格朗日方法以及欧拉-欧拉方法[1]。欧拉-欧拉方法的模型是对单相流模型采用平均化方法得到的连续介质多流体模型[2]。模型中含有额外的非封闭项，用于描述相内或者相间微观相互作用对宏观流动的影响。常见的封闭子模型包括相间作用力模型、聚并破碎核函数以及湍流模型。相间作用力模型用于封闭由于相界面上黏性应力和压力分布不均产生的平均作用力，包括曳力、升力、虚拟质量力、湍流扩散力以及壁面润滑力等[3]。聚并破碎核函数针对的是分散相内部的相互作用，描述分散相聚并破碎过程的动力学，包括聚并速率模型、破碎速率模型以及子气泡分布模型[4,5]。湍流模型用于封闭速度脉动产生的额外应力，包括大涡模拟和雷诺平均湍流模型。尽管多流体模型框架经过严格的数学推导，解决了宏观输运尺度的动量传递问题，但将多相流的物理复杂性转嫁到封闭子模型中，关键科学问题并没有解决。

从介科学角度发展介尺度物理模型，解析多相流非均匀结构演化的控制机制，是认识多相流复杂性的新途径。介尺度模型提出于20 世纪80 年代末，针对气固流态化体系，认为在物理上流态化系统存在稀、密相两种不同的运动机制。两种机制的竞争协调构成了系统的介尺度稳定性条件，是系统介尺度结构形成及演化的推动力[6]。21 世纪初，该方法拓展至气液鼓泡体系，认为体系存在有利于形成大气泡和小气泡的两种形态机制，两种机制的竞争协调决定了气泡形态的演化[7]。进一步将介尺度模型与CFD 相结合，为发展多相流模型提供了新思路。

通过介尺度理论模型，导出两类介尺度封闭模型：介尺度曳力模型和介尺度群体平衡模型，本质上是通过介尺度稳定性条件决定系统的介尺度结构和封闭模型。将该封闭模型与多流体模型耦合，可用于多相流装备的模拟计算，实现了介尺度模型从理论到实用的跨越。本文将从能量最小多尺度方法、介尺度曳力模型、介尺度群体平衡模型以及模型应用四个方面进行综述，讨论模型的发展历程以及模型在实际体系的应用，最后对该方向的发展进行展望。

1 能量最小多尺度方法

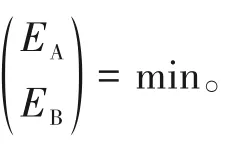
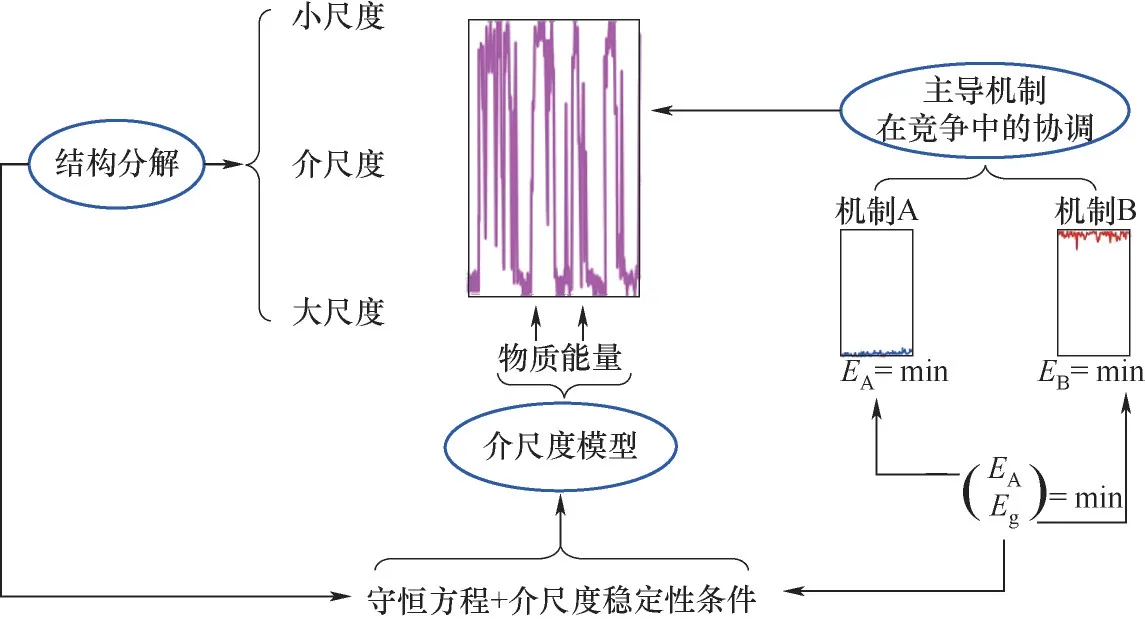
图1 EMMS方法的总体思路[9]Fig.1 General framework of EMMS approach[9]

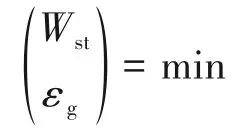
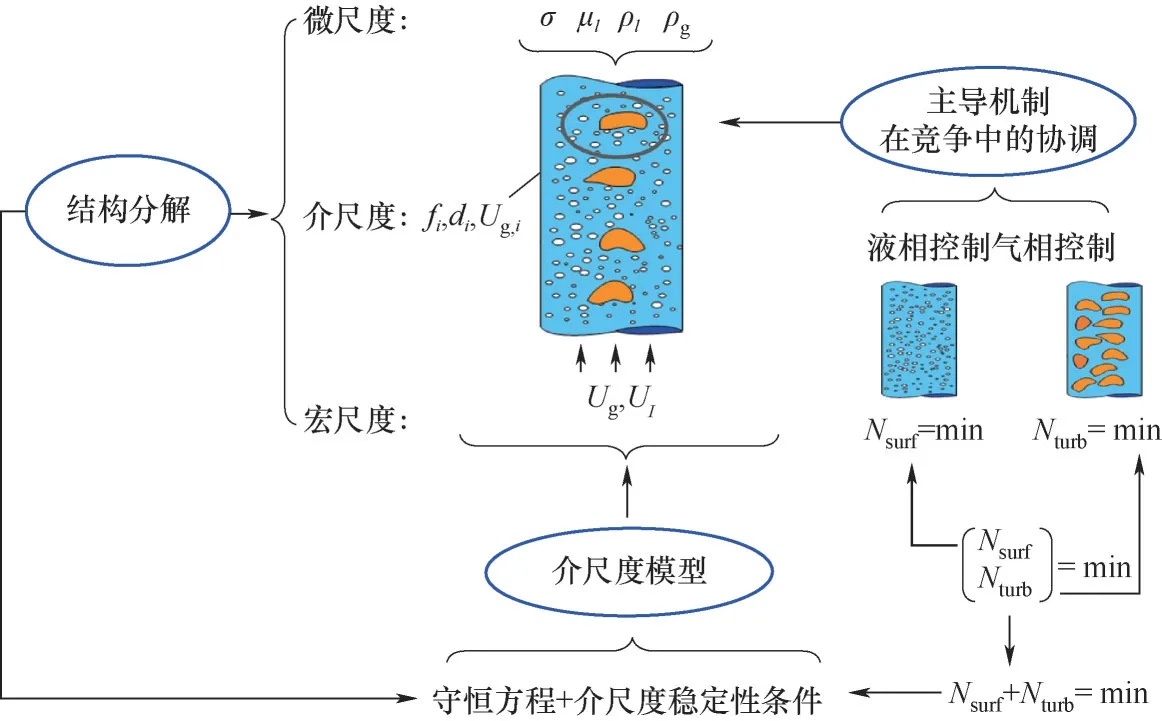
图2 气液体系的介尺度理论模型[7]Fig.2 A mesoscale model for gas-liquid bubbly flow[7]

介尺度理论模型结果表明[12-14]，对于空气-水体系鼓泡塔，随着表观气速增加，气含率增大，但在表观气速0.101 m/s 时，气含率发生跳跃，由0.275 降低至0.248，出现动力学系统中的“分岔”现象，反映了系统本征稳定性的变化规律，流域由此过渡到湍流鼓泡区。数学上，在过渡点附近Nst存在两个极小值，而Nst=min 在两个极小值间发生了转化，导致了系统结构参数的跳跃，物理上表现为系统在两个稳定状态之间发生转变，宏观流域发生了过渡。可见，理论模型能很好地阐明宏观流域过渡的介尺度物理机制[7,12,15]。

Ruzicka 等[16-17]的实验表明，黏度或者表面张力对气液流动稳定性呈双重影响：在低黏度或者表面张力时，增加黏度或者表面张力有利于流动稳定，流域过渡延迟；而在高黏度或者表面张力时恰恰相反。Yang 等[12]发现介尺度理论模型预测的跳跃点能反映此双重效应：当黏度由1.0 mPa·s 增加至3.0 mPa·s 或者表面张力由20 mN/m 增加至40 mN/m 时气含率跳跃点向高表观气速移动，流域过渡延迟；进一步增加黏度或者表面张力，跳跃点向低表观气速移动，流域过渡提前。

需要指出的是，基于EMMS 方法的介尺度理论模型是零维概念模型，反映的是体系多相流的内在本征稳定性，并不包含装置结构(如塔径、气体分布器以及内构件等)外在因素的影响。对于有外在因素影响的实际问题，需要求解完整的介尺度稳定性条件约束的多流体模型(stability-constrained multifluid model, SCMF)。但是，该完整模型的求解需要在每个时间步内进行优化计算，在技术上和计算量上目前都还比较困难。可以采取一种简化的稳定性条件约束的多流体模型，如图3 所示。对于计算单元建立介尺度稳定性条件约束的稳态守恒方程，获得单元结构信息参数，然后重构介尺度曳力模型或者介尺度群体平衡模型，再耦合到平均化的多流体模型控制方程中去。该方法通过介尺度本构模型这一桥梁间接实现了稳定性条件对多流体模型的约束。下面将详细介绍介尺度曳力和介尺度群体平衡模型及模型的应用。

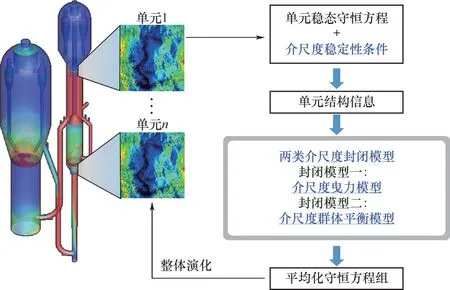
图3 简化的稳定性条件约束的多流体模型Fig.3 Simplified multi-fluid model constrained by stability condition

2 介尺度曳力模型

曳力是多相流中连续相和离散相之间重要的相间作用力，分散相受到的单位体积平均曳力大小为：

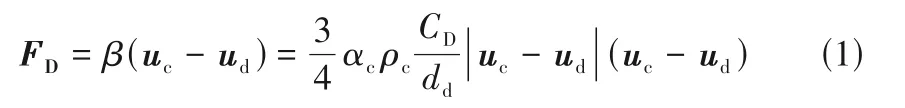
其中，β为平均相间曳力系数；uc为连续相速度；ud为分散相速度；αc为连续相含率；ρc为连续相密度；CD为有效曳力系数；dd为分散相粒径。Yang 等[18]首次从介尺度理论模型的结构参数重构了考虑颗粒团聚物影响的气固曳力模型，并用于循环流化床的CFD 模拟。模拟结果表明，与Wen&Yu/Ergun 曳力模型相比，该介尺度曳力模型能很好地捕捉颗粒聚团现象，床层颗粒夹带量与实验值更加符合，还可以预测快速流态化的噎塞现象。Wang 等[19]采用两步法建立了曳力系数与计算网格内相含率及气固速度的关系，模型能捕捉S 型轴向固含率分布。近些年气固流态化体系的介尺度曳力模型在介尺度结构参数模型化[20-21]、拓宽应用流域范围[22]、与人工智能结合[23-24]以及实际应用[25-26]等方面取得重要进展，大幅推进了该研究领域的发展及影响力。

在气液体系，有效曳力系数和气泡粒径都是体系的未知参数，随着操作参数而改变。但是，如式(1)所示，有效曳力系数CD和气泡粒径db比值的大小决定了多流体模型中的平均相间曳力系数β。因此，从介尺度理论模型结构参数重构这一比值足以实现与多流体模型的耦合，并不需要具体指定曳力系数的修正因子或者气泡粒径的大小。Chen 等[27]、Yang等[13]以及Xiao等[14]计算了不同表观气速下鼓泡塔的CD/db的大小，并建立了CD/db和表观气速Ug之间的数学关联式，如表1所示。

Yang等[13]以及Xiao等[14]将该介尺度曳力模型应用到鼓泡塔的CFD 模拟。如图4 所示,将介尺度曳力模型和CFD 模型耦合后，总体气含率随表观气速增加而增大，但进入湍动流域后总体气含率随表观气速变化不显著，出现平台现象。传统曳力模型只能预测气含率单调递增，而介尺度曳力模型与实验结果更加相符。仅用基于EMMS的介尺度理论模型总体气含率有跳跃现象，表明流型发生了过渡。但理论模型是零维概念模型，仅能反映体系内在的本征稳定性，不能考虑设备结构外在因素的影响。将理论模型导出的介尺度曳力模型与CFD 结合后，可以考虑外在因素的影响，提高了总体气含率的预测。Xiao 等[32]还考察了将鼓泡塔系统分成气相及水相的两相模型、稀相(大气泡)及密相(小气泡和水)的两相模型和大气泡相、小气泡相及水相的三相模型，分别结合相应的介尺度曳力模型，均能很好地预测总体气含率、气含率及液速径向分布。

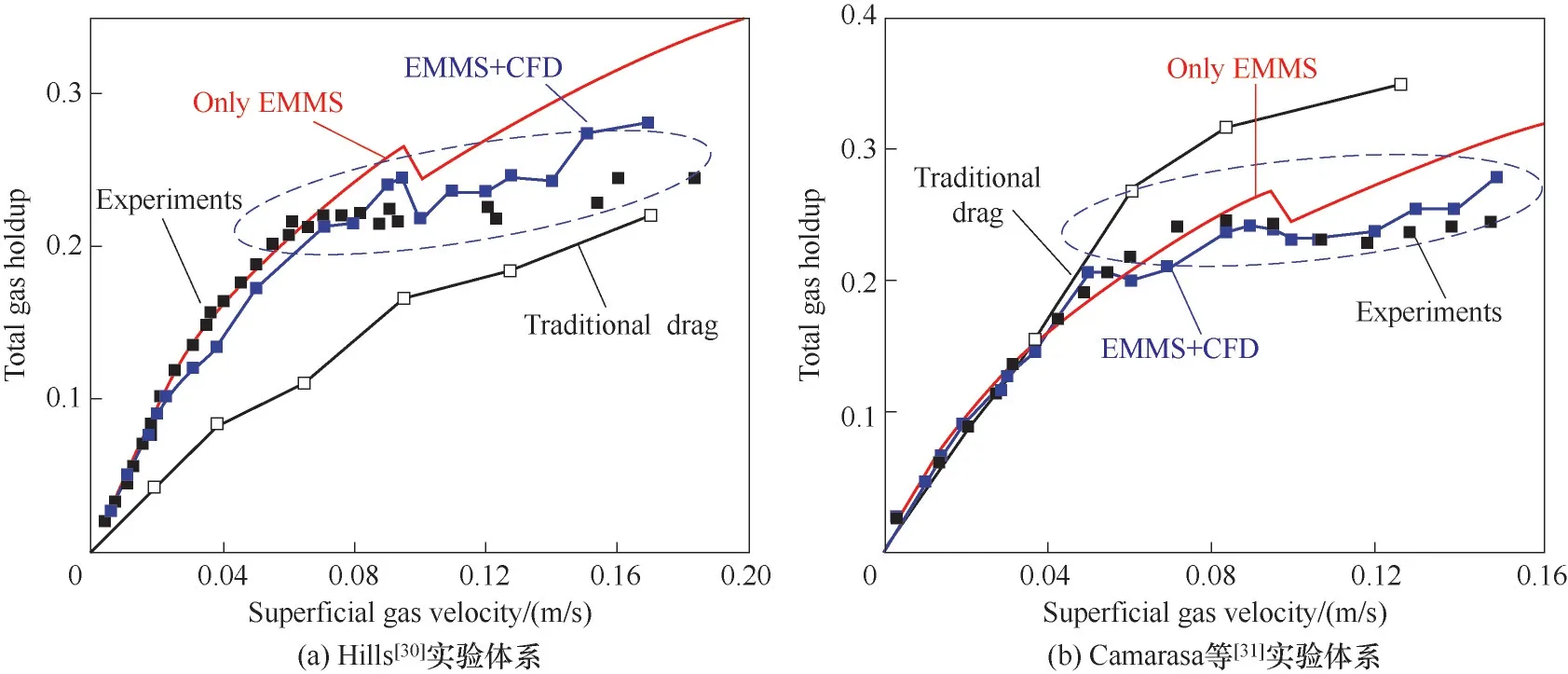
图4 高表观气速下总体气含率的平台现象[14]Fig.4 The shoulder of total holdup at high superficial gas velocity[14]

Guan 等[33]建立了不同操作模式下的介尺度曳力模型，应用于不同操作模式的鼓泡塔的模拟，在总体气含率及气含率分布方面获得很好的预测效果。Zhou 等[34-35]将介尺度曳力模型拓展应用至含固体颗粒的浆态床模拟，表明低固含率下可以直接采用气液体系的介尺度曳力模型，而高固含率情况下需要针对性的发展气液介尺度曳力模型。Yan等[36-37]在常压空气-水体系的介尺度曳力模型的基础上，考虑气体密度、黏度或者表面张力的修正，应用于压力或者物性不同的鼓泡塔体系模拟。

上述工作将CD/db和整体宏观操作参数直接关联，然后应用至整个气液体系，称此类模型为“整体式介尺度曳力模型”。然而，在气液鼓泡体系内，尤其是处于湍流鼓泡区时，流动的时空非均匀性强烈，强烈的局部流动效应使得介尺度结构也呈现时空动态变化，致使有效曳力系数也将随之动态变化。因此，发展考虑局部流动效应的“局部式介尺度曳力模型”更为合适。蒋雪冬[28]首先尝试关联了CD/db和局部表观气速及表观液速的关系，然后将每个计算网格的表观速度代入得到计算网格的CD/db。Guan 等[29]计算了介尺度理论模型在不同表观气速下的气含率和CD/db，然后将气含率和CD/db一一对应，进而实现CD/db和计算网格内气含率的关联，如表1 所示。Guan 等[29]比较了不同曳力模型对鼓泡塔总体气含率、气含率和液速分布的预测，表明局部式介尺度曳力模型能进一步提高对液速的预测。

表1 气液体系介尺度曳力模型数学关联式Table 1 Mathematical correlations for the mesoscale drag model in the gas-liquid system

介尺度曳力模型的发展经历了从气固体系到气液及气液固体系、从整体式模型到局部式模型的发展历程。该曳力模型不含有可调参数，弥补了传统多流体模型丢失介尺度结构信息的缺陷，突破了传统方法的薄弱环节，从而极大地提高了多流体模型模拟的准确性。

3 介尺度群体平衡模型

聚并破碎核函数用于描述气泡聚并破碎过程动力学，是群体平衡模型的核心。介尺度群体平衡模型的思路如图5 所示，求解介尺度理论模型获得系统的结构参数以及基于结构分解的介尺度能耗。将结构参数代入简化群体平衡模型，可获得分散相粒径分布，进而得到基于该粒径分布的介尺度能耗。该介尺度能耗与介尺度理论模型得到的介尺度能耗应该相等，采用此物理限制条件确定聚并破碎速率。换而言之，将介尺度能耗作为系统聚并破碎过程的物理限制，用于改进传统聚并破碎核函数。体系的介尺度能耗是由稳定性条件决定的，因此改进的聚并破碎核函数也受稳定性条件的约束。

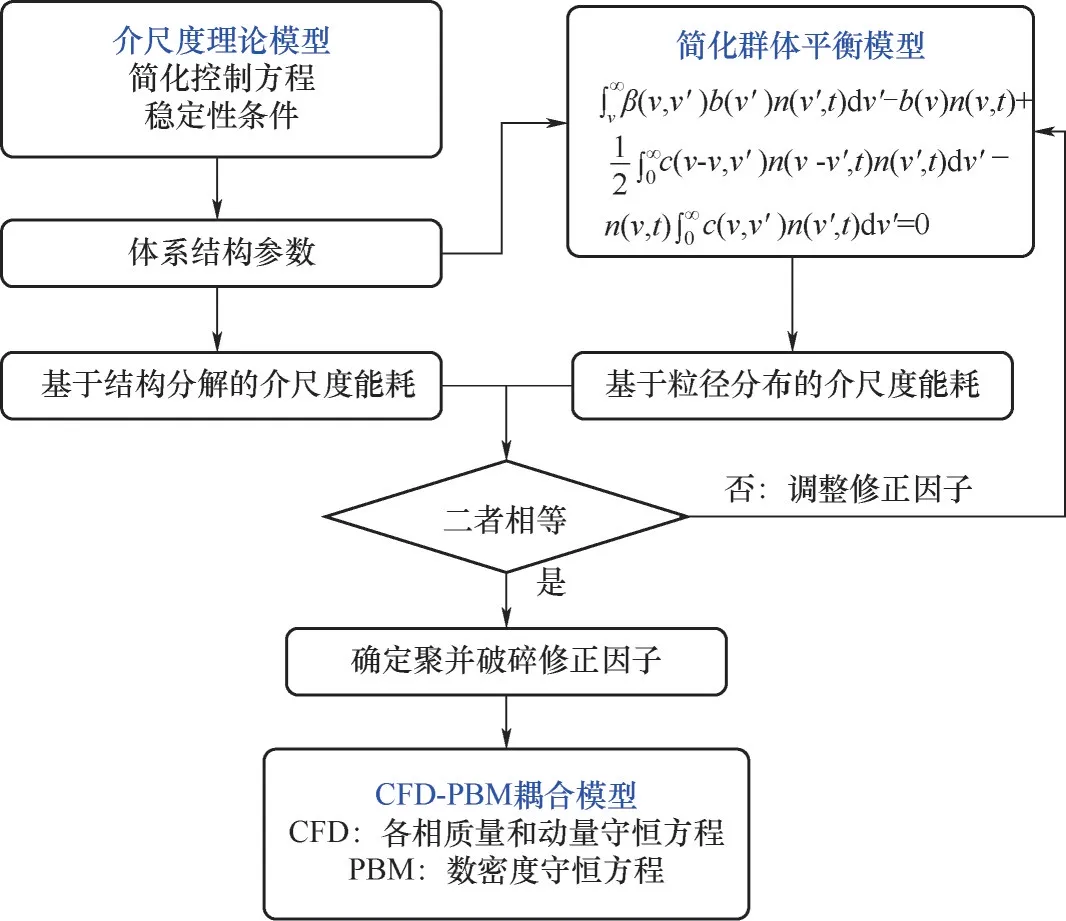
图5 介尺度群体平衡模型[38]Fig.5 Mesoscale population balance model[38]

Yang 等[38]以及An 等[39]针对鼓泡塔，确定了采用Luo-Svendsen 破碎模型分别结合Prince-Blanch 聚并模型以及Luo 聚并模型的聚并修正因子，并建立了修正因子与表观气速的关联。如图6 所示，无论是Luo 聚并模型还是Prince-Blanch 聚并模型，采用基于介尺度理论模型的修正因子均能给出较好的气泡粒径分布，而原始模型或者采用Bhole 修正因子时的准确性对聚并模型有依赖性，适用性有限。王珏等[40]发现介尺度群平衡模型能更好地预测鼓泡塔内不同高度的气泡粒径分布和轴向液速。An等[39]将介尺度群体平衡模型应用至浆态床的气泡粒径分布模拟，并分析了固体颗粒对物性、液膜排干时间和湍流的影响，表明固体颗粒对湍流的衰减作用是改变气泡粒径分布的主要原因。

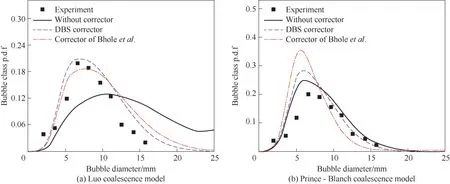
图6 Luo-Svendsen破碎模型结合不同聚并模型时的气泡粒径分布预测[38]Fig.6 Bubble size distribution predicted by different coalescence model combined with Luo-Svendsen breakage model[38]

聚并破碎过程复杂，影响因素很多，造成现有的聚并破碎核函数需要针对不同操作条件、装备结构以及物化性质调整模型参数。介尺度群体平衡模型采用介尺度能耗对群体平衡模型进行了额外的物理限制，避免了随意调整模型参数，提高了对粒径分布的预测。

4 模型的应用

介尺度曳力和群体平衡模型已经拓展应用至气升式环流反应器、气液搅拌槽、液液乳化设备等不同工艺过程核心设备的模拟、优化以及放大。气升式环流反应器包括内环流反应器和外环流反应器两类。根据下降管内气体存在形态划分为三种流动形态[41]：无气体携入流域、气体携入而不循环流域以及气体完全循环流域。能模拟下降管内气体的形态是准确预测环流反应器流动规律的前提。Xu等[42]以及张佳宝等[43]将局部式介尺度曳力模型应用至内环流反应器，表明模型能很好地模拟下降管内气体形态以及气含率，而其他曳力模型预测结果表明下降管内未观察到气体，处于无气体携入流域，与实验现象不一致。Jiang 等[44]将该介尺度曳力模型应用至外环流反应器，表明模型能很好地预测上升管内的总气含率、局部气含率、液速和气泡速度。

气液搅拌槽是一类带机械搅拌的气液反应器，根据气体的运动形态划分为气泛区、载气区和完全循环区三种流型[45]。肖颀等[46]比较了整体式介尺度曳力模型和Schiller-Naumann 曳力模型在三种流型下搅拌桨附近排出区的流动预测效果。表明在完全循环区流域，Schiller-Naumann 曳力模型明显低估桨叶下方的气含率，而介尺度曳力模型能更准确描述此流域的槽内流动情况。李新菊等[47]将局部式介尺度曳力模型应用至气液搅拌槽，并与Tomiyama曳力模型预测结果相比较。模拟结果表明Tomiyama 曳力模型只能可靠地预测低转速(140 r/min，280 r/min)条件下循环区局部气含率，而介尺度曳力模型能适用于整个实验测量的转速范围。Guan 等[48]比较了整体式和局部式介尺度曳力模型、Brucato 曳力模型以及Schiller-Naumann 曳力模型在预测流型方面的可靠性，表明Brucato曳力模型预测的流域过渡提前，而Schiller-Naumann 曳力模型流域过渡延迟，而介尺度曳力模型能很好地预测不同操作条件下的操作流域。如图7 所示，在400 r/min的转速下，实验处于载气区，即气体在搅拌桨上方能有效分散，但气体不能被携带至搅拌桨下方，介尺度模型能给出准确的流型，而Schiller-Naumann模型预测是气泛区，气体在搅拌桨上方未得到有效分散。在600 r/min 的转速时，实验处于完全循环区，即气体能带到搅拌桨下方形成循环，介尺度模型的预测确实有气体能携带入搅拌桨下方，处于完全循环区，而Schiller-Naumann 模型预测的是载气区流型，搅拌桨下方未观察到气体。

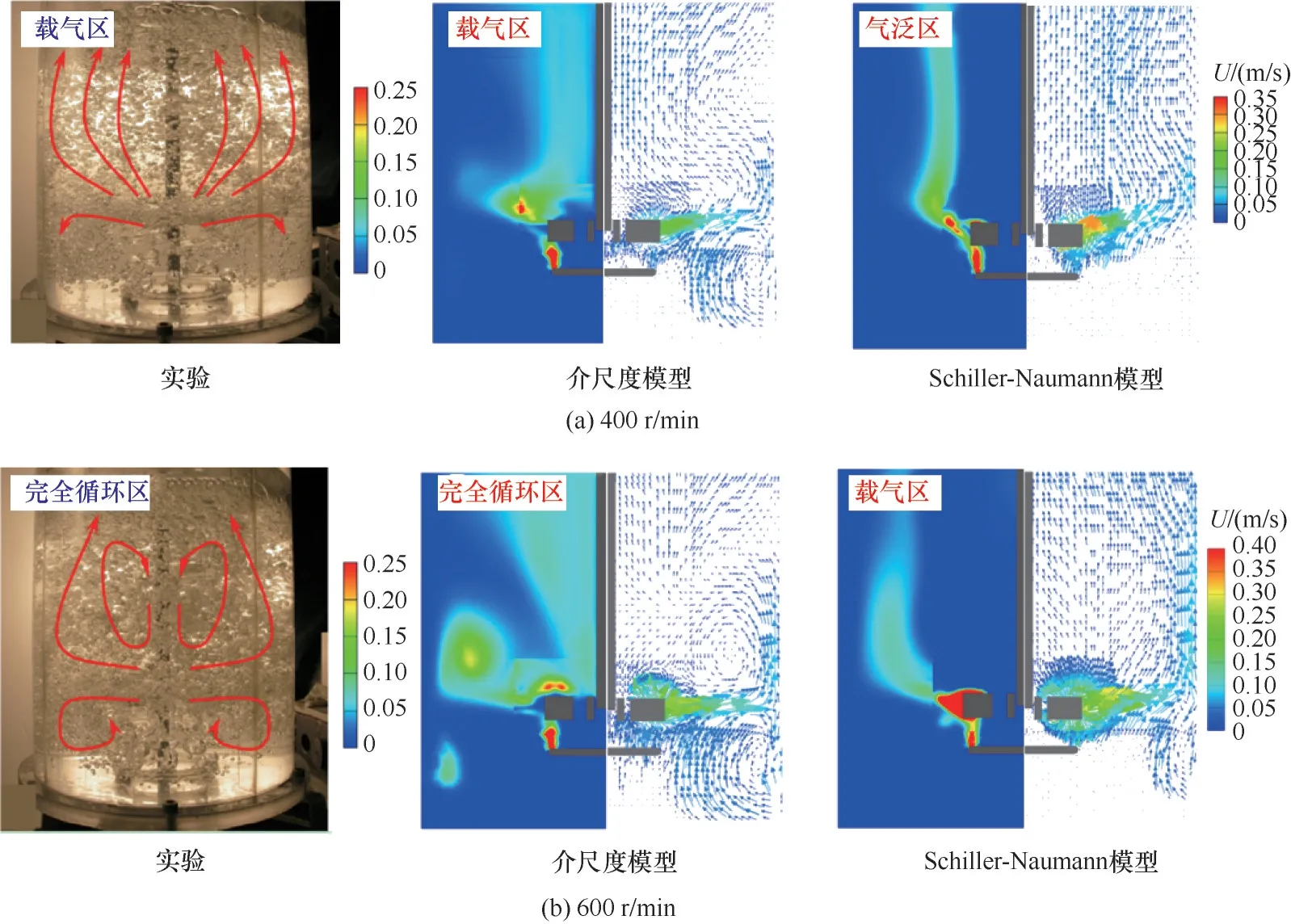
图7 气液搅拌槽操作流域的预测[48-49](模拟图左边：气含率云图；右边：气体速度矢量图)Fig.7 Predicted flow regime in gas-liquid stirred tanks[48-49](left:gas holdup contour;right:gas velocity vector)

介尺度群体平衡模型用于预测分散相粒径分布。Qin 等[50]以及Chen 等[51-52]将介尺度群体平衡模型拓展应用至转子-定子乳化设备，表明该方法能改善模型对不同操作条件下液滴尺寸分布、索特平均直径、中位直径以及跨度的预测。Chen 等[52]将介尺度群体平衡模型与表面活性剂在体相及界面上分配的输运模型相耦合，建立了跨层次的介尺度模型，揭示了相界面层次和设备层次介尺度结构的耦合机制，深化了对乳化过程流动-传递的科学认识。如图8 所示，仅考虑相界面层次或者设备层次的介尺度机制均明显高估液滴尺寸，而将两个层次的介尺度耦合起来将大幅度提高液滴尺寸分布的预测准确性，与实验结果更加相符。

图8 跨层次介尺度模型对液滴尺寸分布的预测[52][30%（质量）分散相，乳化剂0.1%（质量），转速9000 r/min]Fig.8 Prediction of droplet size distribution with levelcrossing meso-scale model[52][30%(mass)dispersed phase,0.1%(mass)emulsifier,rotational speed 9000 r/min]

5 结论及展望

相间作用力模型、湍流模型以及聚并破碎核函数用于描述微观的相内或者相间的相互作用对宏观流动的影响，这些封闭子模型直接决定了多流体模型模拟结果的准确性。本文首先概述了能量最小多尺度方法及其在气固流态化和气液多相流中的应用，然后总结了基于介尺度稳定条件的两类介尺度封闭模型(介尺度曳力模型和介尺度群体平衡模型)的构建方法，进而综述了这些封闭模型在流化床、鼓泡塔、气升式环流反应器、搅拌槽、转定子乳化器等多相流设备中的应用，主要结论如下。

（1）从介科学角度发展介尺度物理模型，解析多相流非均匀结构演化的控制机制，并将介尺度模型与CFD 相结合，为认识多相流复杂性提供了新思路以及新途径；

（2）对多相体系进行尺度分解以及控制机制分解，建立不同控制机制竞争协调的介尺度稳定性条件，能深入认识体系宏观流域过渡的物理机制，比如气固体系的噎塞现象，气液体系向湍流鼓泡区的过渡；

（3）基于稳定性条件约束的介尺度曳力模型和介尺度群体平衡模型由于弥补了介尺度结构信息，突破了传统模型的薄弱环节，使得模型在不含有可调参数的情况下，能够准确预测流场、流域过渡以及分散相粒径分布等；

（4）介尺度封闭模型在流化床、鼓泡塔、气升式环流反应器、搅拌槽、转定子乳化器等多相流设备的应用取得很好的效果，大幅度提高了CFD 的预测能力。

基于以上文献综述和总结，建议未来的研究方向应包括以下方面。

（1）介尺度稳定性条件的基础科学问题：稳定性条件反映了控制机制间的竞争协调，数学上表达为多目标优化，如何求解该数学问题，如何分离体系的控制机制，是否存在普世性的控制机制建模方法，气液及气固体系的稳定性条件是否存在相似性，相界面层次的稳定性条件如何构建，是否可能通过稳定性条件实现跨层次的耦合。

（2）气液多相湍流包括剪切湍流产生机制和气泡诱导湍流产生机制，发展气液体系的介尺度湍流模型，并实现该模型的介尺度稳定性条件与CFD 的结合是未来的重要研究方向。

（3）目前通过介尺度封闭模型实现稳定性条件和CFD 的结合，进一步探索其他的动态、稳态或者半动态的结合方式。

（4）研究介尺度封闭模型和DNS、过滤模型之间的数学物理关系，能否实现三者的有机统一。

（5）进一步强化介尺度模型与人工智能的结合。目前在介尺度封闭模型的关联方面实现了与人工智能的初步结合。在介尺度模型中的控制机制分离以及稳定性条件构建能否实现与人工智能的结合。

符 号 说 明

CD——曳力系数

db——气泡粒径，m

FD——平均曳力，N/m3

f——气含率

U——表观速度，m/s

u——速度，m/s

α——相含率

β——平均相间曳力系数，N·s/m2

ρ——密度，kg/m3

下角标

c——连续相

d——分散相