气液固流化床流动介尺度模型研究进展

马永丽，刘明言，2，胡宗定

（1 天津大学化工学院，天津 300350； 2 化学工程联合国家重点实验室（天津大学），天津 300350）

引 言

气液固三相流化床在化工及相关过程工业中有着广泛的应用[1-6]。但是，相对于单相流和两相流系统，第三相的加入，使得三相流动的时空结构更加复杂多变，给其模型化研究带来了更大的挑战，制约着系统的定量化设计和放大及工业应用。

20世纪60年代以来，研究者[5-6]建立了经典的气液固流化床的整体和局部流动机理模型。Bhatia等[3]首先建立了经典的气液固流化床流动行为的统一尾流模型，之后研究者[7-13]又建立了结构尾流模型、逐级分割处理模型、颗粒终端速度模型、飘移通量模型、四区模型、循环流模型等。这些经典的三相流动机理模型的建立，对于进一步了解三相流化床内的流动机理，定量化描述其流动行为奠定了基础。但是，这些经典的气液固流动模型没有很好地考虑三相流动的多尺度结构及其稳定性。三相流化床内存在着复杂的多尺度相互作用，主要包括：固体颗粒和流体间的微尺度相互作用等，气泡及其尾流或颗粒聚团与流体间的介尺度相互作用，以及整个流化床床层与床壁面或环境间的宏尺度相关作用等。原有模型忽略了三相流化床系统的多尺度流动结构及其稳定性，因而难以客观准确地量化描述系统行为，模型在预测能力和预测精度上受到限制。因此，为了实现对三相流化床系统流动行为全面而准确的刻画，需要引入考虑多尺度结构特征的新方法进行量化研究，以期抓住复杂问题的实质，进行更为准确的量化描述。基于能量最小多尺度作用（EMMS）原理的介科学方法[14]，着眼于多相流动系统的多尺度非均匀结构及其稳定性，从多尺度角度分析力平衡问题，并以悬浮输送能耗最小判断系统稳定性，从而为建立气液固流化床内三相流动的机理模型提供了新途径。

李静海[14]提出的气固两相流EMMS 模型能较好地描述气固两相流等复杂系统的非均匀结构及流动行为。EMMS模型采用变分型的多尺度分解方法将多相流动系统的非均匀结构进行尺度分解，分析其形成的两种主导机制，将主导机制之间的竞争与协调关系表达为数学上的“多目标变分”问题。目前应用基于EMMS的介科学方法建模的流动系统以两相（气固、气液和液固）流动体系为主[15-16]。EMMS模型通过量化分析控制流化床系统主导机制间的协调关系，如悬浮与输送能控制[17]、黏性与惯性控制[18]、不同气泡尺寸控制[19]等，揭示控制复杂流动行为的原因。Xu 等[20]通过分析气固流化床中的界面应力分布，表明密相颗粒团的界面应力远大于稀相中的界面应力。Yang 等[21]考察了气固流化床中的非均匀结构，得到了校正曳力系数，将该系数与双流体模型耦合，提高了CFD 模拟的准确性。考虑到多相流动系统的非线性和非稳态特点，后续的EMMS模型引入了气泡或固体颗粒的加速度[21-23]，用来描述气泡与固体颗粒所受到的不平衡力。Ge等[22]分析了气固流化床的固体颗粒的加速行为，建立了考虑颗粒加速度的EMMS 机理模型，并得到了流体催化裂化（fluid cracking catalyst，FCC）固体颗粒-空气系统中流型的分布图。Liu等[24]考虑了气液固流化床内复杂的多尺度流动结构特征，首次将源于气固两相流的能量最小多尺度作用原理应用于气液固流化床内的复杂流动行为的建模研究。近年来，研究者又进行了系统深入的研究，建立了三相流整体和局部介尺度机理模型，获得了较强的预测能力和较高的预测精度[25-29]。

本文针对目前气液固流化床流动机理模型的国内外研究进展进行综述。首先简要介绍早期建立的比较经典的描述气液固流化床内三相流动的机理模型，因为之后的气液固流化床流动介尺度机理模型的建立，也吸收了这些经典机理模型中有价值的观点或信息。之后，重点针对近年来建立的描述气液固流化床内复杂三相流动结构的介尺度机理模型进行分析和总结，主要包括：考虑三相流化床中气泡分散相和固体颗粒分散相加速度的整体三相流动介尺度机理模型[25-26]，可预测气液固膨胀流化床和循环流化床内三相流动轴向分布特性的介尺度模型[27-28]，以及定量描述气液固循环流化床内三相流动径向分布特性的介尺度模型等[29]，并指出目前存在的问题和需要进一步开展研究的方向。

需要指出的是，从描述三相流化床系统的基本守恒方程出发，开展计算流体力学数值模拟研究，也是解决三相流化床的定量化描述，实现其科学设计和放大的关键途径之一[30-34]。

1 经典机理模型

经典的气液固流动机理模型间有一定的顺承关系，模型的预测能力逐步深入，大致遵循了由起始的全床相含率等整体流动参数预测，到之后的三相流化床轴向或径向分布等局部流动参数的预测顺序，但是也相对独立。下面的模型介绍也依此关系展开。

1.1 统一尾流模型

Bhatia 等[3]将气液固流化床内的三相流动系统划分为气泡区、尾流区和液固流化区，如图1 所示。基于质量守恒和动量守恒定律，量化了固相和液相的连续性行为和动量守恒特性，同时，引入两个量化气泡尾流流动行为的关键参数，即尾流体积分数和气泡体积之比（k）、尾流相固含率与周围液-固拟均相的固含率之比（x），推导建立了统一尾流模型。

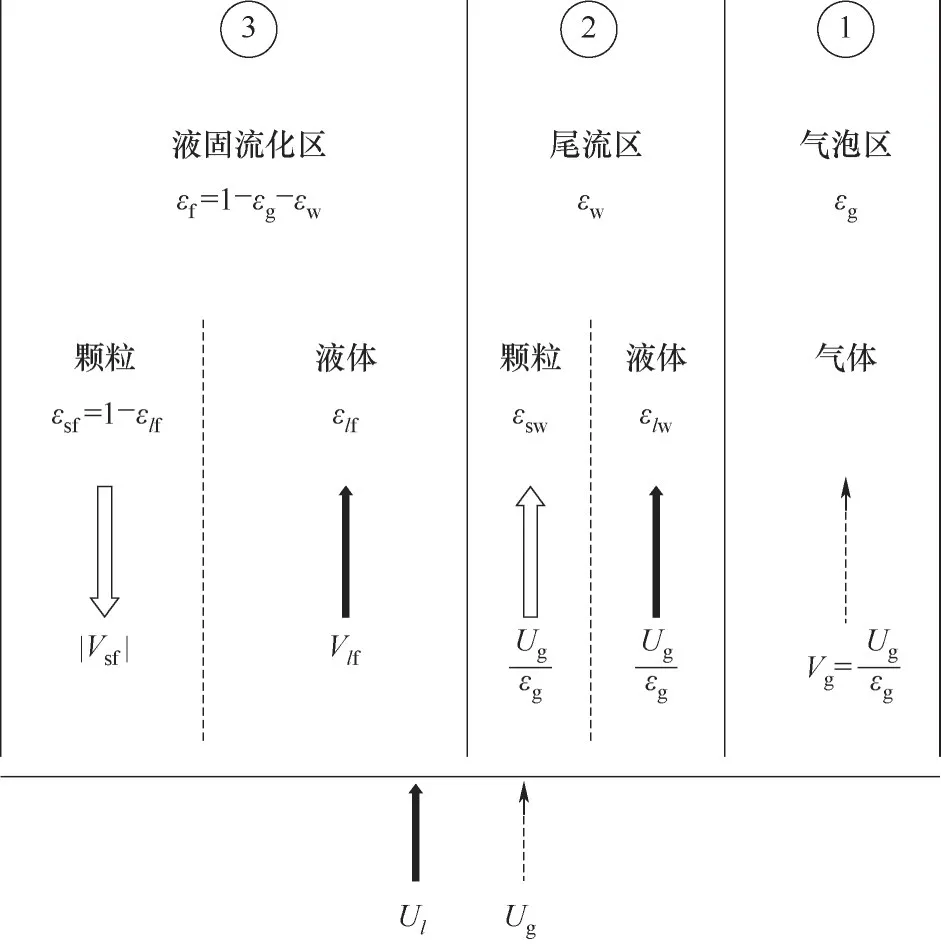
图1 气液固流化床流动的统一尾流机理模型[3]Fig.1 General wake model of gas-liquid-solid fluidized bed[3]

统一尾流机理模型能很好地预测气泡尾流的结构，但是模型引入的两个关键参数（x和k）的求解依赖于经验关联式，导致该模型对相含率预测的准确性很大程度上取决于两个关键参数的关联式的准确性。推得的模型方程如式（1）和式（2）所示。

液含率：

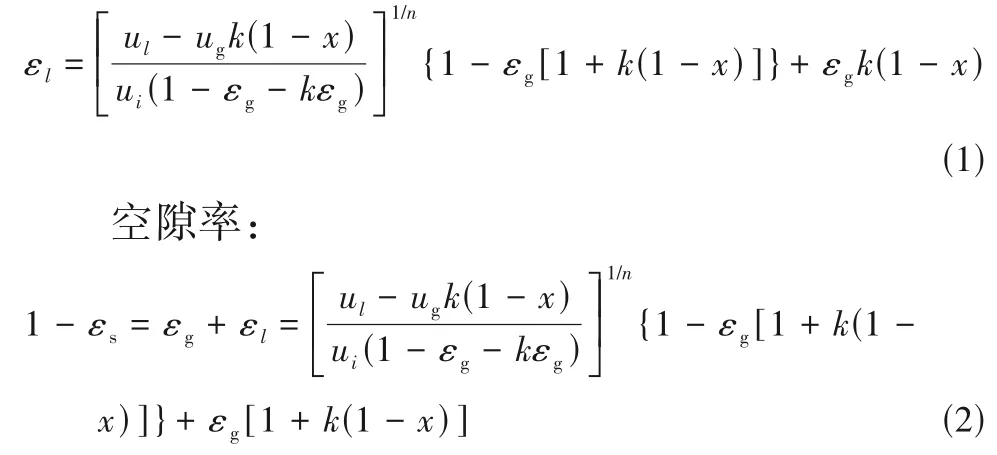
研究者对统一尾流模型引入的两个模型参数（x和k）的计算有不同的观点（表1）。例如，Efremov等[35]假设气泡尾流相的固含率为0，采用计算体积比k的经验关联式求得相含率和其他流动参数。为了减小经验关联式带来的误差，Fan等[43]通过实验研究了流动过程中气泡尾流的行为特点，发现气泡尾流体积与气泡体积的关系与数学上的锯齿波函数相吻合。Muroyama 等[44]总结了文献中关于这两个参数的报道。

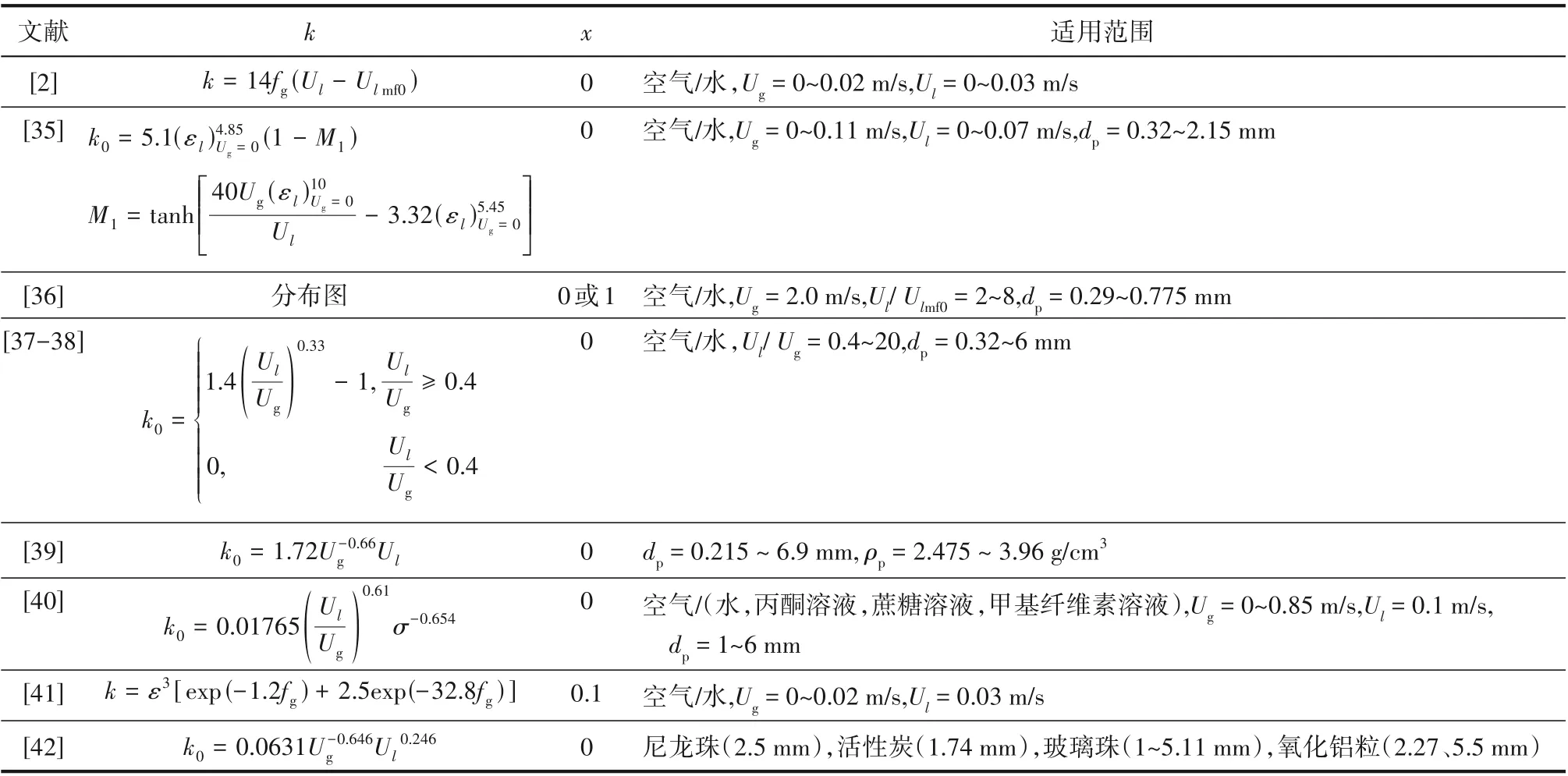
表1 统一尾流模型参数的经验关联式［3］Table 1 Empirical correlation of parameters general wake model［3］

1.2 结构尾流模型

统一尾流模型将气泡尾流中的固体颗粒与液体流化区中的固体颗粒相隔离，这与实际过程不符。为了解释三相流化床气泡尾流中固体颗粒的非封闭属性，Fan 等[7]假设三相流化床的床层收缩和固体颗粒混合等流体力学现象由气泡的基本尾流决定；将气泡基本尾流分为约束湍动尾流区（CTW）与剥落旋涡尾流区（SVW）；某种意义上，统一尾流模型中的尾流对应CTW 区；SVW 区会不断地剥落一定体积的固体颗粒旋流，进入次生尾流，并最后进入液固流化区；气泡尾流中旋涡周期性的脱落频率与其形成频率动态相等。基于这一机制，提出了结构尾流模型，如式（3）所示。

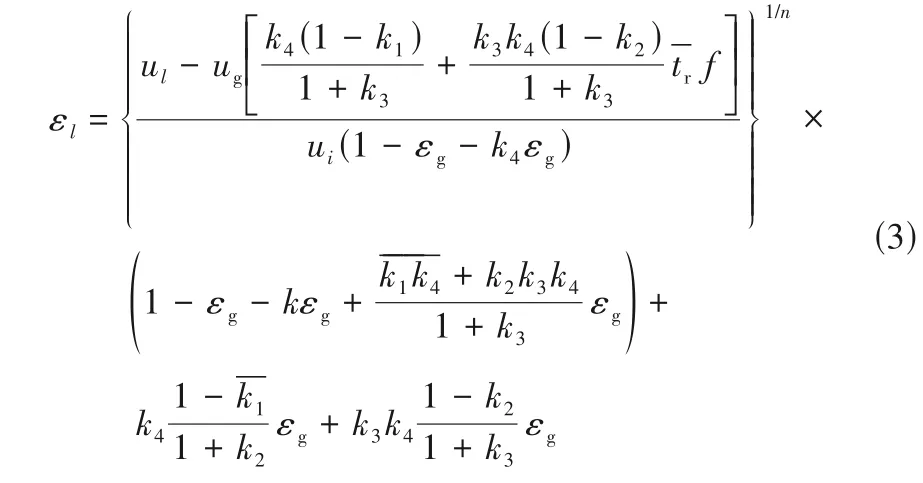
该模型也可以预测床层收缩等特性。但是，由于结构尾流模型的参数较多，公式过于复杂，很少应用。

1.3 逐级分割处理模型

Page 等[45]曾认为气泡尾流相中，旋涡的周期性形成与剥落行为导致了气液固流化床自由空间区的轴向不均匀结构。El-Temtamy 等[8]针对自由空间区的固体颗粒夹带，提出了一个逐级分割处理模型，即将轴向过渡段分割为不同的级。模型假设每一级中，固体颗粒由气泡尾流夹带，上升过程中固体颗粒不断地被剥落，进入周围的液固相流化区，而后在液固流化区沉降。连续两个尾流剥落之间的时间间隔内，气泡运动的距离定义为一个剥落单元高度，分割的级高度等于尾流剥落单元高度。各级的序号从自由空间区的顶部向下面的流化床界面顺序排列。求解该模型时，列第N级的固体颗粒质量守恒方程。假设气泡尾流相和液固相的固含率已知，可以得到第N级的固体颗粒含率为式（4）。计算时从第一级开始，向下逐级计算其（εs）N，直到其数值等于或大于流化床主体区内的固含率为止。

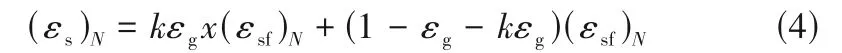
1.4 终端速度模型

气液固流化床中固体颗粒的终端速度应与液固流化床中固体颗粒的终端速度不同。占主导地位的气泡行为会间接影响气液介质中颗粒的终端速度。Jean 等[9-10]建议除了考虑颗粒所受的液相曳力和有效重力（重力-浮力）之外，还应增加一个考虑颗粒-气泡间相互作用影响的相间作用力，提出了计算三相流化床中固体颗粒终端速度的模型，如式（5）所示。

式中的U′l对应的是气液介质中的颗粒终端速度。研究表明，在含有玻璃珠的三相流动体系中，当固体颗粒的直径大于临界尺寸460 μm时，其终端速度随表观气速的增加而降低，当固体颗粒的直径小于临界尺寸460 μm时，其终端速度与表观气速无关，保持为常数。

1.5 漂移通量模型

在多相流研究过程中，一般有两种方法描述不同相间的相互作用，一种是相对速度或滑移速度（相对于运动速度较慢一相的速度），另一种是漂移速度或漂移通量（相对于所有各相的体积平均速度）。漂移速度源于气液两相流系统的研究，Chen等[11]将漂移速度直接延伸于分析气液固三相流化床气泡的运动，提出了漂移通量模型。同时切断三相流化床的气流与液流，将动态塌陷的三相床从下往上依次分为：填充床区、沉降区、三相流化床区和气液分离区。基于质量守恒定律分析，建立了描述气泡上升速度的漂移通量模型方程，如式（6）所示。

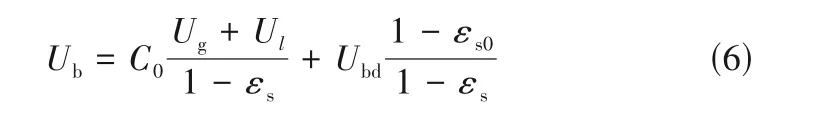
式中，C0为一经验常数，取值与三相流化床内的流型有关（在低表观气速下或较高表观液速下，三相流化床的流动处于气泡分散流区，C0=1；在高表观气速下，流动状况处于气泡聚并流区或节涌流区，C0数值只能通过实验确定）;Ubd为三相流化床区中与液固混合物逆流的气泡漂移速度；εs0为无气液流动时，气泡边界下面的颗粒平均固含率。

1.6 四区模型

鉴于统一尾流模型认为气液固流化床是由气泡区、气泡尾流区和液固拟均相区组成，只能预测三相流化床的平均相含率，胡宗定等[12]在此基础上，引入新的参数——液涡因子，将液固区进一步划分为液涡区和纯粹液固流化区，提出了预测三相流化床相含率的四区模型。基于该模型可以预测三相流化床内的平均相含率，以及相含率的轴、径向分布。不过，模型中的液涡因子、气泡尾流与液固混合相的固含率之比需通过实验获取。

1.7 循环流模型

Morooka 等[13,38,46]发现，与气液鼓泡塔的径向流动类似，气液固流化床内的气含率和液体流速也呈现出床中心处向上而在床壁面处向下的径向分布规律。基于这一现象，Morooka 等[13]引入气含率的径向分布函数关联式，并假设三相流动系统中的湍流运动黏度在湍流区内恒定不变，提出了用于预测稳态三相流化床中固体颗粒缝隙液体速度径向分布的循环流模型，如式（7）所示。

式中，Vlw为流化床壁面处的流动线速度;Dc为流化床直径;υT为湍流运动黏度;υl为液体运动黏度。

可以看出，液体速度在流化床中心轴线上达到最大值时，边壁上达到最小值。

这些流动机理模型的建立，初步实现了气液固流化床内复杂三相流动行为的量化描述。下面简要介绍近年来基于能量最小多尺度作用原理（EMMS）的介尺度方法而建立的气液固流化床三相流动机理模型。

2 基于能量最小多尺度作用原理的气液固流动介尺度机理模型

由于气液固流化床的操作模式较多，这里仅对液相为连续相、气相和固体颗粒相为分散相或离散相的三相流化床流动机理模型进行综述。其他诸如气相为连续相、液相和固体颗粒相为离散相的三相流化床操作模式的介尺度模型亦有研究，可以参考文献[47]。

2.1 气液固流化床全局流动介尺度机理模型

Liu 等[24]最早引入介科学方法，对气液固流化床内的复杂流动行为建立了EMMS 全局流动机理模型。该模型将三相流体系分解为3 个子系统，即气泡相、液固拟均相以及相界面作用相，如图2 所示。将气液固流动系统中的多尺度表达为：微尺度作用——固体颗粒与液体流化介质之间的相互作用；介尺度作用——液固相与气泡之间的相间相互作用；宏尺度作用——三相流化床系统与床壁面等边界间的相互作用。对于宏观流化床系统忽略宏尺度作用。

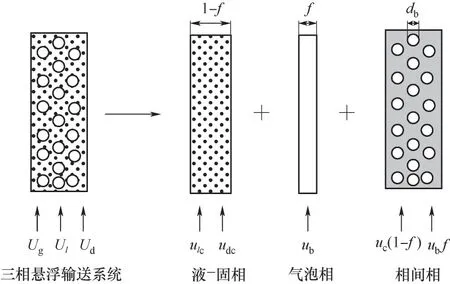
图2 气液固流化床系统的多尺度分解[24]Fig.2 Resolution of suspending and transporting subsystem of gas-liquid-solid fluidization system[24]

2.1.1 建立模型需要解决的关键问题 建立模型时，需要考虑一些关键问题，包括：（1）不同尺度的相间相互作用的多尺度分析及表述，表达为基于质量守恒和动量守恒推导得到模型方程；（2）基于能耗分析的稳定性判据的建立，表述为主导机制间的竞争协调关系（提出了三相流动系统中的两种主导机制，即固体颗粒倾向于停留在势能较小的位置，流体倾向于通过阻力较小的上升通道）；（3）特征尺度（最大气泡尺寸）的分析及表达。将三相流化床的几个关键问题进行数学描述，即得到描述气液固流动行为的介尺度数学模型的框架，如图3所示。

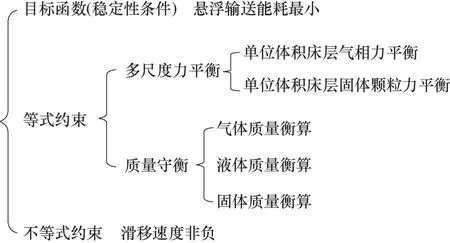
图3 气液固流化床流动行为的介尺度机理模型框架Fig.3 Mesoscale model framework of flow behavior in gasliquid-solid fluidized bed

两种机制的竞争与协调关系体现在目标函数这一稳定性条件上。通过求解，使目标函数系统的悬浮输送能最小，从而得到各流动参数的具体数值。

2.1.2 模型验证 图4给出了氮气-水-玻璃珠三相流化床系统中相含率的介尺度流动机理模型计算值与实验数据的比较。气含率的预测值稍大于实验值，其余预测结果与实验值吻合较好。气含率预测值偏大的原因与采用的气泡直径预测经验关联式源自于气液鼓泡塔有关。液含率的模型预测值与统一尾流模型的预测值接近[3]。图5表明，介尺度流动机理模型也可以预测空气-水-玻璃珠三相循环床及输送床相含率随操作条件的变化规律。

图4 氮气-水-玻璃珠流化床相含率的流动介尺度机理模型预测值与实验值的比较[3,24,48-49]Fig.4 Comparison between experimental data and model predictions of phase holdups in nitrogen-water-glass beads fluidized beds[3,24,48-49]

图5 空气-水-玻璃珠循环床及输送床相含率的介尺度流动机理模型预测值与实验值的比较[24,50-52](dp=0.405 mm,ρp=2500 kg/m3,D=0.14 m,Ug=0.018 m/s,Ud=0.0017 m/s)Fig.5 Comparison between experimental data and mesoscale flow model predictions of phase holdups for air-water-glass beads circulating and transport beds[24,50-52](dp=0.405 mm,ρp=2500 kg/m3,D=0.14 m,Ug=0.018 m/s,Ud=0.0017 m/s)

建立的三相流化床介尺度机理模型将气液固流化床的多尺度力平衡分析、质量守衡分析以及能耗分析有机结合，各种相间相互作用得以较合理考虑，其特点为:（1）考虑了气液固流化床系统的多尺度结构特征及其稳定性；（2）可以预测气泡直径；（3）不含任意参数或可调参数；（4）不含复杂微分方程式；（5）应用各向同性湍流理论及气泡破碎和聚并动力学描述三相流化床的气泡尺寸。

但是，该模型还需要进一步完善。存在的问题及需关注方向是：（1）忽略了气泡尾流的作用；（2）忽略了宏尺度作用（例如，流化床直径的影响）；（3）气泡大小及运动行为的描述有待进一步理论化；（4）气固间接相互作用的描述有待完善；（5）三相流化床的轴向和径向流动机理模型有待建立；（6）与数值模拟方法相结合预测三相流动态行为等有待开展。

2.2 考虑气泡尾流相的气液固流化床全局流动介尺度机理模型

在Liu 等[24]工作的基础上，Jin[25]考虑了气液固流化床中的气泡尾流相，如图6所示，建立了考虑气泡尾流相的气液固流化床全局介尺度机理模型。Jin[25]提出的介尺度机理模型的建立步骤为：（1）根据流动现象将流动体系划分为多个尺度；（2）建立不同尺度的稳定性条件以及不同尺度之间的关联式；（3）判别控制稳定流动结构的主导机制和不同主导机制之间的协调关系，制定变分标准，建立稳定性条件；（4）基于稳定性条件耦合守恒方程。

图6 基于不同尺度考虑气泡尾流的气液固流化床中悬浮和输送子系统的分解[25]Fig.6 Resolution for suspending and transporting subsystem in three-phase system based on different scales considering bubble wake[25]

图7为空气-水-玻璃珠三相循环流化床及输送床固含率模型计算值与实验数据的比较。相比于图5（a）的预测结果可以看出，该考虑气泡尾流相的介尺度机理模型可以在一定程度上提高三相EMMS全局模型的预测准确性。

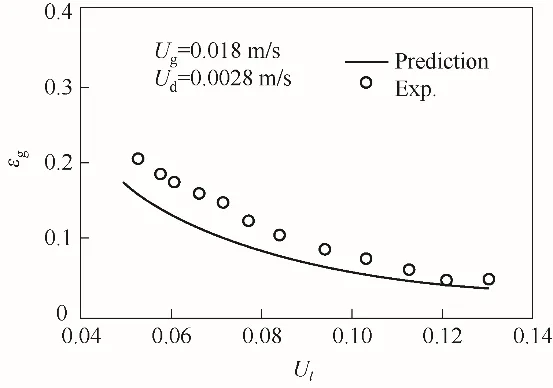
图7 空气-水-玻璃珠循环床及输送床固含率的流动介尺度模型与实验的比较[25,50-52](dp=0.405 mm,ρp=2500 kg/m3,D=0.14 m,Ug=0.018 m/s,Ud=0.0017 m/s)Fig.7 Comparison between experimental data and mesoscale flow model predictions of solid holdup for air-water-glass beads circulating and transport beds considering bubble wake[25,50-52](dp=0.405 mm,ρp=2500 kg/m3,D=0.14 m,Ug=0.018 m/s,Ud=0.0017 m/s)

但是，三相流动的复杂非稳态特征使得作用在固体颗粒与气泡表面的力处于非平衡状态。为进一步提高模型的预测准确性，需要考虑加速度项，以进一步完善该机理模型。

2.3 考虑分散相加速度的气液固流化床全局流动介尺度机理模型

在Liu 等[24-25]的介尺度机理模型研究的基础上，Ma 等[26]考虑了气泡和固体颗粒的加速行为，在动量守恒方程中引入了气泡与颗粒的加速度项，如式（8）和式（9）所示，建立了改进的三相流化床流动介尺度机理模型，可以更准确地预测气液固膨胀床的全局三相流动行为。

气液固流化床的系统分解示意如图8所示。

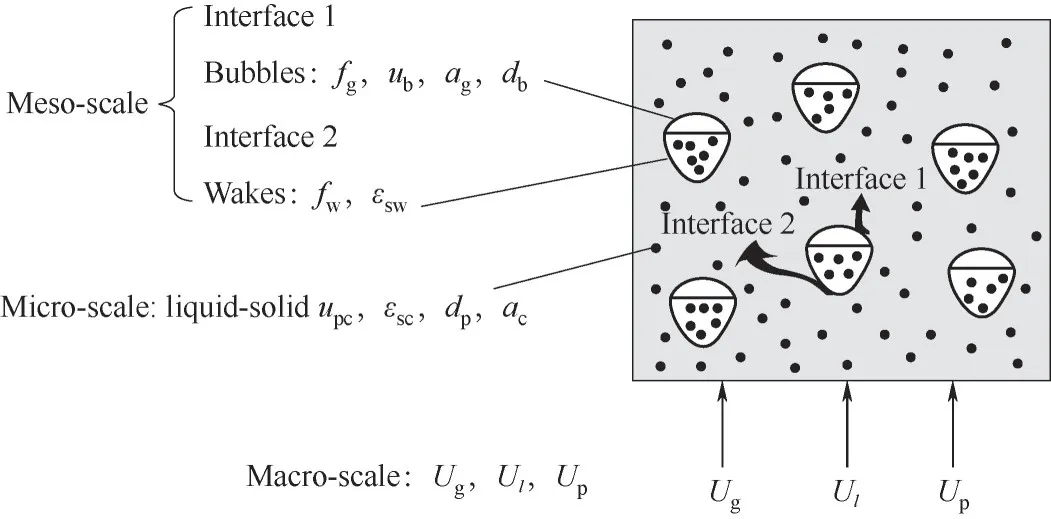
图8 考虑气泡和颗粒加速度的气液固流化床中的流动子系统[26]Fig.8 Resolution of the gas-liquid-soild fluidization system based on different scales when considering bubble and solid particle accelerations[26]

根据动量守恒定律，可得到固体颗粒和气泡每一相的动量衡算方程：

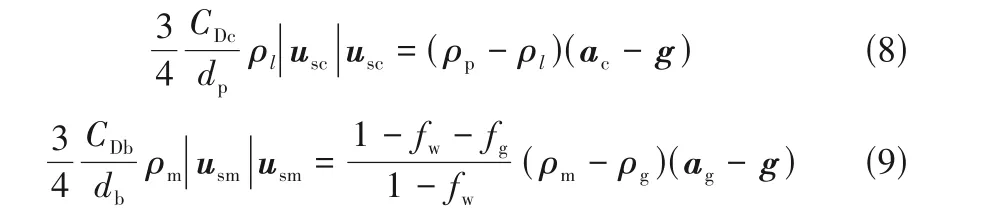
Ma 等[26]基于改进的三相流化床流动介尺度机理模型，预测了三相膨胀床的流动参数。相比于其他机理模型，改进的介尺度机理模型能够预测气体进入时的床层收缩现象，而包括Jin[25]等的其他两个模型不能预测床层收缩现象，如图9所示。同时，改进的介尺度机理模型对床层平均空隙率和固含率的预测结果与实验值更接近。

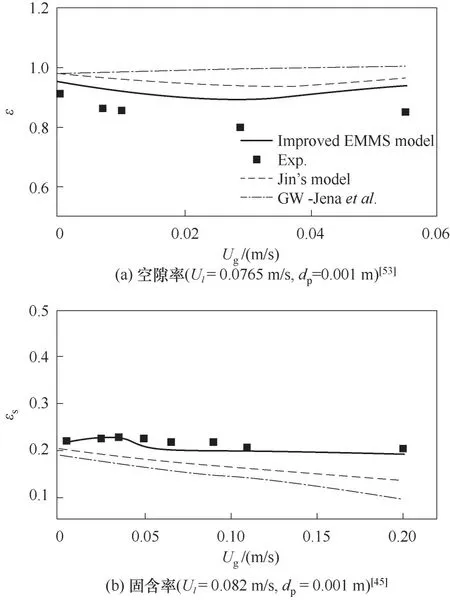
图9 三相膨胀床内相含率的模型预测值与实验值比较[26]Fig.9 Comparison between model predicted value and experimental value of phase holdup in three-phase expanded bed when considering bubble and solid particle accelerations[26]

需要说明的是，多相流动过程是一个复杂的非平衡非稳态过程。分散相加速度机理模型中的加速度表征的是系统偏离动态平衡状态的程度，计算的是一个全局平均值，加速度会随着操作条件的变化而改变。

2.4 三相流化床轴向流动介尺度机理模型

掌握气液固流化床内三相流动特性的轴向分布规律对于流化床反应器的设计、操作和控制十分重要。目前气液固流化床内的三相流动特性的轴向分布模型，多是基于沉降-扩散理论[54-56]，而且大多适用于泥浆鼓泡床体系，主要集中在对固体颗粒受阻沉降速度（vp）和其扩散系数（Ep）的研究，如表2所示。

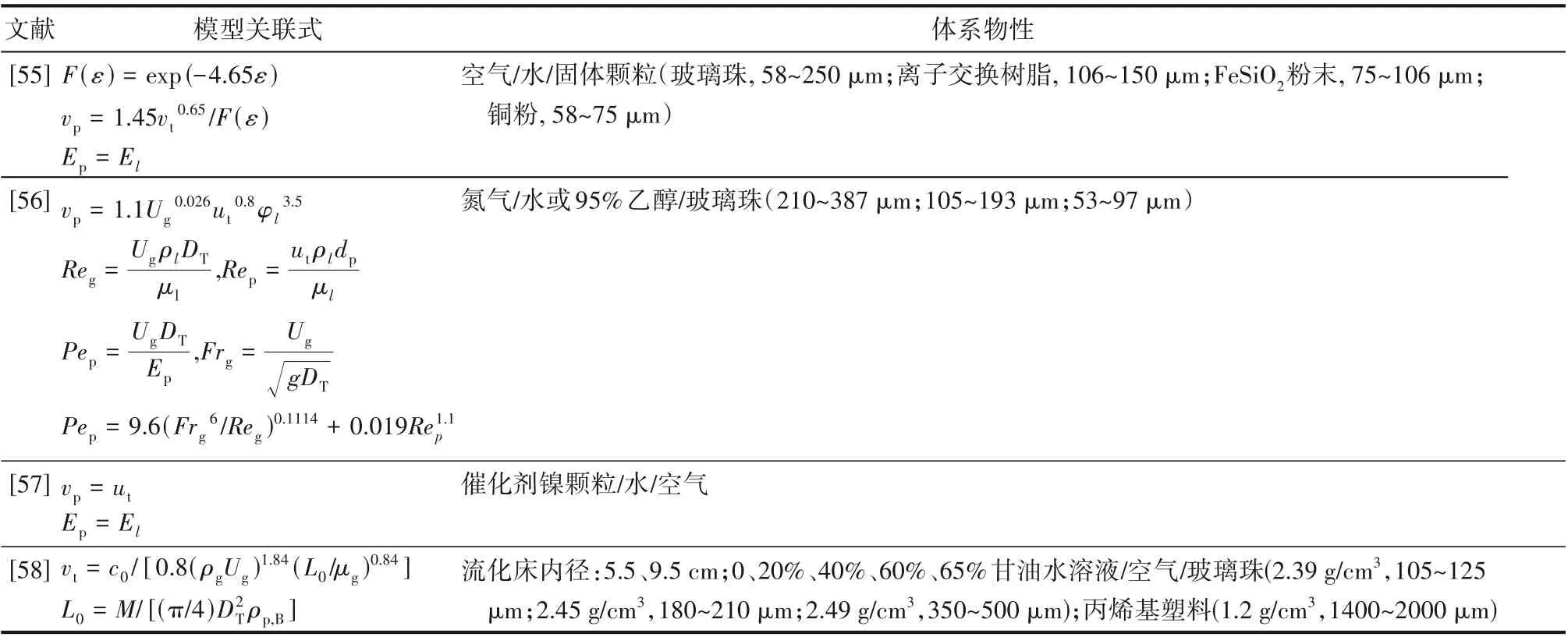
表2 沉降-扩散模型中的经验关联式Table 2 Empirical correlations in settlement-diffusion models

Matsumoto 等[59]基于“混合长理论”，将轴向滑移速度与固体颗粒扩散系数相关联；同时，修正固体颗粒沉降速度，提出了改进的一维沉降-扩散模型，预测了泥浆床内固含率的轴向分布。Tsutsumi 等[60]基于气液固膨胀床中的气泡尾流对固体颗粒的夹带特性，提出了尾流夹带模型。在气泡尾流的形成过程中，气泡底部的流动区域不断从周围液固相中累积物质，形成尾流；当气泡尾流的尺寸增加到临界值时，尾流相逐渐将固体颗粒以旋涡的形式剥落，导致固含率的轴向不均匀分布。

与三相膨胀床相比，对三相循环流化床轴向机理模型的研究很少。韩社教等[61]基于三相循环流动系统中颗粒团的沉降-扩散行为，建立了轴向模型。但是，引入了较多的经验式或需要通过实验获取的模型参数，并且大多只能预测固体颗粒的特性。

李静海[14]提出的基于EMMS 原理的介科学方法也为三相流化床的轴向复杂流体力学的模型化提供了新思路。

2.4.1 三相膨胀床轴向流动介尺度机理模型 在气液固膨胀床中，气泡尾流夹带的固体颗粒补充了固体颗粒的向上流动通量[53]，气泡尾流的这种行为使三相膨胀床形成不均匀轴向流动结构[62]。尾流对固体颗粒的夹带过程如图10所示。

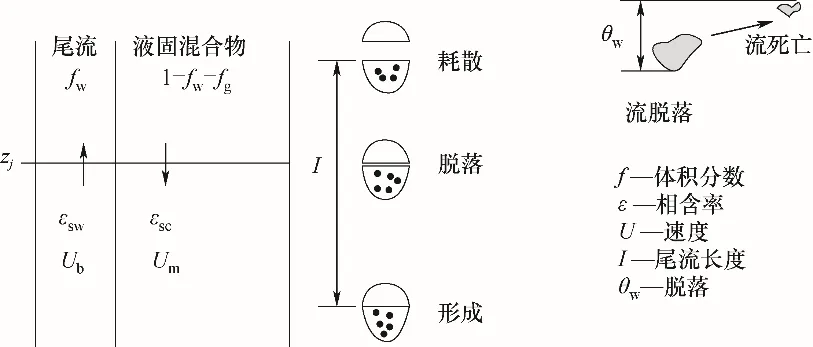
图10 气液固膨胀床中的尾流脱落过程[60,62]Fig.10 Bubble wake shedding process in gas-liquid-solid expanded bed[60,62]

根据三相膨胀床的流动特点，可将气液固膨胀床的轴向区域划分为分布器区、流化床主体区，以及自由空间区。这三个区的流体行为差异较大：分布器区的流动行为受分布器的设计，气体、液体以及固体颗粒的物性影响；流化床主体区的流体力学参数呈现均匀的轴向分布，其高度取决于操作液速和固体颗粒的物性参数；自由空间区的流动结构复杂，存在一定的轴向分布。由于分布器区的流动尚未达到稳定状态，因此，该区域不作为建模考察的内容。将自由空间区进一步划分为两个段或区，分别是轴向过渡段和气液分离段，如图11所示。密相的流化床主体（段）和过渡区包含气、液、固三相；气-液分离区仅包含气、液两相。存在于过渡区的非均匀轴向结构是机理建模考察的主要内容。

图11 气液固膨胀床轴向流动结构的多尺度分解[27]Fig.11 Multiscale resolution of axial flow structure of gasliquid-solid expanded bed[27]

以上述内容为基础，Ma 等[27]基于能量最小多尺度作用原理，将颗粒的轴向沉降-扩散特性进行介尺度建模，得到了三相膨胀床流动行为的轴向介尺度模型。建模过程中，首先在三相流化床轴向过渡区某一截面上，采用和全局建模类似的方法建立介尺度机理模型，然后再沿轴向积分，得到膨胀流化床流动行为的轴向分布介尺度模型。

受尾流流动行为的发展限制，所建三相膨胀床轴向流动介尺度模型中的尾流相固含率的计算仍然依赖于经验关联式，因此，模型的使用范围受限。

对所建的三相流化床轴向流动介尺度模型进行了三相膨胀床系统条件下的轴向流动参数实验验证和预测研究。图12 显示了三相膨胀床[63]中流动参数（fg，εs，εl，ub，db）的轴向分布。在密相主体区，图12（a）表明参数fg、εs、εl保持不变。在过渡段，随着轴向位置的增加，固含率降低，液含率呈指数形式增加。与Kato 等[62]的轴向模型相比，轴向流动介尺度模型与实验数据更接近。基于该实验体系的数据得到的关联式[64]的预测结果见图12（a）内嵌图。该结果与轴向流动介尺度模型的预测结果均表明，气含率首先呈现小幅度降低而后逐渐增加。气含率在初始阶段的减小是由两个因素引起的：首先，在轴向高度增加的初始阶段，湍动程度缓慢增强，促使气泡相互接触；其次，过渡段的底部区域的固含率相对较高，导致液固流区的黏度增加。这两个因素均有利于气泡的聚并变大，导致气含率降低。但是，随着轴向高度的继续增加，湍动强度快速增强，液体对气泡表面施加了一个比较大的剪切破坏力，导致气泡破裂而变小，气含率增加。此外，气泡直径的减小会增大气泡受到的曳力，即上升阻力增加，导致其速度下降。图12（b）验证了上述分析，气泡速度和直径均先增加后下降。

图12 气液固膨胀床中的流动参数的轴向分布[62-63]（Ul=0.0117 m/s，Ug=0.0128 m/s，dp=0.00025 m，ρp=2500 kg/m3，ρl=1000 kg/m3，ρg=1.2 kg/m3）Fig.12 Axial distribution of flow parameters in gas-liquidsolid expanded bed[62-63]

2.4.2 三相循环流化床轴向流动介尺度模型 相比于气液固膨胀床，气液固循环流化床中的气泡较小且分布均匀，对颗粒的夹带作用较弱，但在流动过程中，三相循环流化床中有裸眼可见的颗粒聚团产生的絮状物（也称团聚物）。因此，Ma 等[28]基于介尺度颗粒团流动系统的子系统分解（图13），建立了相应的轴向流动介尺度机理模型。计算结果表明，模型可预测循环流化床中的轴向流体力学行为。

图13 气液固循环流化床流动系统的介尺度子系统分解[28]Fig.13 Mesoscale subsystem resolution of gas-liquid-solid circulating fluidized bed flow system[28]

在气液固循环流动体系[65]的操作条件下，图14显示了轴向流动介尺度模型预测与实验的对比结果。图14（a）表明，气液固循环流化床的轴向固含率呈现顶部稀相-底部密相的“S”型分布，轴向流动介尺度模型能准确预测相含率的轴向分布。

在较低的表观液速下，当表观液速不变时，沿轴向增加的方向，固含率逐渐降低，图14（b）、（c）中的气含率与液含率呈现出相反的趋势。这是由于气泡尺寸沿轴向增加的方向不断长大。在较高的表观液速下，体系轴向的较强湍动强化了固体颗粒的流化程度。因此，气含率、固含率以及气泡尺寸均呈现比较均匀的轴向结构，如图14（a）、（c）、（d）所示。

在同一轴向高度上，随着表观液速的增加，图14（c）、（d）显示，气泡先长大后变小，气含率持续降低。在表观液速增大的初始阶段，气液固循环体系的旋涡尺寸较小，不足以导致气泡破裂，仅会将能量传递给气泡，增加气泡之间的接触，促使其发生聚并；而在较高的表观液速下，流动体系中与气泡尺寸相当的旋涡的数量增多，导致气泡破裂；同时，表观液速的增大缩短了气泡在流动体系中的停留时间，导致气含率降低，进一步降低了气泡之间的接触，弱化气泡的聚并行为。在这两个因素的共同作用下，气泡尺寸降低。

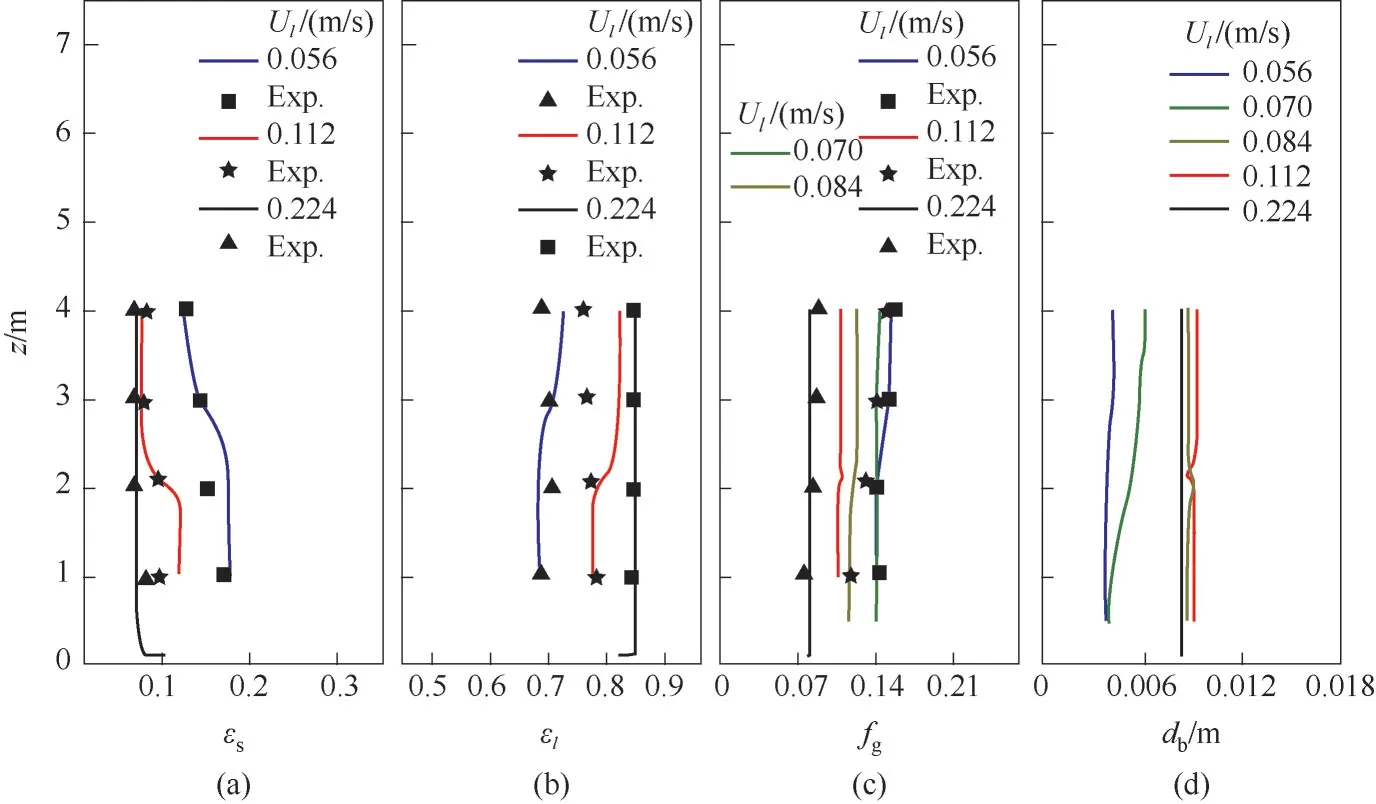
图14 气液固循环流态化体系中的相含率和气泡尺寸轴向分布的模型预测值与实验数据[65]的对比（Ug=0.0488 m/s）Fig.14 Comparison of predicted values of phase holdup and bubble size distribution with experimental data[65]in the gas-liquid-solid circulation fluidization system

2.5 三相流化床径向流动介尺度机理模型

气液固流化床的径向流动介尺度机理建模研究还处于起步阶段[29]。胡宗定等[12]提出的四区模型可以预测气液固流化床的径向流动结构，但是，模型求解需要已知流动体系中相含率的径向分布，并且需要依赖实验求解其中的模型参数。韩社教等[61]将颗粒团的沉降-扩散特性与实验相结合，考察了三相流动的径向参数分布。Lee 等[64]基于气泡的扩散特性，提出了径向气泡扩散模型。这些模型存在的共性问题在于过多引入经验关联式，限制了模型的适用范围，并且未充分考虑流动系统的非均匀结构特征。三相流化床中复杂的多尺度结构是其径向流动特性量化研究的制约因素，EMMS[14]为研究多尺度径向流动行为提供了理论工具，启发Ma等[29]建立了流化低固含率、小尺寸固体颗粒的气液固流化床的径向流动介尺度机理模型。该机理模型指出，气液固流化床中的径向流动结构的主导机制为：固体颗粒总是倾向于聚集在势能较小的位置和床壁面处，流体（包括气泡和液体）总是倾向于通过阻力较小的上升通道；两种主导机制间的竞争和协调关系确定了气液固流化床的径向流动结构。

该模型在求解过程中，通过轴向流动介尺度模型，计算径向流动介尺度模型所需的截面平均参数；将得到的计算结果输入径向流动介尺度模型，预测流化床中的流动参数的径向分布。图15 给出了不同表观气速下，相含率的径向分布的模型预测值与实验值[65]的比较。可以看出，固含率和气含率在流化床边壁处存在较大误差，这与径向流动介尺度模型中引入的经验关联式有关，限制了径向流动介尺度模型的适用范围。该模型主要适用于可将液-固流动相视为拟均相的三相流化床体系，对于大直径固体颗粒、高固含率的流化床的径向流动机理模型，仍需要进行更为深入的研究。

图15 不同表观气速下的相含率的径向分布的模型预测值与实验值[65]的比较（Ul=0.056 m/s，Ud=0.0062 m/s，H=2.02 m，dp=0.0005 m）Fig.15 Comparision of the predictions of radial distribution of phase holdup with the experimental data[65]under different superficial gas velocity

3 结论及展望

气液固流化床内的三相流动行为的机理模型研究已取得较大进展，包括从早期提出的统一尾流模型，到近年来基于能量最小多尺度作用原理而建立的三相流动介尺度机理模型等。基于这些流动机理模型，尤其是新近完善建立的气液固流化床三相流动机理模型，可实现对气液固流化床内三相流动行为的全局参数、轴向及径向流动参数的分布等进行估算。这对工业三相流化床的设计和放大具有重要的指导意义。

但是，由于气液固流体力学理论的发展还很有限，这些机理模型具有一定的局限性。例如，介尺度机理模型将液固混合相视为拟均相。因此，对于小（或轻）固体颗粒的三相流动体系，参数预测比较准确，而对于含大（或重）固体颗粒的三相流体系统，预测有一定误差。原因之一是目前对三相流动系统内复杂的相间相互作用了解有限。例如，对固体颗粒与气泡之间的作用机制，气泡尾流中的气、液、固相之间复杂的相互作用等，还很难通过理论描述加以清楚表达。

随着多相流测试技术的不断进步，可借助于先进的多相流测试技术开展实验研究，考察气泡尾流中旋涡的形成与剥落过程，气泡、液体与固体颗粒间的相互作用机理等。

三相流动系统的非均匀流动结构直接影响相混合、传递和化学反应等过程。所建三相流化床流动介尺度机理模型，能较好地预测多相流动的整体与局部流动结构。在该基础上，进一步探索三相流化床内的相混合、传质和传热特性的定量化规律，并开展具有化学反应的流化床反应特性的研究。

计算流体力学（CFD）模拟过程调用的模型，决定着数值模拟结果与实际状况的接近程度。因此，将所建立的气液固流化床内流动行为的介尺度机理模型与CFD 数值模拟相耦合，开展三相流动态特性等研究，是今后值得考虑的重要方向。