基于状态变换的DVL辅助SINS初始对准方法

王连钊，徐 博，李盛新，李汉领

（哈尔滨工程大学 智能科学与工程学院，哈尔滨 150001）

初始对准即赋予惯性导航系统初始的姿态、速度、位置信息的过程，其对惯性导航系统的导航精度有重要的影响，初始对准技术通常有快速性、精确性的性能要求，随着惯性器件及信息融合算法的发展，这两项指标不断提升，但快速性与精确性的相互约束也越来越明显，通常要根据不同工况进行取舍，在恶劣条件下甚至不能满足任一项[1,2]。SINS初始对准主要包括基于经典控制理论的罗经回路方法、矢量定姿方法及基于最优估计理论的滤波方法。其中罗经回路方法在静态环境下能通过调节阻尼系数方式根据对准精度的需求调整对准时间，能够很好地实现SINS快速初始对准，然而并不适用于较大的机动环境。矢量定姿方法是目前常用的短时间对准方法，因为难以实现器件误差的建模，所以该方法无法突破初始对准的极限精度。现有的初始对准中更多采用“粗对准”+“精对准”两阶段对准的方案[3-5]，其中粗对准通常采用解析计算方法，所需时间短但对准精度较低，主要用来为精对准提供较为准确的姿态初值，令SINS误差模型近似线性[6]；精对准则多采用卡尔曼滤波算法，通过辅助信息完成误差状态的估计。

对于潜航器水下启动，通常仅利用DVL提供辅助信息，由于缺少卫星导航的辅助信息，仅能在较为粗略的初始位置及速度信息基础上结合DVL测量速度信息完成初始对准。在辅助信息不够准确时，机动环境下容易造成矢量定姿方法的粗对准精度不够理想，将直接影响系统误差模型的精度，基于卡尔曼滤波的精对准精度也将下降，导致SINS难以完成快速、高精度动基座对准。现有对粗对准方法研究主要集中在对惯性系对准的优化方案，其缺陷是在动态环境下对外部辅助信息不加判别地利用，将辅助信息误差引入姿态误差中，造成对准精度较低[7]。针对上述问题，文献[8]提出了一种DVL异常值检查和隔离方法，有效地解决了辅助信息不准确对初始对准的影响。文献[9]在优化惯性系基础上改进，提出了基于非线性滤波的精对准方法，在对准过程中可实时更新速度、位置信息。但以上两种方法中未对惯性器件误差建模，降低了对准极限精度。文献[10]针对大初始误差角的初始对准非线性问题提出了一种基于平方根容积信息滤波方法，然而容积滤波器计算量大，不适用于实际工程。文献[11-15]指出在导航坐标系与计算导航坐标系存在较大差异时，传统惯性系误差中速度误差的定义将不能完整描述出当前导航误差状态，若以速度匹配方式进行组合导航，将导致对准效率较低，并总结概括为模型不精确所导致的协方差不一致问题，这点在大初始失准角条件下表现更为突出，同时文献中给出了基于导航坐标系的状态变换的初始对准方法。

本文针对上述系统误差模型不精确所导致的协方差不一致问题给出一种新的解决方案，提出了基于状态变换的SINS初始对准方法。本文推导了基于载体系速度误差方程的SINS系统误差模型；构建了基于状态变换的SINS初始对准滤波模型；最后通过数值仿真及湖面实验验证了所提对准方法的优越性。

1 SINS速度误差问题描述

传统的捷联惯导系统速度误差方程如下：

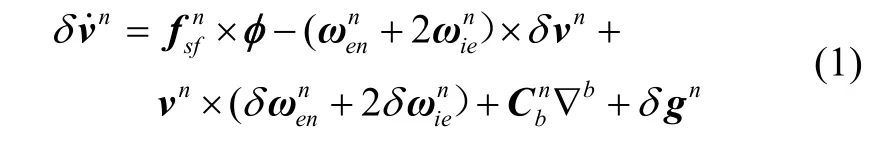
其中速度误差的定义为导航计算机解算速度与真实的导航坐标系速度的差值：

式(2)中速度误差定义仅反映了向量间大小的差异，却忽略了两者坐标系之间的区别，仅在失准角较小时能准确地描述SINS误差状态。若在粗对准未能达到理想的对准精度，后续的精对准将受到较大影响，需要较长的时间完成高精度的对准，不符合初始对准的快速性要求。文献[11-15]中描述为模型定义不准确导致的协方差不一致问题，并针对速度误差定义不严格问题对导航坐标系下速度误差进行了严谨的定义，重新推导了新的速度误差定义下的导航系统速度误差方程，新的速度误差定义如下：

可以看出其中与传统误差模型的主要区别在于速度误差中包含-×φn项，其物理含义为解算速度的角度偏差，主要由失准角引起。

2 基于载体系速度误差的SINS误差方程

式(3)反映了更为严谨的导航坐标系下速度误差，然而在DVL辅助SINS进行导航及对准时，直接获取的是载体坐标系速度信息作为参考，现有方案是利用SINS姿态信息将DVL速度投影至导航坐标系，或将SINS速度信息投影至DVL坐标系，再进行信息融合，这两种方案也引入了部分失准角误差及速度误差，导致了匹配信息不一致问题，误差状态协方差由于模型的不准确的原因不能准确地反映真实的误差状态。为解决以上问题，本文将推导新的基于载体坐标系速度信息的导航误差方程及误差方程，采用惯导解算出载体坐标系速度信息，结合DVL测速信息完成匹配。

将vn=vb代入比力方程，整理比力方程为如下形式：

根据式(4)，SINS计算载体坐标系速度微分方程为：

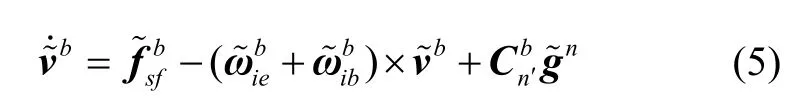
定义载体系速度误差为δvb=-vb，考虑计算坐标系中存在失准角φ、速度误差δ vb、位置误差δ p及重力投影误差δ gn，代入式(5)等号右侧，各项可写为：

将式(4)(5)做差，考虑各误差项为小量并省略二阶以上误差项的乘积，可得载体坐标系的速度误差微分方程为：

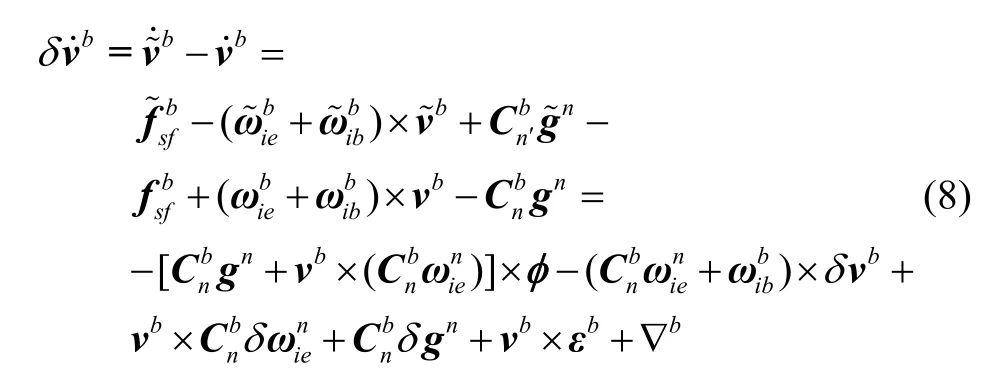
式(8)即是SINS载体系速度误差微分方程，为严谨地完成SINS/DVL组合导航模型，还需要建立载体系速度误差与失准角、定位误差及器件误差之间的关系，本文基于传统的导航坐标系误差方程，建立载体坐标系速度误差与导航坐标系速度误差的关联，再利用传统的导航系误差方程实现较为快速的误差方程建立。

从式(9)可以看出，在传统误差方程中将导航系速度误差替换为δvb的同时，再加入有关失准角的误差项×φ就可以得到基于载体坐标系速度误差的误差方程，将式(9)代入传统姿态误差方程中可得基于载体速度误差的SINS姿态误差方程为：

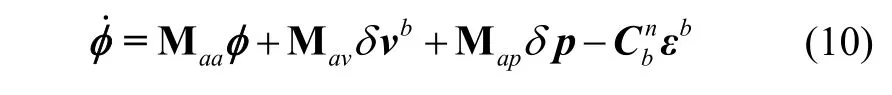
其中，

将式(9)代入传统位置误差方程中，可得基于载体速度误差的SINS位置误差方程为：

其中

短时间内考虑加速度和陀螺仪误差无变化，即为常值偏置加白噪声模型，∇b、εb模型为：

式(8)(10)(11)(12)构成了基于载体速度误差的SINS误差方程，其与导航系速度误差方程的区别是较为明显的。需要指出的是采用式(9)可以快速建立基于载体系速度误差匹配的初始对准量测模型，并实现同样高精度的模型建立，但其仅从量测模型方面进行了改变，并未改变系统模型，这种方案下对准受量测误差影响较大，仍然不能解决误差协方差与状态不一致性的问题，所以由速度微分方程出发建立基于载体系速度误差方程的SINS误差方程是有意义的。同时式(8)也为实现更深层次的SINS/DVL紧组合提供了可能。

3 基于状态变换初始对准的卡尔曼滤波模型

根据已推导出的基于载体坐标系速度的误差方程可建立SINS/DVL组合导航模型，在SINS初始化误差较大时，可由卡尔曼滤波方法实现误差状态的估计，并完成初始对准任务。通常选取SINS误差状态为滤波中的状态变量，在SINS/DVL组合系统中通常存在安装误差角，其对SINS初始对准的影响与载体航行速度相关，不能忽略。

考虑初始对准过程有短时高精度的需求，而SINS和DVL导航系统之间安装的杆臂和DVL量测刻度系数误差已经校正，且短时间内DVL刻度系数误差稳定，安装偏差角较小，则DVL测速模型为：

其中wd为DVL速度测量噪声，安装偏差角ψ将一定程度上影响失准角的估计，因此需将安装偏差角扩充至滤波系统状态中，认为安装偏差角短时间内不变化，其常值模型如下：

选取基于载体系速度误差的SINS误差与SINS/DVL组合导航系统安装偏差角作为初始对准系统待估计状态。卡尔曼滤波器状态量X为：

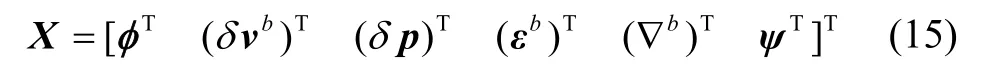
根据式(8)(10)-(12)，连续时间系统模型为：

其中，

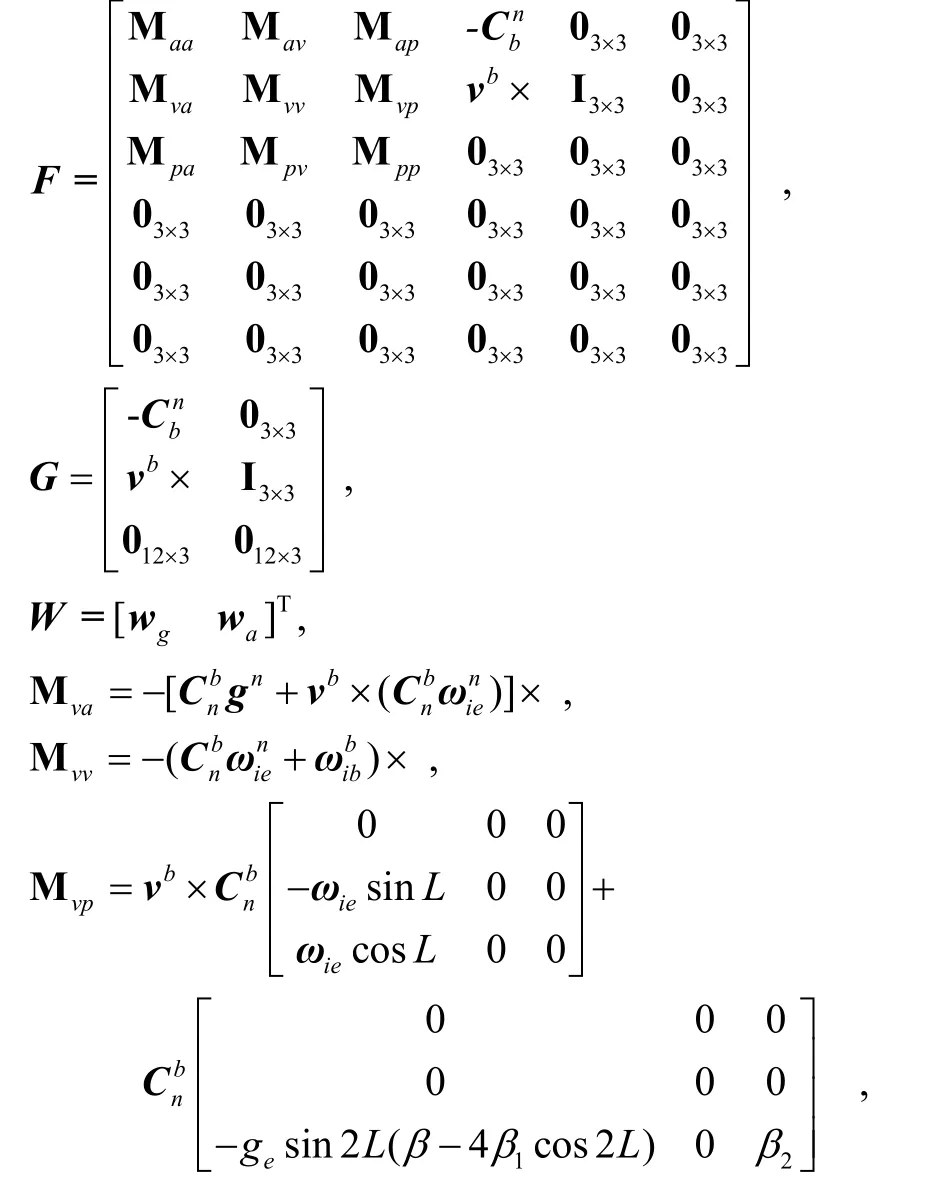
其中wg、wa分别为陀螺仪和加速度计测量噪声。

以T为离散时间对线性微分方程(14)进行离散化，可得离散化的一步转移矩阵Φk/k-1及噪声分配阵Γk-1为：

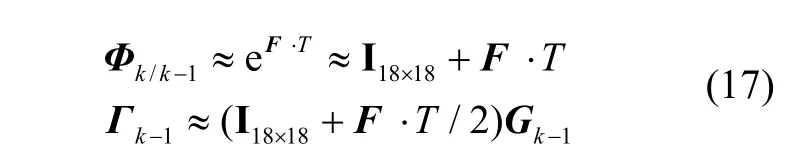
可以看出所建立模型与基于导航坐标系误差方程的传统模型在噪声分配阵部分也存在区别，在速度误差传递方程中不仅有加速度计偏置项，还包含与速度信息耦合的陀螺仪偏置项，这种现象也出现在系统噪声传递中，由此可以看出传统模型中是存在不准确描述的，在滤波中也将导致状态协方差与估计状态一致性差的问题。

4 仿真分析与实验验证

为验证所提出对准方法的有效性，本文进行了数值仿真验证及湖面实验验证。数值仿真部分采用蒙特卡洛仿真说明所提算法的适用性及优势。有限的湖面实验航次用以验证所提出对准算法在实际应用的可行性。为充分反映所提算法的优越性，本文将以下常用对准模型与所提模型进行对比，考虑空间杆臂差异容易被测量并补偿，所以所有验证工作均在杆臂修正基础上展开。为方便说明将所提出的基于载体系速度误差方程的对准模型称为模型1，其余对准模型分别为：

模型3：以传统导航坐标系误差方程为基础，状态量为X=[φT(δvn)T(δp)T(εb)T(∇b)T]T，系统转移矩阵F及观测量同模型2，因为状态中没有考虑安装偏差角的存在，所以量测矩阵H为：

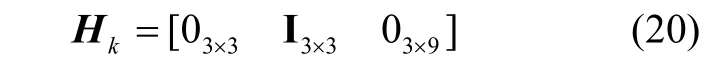
4.1 蒙特卡洛仿真验证

本文主要针对于较大方位初始偏差角及SINS、DVL之间存在安装偏差的环境下，提出一种有效的DVL辅助SINS的初始对准算法，为证明所提算法的一般性，数值仿真部分将在不同条件下进行三组蒙特卡洛仿真。仿真条件为：初始位置误差10 m，初始速度误差0.1 m/s，三轴陀螺常值漂移0.01 °/h，三轴加速度计常值零偏100 μg，DVL测速误差0.1 m/s。三组仿真控制变量如表1所示（±1σ：蒙特卡洛随机变量标准差为1 °）。

表1 三组蒙特卡洛仿真初始误差设置Tab.1 Initial error settings of Monte Carlo simulation

每组实验蒙特卡洛仿真次数为220次，速度为2 m/s，仿真轨迹如图1所示。

图1 蒙特卡洛仿真轨迹Fig.1 Trajectory of Monte Carlo simulation

通常较为关注的方位误差角仿真结果如图2所示，

4.2 湖面实验验证

本文利用湖面实验采集数据对本文提出的基于载体坐标系速度误差方程的对准方法实用性进行验证。船上配备了光纤捷联惯性导航系统（SINS）、法国光纤捷联惯性导航系统（PHINS）、声学多普勒测速仪（DVL）和GPS，其中PHINS与GPS组合系统（PHINS/GPS）作为导航基准用来衡量SINS与DVL的对准精度，主要传感器参数如表2所示。实验分别在船舶岸边系泊状态、湖面直线航行状态和湖面转向机动状态进行对准，各实验状态轨迹特征及DVL测量所得三轴速度如图5所示。实验中未对DVL刻度系数误差进行校正，根据后续实验过程中多次标定所得SINS与DVL之间安装误差角约为[-0.5869,-4.4299,-4.2106] °。

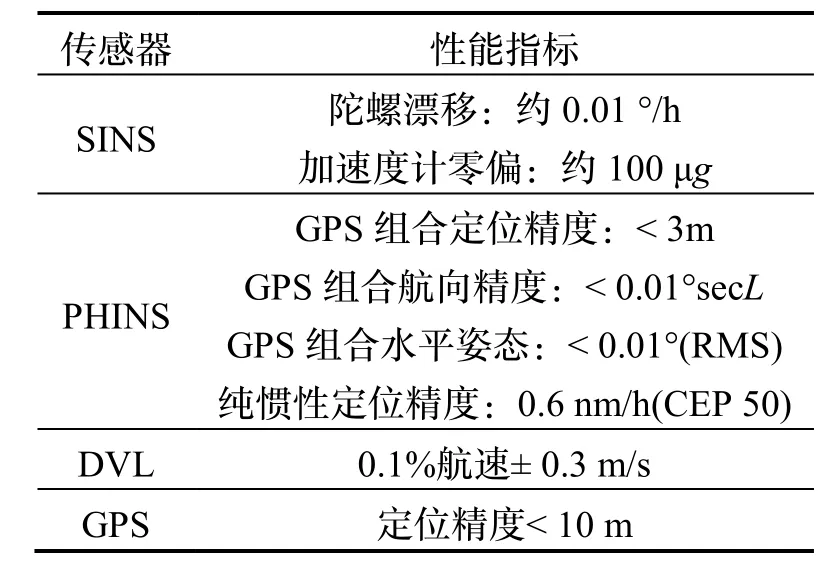
表2 湖面实验主要传感器参数Tab.2 Sensor parameters of lake experiment

图5 实验轨迹及DVL测量速度Fig.5 Experimental track and Measurement velocity of DVL

每组实验仍采用4.1中三种模型进行比较。1200 s对准时间内失准角、速度误差及位置误差估计情况如图6-8所示。由图可以看出在系泊条件下三种模型估计结果几乎一致，速度、位置误差较小，由于PHINS与SINS之间没有做同步触发处理，且两者之间存在安装偏差未进行补偿，所以失准角不为零。在直航条件下，因为存在较大的初始方位误差角，模型2、模型3航向收敛缓慢，且水平姿态误差及速度误差存在较大的变动，位置误差也比较大，而模型1姿态误差、速度误差较为平缓，位置误差也较大，其直接原因是北向速度误差存在恒定的较大误差，误差源为SINS与DVL的安装偏差角未能在直航中有效估计出来。在转弯运动对准实验中三种模型都能有较好的收敛，其中模型1效果最好，航向失准角、速度误差收敛较快，位置误差在转弯后有明显的减小，其主要原因是在转弯后SINS和DVL的安装偏差角一定程度上被估计，位置误差也得到了有效的估计，1200 s时位置误差仅为15.8 m，精度远高于模型2与模型3。

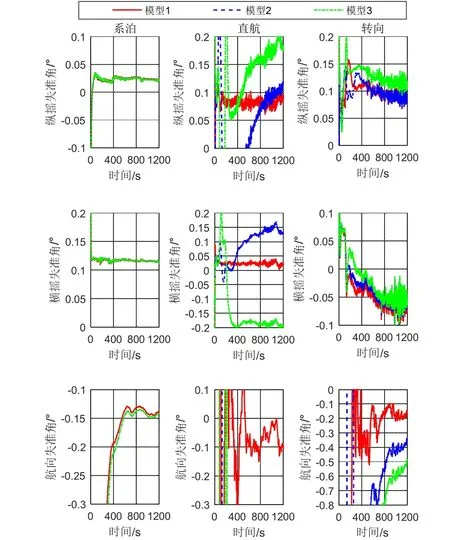
图6 失准角估计结果比较Fig.6 Comparison of misalignment angle estimation results

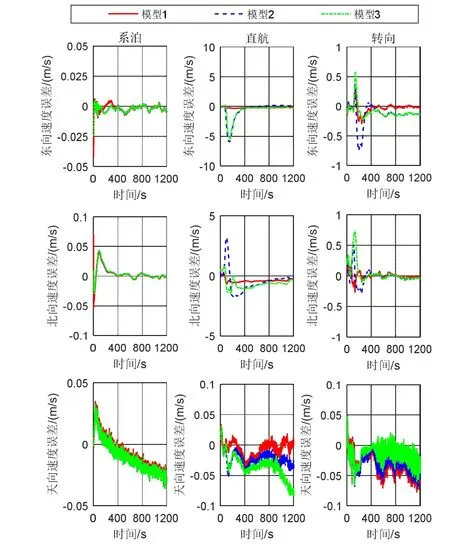
图7 速度误差估计结果比较Fig.7 Comparison of velocity error estimation results

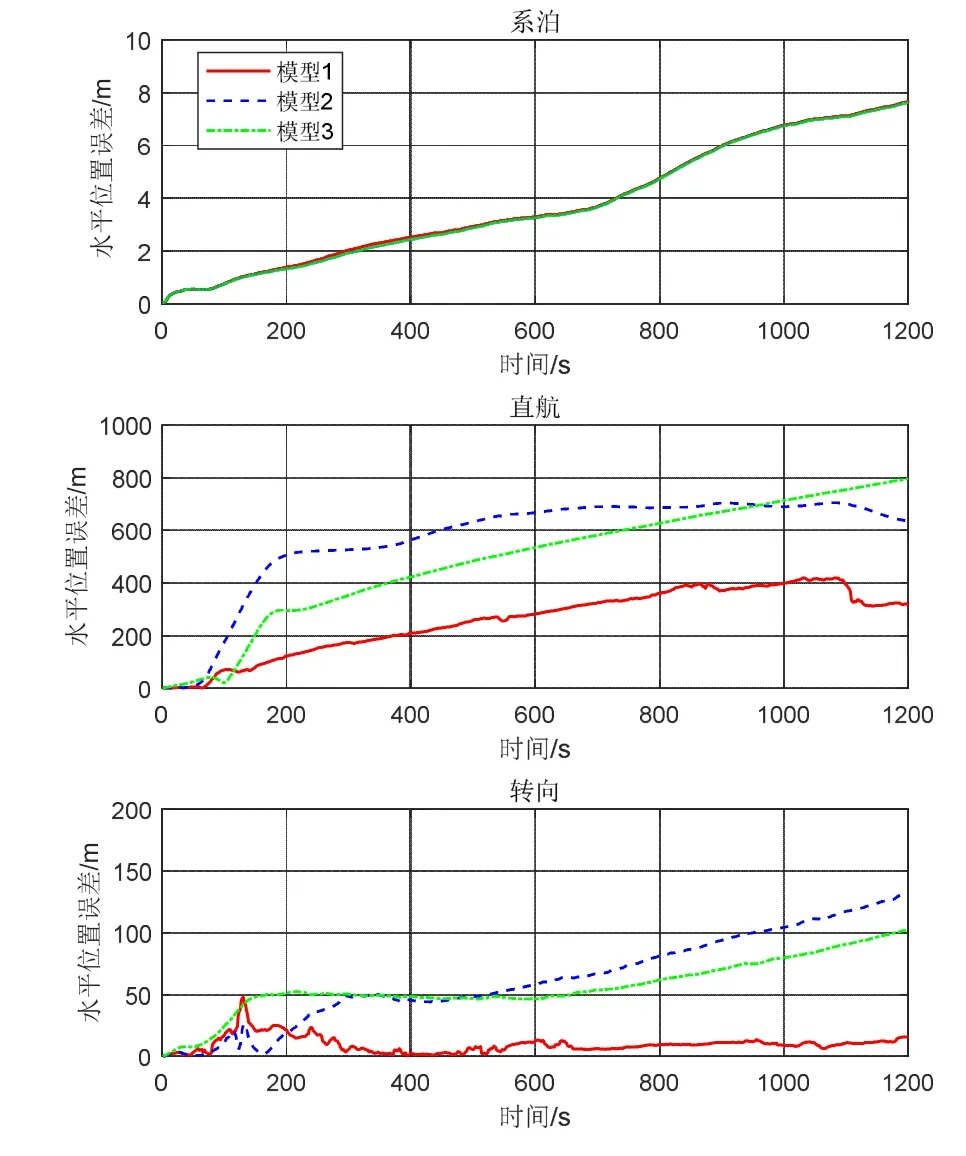
图8 位置误差估计结果比较Fig.8 Comparison of position error estimation results

三种模型对准过程中的器件误差估计情况及SINS和DVL安装误差角估计情况如图9-10所示，模型3未对安装偏差角建模，因此不做讨论。

图9 陀螺漂移估计结果比较Fig.9 Comparison of gyro drift estimation results

图10 加速度计零偏估计结果比较Fig.10 Comparison of zero bias estimation results of accelerometer

系泊和直航条件下可以看出各轴陀螺漂移和加速度计零偏都没有明显的收敛趋势，其主要原因是在系泊及匀速直线运动条件下陀螺等效东向零漂和水平加速度计零偏不可观测。其中由于直线航行时大初始方位误差角造成量测误差较大也造成了模型2、模型3陀螺漂移、加速度计零偏过估计情况。在转弯对准实验中，陀螺漂移和加速度计零偏有明显收敛趋势，其中陀螺漂移收敛与实验室测试环境下所得结果接近，而加速度计零偏超出100 μg，其原因为实验船只较小，在实验过程中线运动较为明显，加速度计动态误差较大，这也是造成动态对准姿态结果与系泊对准姿态存在明显区别的主要原因。

5 结 论

本文以大初始方位误差角为背景，针对传统DVL辅助SINS模型不精确造成的初始对准精度低、时间长的问题，提出了基于载体速度误差方程的初始对准模型。由比力方程出发，建立新的初始对准模型，并由蒙特卡洛仿真实验及湖面实验验证了所提出初始对准模型的有效性。蒙特卡洛仿真实验在多种误差源环境下证明所提模型在常规使用环境中精度与传统模型精度相差不多，在大方位误差角及SINS和DVL间存在明显安装误差角条件下能大幅度提高对准精度及定位精度。湖面实验结果证明所提模型在大初始方位误差角结合多运动状态条件下能实现高精度初始对准，且在存在转弯机动的环境下能获得高精度位置估计。综合以上，可以证明本文所提出的基于载体系速度误差方程的初始对准模型能有效提高对准模型精度，在大方位误差角条件下所提对准方法相对于传统对准方法有明显优势。