基于UKF与互补滤波的随钻IMU井斜动态测量方法

杨 海，冯选璋，单代伟，刘骕骐，张立早，罗 顺

（1. 石油天然气装备教育部重点实验室（西南石油大学），成都 610500；2. 西南石油大学 机电工程学院，成都 610500；3. 四川宏华石油设备有限公司，成都 610036；4. 中国石油集团 西部钻探工程技术研究院，乌鲁木齐 830000）

1 井斜测量原理及其影响因素

1.1 井斜测量原理

1.2 动态井斜测量的影响因素

式中Ac为钻进过程中钻柱高速旋转所产生的离心力加速度信号，Ay是钻具振动所产生的振动加速度信号，As高强度的瞬时冲击信号，Ag是重力加速度。

（2）对陀螺仪的影响因素：

在钻进过程中钻头位置的陀螺仪角速度测量信号Bdynamic可表示为：

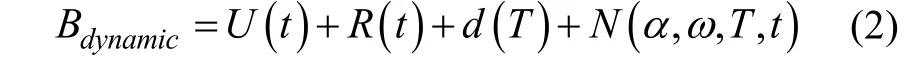
式中U（t）为真实角速度信号；R（t）为随机噪声；d（T）为温度漂移；N（α,ω,T,t）为加速度、角速度、温度、时间等因素所造成的总影响。

2 干扰信号的滤除

在随钻动态测量中，针对加速度计冲击干扰信号幅值大、变化剧烈、时间跨度短的特点，使用限幅滤波对随机产生的脉冲干扰进行滤除，限幅后后续信号数据输出到其他滤波器中[13]；针对陀螺仪的高频精度随机游走噪声和量化噪声，对陀螺仪进行一阶数字低通滤波。

2.1 基于UKF的有色噪声滤除

动态测量过程中由于近钻头处恶劣振动环境以及传感器本身测量精度问题将会导致三轴加速度计和陀螺仪测量数据中包含大量有色噪声。针对传感器的有色噪声，采用能够连续递推运算的无迹卡尔曼滤波算法滤除[14]。

基于加速度计和陀螺仪的测量结果，建立非线性态数学模型，若t时刻的模型状态方程为（t）为：

式中n（t）为系统状态噪声，A（t）为状态转移矩阵,Q（t）为前一时刻的状态方程。

观测方程为：

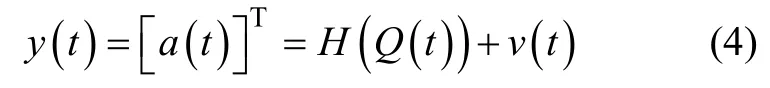
式中H函数为非线性函数，y（t）为t时刻的传感器测量向量，v（t）为t时刻限幅滤波后的测量噪声。分别对状态方程和观测方程进行离散化处理后，选取sigma点为：

式中n为状态方程中状态变量个数，计算权值后，计算时间的更新方程，通过状态方程将sigma点进行非线性传播。

结合方差矩阵Pk-1得到下一步预测协方差矩阵：

计算观测更新方程：

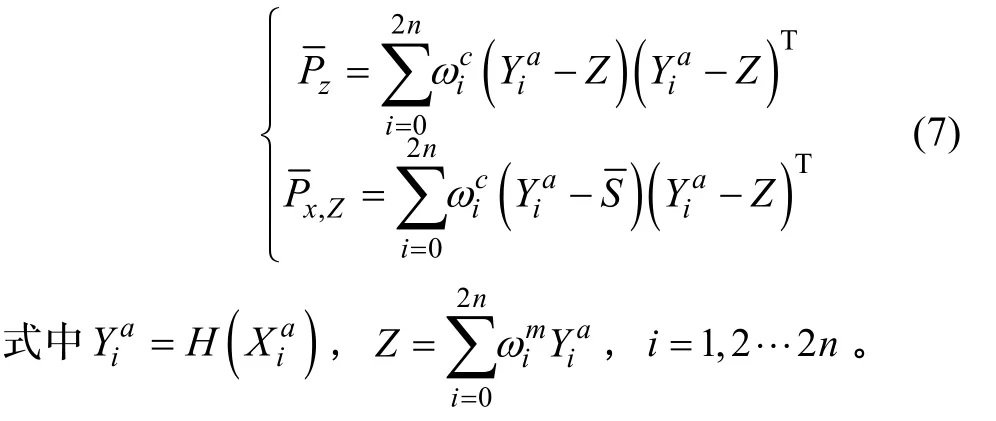
滤波更新得到：

2.2 基于互补滤波算法的陀螺仪零偏噪声滤除

陀螺仪受振动影响较小，但是由于零偏不稳定性和温度漂移等原因导致零偏误差严重，即使校正后也不能完全消除。并且由于陀螺仪角度信息是由角速度积分得到，而经积分作用，长时间误差会积累，所以陀螺仪主要需要解决的是低频零点噪声。在经过前述对加速度传感器和陀螺仪的一系列滤波后，本文使用加速度计获得的角度信息去矫正陀螺仪获得的姿态信息，从而使算出来的陀螺仪零偏角度误差减小[15]。其步骤如下：

（1）对过滤后的加速度信息进行归一化

由于姿态变化矩阵中的四元数是规范四元数，利用陀螺仪更新的四元数也要进行归一化，所以加速度计获得的值也需归一化才能将两者对应。

（2）获取陀螺仪算出的姿态矩阵中的重力分量

加速度传感器是在物体坐标系下测得的值，所以也应提取利用角速度算出的姿态矩阵中的物体坐标系下的重力分量，记为Vx、Vy、Vz。

（3）将加速度传感器获得的重力向量归一化后的值与提取的姿态矩阵的重力向量叉乘获取姿态误差ex、e y、ez。

（4）对姿态误差进行积分，得到误差角速度值。

3 信号提取及井斜测量算法仿真验证

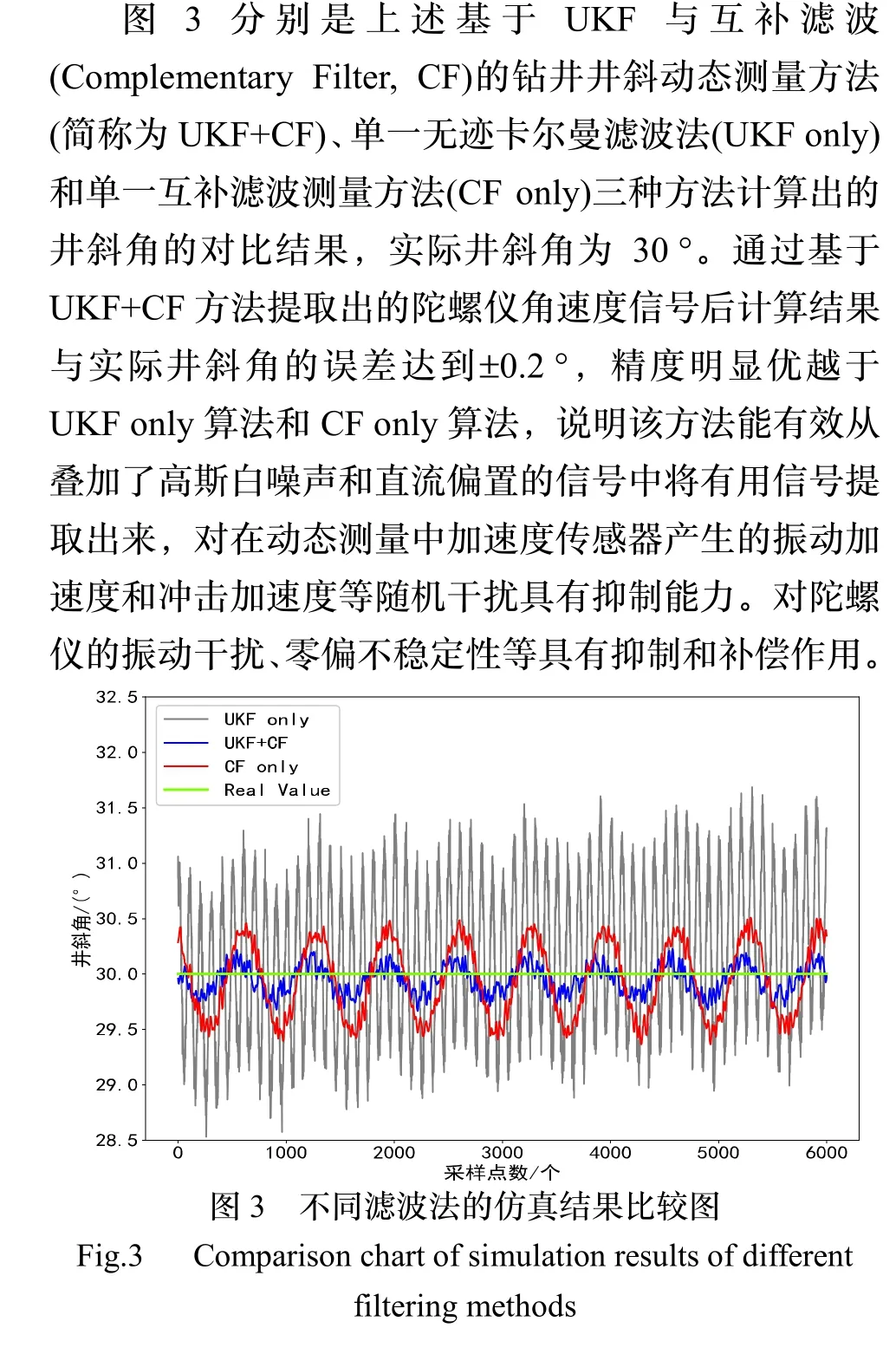
4 实验测试及分析

4.1 实验平台的搭建

4.2 实验结果及分析

由图11所示，在不同井斜角和不同转速的测量条件下，本文方法都能对井斜角进行准确测量。井斜角测量精度优于± 0.2 °，最大误差为+ 0.19 °，说明该方法适用于不同转速下的连续井斜角测量。

图11 井斜角计算误差Fig.11 Deviation angle calculation error

最后，将本文方法与其他滤波方法进行对比，利用各方法对旋转振动测试系统进行测试，这些方法包括低通滤波（Low Pass Filter, LPF）、低通滤波和UKF的复合滤波(LPF+UKF)、互补滤波(CF)和UKF+CF。旋转振动测试系统的参数设置和转速与上述一致。不同转速下倾角的最终测量结果如表2所示。

表2 在差异转速下使用不同方法求得的计算结果Tab.2 Calculation results obtained using different methods at different speeds

由表中的测量精度和最大误差可知，LPF、LPF+UKF和CF方法计算倾角误差较大，即便使用LPF+UKF方法，测量精度也只能达到± 0.4 °。此外，三种方法的测量精度还受转速的影响，测量误差随着转速的增加而增大。而本文采用的UKF+CF方法不仅将测量精度提高到± 0.2 °，而且整体测量精度不受钻具转速的影响。

4.3 现场钻井数据检验与分析

为了验证算法的有效性，利用现场钻井近钻头随钻测量仪器在井下工作过程中存储并经过地面导出的实测数据对算法进行性能检验。将所提出基于UKF与互补滤波的钻井井斜动态测量方法（UKF+CF）与仅互补滤波方法（CF only）进行对比测试。测试数据来源于辽宁省某井实际2226井钻井过程的一段，该段数据来自2301～2302 m的深度，钻井速度为222～236 r/min。停钻后，静测井倾角为29.96 °～30.08 °。以该深度位置的现场数据作为测试数据，因为其倾角与上述测试环境基本一致，便于比较。以X轴和Y轴的提取结果为例，钻进过程角速度原始测量结果如图12-13所示，与上述实验测试相比，现场数据中含有大量冲击干扰信号，但滤波后的数据更加平滑，有效提取了X轴和Y轴的角速度信号。最后，利用从不同方向的陀螺仪提取的角速度信号来计算井斜角。测试井2301 m～2302 m井斜角计算结果如图14所示，红线为仅采用互补滤波器（CF only）处理的计算结果，蓝线为UKF+CF处理的计算结果，实际该位置的井倾角为29.96 °∼30.08 °。从图14中可以明显看出，采用CF only法提取重力加速度结果计算的井斜角精度低于采用UKF+CF法计算的井斜角精度。同样，使用现场数据的测试结果与上述实验结果基本一致，UKF+CF法测井倾角精度达到± 0.2 °，远高于CF only法的± 0.5 °。

图12 X轴角速度原始测量结果Fig.12 Original measurement result of X-axis angular velocity

图13 Y轴角速度原始测量结果Fig.13 Original measurement result of Y-axis angular velocity

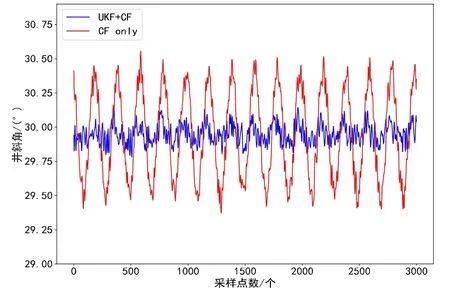
图14 井斜角计算对比图Fig.14 Comparison chart of well deviation calculation

5 结 论

针对动态井斜测量环境中，陀螺仪和加速度计易受钻具振动、温度等影响，导致提取信号误差较大，进而导致井斜测量不准确的问题，本文提出了一种利用无迹卡尔曼滤波与互补滤波的井斜动态测量方法。通过模拟动态过程中近钻头位置的陀螺仪和加速度计的干扰噪声和工况环境对本方法进行仿真测试，再通过基于旋转振动测试系统实验平台对不同转速下角速度的提取效果进行实验验证。最终实验测试结果与仿真测试结果一致，计算的井斜角精度优于± 0.2 °，工具面角变化连续平滑。同时在钻具转速为60～300 r/min内，0 °～90 °的井斜角测量最大误差为+0.19 °，并且测量结果稳定性不受钻具转速影响。最后利用现场数据进行检验，结果表明井斜角精度达到± 0.2 °。结果证明该方法能抑制陀螺和加速度计输出的干扰噪声和消除零偏误差，有效地提取出不同方向的角速度分量，提取出的不同方向的动态重力加速度分量所计算的井斜角，达到现场测量要求标准，相比较于使用低通复合滤波法和无迹卡尔曼滤波器检测的角速度提取法± 0.5 °的动态测量精度，具有更高的角度测量精度，同时测量精度并不受钻具转速限制。