融合评分相对差异的协同过滤推荐算法
王丽萍,傅 攀,邱飞岳,陈 宏
1(浙江工业大学 计算机科学与技术学院,杭州 310023) 2(浙江工业大学 教育科学与技术学院,杭州 310023)
1 引 言
随着计算机技术的发展,推荐系统被应用在越来越多的领域[1],包括物品与资源推荐、学习资源推荐[2]以及医疗健康领域中的患者康复训练方案推荐[3]及患者表现预测[4]等.推荐系统正逐步影响着我们的生活,目前推荐算法大致可以分为基于协同过滤的推荐、基于内容的推荐、基于知识的推荐等类型[5-8].基于协同过滤的推荐算法的核心思想之一是通过寻找目标用户的相似用户,将他们感兴趣的内容推荐给目标用户.基于内容的推荐算法通过提取物品特征与用户偏好特征并通过相似度计算为用户推荐相关项目.而基于知识的推荐算法则是根据特定领域的知识为用户推荐相关内容.
基于协同过滤的推荐算法是最经典的同时也是目前最流行的推荐算法之一[5,8].基于协同过滤的推荐算法包括基于内存的协同过滤和基于模型的协同过滤.基于内存的协同过滤又可以分为基于用户的协同过滤和基于物品的协同过滤,两者的核心都是通过相似度计算完成推荐,区别在于前者计算用户相似度,后者计算物品相似度.基于模型的协同过滤通过对用户和项目的关系建立关联模型,通过模型求解项目的评分预测实现推荐,常用的方法有矩阵分解和贝叶斯方法等.
虽然基于协同过滤的推荐算法在诸多方面呈现出巨大优势,如方法易于实现、不需要太多的领域知识,但是在不同的场景下依然面临许多问题,如冷启动、数据稀疏问题[5,7]等,这些都会影响推荐质量.为了改善推荐质量,众多研究从不同角度出发,充分挖掘潜在信息,使协同过滤推荐算法可以应用于更加广阔的场景.文献[9]将用户社会信任信息整合到非负矩阵分解(NMF)的框架中,缓解了数据稀疏和冷启动问题.文献[10]提出一种自适应矩阵分解方法,自适应地改变最小化函数,获取了更高的预测准确率.文献[11]考虑时间因素,将用户评分形成评分序列,计算序列相似度.文献[12]认为用户对物品的评分受情境影响,考虑用户评分时的时间、地点等信息.文献[13]引入了项目的标签并计算用户-标签相似度,文献[14]引入了用户的人口统计属性(年龄、性别、职业等)进行相似度计算,并证明了引入的额外信息有助于提升推荐质量.文献[15]认为可以利用间接邻居信息来提高推荐质量.除此之外,针对相似度计算的问题,文献[16]基于KL散度提出一种非对称的相似度计算方法,能有效提高稀疏数据集上的推荐精度.文献[17]提出一种基于α散度的项目相似度计算方法,降低了对共同评分项的依赖.文献[18]提出局部相似度的概念,认为用户对某些特定主题的物品更加感兴趣.文献[19]提出了一个基于L-P范数的相似度计算方式,可以有效改善推荐质量.文献[8]提出一种新的相似度计算方法,将相似度计算公式应该满足的条件转化为数学方程,通过数学方法求解出相似度计算的表达式,最终证明基于新的相似度计算公式的推荐算法优于许多其他具有代表性的方法.文献[6]指出将带有结构信息的相似度与评分相似度进行混合可以减少算法对邻居数的依赖.
本文基于余弦相似度,提出一种融合评分相对差异的用户间相似度计算方法,考虑评分之间的相对差异并引入放大系数,更加有效地区分了用户间差异,在非偏好评分场景中可以降低算法的预测误差,与其他同类方法相比有一定竞争力.
2 相关工作
2.1 基于用户的协同过滤算法
传统的基于用户的协同过滤算法主要涉及的对象有:用户U,项目I,以及用户对项目的历史评分Rui.其主要步骤包括[5,17,20]:1)利用用户对项目的历史评分构造用户-项目评分矩阵,对于未知评分通常标记为0;2)利用用户-项目评分矩阵计算用户间相似度;3)根据用户间相似度选出与目标用户最相似的K个用户作为邻居集合;4)根据邻居用户的评分信息预测目标用户对未知项目的评分;5)将预测得分最高的N个项目推荐给目标用户.

表1 用户-项目评分矩阵Table 1 User-item scoring matrix
如表 1所示,用户-评分矩阵的行索引代表用户集合用U表示,U={U1,U2,…,Um},列索引代表项目集合用I表示,I={I1,I2,…,In},Rmn代表用户Um对项目In的评分.值得注意的是,用户-项目评分未知时评分记为0,当项目数量较多时,该矩阵将会是一个较为稀疏的矩阵.
用户间相似度的计算主要依赖用户评分向量,两个用户的评分向量之间的相似度将作为用户相似度.如何准确计算用户间相似度是基于用户的协同过滤推荐算法的关键步骤.
2.2 用户相似度计算方法
常见的相似度计算方法主要有余弦相似度(COS,Cosine)[6-8]、皮尔逊相关系数(PCC,Pearson correlation coefficient)[6-8]、修正余弦相似度(ACOS,Adjusted cosine)[6-8,21],计算公式为:
(1)
(2)
(3)
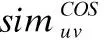
PCC和ACOS考虑了用户个人的评分习惯[7],有的用户可能偏向给高分,而有的用户偏向给低分.如式(2)、式(3)所示,PCC和ACOS会在原始评分的基础上减去用户评分均值后计算用户间相似度.当用户的评分由用户主观偏好给出时,这样的处理方式可以起到改善推荐质量的作用.但是在一些非用户偏好评分场景中,用户-项目评分由特定的标准衡量得出时,例如学习项目表现评分、训练项目表现评分等,PCC和ACOS难以准确衡量用户间差异.
文献[22]中指出余弦相似度不能准确反映两个用户向量之间的相似度.如图 1(a)所示,考虑向量间余弦相似度,向量A与向量B之间的相似度等于向量A与向量C之间的相似度.向量B与向量C的余弦相似度为1,无法体现出差异.

图1 相似度示例Fig.1 Example of similarity
相似度计算方式还有杰卡德相似系数(Jaccard)[6-8]、均方差(MSD,Mean squared difference)[6-8],杰卡德相似系数只考虑用户间共同评分项的数目,并没有考虑用户的具体评分.均方差考虑的是用户共同评分项分值上的差异,非常依赖共同评分项.具体计算公式为:
(4)
(5)
其中Iu和Iv分别表示用户u和用户v各自评过分的项目集合.
当以上两种相似度结合后可以得到新的相似度计算方法杰卡德均方差(JMSD)[6,23],计算公式为:
(6)

3 融合评分相对差异的协同过滤推荐算法
3.1 融合评分相对差异的相似度计算
皮尔逊相关系数和修正余弦相似度在非偏好评分的场景下不能准确衡量用户间相似度,余弦相似度不能衡量评分规模上的差异,基于评分差值的相似度又仅考虑共同评分项之间的差异,存在无法准确衡量多个用户间差异的情况.为了更加准确地计算非用户偏好评分场景下用户间相似度的计算,降低评分预测误差,以提高基于用户的协同过滤算法的推荐质量,使其能更好地应用在更多场景中.本文基于余弦相似度并利用用户评分分值相对差异提出一种改进的用户间相似度计算方式.
由于余弦相似度没有考虑具体评分规模上的差异,所以改进的相似度需要计算用户评分间数值上的差异.又因为用户存在未评分项目,所以无法通过用户对所有项目的评分计算用户间评分差异,只能利用用户共同评分项目.
利用用户共同评分可以计算出评分之间的平均绝对差异,但是平均绝对差异容易受某个较大差异影响导致不能准确衡量用户评分间的整体差异,例如现有评分向量A=(1,1,4),B=(1,1,1),C=(2,3,1),A、B之间的平均绝对差异,B、C之间的平均绝对差异都为1.但是整体上看A和B有两项相同评分,A和B之间的总体差异可能更小.所以平均绝对差异并不适合直接用于修正余弦相似度,本文利用共同评分之间的评分相对差异进行余弦相似度修正.现给出相关定义与计算公式如下:

(7)
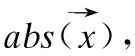
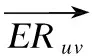
评分相对差异用于衡量用户共同评分项之间的评分相对差异,表示为:
(8)

为了使用户间差异满足对称性[18],对式(8)进行调整,将评分绝对差异除以两个目标用户共同评分项的对应评分之和.
(9)
以用户评分和作为除数,会使差异变得不明显.在式(9)的基础上进一步处理,以用户评分均值作为除数.一方面满足对称性,另一方面克服以用户评分和作为除数导致差异不明显的问题.最终评分相对差异计算公式为:
(10)
定义3.归一化累计差异Duv
归一化累计差异用于衡量用户间差异.为了使用户间差异可以进行横向对比,将评分相对差异向量的各位进行累加得到累计差异,并作归一化处理:
(11)
(12)

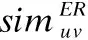
评分相对相似度,将用户间差异转换为相似度,计算公式为:
(13)
评分相对相似度,依赖共同评分项,并不适合单独作为用户间相似度计算方式.而且当用户间没有共同评分项时,通过该方式计算会得到用户间差异为0,相似度为1,并不正确.
通常相似度的结合或修正手段有加权、相乘、特殊函数映射等[6,8,14].加权的方式通常难以得到准确的权重系数,需要进行大量的实验,特别是当数据规模存在较大差异时,如何确定准确的权重系数将会是一件困难的事.通过特殊的函数映射来对数据修正,通常需要特定的领域知识或基础理论,否则难以找到适合的映射函数.
本文提出的评分相对相似度适合采用相乘的方式与余弦相似度结合,以达到修正的目的.首先,余弦相似度在数据维度较高时具体值会比较小,而评分相对相似度相对偏大,如果采用加权的方式进行修正,确定合适的权重系数以保证修正效果将非常困难.其次,当用户间没有共同评分项时,余弦相似度为0,评分相对相似度为1,如果采用加权的方式进行修正会导致明显错误.而采用相乘的方式可以保证该极限情况下的兼容性,即两个相似度相乘后结果仍为0.所以本文提出的评分相对相似度以相乘的形式对余弦相似度进行修正是最佳选择.

(14)
通过结合评分相对相似度,可以克服余弦相似度无法准确衡量评分规模上的差异的缺点.
表2给出的用户评分示例为4个用户在两个项目上的评分,其中用户U4无项目I2评分.表 3、表 4、表 5分别为针对表 2的余弦相似度、评分相对相似度以及改进的用户相似度.

表2 用户-项目评分示例Table 2 Example of user-item scoring
通过U1,U2间的相似度和U1,U3间的相似度可以看出,改进的相似度可以克服余弦相似度无法衡量规模上的差异的问

表3 用户余弦相似度Table 3 COS similarity of users
题.如果仅考虑共同评分项,U1,U4间的相似度和U2,U4间的相似度将会相同,但是假设U4对I2的评分已知为1,那么

表4 用户评分相对相似度Table 4 ER similarity of users
U4和U1,U2间的相似度不同.从示例的相似度计算结果中可用看出,改进后的相似度计算方法能更加有效地区分相似度.

表5 改进的用户相似度Table 5 COS-ER similarity of users
3.2 放大系数α
本文中的放大系数指在使用评分相对相似度对余弦相似度进行修正时加入幂运算,对应幂运算的指数即为放大系数.文献[6]中指出幂运算可以扩大数据差异,调整数据规模.为使最终的相似度计算更加有效,本文使用放大系数对评分相对相似度进行调整.
所以,本文提出的改进的用户间相似度计算方法最终计算公式为:
(15)
其中α为放大系数.
相对余弦相似度而言,由于评分相对相似度只基于共同评分项计算,偏差较小.通过放大系数α,可以扩大相似度之间的差异.另外放大系数可以降低数据中的噪声,使得小值被忽略[24].放大系数α的缺点是其最佳取值需要通过具体实验进行对比分析后得出,而且幂运算增加了计算量.
4 实验结果与分析
4.1 数据集
本文在两组数据集上对算法有效性进行实验验证,分别是MovieLens100K数据集和开放大学学习分析数据集(OULAD,Open University Learning Analytics dataset)[25].
MovieLens100K数据集包含943名用户对1682部电影的评分记录,共计100000条.该数据集中的用户评分基于偏好,评分区间为1-5分,每个用户至少为20部电影评过分,数据密度约为6.3%.
OULAD中包含了开放大学学生的学习表现数据,其中包含学生各次学习任务表现评分,得分区间为1-100.该数据集中的评分是一种非偏好评分.本文实验取其中3000名学生学习数据,包括105次学习任务,保证每名学生至少有5次评分结果,共计23058条评分记录,数据密度约7.3%.
本文采用Python作为编程语言,基于LensKit[26]工具包进行实验.实验数据按80%训练集,20%测试集进行交叉验证.
4.2 评价指标
推荐算法的主要目的是预测用户在某些项目上的喜好或表现.存在大量评价指标,两个常用的指标包括平均绝对误差(MAE,Mean Absolute Error)[7,17]和均方根误差(RMSE,Root Mean Squared Error)[7,17],公式定义如下:
(16)
(17)
其中T代表测试集中的用户评分集合,Rui代表用户真实评分,pui代表预测评分.
4.3 参数设定
本文提出的改进的相似度计算公式存在可变参数α,α的具体值会影响相似度计算.取邻居个数K=10,20,30,40,50,60,70分别在两个数据集上进行实验,所提方法在不同α取值下MAE和RMSE结果如图 2所示.
由图2(a)、图2(b)可以看出,在MovieLens100K数据集上,MAE、RMSE值随着α从1递增到7时整体呈下降趋势,当α递增到5之后,MAE与RMSE都出现了个别上升的情况.为保证整体效果,在MovieLens100K数据集上进行的实验中α设置为6.
由图 2(c)、图 2(d)可以看出,在OULAD数据集上,MAE随着α从1递增到7时整体呈下降趋势,在递增到6后趋于稳定.RMSE在α递增到4之后下降缓慢,而且在6递增到7出现上升的情况.所以本次在OULAD数据集上进行的实验中α同样也设置为6.
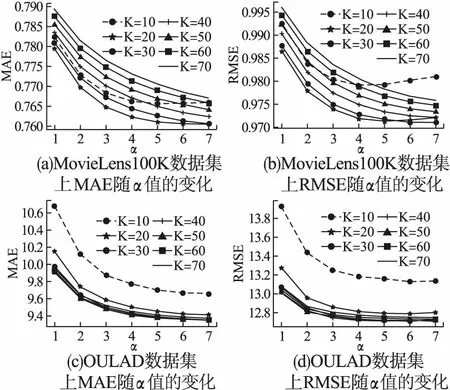
图2 MAE和RMSE随值的变化Fig.2 MAE and RMSE changes with α value
4.4 结果与分析
本文提出的相似度计算方法记为COS-ER,将其与COS、MSD、Jaccard、JMSD、OS[8]、ACOS、PCC等相似度计算方法进行对比实验,邻居数K取10,20,30,40,50,60,70.其中OS被证明是一种较好的相似度计算方法[8].
另外本次实验还对比了另一种合并的相似度计算方法记为COS-MSD,由余弦相似度和均方差合并而来,主要用于验证基于绝对误差的MSD方法无法直接用于修正余弦相似度,COS-MSD方法计算公式如下:
(18)
各方法在MovieLens100K数据集上预测误差指标如图 3、图 4所示,在OULAD数据集上的误差指标如图 5、图 6所示,分别包含了各方法在不同邻居个数K下的MAE和RMSE结果.

图3 MovieLens100K数据集上不同算法MAE值对比Fig.3 Comparison of MAE values of different algorithms corresponding to MovieLens100K
如图 3所示,在MovieLens100K数据集上,针对平均绝对误差MAE,本文提出的相似度计算方法COS-ER较COS方法有一定改善,MAE下降比例约为5%,较Jaccard方法MAE下降比例约为5.5%,较MSD方法MAE下降比例约为2.5%,较OS方法MAE下降比例约为1.6%,较JMSD方法表现相似.直接由COS方法和MSD方法合并而来的COS-MSD方法表现较差,可见MSD方法无法用于修正余弦相似度.
如图 4所示,在MovieLens100K数据集上,针对RMSE指标,本文提出的COS-ER方法明显优于JMSD,RMSE下降比例约为2.5%,说明COS-ER方法较JMSD方法更稳定.同样的,COS-ER方法也略优于OS方法,RMSE下降比例约为1.4%.

图4 MovieLens100K数据集上不同算法RMSE值对比Fig.4 Comparison of RMSE values of different algorithms corresponding to MovieLens100K
综上所述,COS-ER方法在余弦相似度的基础上额外考虑了评分规模上的差异,降低了预测误差,但是由于没有考虑用户的评分偏好,所以在基于用户偏好评分的MovieLens100K数据集上表现不及PCC和ACOS.
如图 5所示,在OULAD数据集上,针对平均绝对误差MAE,本文提出的相似度计算方法COS-ER较COS有较大改善,MAE下降比例约为24%,较MSD方法MAE下降比例约为28%,较Jaccard及JMSD方法MAE下降比例约为18%,较ACOS方法MAE下降比例约为7%,较PCC方法MAE下降比例约为4.7%,较OS方法表现相似.

图5 OULAD数据集上不同算法MAE值对比Fig.5 Comparison of MAE values of different algorithms corresponding to OULAD
如图 6所示,在OULAD数据集上,RMSE指标所反映的结果和MAE指标基本相同.但本文提出的方法COS-ER在RMSE指标上略优于OS方法,RMSE下降比例约1.2%.

图6 OULAD数据集上不同算法RMSE值对比Fig.6 Comparison of RMSE values of different algorithms corresponding to OULAD
Jaccard、MSD、JMSD这3种方法极度依赖共同评分项,当用户间共同评分数量较少时难以准确计算用户间相似度,导致无法发现邻居用户,预测质量较差.与ACOS和PCC相比,在OULAD数据集上COS-ER方法表现较好.由于OULAD数据集中用户-项目评分为非偏好评分,ACOS和PCC并不能准确计算用户间相似度.COS-MSD方法的结果再次表明,直接将考虑绝对误差的MSD方法和COS方法结合,并不能修正COS方法.
由上述实验结果对比分析可知本文提出的COS-ER方法通过评分相对相似度对余弦相似度进行修正是有效可行的.由于基于余弦相似度并且考虑了评分规模上的差异,COS-ER方法可以更加准确地区分用户间相似度.在偏好评分的场景下较部分传统方法效果更好,并且在非偏好评分的场景下,可以在一定程度上降低预测误差,提高推荐质量.
5 总 结
本文基于余弦相似度提出一种融合评分相对差异的协同过滤推荐算法,更加适用于非偏好评分场景,利用评分间相对差异以及放大系数对余弦相似度进行修正,可以更好地计算用户间相似度.通过在两组不同类型的数据集上进行对比实验,结果表明本文提出的方法在偏好评分的场景下,效果优于多数方法,在非偏好评分场景下,效果优于所有对比方法,可以降低预测误差,提高推荐质量.

