基于粒子群算法的地磁矢量测量系统一体化校正
王振雄,张 琦,潘孟春,陈 卓,王 泽,任鑫田
(国防科技大学智能科学学院,湖南 长沙 410073)
0 引 言
地磁场是地球的固有属性,传统的地磁场测量通常为地磁总量,称为TMI测量。但是地磁场是一个矢量场,相对于地磁总量,地磁矢量含有更为丰富的信息[1],在地磁导航[2-3]、磁目标探测、矿产勘探以及地质分析中具有良好的应用前景。捷联式地磁矢量测量系统具有可搭载于不同的载体上,系统小型化,成本低等优点。但是捷联式矢量测量系统中三轴磁传感器本身存在误差;惯导和三轴磁传感器由于安装位置较近,存在干扰;惯导和磁传感器的坐标系由于不可视,存在非对准的问题。以上种种因素制约了捷联式地磁矢量测量的精度。但是目前对捷联式地磁矢量测量系统的校正通常是对上述的三种误差独立进行研究,王一[4]以合成磁场总量的误差最小为目标函数求取校正参数,但是未考虑惯导干扰以及惯导和磁传感器坐标系的非对准误差;Ali等人[5]提出基于最小二乘和神经网络的三轴磁传感器校正法,但是该方法需要外部的辅助向量;高全明[6]采用平面旋转校正法对磁传感器和惯导之间的非对准误差进行校正,需要系统严格绕两轴转动,实用性不强;Pang等人[7]提出基于正六面体的安装误差校正方法,实现了惯导和磁传感器的坐标系对准,但是校正后无法脱离辅助的正六面体,可操作性不强;李婷[8]提出了一种改进的模糊自适应的卡尔曼滤波方法来对矢量测量中的干扰进行补偿,有效的提高了矢量误差补偿的精度。
通过分析以上误差的模型的特点,以地磁总量为约束,建立地磁矢量测量系统的一体化校正补偿模型,并采用粒子群算法对参数进行求解,有效提高了捷联式矢量测量的准确度。
1 校正原理
1.1 三轴磁传感器误差模型
目前三轴磁通门传感器的误差主要来源于三轴非正交、刻度因子不同以及零偏误差[9]。假设三轴的非正交角分别为 α,β,γ,其坐标系和理想坐标系的关系如图1所示。

图1 三轴传感器坐标系和理想坐标系
假定三轴磁通门传感器的坐标系原点和理想坐标系的原点重合,传感器坐标系的z轴和理想坐标系的w轴重合;三轴传感器的x轴位于理想坐标系的uOz平面内,与u轴的夹角为 α;三轴传感器y轴与理想坐标系uOv面的夹角为γ,其投影和理想坐标系的v轴夹角为β。另外,由于磁通门传感器三轴的性能也不完全相同,导致三轴的零偏误差和刻度因子也不完全相同,假设零偏为B0=[B0xB0yB0z]T,三轴的刻度因子分别为kx,ky,kz。三轴磁通门传感器的误差模型为:

B=[B1B2B3]T——理想坐标系下的真实磁场。
1.2 干扰磁场模型
对于捷联式矢量测量系统,需要将惯导和三轴磁传感器刚性固定,一般情况下,惯导与三轴磁传感器的距离较近,因此惯导中的铁磁性器件也会对三轴磁通门传感器的测量产生干扰。其中干扰磁场主要分为软磁干扰和硬磁干扰[10]。磁场干扰模型为

式中:Bi——三轴磁传感器的测量值;
M——感应系数矩阵;
B——传感器坐标系下地磁场;
MB——感应磁场,即软磁干扰;
Bp——剩余磁场,即硬磁干扰。
因此,三轴传感器的实测值则为

1.3 综合误差模型
通过上两节的误差模型可知,综合影响下传感器的测量值为
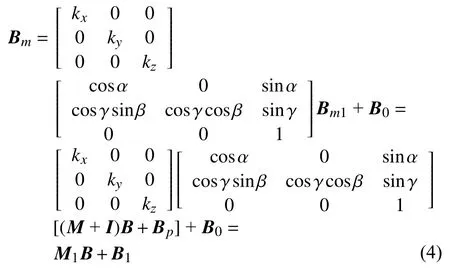
B会随着传感器的姿态变化而改变,设惯导的航向角为α0,俯仰角为β0,横滚角为γ0,则地理坐标系到惯导坐标系的旋转矩阵[11]为:


因此捷联式地磁矢量测量系统的综合误差模型为:

式中:Mt——上述两类误差合成的总的感应系数;
Bd——两类误差合成的总的偏置误差。
2 基于粒子群算法的参数求解
对式(7)进行变换,得



此外,地磁场的三分量合成的总量值还需要满足实测地磁总量的约束,则有XTHX=Bt2,,Bt为地磁场总量。至此,问题转化为对带有约束的线性方程组的求解。粒子群算法(PSO)是一种有效的全局优化算法,它是基于群体智能理论的优化算法,通过群体中的粒子间的合作与竞争产生的群体智能指导优化搜索[12],对于解决当前多维参数的求解具有很大的优势。
采用粒子群优化算法对式(9)的参数求解的步骤如下:
1)构造适应度函数。对于式(9)的求解,参考距离平方和最小,构造以下适应度函数:

当适应度函数F(X)越小时,表示经参数求解越接近真实值,因此目标函数为minF(X)。
2)初始化粒子群,为避免群体规模太小陷入局部最优,同时考虑算法的复杂程度,设置群体规模为n=200;粒子X的维度15;设置粒子范围,粒子的速度范围以及惯性权重w,最大迭代次数tmax,学习因子c1,c2等参数,并对粒子的位置和速度在范围内进行初始化。
3)判断粒子是否满足总量约束,若满足约束,根据式(10)计算每个粒子的适应度函数;若不满足约束,则将其适应度函数设置为无穷大。
4)根据下式选择粒子个体最优值pbest和全局最优值gbest,其中,pbest表示个体取得最优适应度Pbest对应的位置;gbest表示取得全局最优适应度Gbest对应的位置。

5)位置和速度更新。对于满足总量约束的粒子,按下式更新粒子的速度和位置:

对于不满足总量约束的粒子,下次更新跟随种群的速度方向,即按下式更新粒子的速度和位置:
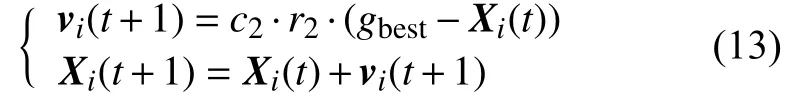
式中:t——当前迭代次数;
r1和r2——[0,1]之间的均匀随机数。
6)判断迭代结束条件:若t≥tmax,迭代结束,返回最优解gbest,其中包含所求解的参数;否则返回步骤3)继续执行。
7)根据求得的Mt-1和Bd对传感器测量得到的数据进行校正并转到地理坐标系下,得到地理坐标系下的地磁矢量。
3 仿真及实验验证
为验证基于PSO算法的地磁矢量测量误差校正的有效性,分别进行了仿真验证和实验验证。
3.1 仿真实验验证
参考WMM世界地磁模型中长沙地区的地磁场参数,设置地磁矢量Be=[34 889-2 383 34 011]T,人为设置式(7)中的感应系数矩阵和偏置误差如下:

设置传感器的不同姿态,得到的传感器的测量值如图2所示。可以看到,三轴传感器的输出随着姿态的变化而变化,并且由于误差的影响,三轴数据合成的磁场总量也存在波动。

图2 传感器各轴仿真输出及合成总量
采用本文中提到的PSO算法对传感器的测量数据进行校正参数求解,并根据校正参数进行校正,得到的校正参数的估计值与设置值基本一致,校正后的数据如图3所示,校正后得到的地磁矢量都与设置值相同,证实了本文算法的可行性。


图3 校正前后仿真数据对比
为了检验所提出算法的抗噪声能力,分别对三轴磁传感器的测量数据添加5 nT和10 nT的随机误差,经过PSO算法校正后合成总量和x,y,z轴的标准差分别为 4.68 nT、4.95 nT、4.70 nT、4.76 nT和 5.22 nT、12.69 nT、13.41 nT、13.22 nT。添加噪声后的仿真结果表明本文提出的方法具有一定的抗噪声干扰能力。
3.2 实验验证
为进一步验证本文所提的矢量测量校正方法,选择长沙郊区的磁环境稳定的地点进行实验。实验中使用的三轴磁传感器非正交误差小于0.1°,线性误差为0.001 5%;惯导姿态误差小于0.01°。
将三轴磁传感器和惯导通过铝制无磁平板刚性地固定在一起,构成捷联式地磁矢量测量系统,如图4所示。实验过程中,首先使用质子磁力仪测量得到地磁总量为48 845.53 nT,作为总量约束。然后在同一地点人为转动磁传感器和惯导构成的地磁矢量测量系统,对不同的姿态下的磁数据和姿态进行采集,采集到的磁数据如图5所示。

图4 捷联式矢量测量系统

图5 Mag-13传感器输出数据
采用本文中提到的校正方法进行校正,校正前后的数据如图6所示,校正前合成总量和x,y,z轴的标准差分别为 166.42 nT、11 867.77 nT、11 707.69 nT、12 422.90 nT;校正后分别降为 11.92 nT、17.51 nT、19.41 nT、7.9 nT。实验结果表明具有本文所提方法具有一定的校正效果和实用性。

图6 实测数据校正前后对比图
4 结束语
针对捷联式地磁矢量测量系统的误差特点,建立了地磁矢量测量系统的误差一体化校正模型。采用粒子群算法对捷联式地磁矢量测量的误差参数进行估计,并对该算法进行了仿真和实验验证。仿真结果表明,求解得到的参数与设置的参数基本一致。对三轴磁通门传感器和XW-GI惯导构成的地磁矢量测量系统进行实验验证,校正前合成总量和x,y,z轴的标准差分别为166.42 nT、11 867.77 nT、11 707.69 nT、12 422.90 nT;校正后分别降为 11.92 nT、17.51 nT、19.41 nT、7.9 nT,有效的提高了测量准确度。仿真和实验结果表明本文提出的校正方法对于地磁矢量测量系统具有较好的校正效果,具有一定的实用性。

