水下爆炸载荷下复合点阵夹层结构冲击响应分析

毛柳伟，祝心明，黄治新，李营*

1 海军研究院，北京 100161

2 武汉理工大学 理学院，武汉 430063

3 北京理工大学 先进结构技术研究院，北京 100081

0 引 言

水下爆炸是舰船主要毁伤载荷之一，严重威胁了舰船生命力。水下爆炸可分为装药爆轰、冲击波传播和气泡脉动3 个重要阶段[1-3]。文献[4]详细叙述了不同阶段下水下爆炸的物理与化学现象及其变化，分析了水下爆炸载荷的分布与传播特点，建立了水下爆炸冲击波载荷的经典半经验半理论公式。该理论沿用至今，已得到不断的发展与完善。在水下爆炸的现象和冲击波载荷特性方面，大量的学者开展了相关研究。Geers[5]提出了双重渐进近似方法（DAA），这是一种预先求解流固耦合载荷的方法，又称解耦方法，在水下爆炸应用中得到了不断的发展与完善。李国华等[6]通过测量水下爆炸载荷作用下浮动冲击平台的动态响应，得到了相应的冲击谱，经分析发现，冲击谱上的3 个阶段分别对应于水下爆炸产生的冲击波、气泡运动诱发的滞后流以及气泡脉动压力。辛春亮等[2]比较了不同数值模拟软件在水下爆炸载荷作用下其各方面的性能，发现在远场爆炸计算方面，ABAQUS 软件具有更大的优势，计算速度快且稳定性好。张阿漫等[1]从实船实验、理论分析和数值方法3 个方面对水下爆炸当前的研究状况进行了总结分析，并概括了水下爆炸载荷的特性及其对舰船的毁伤特性。

为提高舰船生命力，近年来，学者们针对爆炸和冲击载荷下典型防护结构的能量吸收性能开展了大量研究，主要对象包括蜂窝结构、泡沫结构和点阵结构等[7-16]。经研究发现，蜂窝和泡沫结构具有较高的能量吸收效率，不过其结构的可设计性较小，抗冲击性能难以进一步提高。金属多孔点阵结构具有高度的可设计性和三维周期性，以及较低的表观密度和较高的孔隙度，能够有效吸收冲击载荷的能量。随着增材制造（AM）技术的迅速发展，点阵结构在船舶、航天、汽车等领域均得到了广泛应用。Ostos 等[7]将点阵结构的压缩应力−应变曲线分为了3 个阶段，即线弹性阶段、平台阶段和密实化阶段。Elsayyed 等[17]提出了8 位组桁架（octet-truss）点阵结构。Ushijima 等[18]针对体心立方晶格（body-centered cubic，BCC） 胞元单胞的力学性能进行了理论计算，发现减小单胞的宽高比，增加支柱的直径，可以提高单胞的初始刚度和塑性破坏强度。

除多孔材料以外，纤维增强复合材料（fiber reinforced plastic，FRP）由于其高比刚度和比强度特性，被广泛应用于抗冲击领域[19]。由于在冲击载荷下纤维的脆性被破坏，导致其能量吸收效率相对较低。而FRP 和金属多孔点阵结构的结合因能兼顾金属的延展性和复合材料的高比强度特性，因而能获得更佳的抗冲击性能。但是，有关复合材料−点阵夹芯结构在水下爆炸载荷下的毁伤和能量耗散机制仍不清楚。

本文将考虑将碳纤维增强复合材料（carbon fiber reinforced plastic，CFRP）面板和点阵铝夹芯结构组成新的复合材料−点阵夹芯板结构，研究其在水下爆炸冲击波载荷下的抗爆抗冲击性能，同时，将动态响应量化为与夹芯板几何参数间的函数设计关系，寻找最优的结构设计参数并使能量吸收最大化，用以为非接触水下爆炸冲击波载荷下复合夹层板结构的冲击响应研究提供参考。首先，通过有限元软件ABAQUS 对不同结构参数下CFRP−点阵铝夹芯板在非接触水下爆炸冲击波载荷作用下的动态响应进行数值模拟，然后，在此基础上对CFRP−点阵铝夹芯板结构的能量吸收及变形进行优化设计，提升结构的防护性能。

1 材料与方法

1.1 响应面法及理论

水下爆炸冲击波载荷下夹芯板结构的抗冲击问题具有几何大变形和高度非线性的特点，传统的优化方法局限性很大，故一般采用代理方法进行求解。代理优化方法实质上是一种近似替代的方法，包括响应面法、Kriging 法、径向基神经网络法和人工神经网络法等，这些方法是通过拟合或插值建立代理优化模型，用已知点的响应信息来估计未知点的响应信息。其中，响应面法是解决相关问题最有效的替代方法之一，是解决多变量问题和系统可靠性分析的常用方法，被广泛应用于结构耐撞性、管材液压成形、激光切割、焊接工艺等各种工程领域[20-21]。

响应面法（response surface methodology，RSM），即响应曲面设计方法，是一组有助于深入了解和优化响应的实验设计（design of experiment，DOE）技术。如果确信或者怀疑某些因素对目标存在非线性影响，就可以建立包含这些主要因素的一次项和平方项的数学函数，预测目标响应值与这些因素之间的关系，用较短的试验周期和较少的试验次数精确、高效地得到多学科设计优化问题的最佳试验条件。有关响应面优化，首先选择合适的基函数形式，建立设计变量和结果输出的待定关系，然后利用实验设计方法在设计域内取样，对所取样本点进行数值分析，并用最小二乘法对基函数进行拟合，最后构造近似代理优化问题并予以求解[21]。

响应近似函数可以假定为一组基函数的和：

基函数可以有多种选取形式，常用的有一次和二次完全多项式：

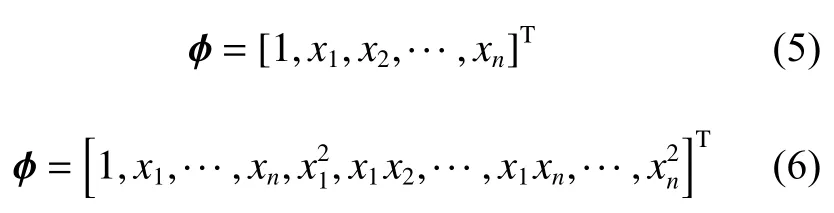
样本点的选取可以利用正交设计方法。一次线性回归的正交设计可以采用正交设计表进行，二次回归的正交设计通常采用中心复合设计（central composite design，CCD）[21-22]进行，图1 所示为该方法的一种形式，其中涉及到三次以上的问题比较少见。

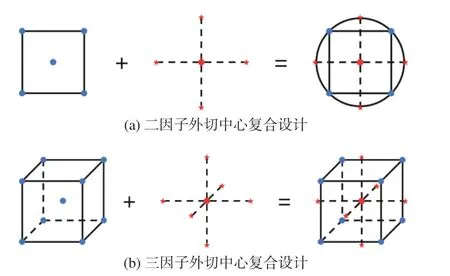
图1 外切中心复合设计Fig. 1 Central composite circumscribed design

拉丁超立方抽样（Latin hypercube sampling，LHS）这种实验设计方法由McKay 等[23]于1979 年提出。该方法采取在空间中均匀分布样本点的形式，可以看作是在n维 向量空间中抽出m个样本。其基本过程是将n维向量空间的每一维平均分成长度相等的m个区间，从每一维不同区间内随机抽取一个样本点，然后将这些随机抽取的样本点形成一个样本，总共可以得到m个样本。这是一种非常高效的方法，能够确保覆盖到所有变量范围，如图2 所示。

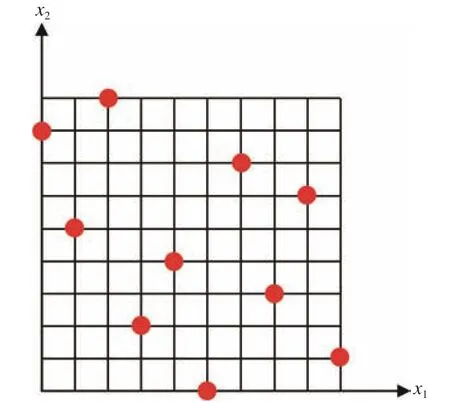
图2 随机拉丁超立方抽样Fig. 2 Random Latin hypercube sampling

1.2 有限元模型的建立

为了探究非药式非接触水下爆炸冲击波压力载荷作用下CFRP−点阵铝夹芯板的动态响应，使用有限元软件ABAQUS 建立计算模型，利用ABAQUS/Explicit 进行显式动态分析，进行了三维有限元模拟。

整个有限元模型由2 个CFRP 板及其夹芯层，以及加载水舱组成。其中，加载水舱长600 mm；飞片直径80 mm，厚10 mm；活塞直径80 mm，厚20 mm，活塞深入激波管内部并与管口平齐，且飞片与活塞间隔1 mm；CFRP 板上、下面板直径均为140 mm，厚度均为1 mm，每个面板有4 层纤维层，每层厚0.25 mm，CFRP 板受到水下冲击波载荷作用时的有效面积区域直径为80 mm；夹芯层为1 层，厚5 mm，中间采用的是一种基于八支架单元结构（Octet）的铝质点阵结构，由16×16 个胞元排列组成，每个胞元可以看作是立方体外部6 个面的12 条对角线和内部连接相邻面心的12 条线构成的杆件组成，长、宽、高均为5 mm，杆件直径为1 mm，单胞结构如图3（a）所示。夹芯板结构如图3（b）所示，数值仿真模型如图3（c）所示。图中，飞片、活塞、加载水舱和CFRP−点阵铝夹芯板均采用拉格朗日方式建模，水域采用欧拉方式建模。

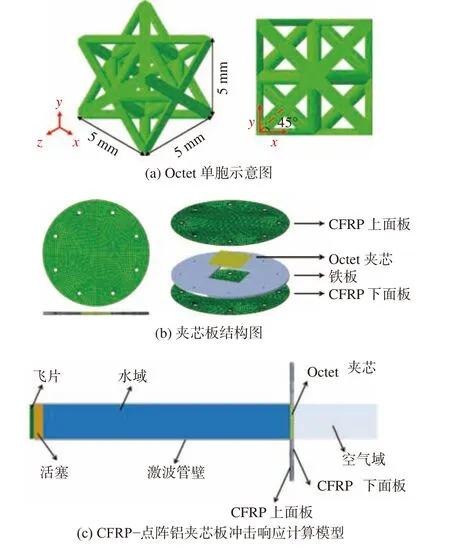
图3 CFRP−点阵铝夹芯板的有限元模型Fig. 3 Finite element model of CFRP - lattice aluminum sandwich plate

1.3 材料本构模型

CFRP 板的上、下面板均为碳纤维增强复合材料，该材料由多层碳纤维布通过环氧树脂浸润硬化而形成。本文选用的碳纤维布采用的是双向编织工艺，即纤维沿着平面2 个垂直方向经纬双向分布，并以一定的工艺编织而成，其纤维方向平面内应力−应变关系为正交线弹性。CFRP板的力学参数如表1 所示。

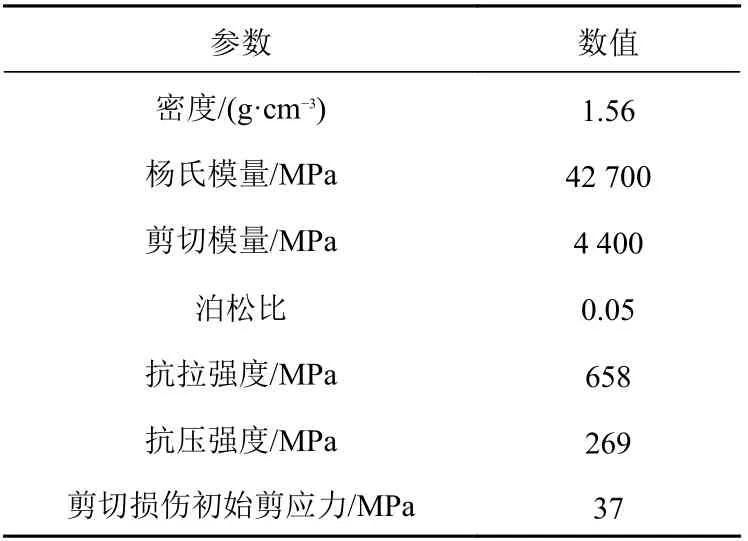
表1 CFRP 板部分材料参数（单层）Table 1 Partial material parameters of CFRP (lamina)

夹芯层Octet 点阵结构采用的是铝合金材料，其部分材料参数如表2 及图4 所示。

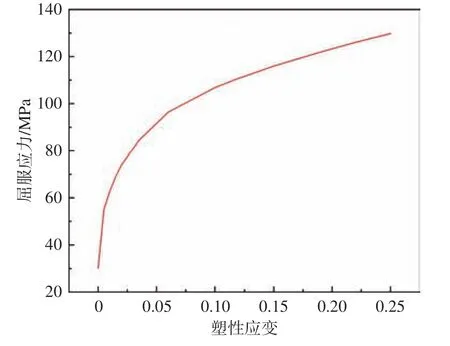
图4 铝合金屈服应力−塑性应变曲线Fig. 4 Yield stress-plastic strain curve of aluminum alloy

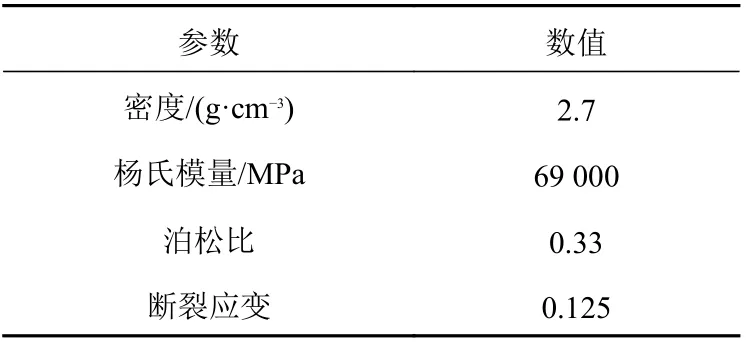
表2 铝合金部分材料参数Table 2 Partial material parameters of aluminum alloy

激波管中的流体介质为水，使用线性Us−UpHugoniot 状态方程模拟不可压缩流体有黏和无黏的层状流动，具体形式为：

水的具体参数如表3 所示。

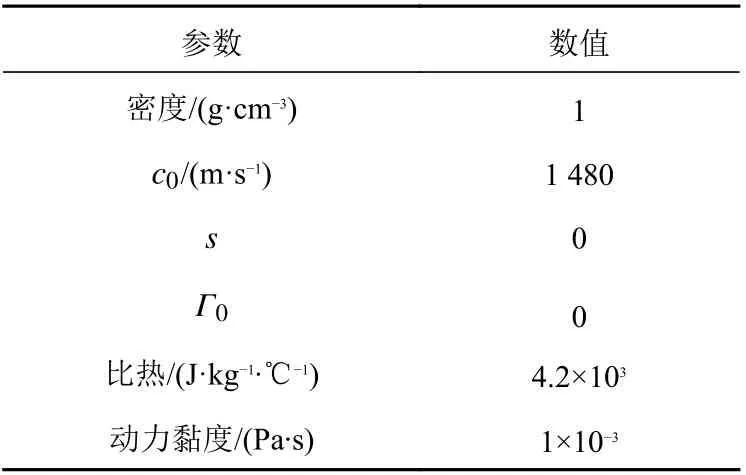
表3 水的材料参数Table 3 Material parameters of water

1.4 载荷、边界条件及网格划分

Deshpande 等[24]针对一维波动理论进行了理论推导，认为对于较远处流场的峰值压力，可以通过改变飞片的初始运动速度来进行调节，冲击波的衰减速率则可以通过改变飞片和活塞的质量进行调节。可以表示为：

式中：p0为冲击波峰值压力；cw， ρw分别为水声速度和水的密度；v0为飞片的初速度；mp为飞片质量； θ为衰变时间。考虑到冲击波的充分反射，作用在静止板上的冲量I0可以计算为：

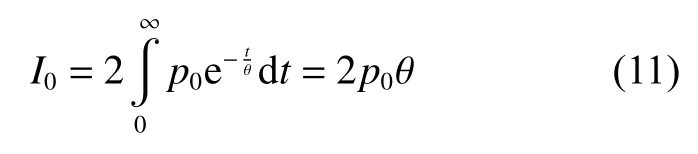
根据非药式水下爆炸冲击波加载系统的实验原理，设置系统的初始条件为飞片的撞击速度，设置速度为10 m/s（近似远场水下爆炸，作用于结构上的冲击波峰值约为15 MPa）；对激波管外表面采用固定约束，并由8 个螺栓固定CFRP−点阵铝夹芯板。设置模型的总计算时间为3 ms，此时CFRP 板的下面板已经回弹，可以满足计算要求。网格划分需要考虑计算的精度和效率，若划分的网格尺寸较大，会影响软件计算的精度，造成计算出的CFRP 板下面板的位移（变形）和模型总能量不能满足要求；若划分的网格尺寸太小，软件计算的效率会大大降低。因此，有必要选择合理的网格尺寸。在分析讨论网格尺寸之前，需要对数值仿真的有效性进行验证。

2 结果与讨论

2.1 模型验证

通过ABAQUS 软件建立5A06 铝合金固体板在空背加载条件下的计算模型，如图5 所示。首先，利用一种非接触水下爆炸模拟装置[25-26]对铝板施加冲击波载荷，然后，分析加载水舱加载位置处压力传感器测得的冲击波峰值，并且与Huang 等[27]的试验结果进行了对比。整个有限元模型由1 个铝板及其夹芯层，以及加载水舱组成，其中加载水舱长500 mm，压力传感器距加载水舱管口20 mm；飞片直径66 mm，质量0.13 kg；活塞直径66 mm，质量0.22 kg，活塞深入激波管内部并与管口平齐，且飞片与活塞间隔 1 mm；铝板直径160 mm，厚0.5 mm，铝板受到水下冲击波载荷作用的有效面积区域直径为66 mm。图中，飞片、活塞、加载水舱和铝板均采用拉格朗日方式建模，水域采用欧拉方式建模。其中，铝板在水下冲击波载荷作用下垂直于面板平面方向的位移如图6 所示（图中，U为铝板位移，U3为垂直于面板铝板平面方向的位移分量）。图7 给出了管口处冲击波压力峰值。由图可知，采用数值模拟方法与实验所得的压力峰值相差10.5%，验证了数值方法的有效性，同时可认为，在一定范围下，不同欧拉域网格尺寸对板的动态效应影响不大。因此，为提高计算效率，选择欧拉域网格尺寸为5 mm。

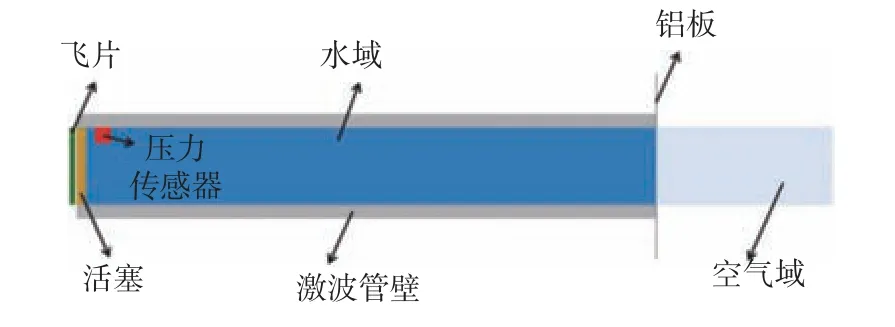
图5 铝板冲击响应计算模型Fig. 5 Calculation model of impact response of aluminum plate

图6 铝板在水下冲击波载荷作用下变形过程剖面图Fig. 6 Profile of deformation process of aluminum plate under underwater shock wave load

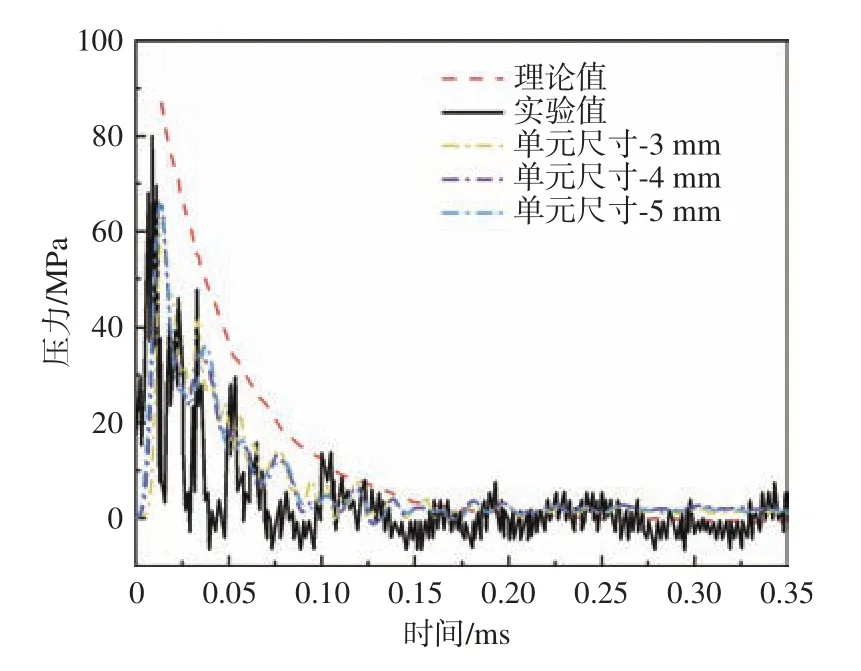
图7 管口处冲击波压力峰值Fig. 7 Peak value of shock wave pressure at the tube opening

2.2 冲击波载荷作用下CFRP−点阵铝夹芯板的动态响应

由上节的讨论，考虑将CFRP−点阵铝夹芯板计算模型中的欧拉域网格尺寸设置为5 mm，CFRP 板的网格尺寸设置为4 mm。利用ABAQUS软件对CFR−点阵铝夹芯板在非药式非接触水下爆炸冲击波作用下的动态响应进行有限元仿真分析，其模型尺寸参数如表4 所示。

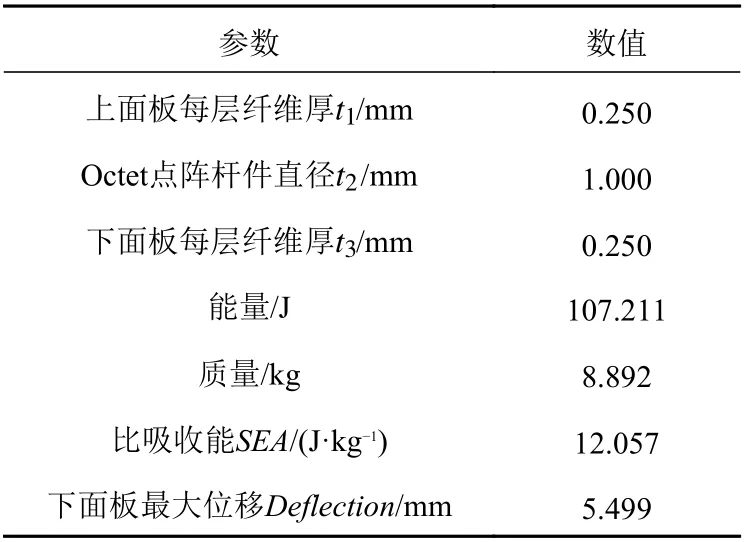
表4 CFRP−点阵铝夹芯板模型尺寸参数Table 4 Model parameters of CFRP−lattice aluminum sandwich plate

通过计算，发现下面板在1.77 ms 时位移达到最大值，随后出现回弹，位移开始减小。在该时刻，上、下面板及夹芯的Mises 应力云图以及下面板的位移云图如图8（图中，S为Mises 应力，U4为下面板的位移）所示。从图中可以看出，CFRP 的上、下面板及夹芯材料并没有发生破坏，最大变形发生在CFRP 下面板中心处。对于夹芯板的抗爆性能，采用以下参数作为评估能量吸收效果的指标：下面板最大位移Deflection和比吸收能SEA。结构吸收的总能量用E表示，m为夹芯板的总质量。将通过比吸收能SEA来衡量单位质量结构的能量吸收性能，可以表示为：

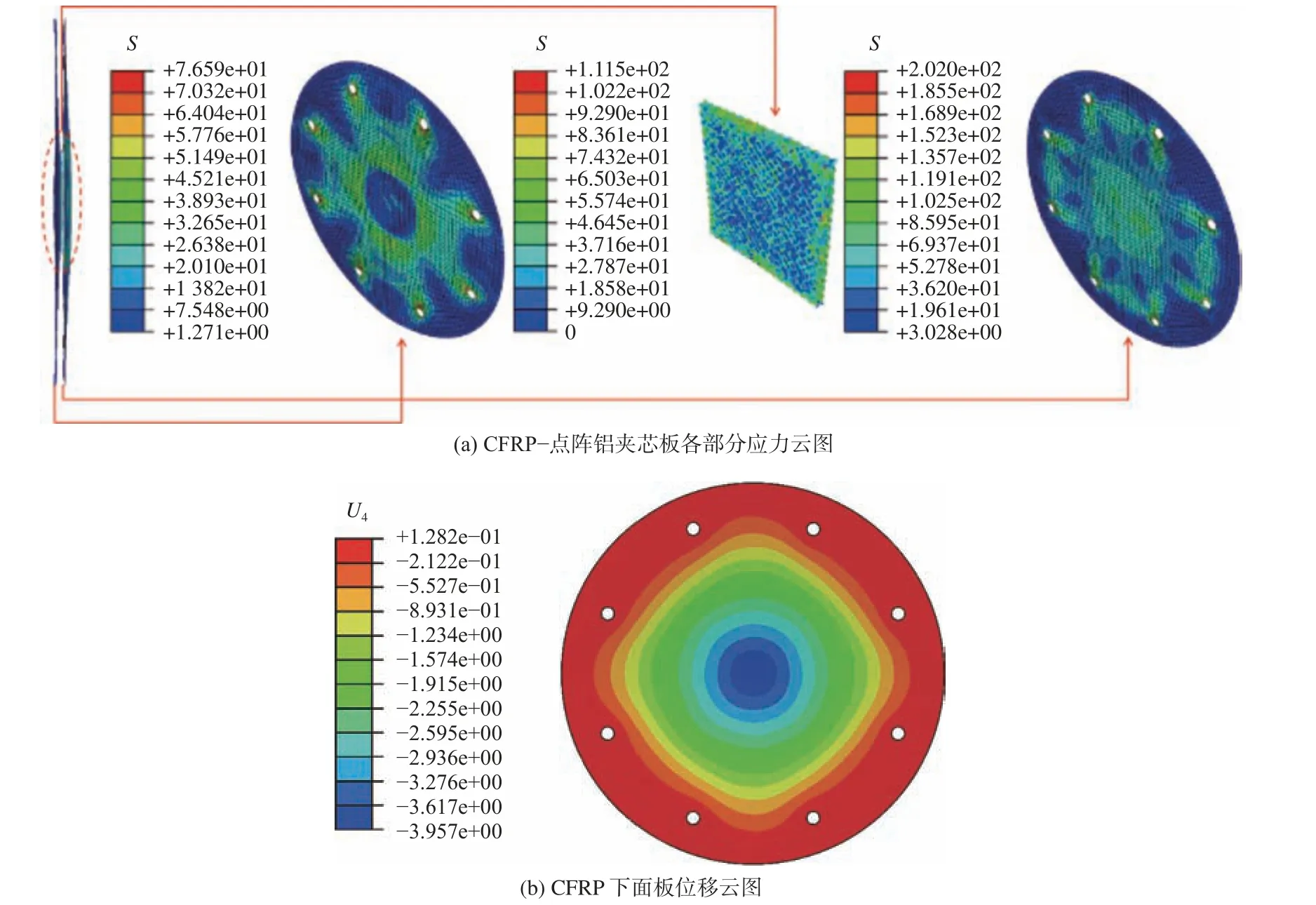
图8 CFRP 板的动力响应Fig. 8 Dynamic response of CFRP plate

CFRP 的耗能主要表现为基体开裂、纤维断裂和分层，其中夹芯的能量吸收以点阵材料的塑性变形存在，占总能量耗散的最大比例。一般来说，在所有条件相同的情况下，由于使用了更多的材料，具有较厚面板的结构其能量吸收性能会更好。因此，将通过分别改变上、下面板每层纤维厚度和Octet 点阵夹芯结构杆件直径，来探究其对动态响应的影响。

2.3 结构参数对动态响应的影响

2.3.1 上面板每层纤维厚度的影响

由于碳纤维复合材料板的制作工艺会限制面板的厚度，从理论上讲，只能通过改变层数来控制面板的厚度。为通过设计函数关系获得最优解，先假定面板的厚度可以连续变化，在确定理想最优解后，再根据工艺要求确定符合工艺条件的最优解。

保持Octet 点阵夹芯结构杆件直径和下面板厚度不变，改变上面板每层纤维的厚度，得到如表5 和图9 所示结果。由此可见，在所给3 种工况（工况A、工况B、工况C）条件下，无论是增加还是减小上面板铺层纤维的厚度，下面板的最大位移并没有发生很大变化，但对结构的能量吸收却有很大影响。此时，相比只改变上面板厚度的梯度结构，均匀结构有着更优的能量吸收性能。

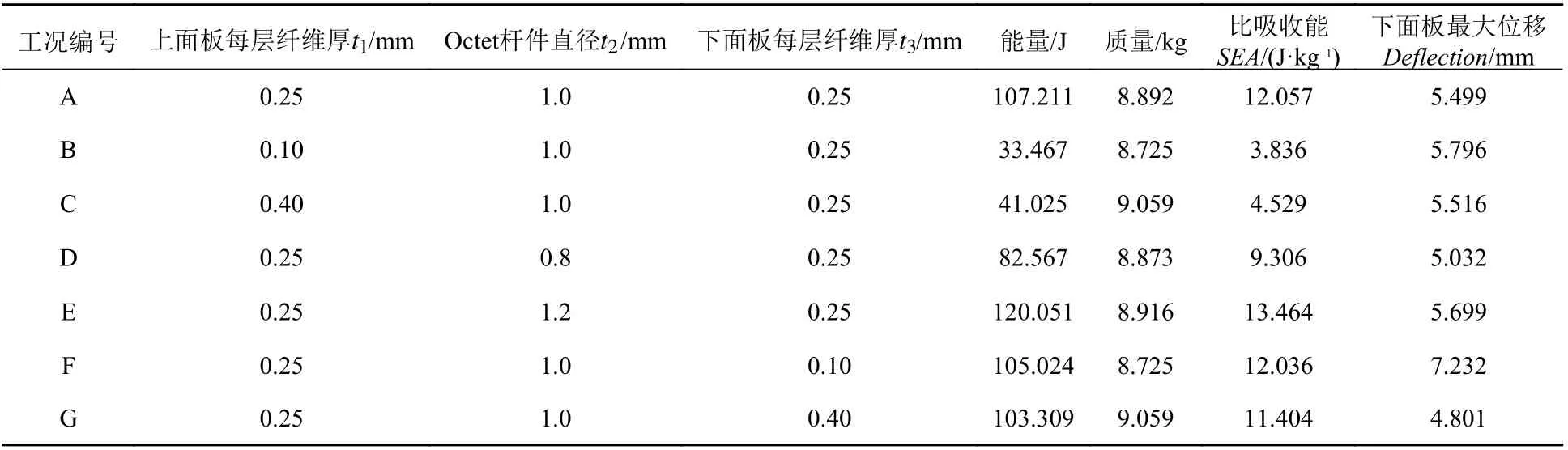
表5 不同工况下的仿真结果Table 5 Simulation results at different working conditions

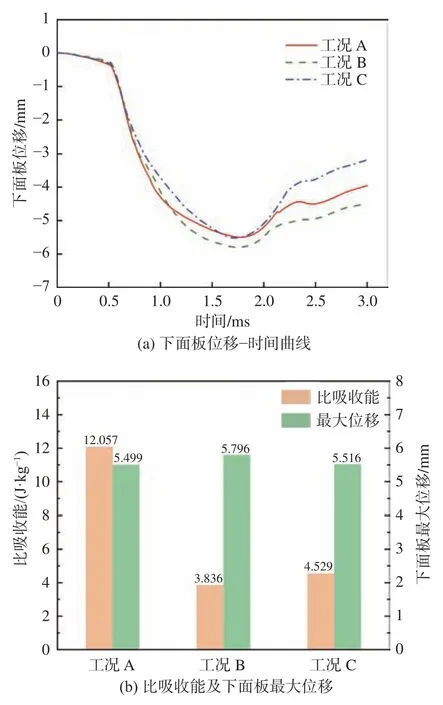
图9 改变上面板每层纤维厚度的仿真结果Fig. 9 Simulation results of changing the fiber thickness of each layer of the upper panel

2.3.2 点阵夹芯结构杆件直径的影响

保持上、下面板厚度不变，改变Octet 点阵夹芯结构杆件直径，得到如表5 和图10 所示结果。由此可见，在所给3 种工况（工况A、工况D、工况E）条件下，Octet 杆件直径对结构下面板位移的影响不是很大，但对结构的能量吸收性能有较大影响。这是因为随着Octet 杆件直径的增大，夹芯发生塑性变形的性能将大大增加，因此导致结构吸收的能量也更多。

图10 改变点阵杆件直径的仿真结果Fig. 10 Simulation results of changing the diameter of lattice rod

2.3.3 下面板每层纤维厚度的影响

保持Octet 点阵夹芯结构杆件直径和上面板厚度不变，改变下面板每层纤维的厚度，得到如表5 和图11 所示结果。由此可见，在所给3 种工况（工况A、工况F、工况G）条件下，下面板厚度对结构下面板位移的影响较大，而对结构的能量吸收的影响则较小。下面板厚度越大，发生的最大位移越小，但结构的能量吸收会下降。

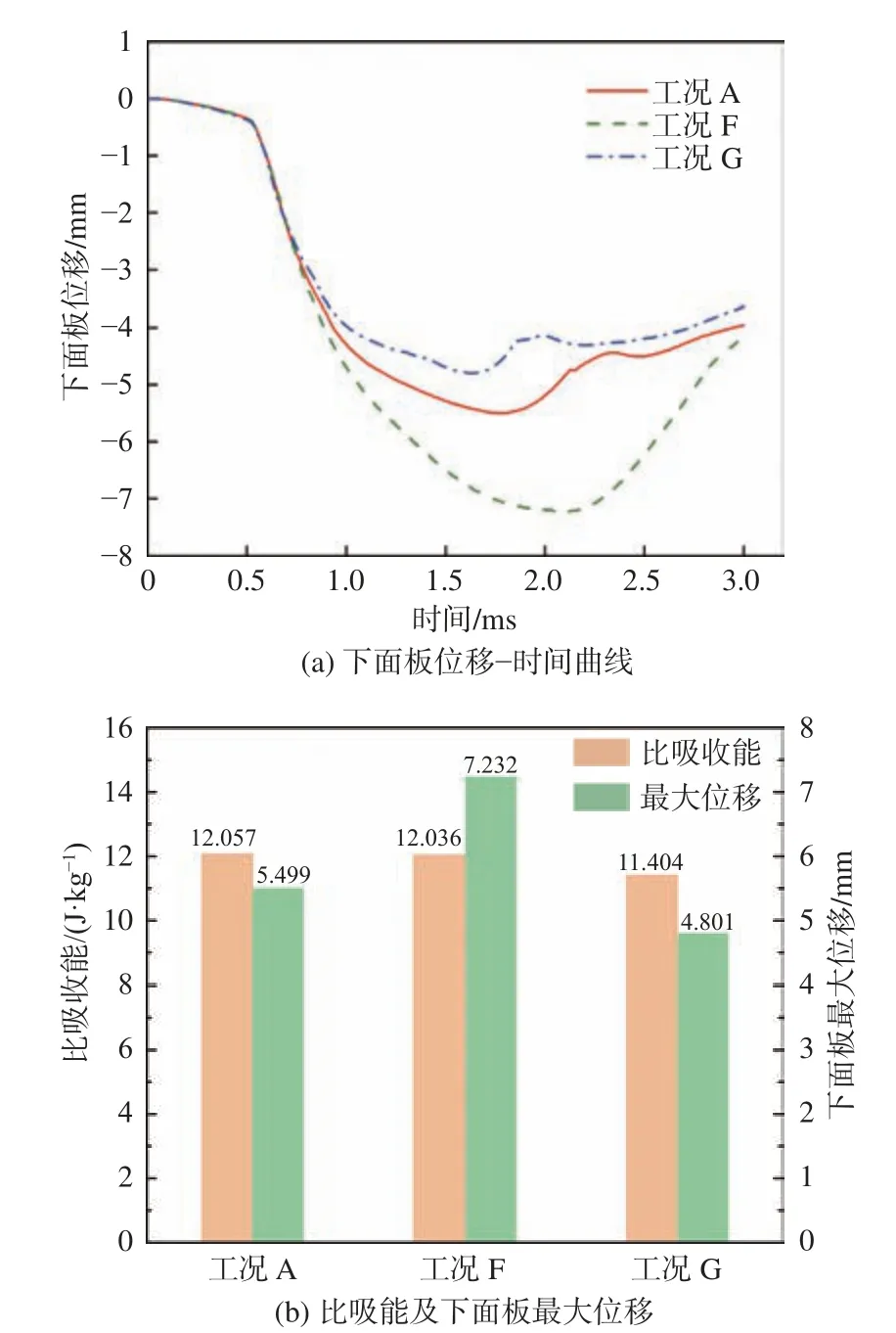
图11 改变下面板每层纤维厚度的仿真结果Fig. 11 Simulation results of changing the fiber thickness of each layer of the lower panel

综上所述，上、下面板厚度以及Octet 杆件直径对CFRP−点阵铝夹芯板的能量吸收性能和结构位移均存在影响。为更进一步探究3 种结构参数同时改变时模型动态响应的变化，并得到最优设计参数，需要采用实验设计方法。

2.4 CFRP−点阵铝夹芯板优化设计

对于质量相等的夹芯板，现有的研究[28]表明，在初始冲击速度不是很高的情况下，梯度结构（即厚度不均匀结构）相比均匀结构具有更加良好的能量吸收性能。不过，上、下面板厚度以及Octet 杆件直径这3 种结构参数对CFRP−点阵铝夹芯板能量吸收性能和结构位移的影响是相互作用的，为了更进一步探究3 种结构参数同时改变时模型动态响应的变化，得到最优设计参数，将利用响应面法对CFRP−点阵铝夹芯板进行能量吸收最优化设计。

2.4.1 能量吸收优化设计

将CFRP 上面板每层纤维厚度、Octet 杆件直径和CFRP 下面板每层纤维厚度作为设计结构变量，基于试验设计和代理优化软件LS-OPT 开展优化设计。采用拉丁超立方抽样的实验设计方法，得到15 种工况下上述参数与动态响应的代理优化模型如表6所示。

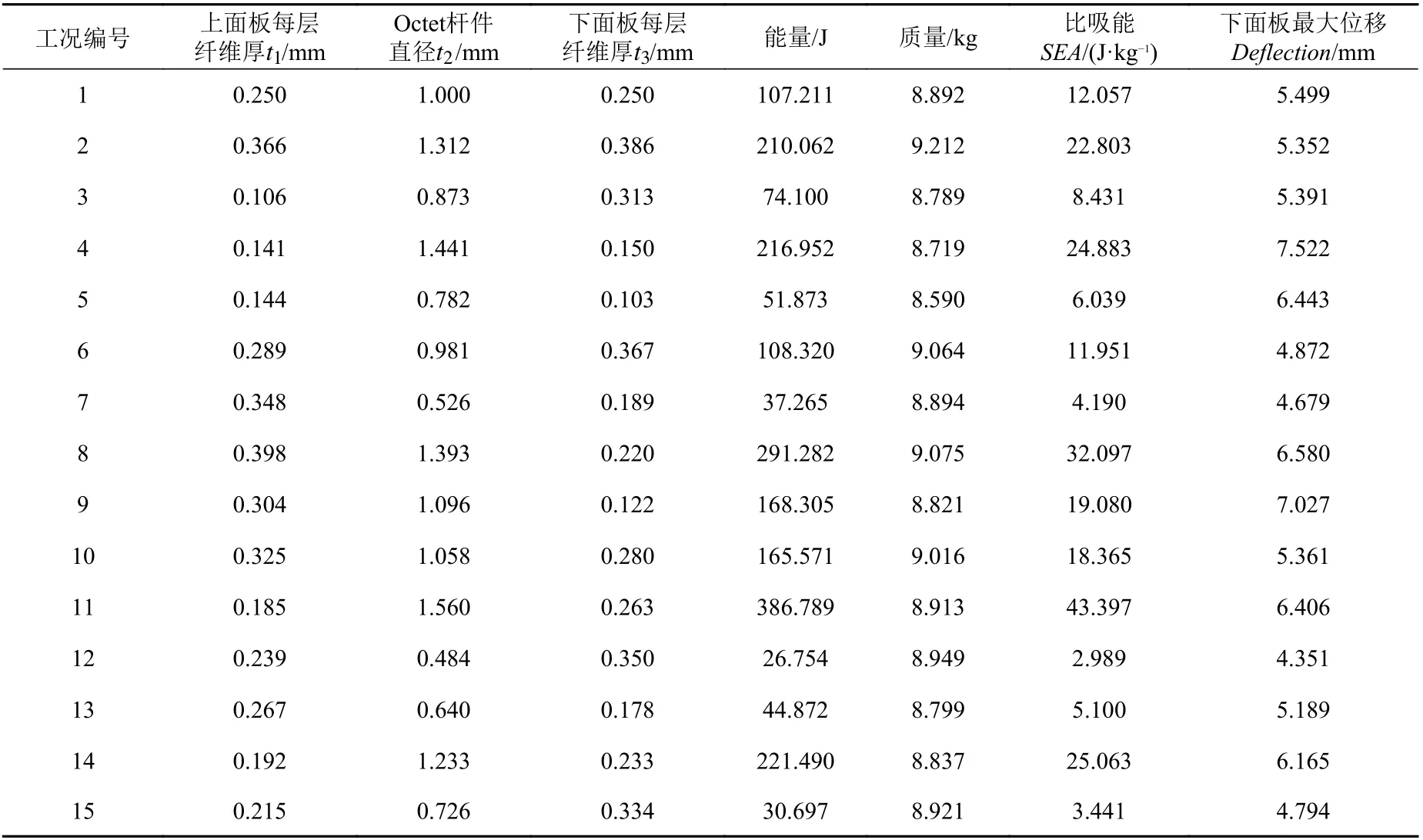
表6 实验设计代理优化模型及其仿真结果Table 6 Experimental design surrogate optimization model and its simulation results

采用回归分析的方法建立响应面模型，对CFRP−点阵铝夹芯板进行能量优化设计。首先，以上面板每层纤维厚t1、Octet 杆件直径t2和下面板每层纤维厚t3为设计变量，以结构的比吸收能SEA为优化目标，在满足上述设计变量及CFRP−点阵铝夹芯板质量恒定的约束条件下，求解SEA的最大值。SEA优化问题的约束条件如下：

利用Design-Expert 软件，采用二阶多项式对仿真数据点进行曲面拟合，得到拟合公式如下，其部分近似响应面如图12 所示。

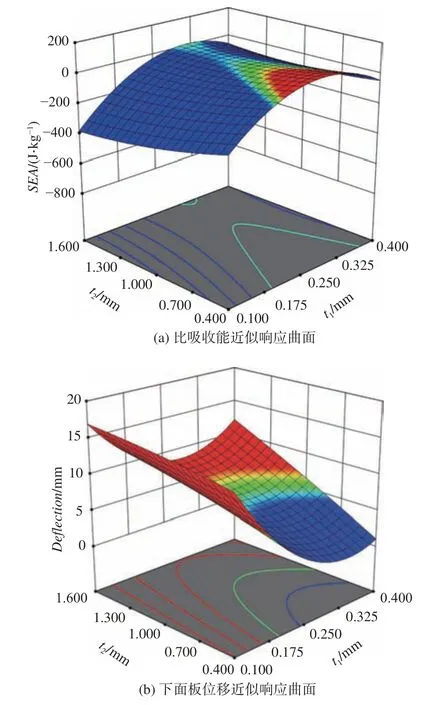
图12 响应曲面Fig. 12 Response surface

利用Mathematica 软件求解在约束条件下的比吸收能最大值，得到相应的最佳设计点（0.317,1.6, 0.1），预测的最优SEA和Deflection分别为45.300 J/kg 和8.757 mm，如表7 所示。然后，在最佳设计点进行验证分析，得到最优设计的SEA和Deflection分别为46.287 J/kg 和8.327 mm，误差分别为2.18% 和4.91%。优化结果表明，当下面板厚度取最小值且Octet 杆件直径取最大值时，SEA达到最大。优化设计的SEA值相比均匀设计的SEA值高284%。但也可以看到，此时下面板的挠度相比最初的设计高了51.4%。

表7 能量吸收优化设计及模拟结果Table 7 Optimization design and simulation results of energy absorption

2.4.2 能量吸收及变形优化设计

上述能量吸收优化设计的优化结果表明，减小下面板厚度有利于提高夹芯板结构的能量吸收效率。在舰船的局部防护方面，不能仅关心能量吸收问题，板的大变形位移也应重点予以考虑。因此，本节将在上节的基础上分析下面板变形的优化问题。这里，仍然将比吸收能SEA作为优化目标，在夹芯板结构的质量恒定为约束的前提下，附加下面板位移约束，令其小于最初设计的5.499 mm。此时，SEA优化问题的约束条件如下：

得到相应的最佳设计点为 (0.161, 1.115， 0.324)，预测的最优SEA和Deflection分别为18.367 J/kg和5.499 mm，如表8 所示。然后，在最佳设计点进行验证分析，得到最优设计的SEA和Deflection分别为19.151 J/kg 和5.467 mm，误差分别为4.27%和−0.58%。

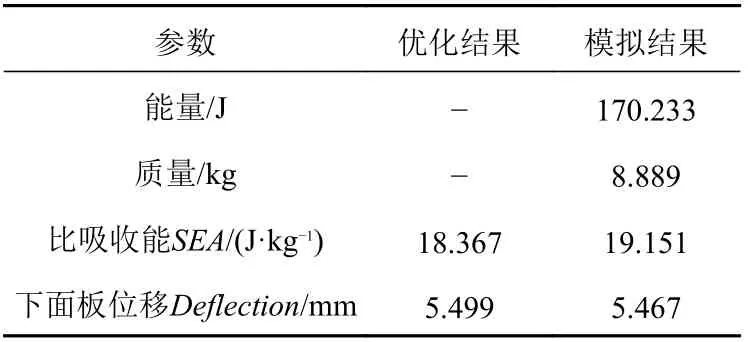
表8 能量吸收与变形优化设计及模拟结果Table 8 Optimization design and simulation results of energy absorption and deformation

图13 将2 种优化模拟结果与工况A 下的结果进行了对比。由图可以很直观地看到，在第1 种优化方式下，结构的能量吸收性能得到了很大提升；在第2 种优化方式下，在保证下面板变形不过大时，结构的能量吸收性能也提升了59%。

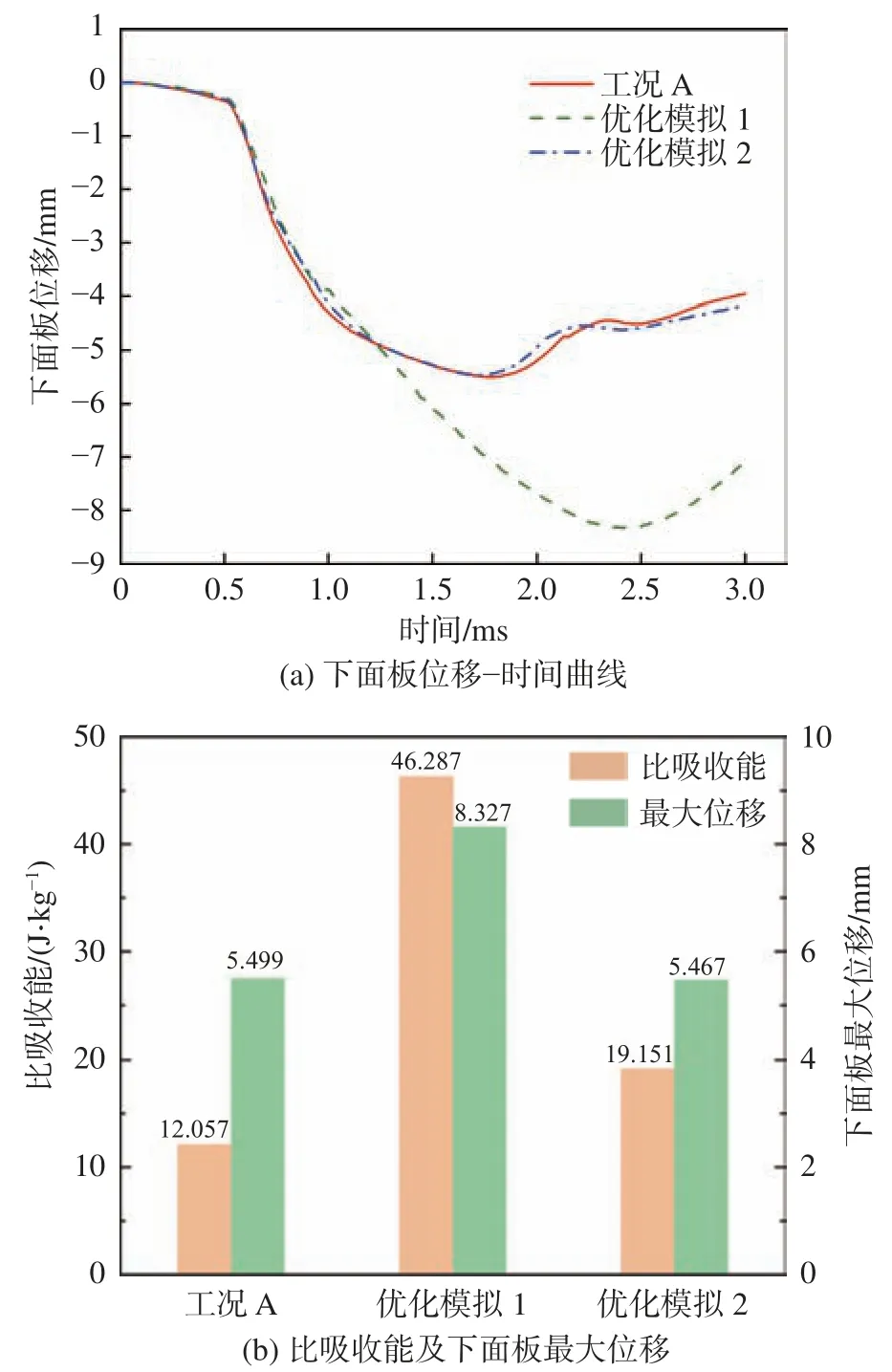
图13 优化模拟仿真结果Fig. 13 Optimization simulation results

3 结 论

本文以非接触水下爆炸冲击波载荷下夹芯板结构对舰船局部变形毁伤防护效果为背景，采用数值仿真方法对非药式非接触水下爆炸冲击波载荷特性进行探究。首先，研究了CFRP−点阵铝夹芯板在非接触水下爆炸冲击波载荷作用下的动态响应特点和整体动态大塑性变形过程。然后，通过实验设计的方法开展优化设计，得到了结构设计参数与变形响应的代理优化模型，分析了不同参数与目标函数的相关性。最后，基于防护要求和约束条件求解优化问题，得到了最优设计方案。主要得到如下结论：

1） 本文采用数值仿真方法对等效非药式非接触水下爆炸冲击波载荷特性进行探究，经与已有文献中实验结果的比较显示吻合较好，可为舰船局部结构的抗冲击性能研究提供可靠的方法。

2） 选取上面板每层纤维厚度、Octet 杆件直径以及下面板每层纤维厚度这3 种结构设计参数探究其对CFRP−点阵铝夹芯板能量吸收性能的影响，发现相比非梯度结构，梯度结构具有更加良好的能量吸收效果，且点阵结构杆件直径越大，结构的能量吸收性能提升越显著。

3） 利用响应面法对CFRP−点阵铝夹芯板的能量吸收进行优化设计，在板质量恒定的条件下，通过选取合适大小的上述3 种设计参数建立代理优化模型进行求解，得到了一组关于上面板厚度、Octet 杆件直径、下面板厚度的最优设计，其与数值模拟结果的对比验证了优化结果的可靠性。研究表明，同时增加上面板厚度，减小下面板厚度以及增加点阵材料的直径，存在一个最优尺寸的3 种设计参数，可使结构抗冲击性能最优。