蜂窝夹芯板等效方法在机翼刚度计算中的应用

谯盛军,王 飞，焦 瑾，刘 璐

(西安航空学院 飞行器学院，西安 710077)

0 引言

复合材料蜂窝夹层结构是由上下两层高强度的复合材料层合板和中间夹着的一层厚而轻蜂窝状夹芯层组成。以往针对复合材料蜂窝夹芯结构的研究大都是限于对单独的蜂窝夹层结构运用解析或数值方法分析，而对于含有蜂窝夹层板复杂结构进行解析或者数值分析的难度很大，且目前通用的有限元软件还没有提供专门的蜂窝单元可供选择，因此采用有限元软件对复合材料蜂窝夹层结构进行分析需要采用特殊的方式进行。

目前普遍采用蜂窝芯层等效方法，即用理论计算得到蜂窝夹层结构的等效力学模型，利用有限元软件近似模拟蜂窝夹芯结构。在刚度计算方面，利用相关理论简化机翼横截面的方法计算机翼横面刚度受到广泛关注，该方法在工程设计上较为高效和实用。本文基于蜂窝夹芯板等效方法，利用MATLAB软件对蜂窝夹芯机翼蒙皮进行材料的等效计算，将等效后的各向异性材料参数作为机翼剖面刚度计算的输入参数，并采用FORTRAN语言编程进行机翼刚度的计算。

1 蜂窝夹芯结构等效理论

蜂窝板动态等效理论是将整个蜂窝夹层板等效成等刚度、同尺寸的正交各向异性板，同时考虑了表层和夹层的面内和面外力学特性，推导出等效力学模型的参数，可为通用有限元程序提供必要的输入参数。图1所示为蜂窝夹层板(图1a)和等效板(图1b)的示意图。由图1a可知，夹层板表层比较薄，其厚度()明显小于夹芯层的厚度(2)。由图1b可知，蜂窝夹芯板等效板的厚度为2(+)，与蜂窝夹层板厚度相等。此外，等效板为各向异性板。

图1 蜂窝夹层板(a)和等效板(b)示意图

图2中左图所示为蜂窝夹芯层实物图，由该图可知，夹芯层由大小相近的六边形组成。根据蜂窝夹芯层结构的重复性，为分析问题简便，可将蜂窝夹芯层的结构抽象为六边形单胞模型进行分析，其示意图如图2右图所示，图中的和为胞壁长度；为胞壁与方向的夹角。

图2 蜂窝夹芯层实物(左)和单胞模型示意图(右)

根据Gibson理论求得的蜂窝夹芯层等效弹性常数如表1所示。表1给出了蜂窝单胞模型为六边形的等效正交各向异性板的弹性常数、、、和剪切模量。表中为夹芯材料的弹性模量；为惯性矩；为蜂窝夹层板的厚度。当蜂窝单胞模型为工程中常用的正六边形时，=且=30°，等效各向异性板的各项弹性常数也示于表1。

表1 蜂窝夹芯层等效各向异性板的等效弹性常数

富明慧等在Gibson理论的基础上研究了考虑蜂窝伸缩变形对等效弹性常数的影响，所得到的等效弹性常数如表2所示。

表2 考虑蜂窝伸缩变形的蜂窝夹芯层等效弹性常数

由哈密顿原理可以求出蜂窝夹层板和等效板具有相同形式的动力学基本方程，根据刚度等效和惯性等效方法，可以确定出等效板的物理常数为

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

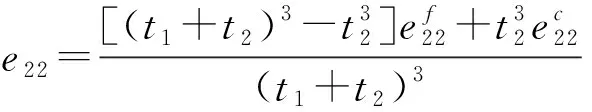
(9)

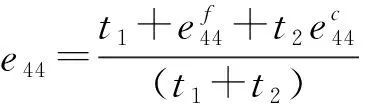
(10)

(11)

(12)

式中：上标和分别表示表层和夹芯层；为刚度系数，由以下表达式求解：

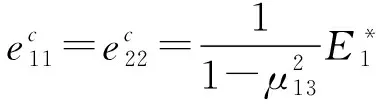
(13)

(14)

(15)

(16)

(17)

(18)

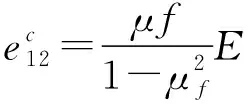
(19)

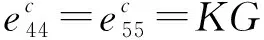
(20)

(21)

式中：为蒙皮层横向剪切影响程度的影响系数，根据工程实际或试验取值；和分别为蜂窝芯层上下面板材料的工程常数。

密度可由下式计算

(22)

式中，和分别为表层材料和蜂窝夹芯的质量密度。

根据式(1)～(22)可对六边形蜂窝夹芯层结构进行等效分析。

2 蜂窝夹芯蒙皮等效计算

利用MATLAB软件编写蜂窝夹层蒙皮等效程序，计算蜂窝夹层蒙皮等效后的弹性常数。针对某机翼模型，进行了蜂窝夹芯蒙皮的等效计算。计算所需参数如表3所示。

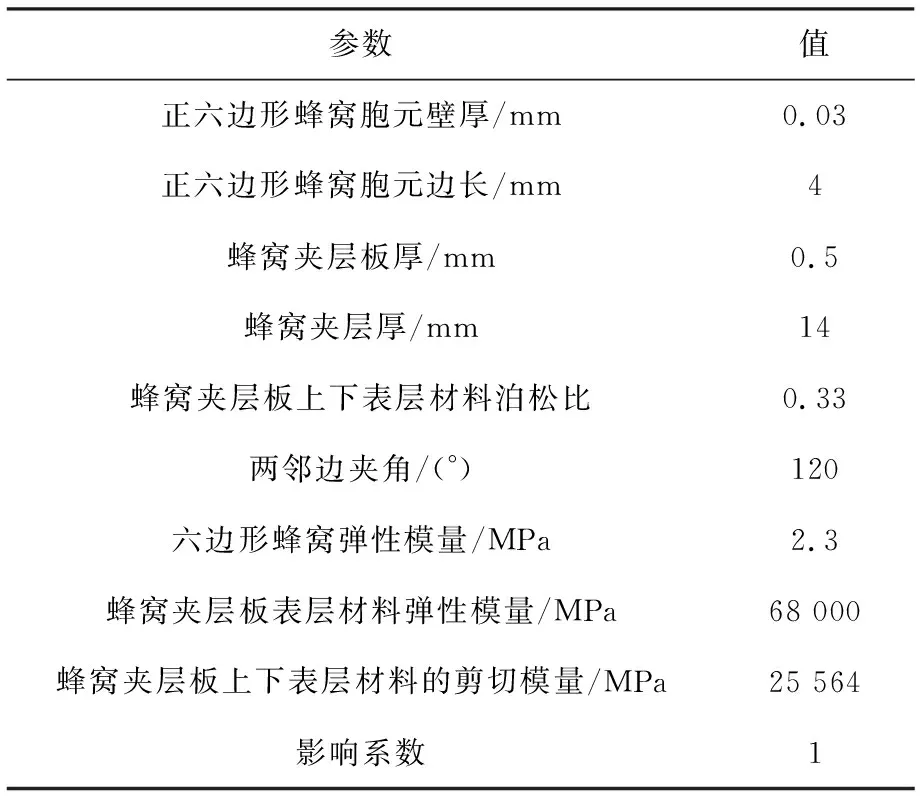
表3 蜂窝夹芯蒙皮等效计算输入参数

根据表3中的参数，利用蜂窝夹芯板等效方法，将蜂窝夹芯蒙皮等效为各向异性板，通过编程计算得到的蜂窝夹芯蒙皮的等效参数(见表4)。这些等效参数可作为机翼剖面刚度计算的输入参数。

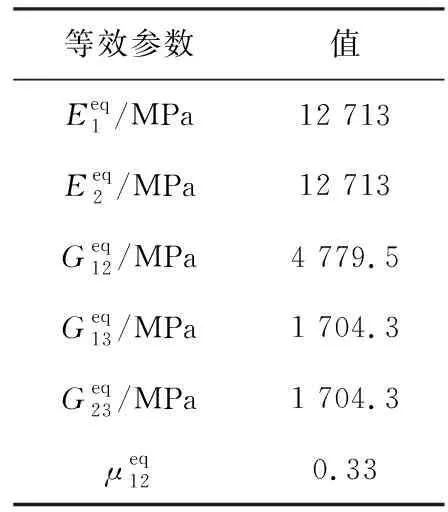
表4 蜂窝夹芯机翼蒙皮的等效弹性常数

3 蜂窝夹芯机翼刚度计算

根据前述蜂窝夹芯蒙皮等效各向异性板的参数，结合机翼剖面的静矩、惯性矩和等效后的剖面面积计算方法，对某型飞机的机翼从翼根到翼尖沿展向的机翼剖面刚度进行计算。计算采用文献[8]和[9]中的机翼剖面简化方法。

根据机翼剖面刚度计算理论，利用FORTRAN语言编写机翼剖面刚度计算程序，对选取的机翼剖面进行刚度计算，得到机翼不同剖面的刚度计算结果，在此基础上可知该机翼从翼根到翼尖沿展向的刚度分布。计算共选取了15个剖面，计算所得的从翼根到翼尖各剖面的弯曲和扭转刚度分布分别如图3和图4所示。

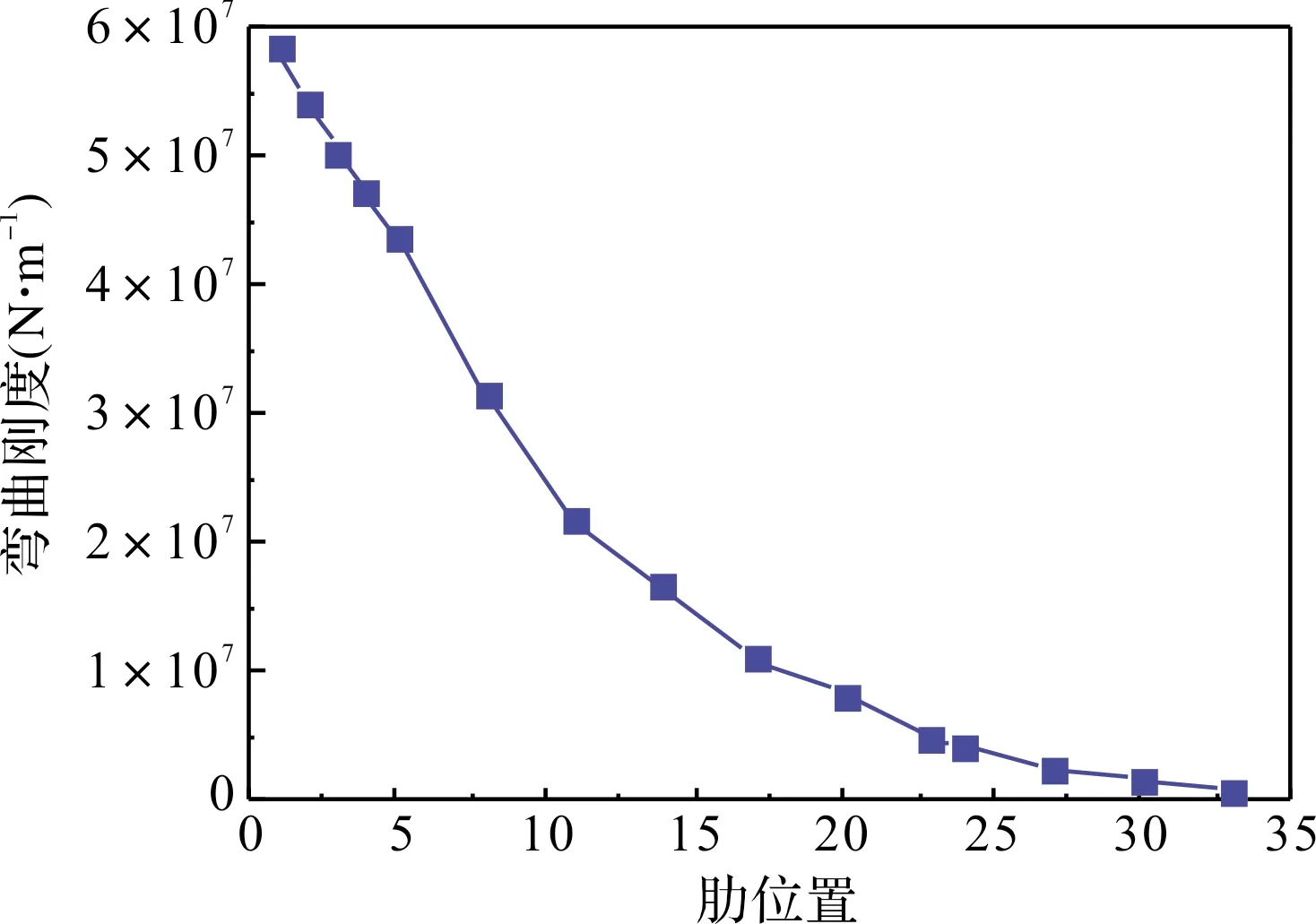
图3 蜂窝夹芯蒙皮机翼剖面弯曲刚度分布曲线

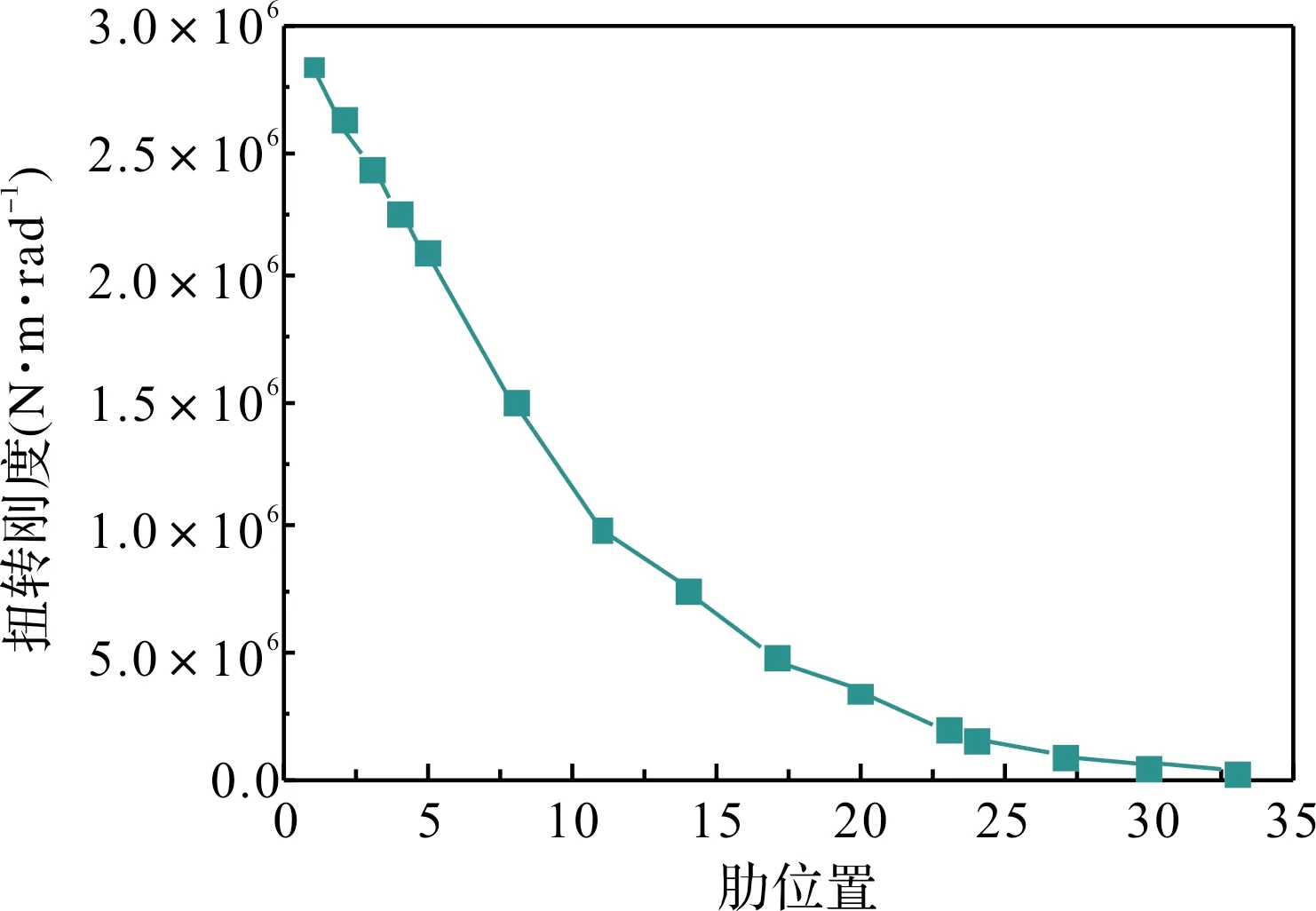
图4 蜂窝夹芯蒙皮机翼剖面扭转刚度分布曲线

由图3和图4可见，沿翼展方向弯曲和扭转刚度不断减小，且减小速度都由快到慢。其主要原因在于从翼根到翼尖，翼剖面面积和蒙皮厚度不断减小，桁条数量的减少，扭转刚度和弯曲刚度均逐渐减小。对比图3和图4可知，弯曲刚度的减小速度更快，表明相比于扭转刚度，梁截面的大小对弯曲刚度的影响更大。

4 结论

本文以蜂窝夹芯蒙皮结构为研究对象，基于蜂窝夹芯板等效方法，利用MATLAT开展了蜂窝夹芯蒙皮等效计算；基于机翼剖面简化方法和刚度计算理论，利用FORTRAN开展了机翼剖面刚度计算，得到了某型飞机机翼沿展向的刚度分布曲线。结果表明沿翼展方向弯曲和扭转刚度不断减小，减小速度都由快到慢，且弯曲刚度的减小速度更快。本文的方法可为工程上在强度和刚度分析与设计方面提供参考和借鉴。