上浮式水面发射筒弹射内弹道特性

曾培高，姜毅，杨哩娜

(北京理工大学 宇航学院，北京 100081)

0 引言

上浮式水面发射筒是一种新型导弹发射系统，其工作原理是，发射筒在深水区域释放，受浮力作用向水面运动，当发射筒的筒盖到达水面时，整个发射系统获得一定的出水速度，然后打开筒盖，采用燃气弹射方式将导弹发射出筒，使导弹获得一定的出筒速度，当导弹运动到水面一定高度后，导弹上的发动机开始启动工作。这种发射系统能够充分利用发射筒在水下的浮力势能，大大节省导弹的出水助推能量，因此这种发射系统具有结构简单、隐蔽性强等优点，而且可以在水下进行区域阵地布置，具有很强的战略意义。水面发射过程中，发射筒处于浮动状态，受到水的复杂作用力，不同于地面发射时发射筒处于固定状态，水面发射的弹筒相对运动过程不同于地面发射的弹筒相对运动过程，这将直接影响发射筒弹射内弹道性能，进而影响导弹的打击精度，甚至当导弹的出筒姿态与出筒速度达不到要求时，会引起导弹点火失败、姿态失稳进而导致自毁。

随着燃气弹射技术的广泛应用，不同应用下的燃气弹射内弹道问题得到了国内外研究人员的关注和研究，其中研究方法普遍采用理论与实验相结合的方法。燃气弹射的概念最早由McKinnis等提出。袁曾凤采用经典内弹道理论建立了高、低压室相似准则和内弹道方程。杨珺凡等围绕水下弹射过程，利用Realizable-湍流模型的计算流体力学方法和嵌套动网格技术，对水下弹射过程筒口气泡发展进行了仿真分析。唐垚等针对多级活塞缸式的新型燃气弹射发射方式，采用动态网格分层技术模拟导弹的运动，对活塞缸的展开过程、流场变化以及内弹道特性进行了研究。邱海强等以潜射导弹为研究对象，利用动网格技术和Mixture模型对导弹弹射出筒后筒口气泡的发展情况进行了研究，探究了筒口气泡扩张、收缩和拉断的一系列过程。高贤志等对自力发射的发射箱燃气排导方案进行了分析，设计了弹箱间隙直接排导方案。傅德彬等采用计算流体动力学(CFD)方法，分析了内外筒间隙大小对同心筒自力发射排气的影响，并提出优化设计方案。陈舟等讨论了不同水深对水下发射装置的最大膛压以及弹丸出膛速度的影响，提出了不同水深下的内弹道计算方法。周鹏等使用Spalart-Allmaras湍流模型，采用动网格技术，对弹丸在高压气体作用下的运动规律进行了研究。胡晓磊等、李仁凤等、胡晓磊等采用Realizable-湍流模型、动态网格分层技术和有限速率/涡耗散模型，分析了燃烧产物特性对燃气弹射内弹道的影响。赵谢等为了消除低温燃气弹射的压力双峰问题，对环形腔结构进行了优化。孟艳等研究了装配姿态偏差等对导弹离台姿态的影响。徐勤超等对水下提拉缸发射轻型鱼雷的过程进行了模拟。牛钰森等针对一种单提拉杆活塞气缸式弹射发射装置，研究了导轨排气孔对发射箱内流场的影响。这些研究为上浮式水面发射筒弹射内弹道性能研究提供了良好的研究基础，然而上浮水面发射筒弹射过程的核心问题，即燃气从弹筒间隙泄漏问题以及发射筒在水面浮动问题，其相关研究较少。本文提出了一种新型的导弹发射系统，即上浮式水面发射筒，对弹射内弹道涉及发射平台浮动与燃气泄漏问题进行了深入研究。

上浮式水面发射筒的发射过程中，发射筒在燃气和海水的共同作用下运动，筒内的燃气隔离板直接受到燃气的推力作用，进而带动弹体运动。由于加工装配要求，发射筒内壁与隔离板有一定的间隙，燃气会从间隙中泄漏，整个发射过程中间隙内的流动会变得复杂，存在亚音速流和超音速流的转化现象，使得零维内弹道理论不能精确地预测低压室的压力。本文针对这类复杂流动问题，对地面固定发射筒发射与水面发射筒发射分别进行了数值研究，并对比分析了两种发射形式下弹射内弹道性能与发射筒的运动轨迹等。

本文基于Fluent软件，采用雷诺平均的瞬态Realizable-湍流模型，求解高压高温气体在筒内壁和隔离板间隙中的流动状态；采用动态网格分层技术，模拟发射筒和弹体的各自运动，并考虑了它们的运动对流动的影响；采用Mixture多相流模型以及非均匀初始条件和边界条件，模拟发射筒的浮力变化。计算结果表明，由于水面发射中发射筒具有相对较高的设定出水速度，水面发射弹体的出筒速度大于地面发射的出筒速度。

1 物理模型和计算方法

1.1 物理模型

上浮式水面发射筒的工作原理是，发射筒在深水区域释放后，受浮力作用向上运动，当筒盖运动到水面时，弹与筒具有共同的出水速度，此时筒盖打开，高压室开始工作，燃气开始推动隔离板和弹体一起向上运动。本文以高压室开始工作的时刻作为模拟的初始时刻，此时弹筒位置示意图如图1所示。上浮式水面发射筒由高压室、低压室、发射筒、底座、隔离板和4根导轨等组成。监测点为实验和数值计算的压力观测点，用于监测低压室内的压力变化，监测点位置随弹体一起运动，用于监测间隙附近的压力变化。由于导轨的使用，隔离板与发射筒内壁和导轨存在一定的间隙，其中最小间隙位于图1中-截面处。如图2所示，隔离板与导轨的间隙约占总间隙面积的30%，大于隔离板与筒内壁的最小间隙。

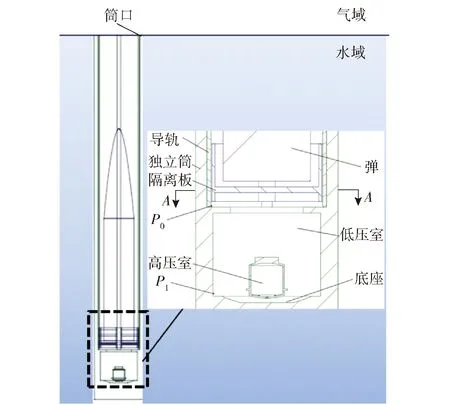
图1 发射筒发射结构示意图Fig.1 Schematic diagram of gas-ejection launcher

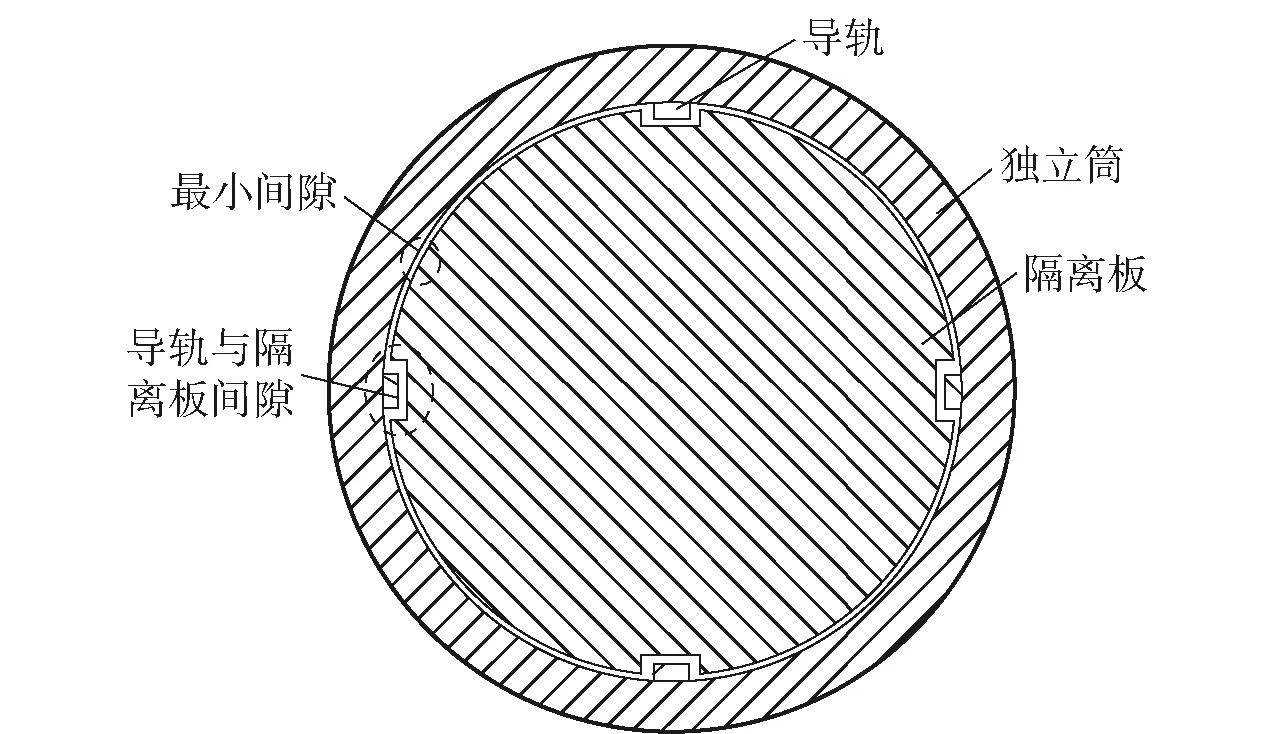
图2 最小间隙示意图Fig.2 Schematic diagram of minimum gap

1.2 计算方法

1.2.1 控制方程

由于发射筒不具有轴对称性，采用三维多组分Navier-Stokes(N-S)控制方程作为质量、动量与能量交换以及组分扩散的控制方程。其中：

质量交换方程即连续方程，形式为

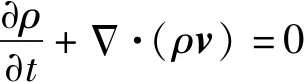
(1)

式中：为混合气体密度；为流动速度矢量。

动量交换方程为带有黏性流动的N-S方程，

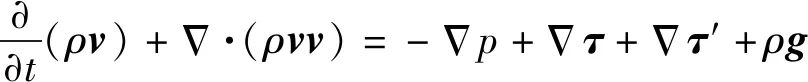
(2)

式中：为混合气体压强；为重力加速度，由于模型需要计算水对筒的作用力，液相的质量力不能忽略，重力加速度需要保留；′为湍流引起的雷诺应力张量，由湍流模型确定；为分子黏性引起的应力张量，

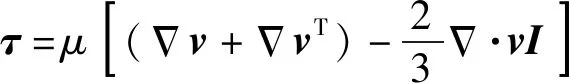
(3)

为分子动力黏性系数；为单位矩阵。

组分扩散方程为空气- 燃气双组分输运方程，求解组分的质量分数，

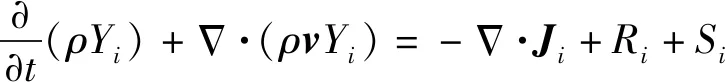
(4)

式中：为化学反应中组分的生成率，模型不考虑化学反应，为0；为其他相向组分转移的生成率，模型不考虑相变质量转移过程，因此该项为0；为组分的扩散通量，

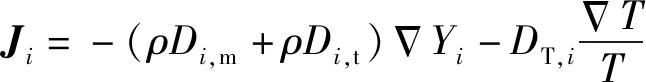
(5)

,m为分子黏性引起的组分质量扩散系数，,t为湍流引起的组分质量扩散系数，由湍流模型确定，T,为组分的热致扩散系数，为温度。

能量交换方程为总内能输运方程，由(6)式求解气体单位质量的总内能，

(6)

式中：为气体导热系数；为湍流引起的导热系数，由湍流模型确定；为组分的单位质量焓；为能量源项，模型中不加入相变传热过程，因此该项为0。

1.2.2 湍流模型

发射过程中，高压室内的燃气经过喷管进入低压室时会形成超音速射流，提高低压室的压力。随着低压室的压力升高，低压室内的燃气会从筒内壁和隔离板间隙中流出，发生二次射流现象。两次射流过程中均涉及壁面的流动分离过程。Realizable-湍流模型能够较好地模拟剪切流、分离流以及射流等现象，因此模型中采用Realizable-湍流模型模拟湍流效应。

1.2.3 多相流模型

在高压室工作的开始时刻，发射筒下方完全浸在水中，发射筒口与液面齐平。由于筒具有向上的运动速度，筒的运动为跨液- 气两相运动，筒的外表面既受到气相作用又受到液相作用，因此计算模型需要考虑多相流模型。筒内的燃气- 空气混合气体在出筒后可能会与筒口附近的液面发生作用，使得液相和气相发生交互。Mixture模型能够较好地处理相间交互作用，因此模型采用Mixture模型模拟发射阶段的两相运动过程。

1.2.4 导弹与发射筒的运动规律

弹射过程中，导弹在燃气推力的作用下沿着发射筒轴线向上运动。弹体在轴线方向上的受力有燃气推力、重力、弹体表面空气阻力和摩擦力。其合力的公式为

=---

(7)

而在计算开始时刻，发射筒具有向上的出水速度，在水面上悬浮运动。因此，筒在轴线方向上的受力有气体阻力、重力、水对筒的作用力和摩擦力。其合力的公式为

=--+

(8)

非定常计算到第个时间步时，导弹沿轴线方向的速度m,和位移m,、发射筒沿轴线方向的速度c,和位移c,分别由(9)式求得，其中Δ为计算时间步长。

(9)

式中：m,-1为第-1个时间步弹受到的合力。

仿真计算将(7)式～(9)式通过udf加载到Fluent软件中，动态计算弹、筒的受力、加速度与速度，采用动态分层技术对每个时刻的网格进行更新，模拟弹、筒在流场中的运动。

1.2.5 初边值条件与网格模型

由于模型中发射筒的运动涉及外流场的流动，计算域不仅包含高压室、低压室等内流场区域，而且包含由筒外水域和筒口上方气域组成的外流场区域。发射筒的几何模型虽然不具有轴对称性，但呈中心对称，因此可采用1/4模型对发射筒弹射过程进行模拟。计算域以及边界条件如图3所示。计算域的外边界除对称面外均为压力出口，内流场中高压室入口设为压力入口，作为燃气入口边界。弹、筒运动为沿同一方向的直线运动，适合使用动态网格分层技术模拟其在流场中的运动过程。动态网格分层技术模拟不同速度的多个运动体时，需要采用interface设置。因此，计算域中，包络弹的运动域与包络筒的运动域的共同面拆分为一对interface(interface 1)，包络筒的运动域与周围静止域的共同面拆分为一对interface(interface 2)。计算域中壁面条件均为绝热壁面条件。

图3 计算域及边界条件示意图(红色面为压力出口，绿色面为interface，黄色面为对称面，蓝色面为压力入口，灰色面为壁面)Fig.3 Computational domain and boundary conditions(The red faces are the pressure outlets,the green faces are the interfaces,the yellow faces are the symmetries,the blue face is the pressure inlets,and the gray faces are the walls)

由实验获得的压力入口的总压随时间变化曲线如图4所示，其中为高压室的参考压力，为燃气发生剂燃烧的参考时间。由图4可见：=0时，高压室的堵盖打开，高压室的压力约为02；=0033时，高压室的压力达到了第1个峰值，约为03；随后高压室压力降低，在=0154时压力曲线达到了第1个波谷，约为02；由于高压室装药为增面燃烧药，在=069时压力曲线达到了第2个峰值，约为098。

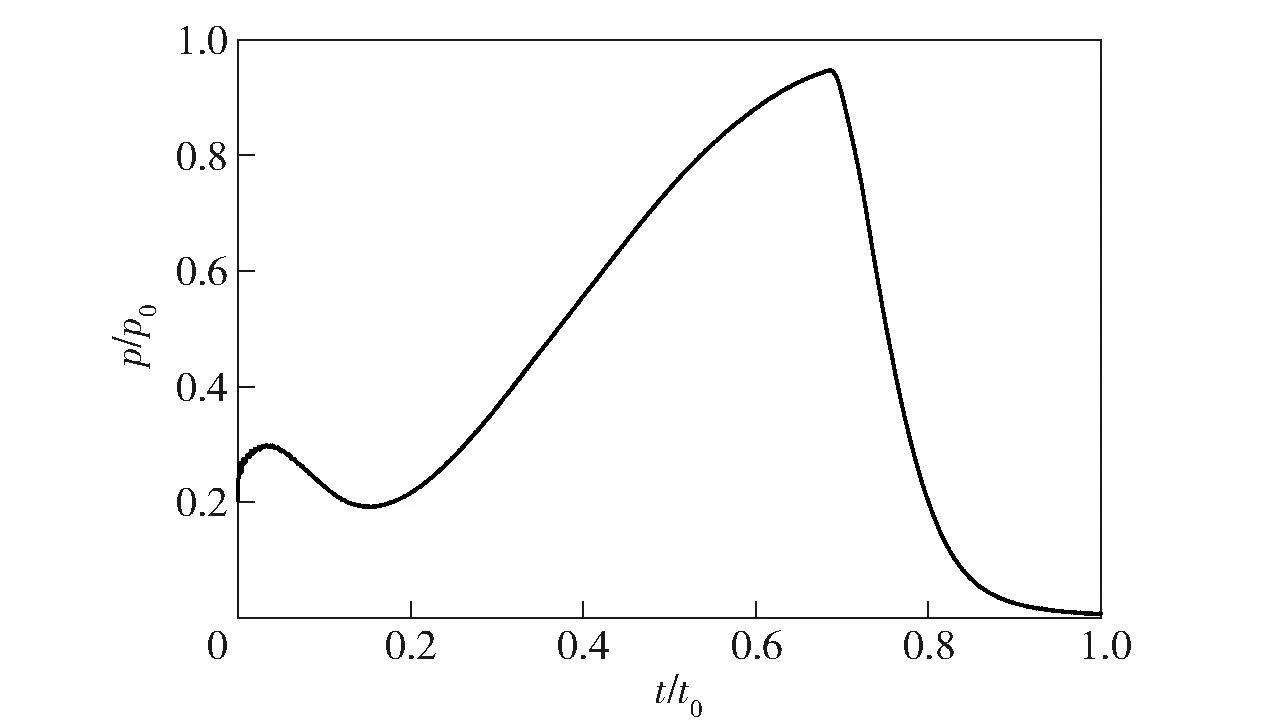
图4 高压室总压力曲线Fig.4 Total pressure of high pressure chamber

发射计算域的初始值分布如图5所示。从图5中可知，在计算开始时刻，筒口与气液交界面齐平；高压室的初始压力为冲开堵盖的压力，气域的初始压力值为大气压值，水域的初始压力随水深线性变化；在初始时刻，弹、筒具有相同的出水速度，方向向上。

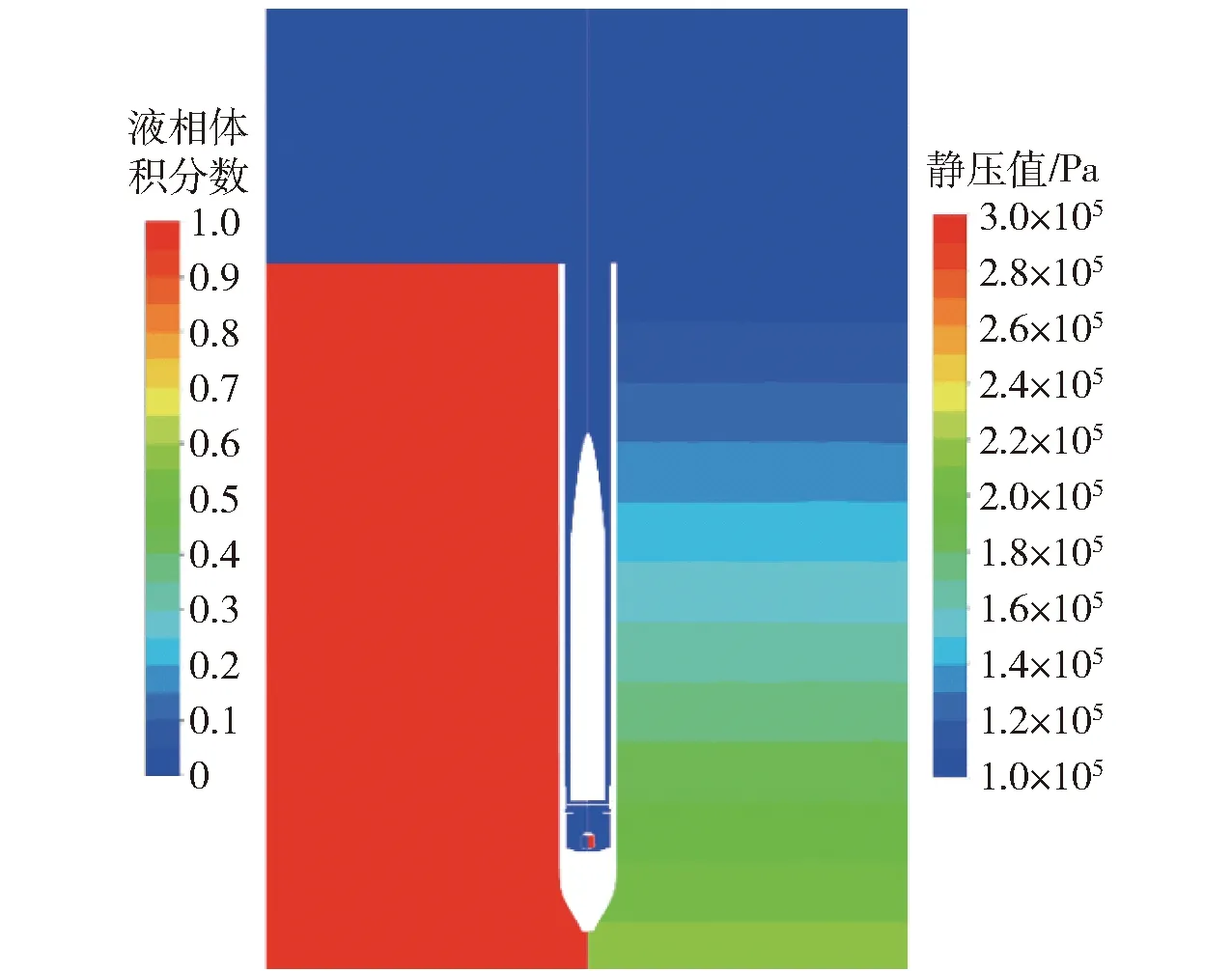
图5 计算域初始值分布云图Fig.5 Initial contours of water volume fraction and pressure

在建立网格前，对筒内壁与隔离板间隙的网格进行了无关性验证。图6为网格无关性验证曲线。为了验证网格的无关性，本文对4种不同间隙网格尺度的工况进行了数值模拟，分别为0.5 mm、1 mm、2 mm和3 mm。间隙网格尺度为Δ，弹的出筒速度为Δ。图6中，Δ为间隙网格尺度临界值。从图6中可以看出，在间隙网格尺度为2 mm即取临界值时，出筒速度的相对误差梯度出现阶跃性降低，其相对误差在0.8%内，同时该尺度下筒内间隙的平均温度开始趋于一致。因此，间隙网格尺度设定为2 mm。为了保证运动过程中interface上配对的网格尺度相近，计算域的网格数约为590万。

图6 网格无关性验证曲线Fig.6 Mesh size independence verification curve

2 数值方法验证

为验证本文数值方法的可靠性，对发射筒做了地面实验。监测点的计算值和实验值对比如图7示，其中为实验参考压力。由图7可见：点处数值结果与实验结果的压力变化趋势基本一致。数值结果的第1个压力峰值为0610，实验值为0624，计算结果的第2个压力峰值为0835，实验值为0792；计算值与实验值在压力峰值上的误差在55内；实验中弹体出筒速度为767 m/s，数值计算中弹出筒速度为820 m/s，计算值和实验值在弹体出筒速度上的误差在7内。因此，从计算结果和实验结果的对比可以看出，采用本文所使用物理模型和数值计算方法能够有效地模拟发射筒的弹射过程。

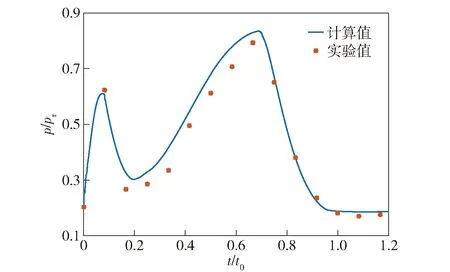
图7 P0点计算压力值与实验结果对比Fig.7 Comparison of numerical and experimental pressure results at Point P0

3 计算结果分析

3.1 内弹道特性分析

水面弹射启动前，弹体在发射筒内受到浮力作用一起向上运动，弹筒具有相同的向上运动速度。筒盖浮出水面后，筒盖打开，并且高压室开始工作，高压室的压力快速升高。高压室内的压力升高至破膜压力后，燃气冲开高压室的堵盖进入低压室内，低压室的压力升高。隔离板受到低压室的压力作用，产生向上的力，当隔离板受到的推力能克服隔离板、弹体以及适配器等的重力、弹体运动的空气阻力和适配器与筒接触产生的摩擦力时，弹体与发射筒开始做相对运动。由于隔离板与内筒壁有间隙，燃气将通过间隙从低压室进入大气环境中，在间隙中形成二次射流，并在附近形成复杂的波系结构，使低压室的压力产生较为复杂的变化。

地面发射与水面发射监测点、监测点的压力随时间变化曲线，弹体加速度、弹体速度增量Δ(即弹体速度与出水速度的差)随弹筒相对位移变化曲线以及弹筒相对位移随时间变化曲线如图8所示，发射筒的运动曲线如图9所示，其中为破膜时刻弹筒的共同运动速度(出水速度)，为弹体的参考加速度，为低压室的参考压力，为环境压力，为弹体出筒行程，=1101，=1171，为筒的位移，为筒的加速度。

由图8(a)可知，根据低压室的压力升降，可以将发射过程分为4个阶段，分别为段、段、段以及段，为计算初始时刻，点在=008左右，点在=024左右，点在=069左右，为弹出筒时刻。

在段，点时刻高压室的堵盖冲开，高温高压燃气充入低压室，并压缩低压室的剩余空气，低压室的压力快速传播并升高。由图8(d)可知，在段，水面发射与地面发射中弹、筒没有明显的相对位移，二者低压室的容积几乎没有变化，而且二者高压室采用同一压力曲线，因此二者低压室内的流动几乎相同，同一监测处的压力也几乎一致，如图8(a)中段所示。对比图4可知，监测点出现第1个压力波峰的点时刻出现高压室的第1压力波峰与高压室的第1压力波谷之间，此时表压值约为052，表明在低压室的压力到达第1个压力波峰时刻，高压室向低压室补充的燃气出现了减少。由图9(a)可知，在时刻，筒受到向上的正浮力作用，随后低压室压力升高，发射筒受到低压室的下压作用，筒向上做减速运动。

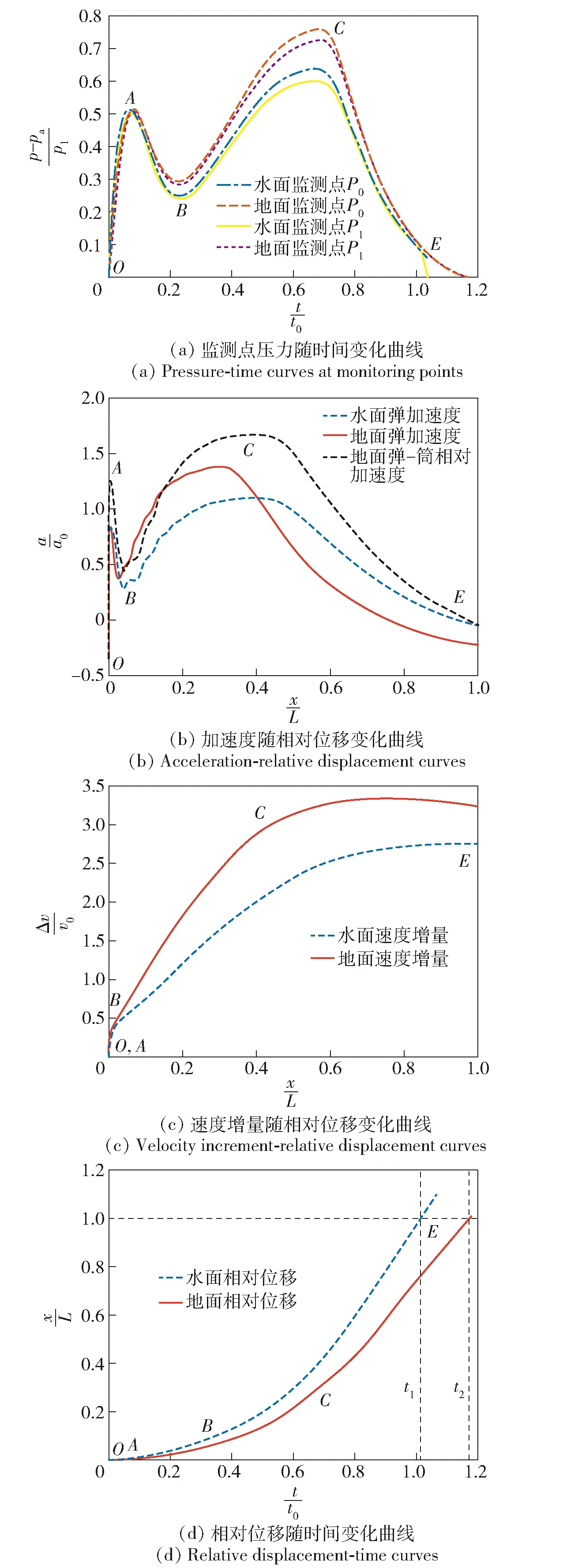
图8 水面发射和地面发射内弹道曲线Fig.8 Interior ballistic curves of launching on ground and water-surface

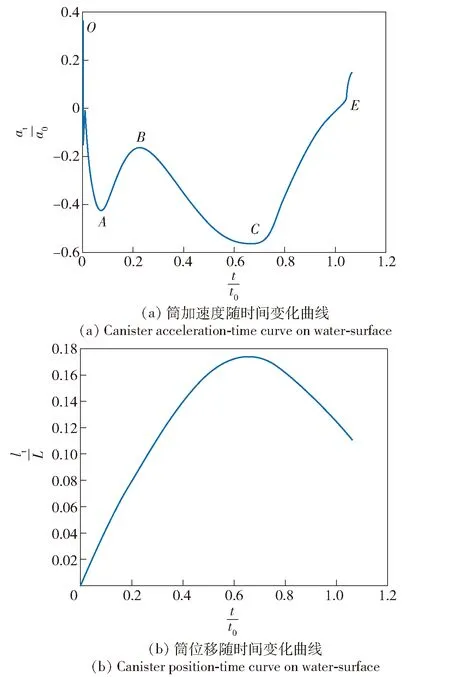
图9 筒运动曲线Fig.9 Motion curves of canister on water-surface

在段，弹筒开始有明显的相对运动，弹体相对运动使低压室气体出现明显膨胀。点时刻位于高压室的第1个压力波谷与第2个压力波峰之间，因此在段高压室的压力先降低后升高。由于高压室的压力先降低，低压室内补充的燃气出现减少，但弹筒的相对位移在加速变大，使得低压室内的气体膨胀加剧，进而低压室压力出现降低，弹体的加速度也随之减小。在这一阶段，水面发射与地面发射中低压室压力具有相似的下降趋势。由于点靠近高压室，其燃气压缩效应要强于燃气膨胀效应，而点靠近相对运动的隔离板处，其燃气膨胀效应要强于燃气压缩效应，使得点的压力高于点的压力。由图8(b)可知，水面发射弹筒相对加速度大于地面发射中弹筒相对加速度(即地面弹体自身的加速度)，在点时刻，水面发射中弹的加速度极小值029要小于地面发射弹的加速度极小值037，约小21，水面发射的弹筒相对位移0038 8要大于地面发射的弹筒相对位移0024 5，其低压室约多膨胀了58，这也表明了水面发射低压室的膨胀速度要大于地面发射的膨胀速度，水面发射低压室的压力降低得更快。因此，在时刻，水面发射低压室表压的极小值025要小于地面发射低压室表压的极小值029，约小14，如图8(a)中段所示。

段高压室压力一直处于上升趋势，即高压室向低压室补充的燃气一直在增多。在点，低压室内燃气的补充已经足够抵消燃气的膨胀作用与泄漏作用，低压室气体再次受到补充燃气的压缩作用，使得低压室压力再次升高，并在高压室压力达到第2个峰值的附近时刻，地面发射和水下发射的低压室压力几乎同时到达第2个峰值，即图8(a)中点附近。在点时刻，由于弹筒相对速度较大，隔离板附近的膨胀现象较为明显，监测点、的压力值出现明显的差异，二者的压力差约为其压力值的6。由图8(b)可知，在段，地面发射与水面发射燃气膨胀现象与段近似，在时刻，地面发射弹筒相对位移为0315，而水面发射弹筒相对位移为0412，约多膨胀了30，使得水面发射低压室的平均表压062低于地面发射低压室的平均表压0744，约低16，水面发射弹体的最大加速度约为110低于地面发射的最大加速度1374，约低20。这也使得在时刻水面发射弹体的速度增量比地面发射的速度增量小25，如图8(c)所示。

在段，高压室压力开始降低，直至降至环境压力。由于弹筒相对位移继续增大，低压室的气体膨胀作用逐渐占主导地位，监测点、的压力值逐渐贴近，同时随着弹体完全出筒，水面发射和地面发射筒内的压力都降至环境压力附近，监测点上的压力也就趋于一致。由图8(d)可知，水面发射弹体的出筒时间=1013要快于地面发射的出筒时间=1171，约快16。由图8(c)中可知，水面发射弹体的出筒速度增量小于地面发射的出筒速度增量，弹体的动量增量约损失15。由于水面发射筒有初始出水速度，使得水面发射弹体的出筒速度为，大于地面发射弹体的出筒速度。由图9(b)可知，从高压室破膜后到弹体出筒过程中，虽然筒的运动一直受到燃气的阻碍作用，但由于其具有出水速度，其位移一直为正，使得筒口一直处于水面上方。

3.2 流场变化规律分析

由于高压室的压力与低压室的压力相差较大以及低压室的压力和环境压力也相差较大，复杂的波系结构主要存在于高压室喷管出口附近以及隔离板与筒壁间隙处及其出口附近，波系的变化可能会导致高压室的出口流量以及低压室的流出流量发生变化，进而影响内弹道的性能。

高压室的出口流量随时间变化曲线如图10所示，其中为参考流量。由图10可见：由于水面发射和地面发射采用相同的高压室条件，虽然二者低压室的压力存在明显差异，但在段，高压室压力足够大，喷管喉部马赫数一直等于1，因此在段喷管流量一直处于壅塞状态，二者高压室的出口流量几乎一致；在段，高压室的压力进入衰减阶段，虽然高压室喷管内流动存在超音速转向亚音速的转变过程，但高压室喷管内流动转为亚音速时，水面发射和地面发射低压室内的压力几乎趋于一致，因此整个发射阶段，水面发射和地面发射高压室向低压室内补充的燃气量是几乎相同的。

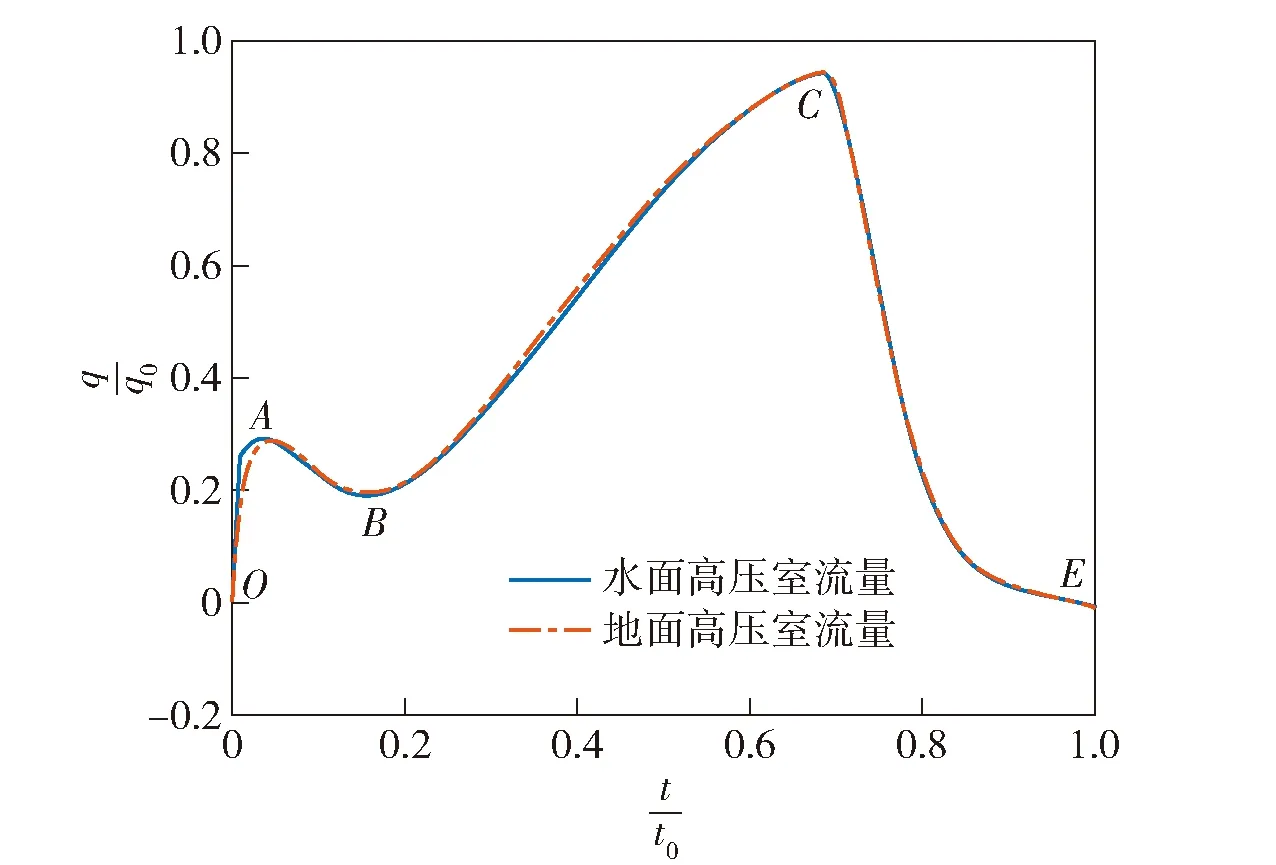
图10 高压室出口流量随时间变化曲线Fig.10 Mass flux in high pressure chamber on ground and water-surface

由于隔离板和内筒壁存在间隙，低压室内的气体受到高压室流入的燃气压缩后便会从间隙中流向外界环境中，并进一步膨胀。低压室的流出流量随时间变化曲线如图11所示。由图11可见：低压室的第1个流出流量峰值到达时刻与高压室的第1个压力峰值到达时相近，由图8(a)可知，此时水面发射和地面发射低压室的压力几乎一致，因此二者流出流量的第1个峰值也几乎一致，约为0095，约占流入低压室燃气流量的33；低压室的第2个流出流量峰值约在高压室的第2个压力峰值时达到，其流量约占流入低压室燃气流量的8。此时水面发射低压室的压力低于地面发射低压室的压力，因此水面发射低压室的流出流量小于地面发射的流出流量。虽然第1个峰值时低压室的压力低于第2个峰值时低压室的压力，但由于在第1个峰值时低压室流出的气体为常温空气，而在第2个峰值时低压室流出的气体为高温燃气，常温空气的密度远远高于高温燃气的密度，使得低压室的第1个流出流量峰值大于第2个流出流量峰值。

图11 低压室流出流量随时间变化曲线Fig.11 Mass fluxes in low pressure chamber on ground and water-surface

间隙处马赫数1等值图如图12所示。由图12可见：在=0017至=098时，最小间隙处流动一直处于超音速流动状态，即红色等值面包络了最小间隙，因此在这一阶段，低压室从最小间隙流出的流量也一直处于壅塞状态，壅塞时间约占总发射时间的95；由于隔离板与导轨的间隙要宽于最小间隙，且占总间隙面积的30左右，在整个发射过程导轨处间隙的流动在亚音速流动和超音速流动中反复变化。其具体变化有，在=008时导轨上端间隙刚好被红色等值面完全封闭，在=017时封闭该间隙的等值面发生破碎，在=035时该间隙再次被等值面封闭，在=083时封闭该间隙的等值面再次破碎。因此，在=008前、=017至=035以及=083后导轨间隙处的流动均有亚音速流，其时间约占总发射时间的45，其余时间处于超音速流动状态。由于导轨处间隙的流出流量比重较大，而且其处于亚音速流动状态占时较长，因此无法直接采用零维内弹道理论计算间隙的流出量，同时也无法采用二维等效模型精确计算出间隙的流出量，进一步表明采用三维计算的必要性。

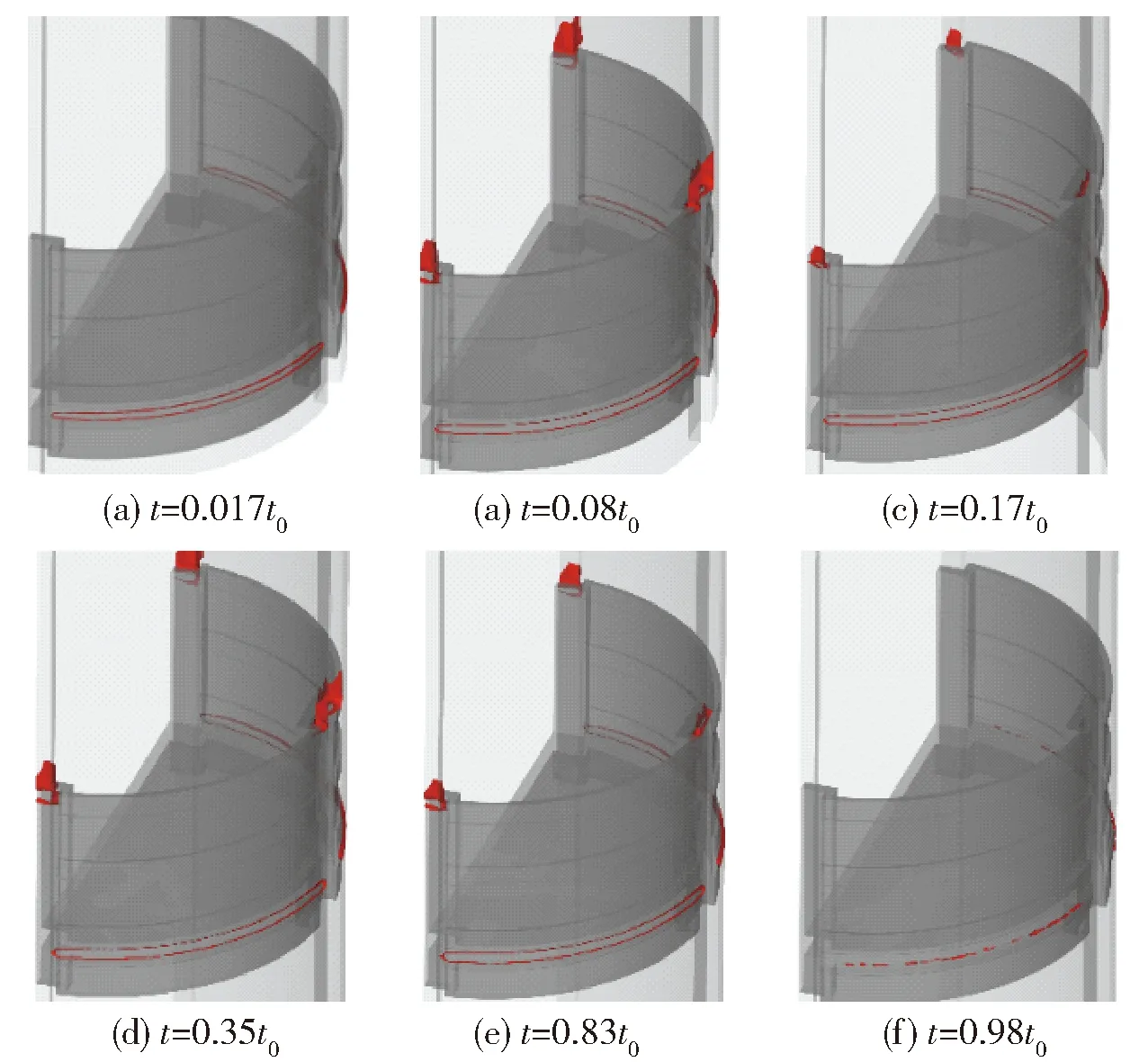
图12 间隙处马赫数1等值面图Fig.12 Mach=1 iso-surfaces at the gap on water-surface

水面发射筒口附近的流动如图13所示，左侧为速度矢量图，速度上限为20 m/s，右侧为温度云图，温度上限为370 K。从图13中可知，在=0325时，燃气开始从筒口溢出并直接向上方运动，此时筒口与气- 液交界面处有一定的距离，气- 液交界面处仅受常温低速的空气作用，该条件不足以引起相变发生。在低压室的压力到达最大时=069，以及隔离板快出筒时=10，从筒口流出的燃气一直保持向上运动，虽然燃气出筒口后发生了膨胀，但筒口远离气- 液交界面，燃气不会直接作用于液体表面，气- 液交界面处依然仅受常温低速的空气作用。因此，在水面发射过程中，由于在燃气流出筒口时筒口已远离气液交界面，燃气不会直接与水面发生作用，仅有低速空气会与水面产生微弱的作用，这一过程对发射的影响可以忽略不计。

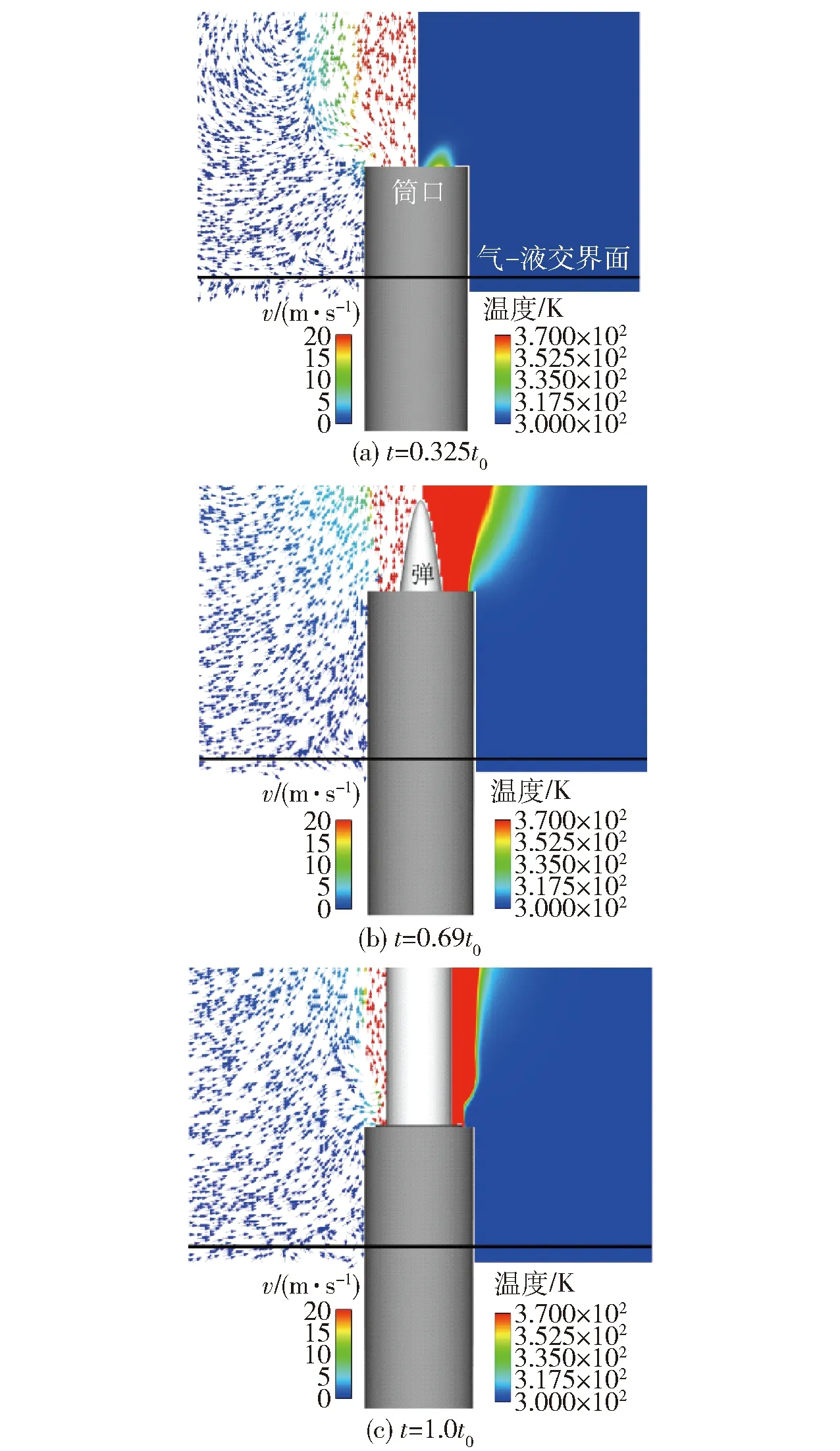
图13 筒口流动速度矢量图与温度云图Fig.13 Vector diagrams and temperature contours near the canister lip on water-surface

3.3 出水速度对内弹道的影响

由于发射筒受到燃气的减速作用，当发射筒的出水速度不足时，发射筒的筒口将没入水下，水将倾入发射筒内，在高温燃气作用下，水将发生相变，消耗燃气大量的能量，大大降低弹的出筒速度，甚至会影响弹的发射安全性，这种情况将视为发射失败。由31节的内弹道性能分析可知，水面发射弹体的出筒速度增量要小于地面发射的出筒速度增量，但由于水面发射中发射筒有出水速度，水面发射弹体的出筒速度要快于地面发射的出筒速度。为了使发射安全，以及弹体的出筒速度不小于地面发射的出筒速度，水面发射筒的出水速度需要满足一定的条件，因此有必要分析出水速度对水面发射内弹道的影响。

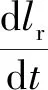
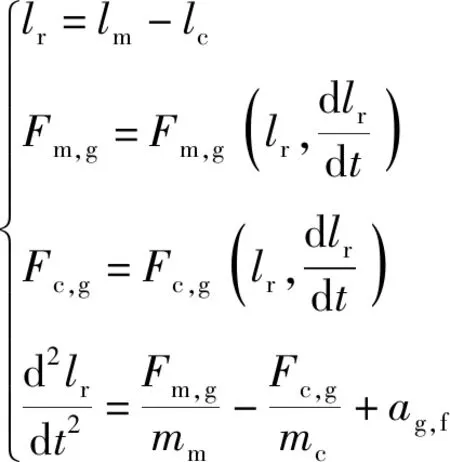
(10)

式中：为导弹的位移；为筒的位移；为重力和摩擦力提供的加速度。从(10)式可知，弹筒的相对位移与弹筒的出水速度无关，而弹、筒受到的燃气力仅与弹筒相对位移以及其相对速度有关，因此燃气力- 相对位移变化曲线不会随出水速度发生改变。

当考虑水对筒的作用力、弹受到的空气阻力作用时，二者可以近似表达为

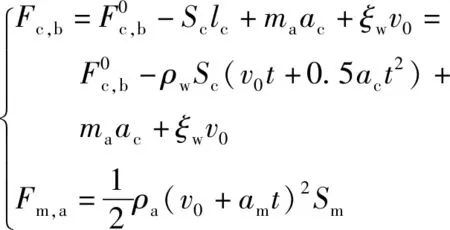
(11)

Δ=((-)+05(-))+
(-)+(-)

(12)

式中：、分别为弹体速度、下筒的加速度。

从(12)式可知，由于发射筒出水速度有限，当前条件下，其不大于10 m/s，因此速度项产生的水对筒的作用力差值与燃气力相比远远较小。发射筒的加速度主要由燃气力贡献，对于不同的出水速度，发射筒的加速度几乎相同。

3种不同出水速度的弹体速度曲线如图14所示，这3种出水速度分别为08、以及12，弹出筒时刻，发射筒的筒口均未没入水下。从图14中可以看出，不同出水速度的弹体速度曲线几乎为同一曲线的平移曲线。这与上述理论分析一致，出水速度在一定范围内，弹体的出筒速度增量几乎不随出水速度改变而改变，弹体的出筒速度为弹体出筒速度增量与出水速度的叠加。由于弹体的出筒速度增量不随出水速度发生改变，对于不同的出水速度，弹射用时、弹体受到的最大载荷等几乎一致，水面发射与地面发射相比较分析的主要结论几乎不随出水速度改变而改变。根据线性叠加原理可知，水面发射弹体出筒速度不低于地面发射的出筒速度，出水速度需大于0485，而水不进入发射筒内，出水速度需大于075。因此，在发射安全条件下，水面发射弹体的出筒速度一定大于地面发射的出筒速度。

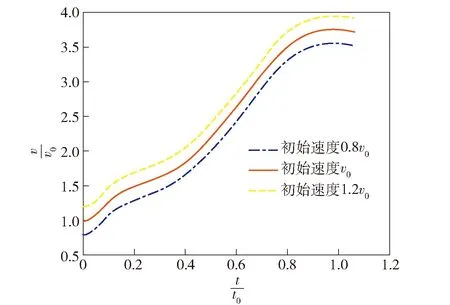
图14 不同出水速度的弹体速度曲线Fig.14 Velocity curves of projetile at different initial velocities

4 结论

本文提出一种新型发射方式即水面发射筒弹射发射方式，具有耗能少，隐蔽性强等优点，在理论上，本文是首次对弹射内弹道涉及发射平台浮动与燃气泄漏问题进行了深入研究。得出主要结论如下：

1)水面发射和地面发射具有近似的流动状态，但水面发射低压室的膨胀速度要快于地面发射的膨胀速度，主要原因是水面发射时弹筒相对速度更大。水面发射弹体的出筒速度增量小于地面发射的出筒速度增量，但由于水面发射筒有出水速度，水面发射弹体的出筒速度反而大于地面发射的出筒速度，而且水面发射弹体受到的最大载荷仅为地面发射的80，水面发射出筒用时仅为地面发射的86。

2)水面发射过程中，在给定出水速度下，燃气流出筒口时筒口已远离气液交界面，燃气不会直接与水面发生作用，仅有少量的低速空气会与水面产生微弱的作用，这一过程对发射的影响可以忽略不计。

3)在筒口不没入水时，与筒受到的燃气力相比，不同出水速度下水对筒的作用力相差较小，筒受到的加速度几乎相同，使得弹体的出筒速度增量不随出水速度改变而改变，弹体的出筒速度为弹体出筒速度增量与出水速度的叠加。因此，在安全发射条件下，水面发射与地面发射相比较分析的主要结论几乎不随出水速度改变而改变，水面发射弹体出筒速度一定大于地面发射的出筒速度。