火炮俯仰电液伺服系统速度非线性抑制技术研究
代普,潘军,马晴,刘妙
(1.西北机电工程研究所,陕西 咸阳 712099;2.咸阳师范学院,陕西 咸阳 712099)
0 引言
火炮伺服系统是火炮武器的重要组成部分,其作用是实现火炮武器的快速自动瞄准。电液伺服系统因功率密度大、响应快,在火炮伺服系统尤其是火炮俯仰伺服系统中有着广泛的应用。
火炮俯仰电液伺服系统采用液压缸作为执行机构带动俯仰部分运动,液压缸底部铰接于车体,顶部铰接于俯仰体,通过液压缸的伸缩推动俯仰体绕耳轴(俯仰部分的旋转中心)进行上下俯仰运动。鉴于这种结构,当液压缸在液压泵带动下匀速运动时,液压缸的伸缩杆也将做匀速运动,电液伺服系统输入的速度信号和液压缸的伸缩速度呈线性关系。但是,由于液压缸和俯仰体呈三角形布置,导致液压缸以固定速度伸缩时,耳轴的旋转速度会随着高低俯仰角的不同而发生变化,进一步导致电液伺服系统的给定速度和耳轴的实际运动速度呈非线性关系。由于这种非线性关系的存在,伺服系统在进行定位控制时,不同俯仰角度区间的等幅调转时间不等;在进行跟踪控制时,跟踪精度较低。
针对这一问题,目前国内外普遍采用的解决方案是引入位置主令的前馈控制或采用效果更好的位置调节器,这些方法均不能从根本上解决系统的速度非线性问题,一方面对系统动态跟踪性能的改善作用有限,另一方面对于不同俯仰角度区间等幅调转时间不等的问题毫无效果。本文通过分析火炮俯仰电液伺服系统的运动机理,建立俯仰伺服系统运动的数学模型,剖析系统的速度非线性特性,揭示系统非线性运动规律,提出一种基于非线性观测及非线性补偿的俯仰电液伺服系统速度非线性抑制方法,改善了系统的控制特性,通过仿真及试验表明,该方法对俯仰电液伺服系统的速度非线性具有较好的抑制效果。
1 火炮俯仰电液伺服系统组成及工作原理
1.1 液压系统组成及工作原理
液压系统的工作原理如图1所示,液压系统采用泵控缸闭式系统,主要由油箱、伺服泵、控制阀组、液压缸、锁紧阀组等组成。油箱用于提供系统所需油源;伺服泵是液压系统的动力源,可根据电信号的大小和极性控制伺服泵输出压力油流量的大小和流动方向,伺服泵具有两个出油口,通过控制阀组、锁紧阀组分别与液压缸的上腔和下腔相连;控制阀组用于控制液压系统工作压力和控制压力的开启和关断;液压缸是电液伺服系统的执行元件,液压缸的一端通过支架铰接在底盘上,另一端铰接在俯仰体上,用于控制俯仰体绕耳轴的俯仰运动;锁紧阀组用于实现液压系统运动到位后的锁定。

图1 液压系统原理图Fig.1 Schematic diagram of hydraulic system
液压系统工作时,伺服泵输入轴以恒转速旋转,通过伺服阀控制伺服泵输出流量的大小和方向,来控制液压缸的运动速度和运动方向。当液压缸A腔注油时,液压缸伸长,俯仰体向上运动;当液压缸B腔注油时,液压缸缩短,俯仰体向下运动,C腔为平衡腔。
1.2 俯仰电液伺服系统的工作原理
电液伺服系统由伺服控制器、液压系统及测角装置组成。伺服控制器包含位置控制器和伺服驱动器,位置控制器用以完成伺服系统的位置控制,位置控制器以数字信号处理器TMS320F28335为主控单元,通过CAN总线接收火控系统的位置主令,通过轴角数字转换模块采集测角装置的反馈角度,实现位置环的控制量计算;伺服驱动器用以接收位置控制器的输出速度信号,完成速度(流量)调节,然后输出差动电流信号,用于驱动伺服泵上的电液伺服阀,进一步控制伺服泵输出液压油流量的大小和方向,推动液压缸伸缩,带动俯仰体实现俯仰运动。俯仰电液伺服系统的工作原理如图2所示。

图2 俯仰电液伺服系统原理图Fig.2 Schematic diagram of pitching electro hydraulic servo system
2 俯仰运动的数学模型
2.1 俯仰运动的数学模型
电液伺服系统俯仰运动示意图如图3所示。图3中,点为俯仰体旋转中心(又称为耳轴),点为液压缸缸体下端,点为液压缸缸体上端,点为液压缸伸缩杆上端,点随液压缸的伸缩,其位置发生变化,当液压缸收缩至俯仰体和安装面平行位置时,液压缸上端在位置,当液压缸伸出最大长度时,液压缸上端在位置,当液压缸伸出在中间位置时,对应液压缸上端分别在、位置。当俯仰体运动时,点和点固定,点和点随液压缸的伸缩而运动,也即△的边固定,边绕点旋转,的长度随液压缸伸缩而发生变化,液压缸最短时其上端点为,液压缸伸出过程的两点依次为和,液压缸最长时其上端点为。假设旋转至与安装平面平行时,∠=,旋转至最大角度时,∠=,则∠∈[,],俯仰体和安装平面的夹角为,为俯仰体实际俯仰角,=∠-。令=,=,=,假设液压缸向上运动过程中,时刻液压缸长度为,俯仰体在位置,俯仰体角度为∠=;时刻液压缸长度为,俯仰体在位置,俯仰体角度为+Δ;从时刻到时刻,液压缸的长度增量为,俯仰体旋转过的角度为Δ,圆弧长度为,点为点到直线的垂足。

图3 电液伺服系统俯仰运动示意图Fig.3 Pitching motion diagram of electro hydraulic servo system
根据余弦定理易知:
=+-2cos
(1)
令=,假设液压缸以恒定速度伸出,伸出时间为,=+,则
(+)=+-2cos
(2)

(3)
因此俯仰系统的俯仰角为
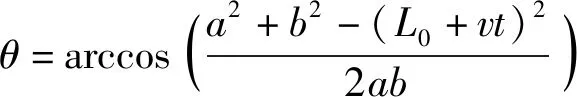
(4)
对(1)式求导,得俯仰系统的角速率为
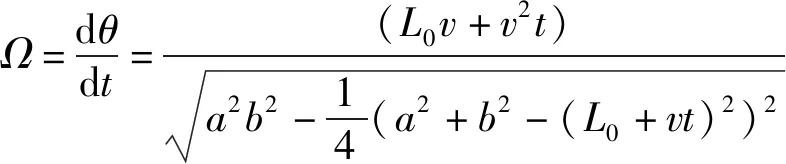
(5)
由(1)式知:

(6)
将(6)式代入(5)式,得

(7)
(6)式即为当液压缸以恒定速度伸出时俯仰角速率和俯仰位置角的函数关系,易知当液压缸伸缩速度为定值时,俯仰体的俯仰角速率和俯仰位置角呈非线性关系。

=()
(8)
2.2 速比函数的值域
参见图3,令===1,则=Δ×=Δ×1=Δ,则
从时刻到时刻,俯仰体角速度的平均值为

(9)
从时刻到时刻,液压缸线速度的平均值为
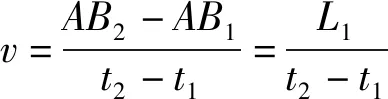
(10)
从时刻到时刻,俯仰体角速度的平均值和液压缸线速度的平均值的比值称为平均速比,则平均速比为
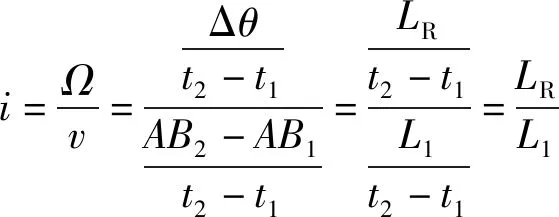
(11)
()为俯仰体在角度时的及时速比,则及时速比()为
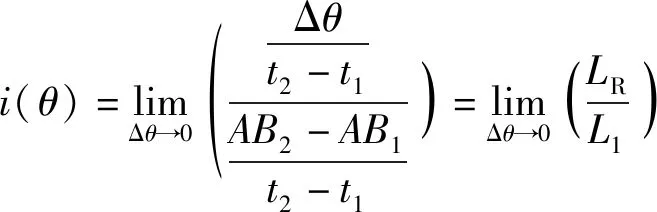
(12)
近似为直角三角形,∠=90°,易知,=×cos∠,因此在任何情况下均有≥,当且仅当∠=90°时,即俯仰体和液压缸垂直时=,()=1,其他任何角度均有()>1。
假设=×(≥1),令()=1对应的角度=cos(1)。
假设=15°,∈[0°,70°],则∈[15°,85°],分别令取值为10、15、20、30,()函数曲线如图4所示。

图4 不同n值的i(θ)曲线图Fig.4 i(θ) curve of different n values
由图4可知:()随俯仰角变化而变化,当取值为1时()取值变化范围最小;当取值增大时,()变化范围增大;在取不同值时,均有()≥1,()=1对应的角度随值的不同而出现在不同的角度。
3 系统动态结构及速度非线性抑制方法

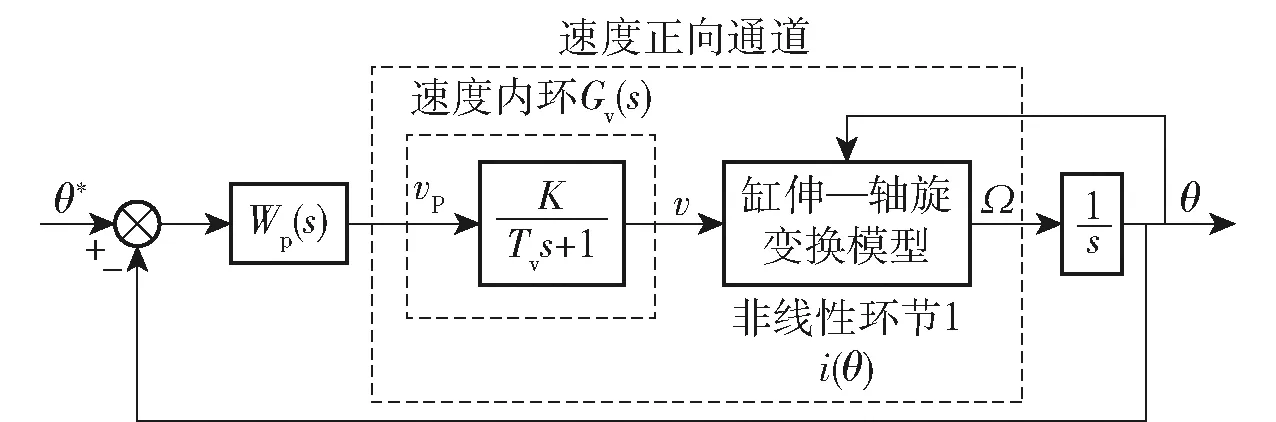
图5 系统动态结构图Fig.5 System dynamic structure diagram
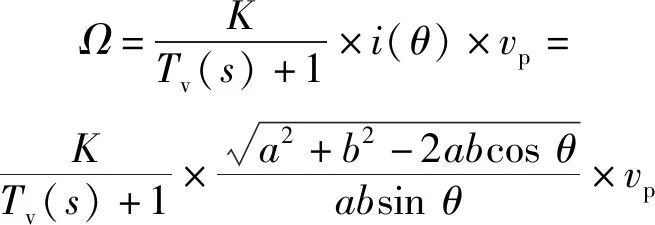
(13)
易知,和呈非线性。
为对()的非线特性进行抑制,在位置调节器后端引入非线性环节2,称为非线性抑制环节(),非线性抑制环节()的传函为
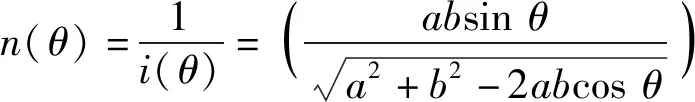
(14)
引入非线性环节2后系统动态结构图如图6所示,为速度非线性抑制环节输出的速度主令。由图6可知,此时系统俯仰速度为

图6 系统速度非线性抑制动态结构图Fig.6 Dynamic structure of nonlinear speed suppression of the system
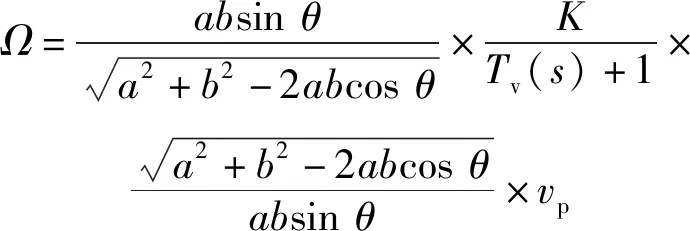
(15)
因此,

(16)
引入非线性抑制环节2后,速度系统等效速比为1。假如系统速比()<1,则量值为1的速比相当于对系统饱和速度主令所对应的俯仰速度进行了放大,而对于固定的缸伸速度和值,系统实际的最大俯仰速度不可能放大而只可能减小,即只有非线性抑制前速度系统的速比()≥1,才可能通过此方法实现系统速度的线性化。由图4可知,在取不同值时,均有()≥1,故该方法是可行的。
采用该方法后,系统速比()≥1的部分被钳位,使其恒取最小值1,即进行速度非线性抑制后,饱和速度主令在()=1时所对应的俯仰速度,是非线性抑制前系统饱和速度主令所对应的最小俯仰速度,也将是非线性抑制后系统饱和速度主令所对应的最大俯仰速度。
4 速度非线性抑制仿真系统建模
伺服系统主要参数:位置调节器输出也即速度主令为-10~10 V,液压系统时间常数0.105 s,液压系统增益为0.025 1,也就是1 V的速度主令对应的液压缸伸出速度为0.025 1 m/s。
电液伺服系统仿真图如图7所示。图7中,Step为阶跃信源,Ramp斜坡信源,开关Switch1用于信源的切换,模块Subsytem1为位置调节器,模块Subsytem2为前馈调节器,add为加法器,Satu为位置环输出饱和环节。Transfer为液压系统等效的1阶惯性环节,Integr为积分环节。模块Zbbh1为非线性环节1,即缸伸- 轴旋非线性模型,其输入为缸伸速度和俯仰角,输出为俯仰体俯仰角速度,模块Zbbh2为非线性环节2,也即人为引入的非线性环节,其输入为俯仰角和速度主令给定,输出为非线性抑制后实际的速度给定,Gain为比例环节,用于单位变换,系统输出俯仰角为(mrad),Gain的增益为180314×1666,为俯仰三角的最小俯仰角,其值为15°。开关Switch2用于非线性环节2的引入和去除,Switch2向上切换时,非线性抑制环节2引入,开关Switch2向下切换时,非线性抑制环节2去除,加入开关Switch2的目的是便于对比引入非线性环节2和去除非线性环节2时系统的控制效果。
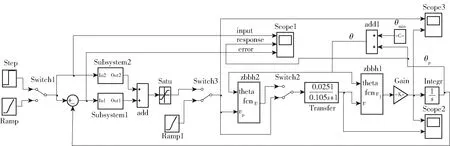
图7 非线性抑制系统仿真图Fig.7 Simulation diagram of nonlinear suppression system
5 仿真及应用效果
5.1 速度非线性抑制效果
在俯仰伺服系统工作过程中,液压缸的伸出速度是随速度主令的变化而变化的,为了对比采用速度非线性抑制方法前后,系统速度环节对于不同速度主令的非线性抑制情况,将系统位置环输出断开,并通过斜坡信源ramp1加入斜坡速度主令,通过Scope3观察系统在无非线性抑制和有非线性抑制两种情况下系统的俯仰速度。
图8所示为ramp1加入的斜坡速度主令。

图8 速度主令曲线Fig.8 Speed order curve
图9所示为无速度非线性抑制系统的俯仰速度。由图9可知,对于3种斜率的速度输入,俯仰速度均呈非线性。

图9 无非线性抑制俯仰速度曲线Fig.9 No nonlinear suppression pitching curve
图10所示为有速度非线性抑制系统的俯仰速度。由图10可知,对于3种斜率的速度输入,输出俯仰速度均呈线性。
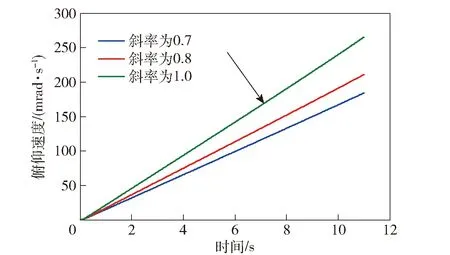
图10 有非线性抑制俯仰速度曲线Fig.10 Nonlinear suppression pitching curve
5.2 系统控制效果
图11所示为系统调转曲线,图11(a)为无速度非线性抑制环节情况下的曲线,图11(b)为有速度非线性抑制环节情况的曲线(系统的位置主令为图3中的,=+)。在无速度非线性抑制环节的情况下,系统从0 mrad向917 mrad调转时,系统可实现准确定位,定位误差小于0.2 mrad;在加入速度非线性抑制环节的情况下,系统从0 mrad向917 mrad调转时,系统可实现准确定位,定位误差小于0.2 mrad。表明有无速度非线性抑制,对系统定位精度基本无影响。
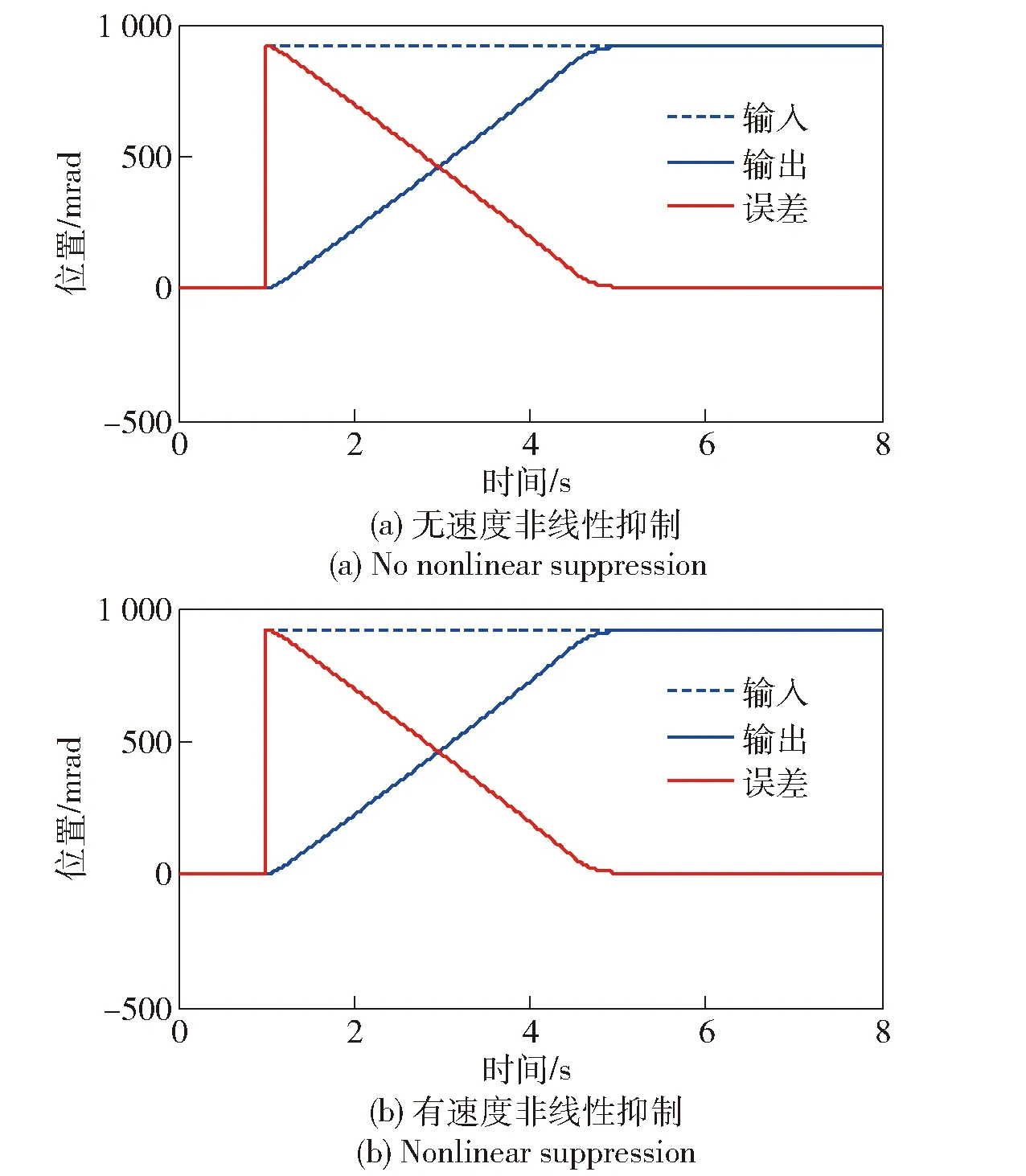
图11 系统调转曲线Fig.11 Transfering position curve
图12所示为系统调转过程中的缸伸速度曲线,图12(a)为无速度非线性抑制环节情况下的缸速度曲线,图12(b)为有速度非线性抑制环节情况的缸速度曲线。系统从0 mrad向917 mrad调转过程中,在无速度非线性抑制环节的情况下,系统缸速度速度中间段恒定为0.28 m/s,在有速度非线性抑制环节的情况下,系统缸伸速度中间段从0.29 m/s向0.26 m/s变化。
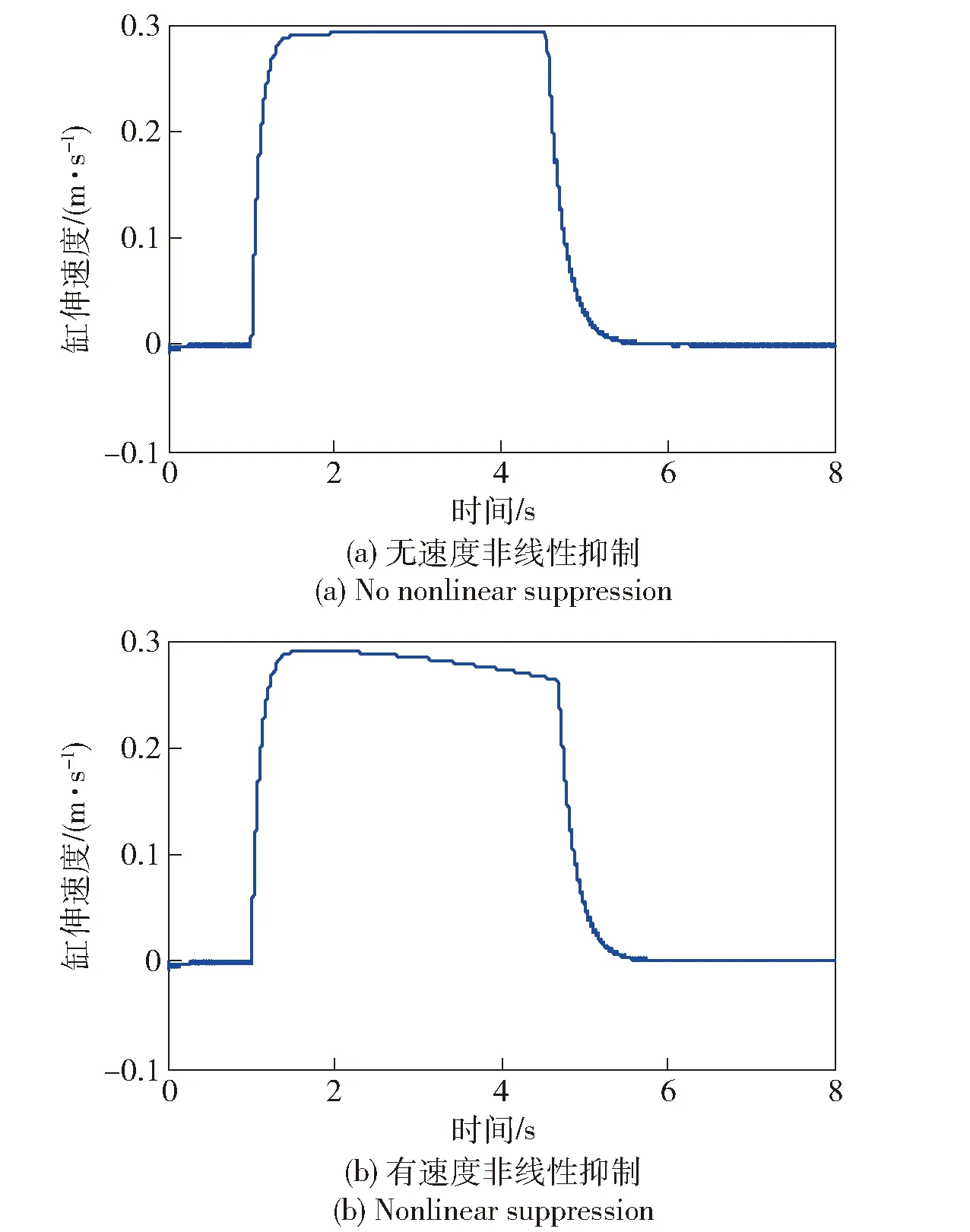
图12 调转过程中的缸伸速度曲线Fig.12 Cylinder speed curve while transferring
图13所示为系统调转过程中的轴旋速度曲线,也就是俯仰体的旋转速度曲线,图13(a)为无速度非线性抑制环节情况下的轴旋速度曲线,图13(b)为有速度非线性抑制环节情况的轴旋速度曲线。系统从0 mrad向917 mrad调转过程中,在无速度非线性抑制环节的情况下,系统轴旋速度中间段从240 mrad/s到270 mrad/s变化,在有速度非线性抑制环节的情况下,系统轴旋速度中间段恒定为240 mrad/s。

图13 调转过程中的俯仰速度曲线Fig.13 System rotating speed curve while transferring
综合图12及图13可知:系统从0 mrad向917 mrad调转过程中,未加入速度非线性抑制环节时,缸伸速度中间段恒定,轴旋速度中间段数值变化,表明系统的最大俯仰速度是随俯仰角发生变化的,系统表现出速度非线性特性;加入速度非线性抑制环节时,缸伸速度中间段变化,轴旋速度中间段度恒定。系统大调转的中间段速度因饱和而不变,即在系统速度主令恒定时,俯仰速度也是恒定的,即速度环输入输出呈线性特性,系统速度非线性特性得以完全抑制。
图14所示为系统不同角度等幅值调转的速度时间曲线,图14(a)为无速度非线性抑制环节的情况下从0 mrad到600 mrad、从600 mrad到1 200 mrad调转时间曲线,图14(b)为有速度非线性抑制环节的情况下从0 mrad到600 mrad、从600 mrad到1 200 mrad调转时间曲线。在无速度抑制环节情况下,系统从0 mrad到600 mrad调转时间为3.2 s,从600 mrad到1 200 mrad调转时间为3.0 s,不同区间的等幅调转时间不等;在加入速度抑制环节情况下,系统从0 mrad到600 mrad调转时间为3.2 s,从600 mrad到1 200 mrad调转时间为3.2 s,不同区间的等幅调转时间相等,可见,在引入速度环非线性抑制后,系统在各个角度区间的等幅调转时间相等。

图14 不同角度区间等幅值调转的速度- 时间曲线Fig.14 Speed-time curve of equal amplitude rotation at different angles range
图15所示为系统等速跟踪的位置响应曲线,图16所示为系统等速跟踪的误差响应曲线。由图15和图16可知,在无速度非线性抑制环节情况下,系统加入150 mrad/s的等速主令,系统达到稳定跟踪的时间1.7 s,动态过程误差13 mrad,稳定跟踪误差0.8 mrad;在加入速度非线性抑制环节情况下,系统加入150 mrad/s的等速主令,系统达到稳定跟踪的时间1.0 s,动态过程误差5 mrad,稳定跟踪误差0.2 mrad。可见,在加入速度非线性抑制环节的情况下,系统的等速跟踪能力得以较好的提升,动态过程缩短,稳态跟踪精度大幅提高。
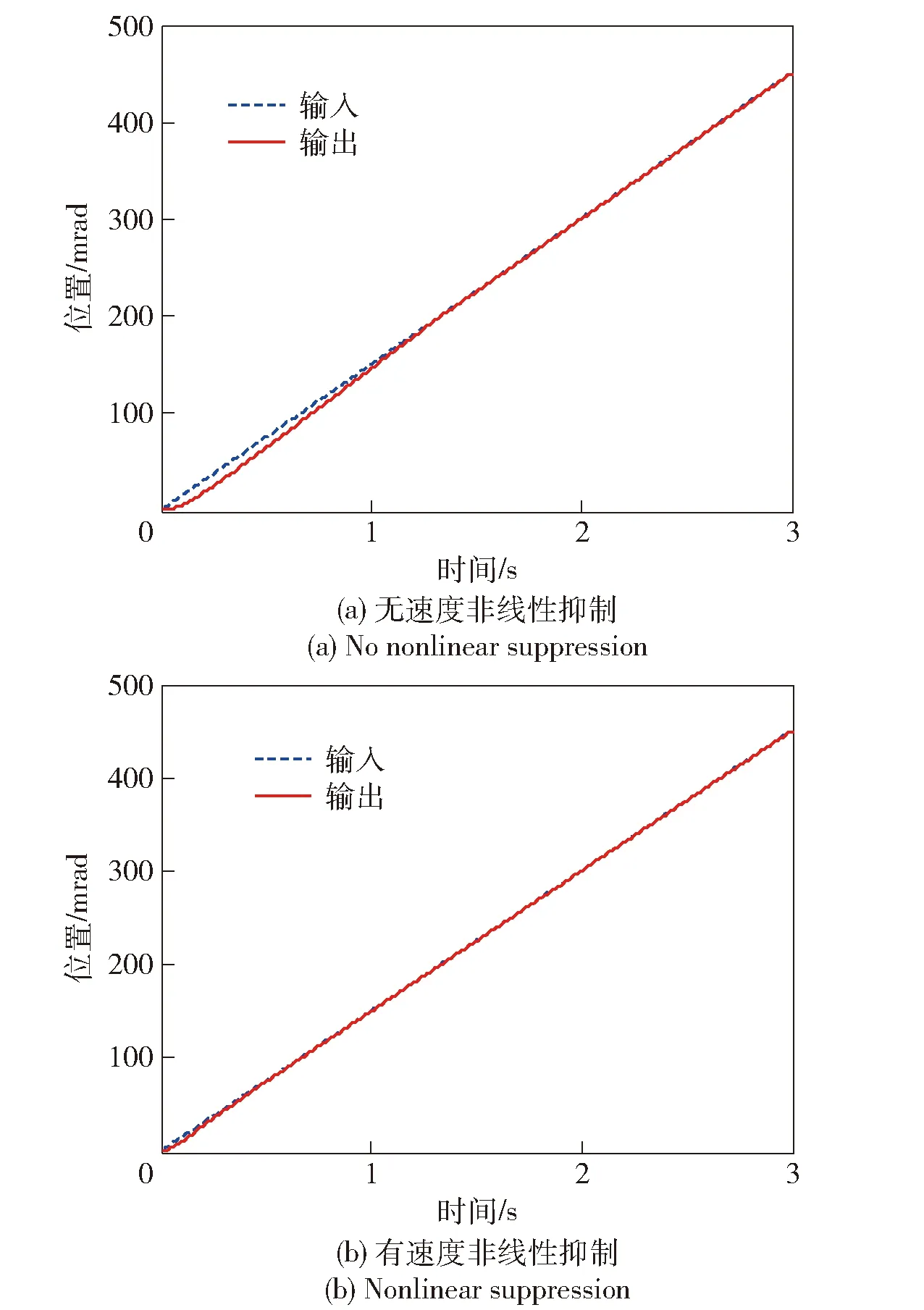
图15 系统等速跟踪位置曲线Fig.15 Slope tracking curve
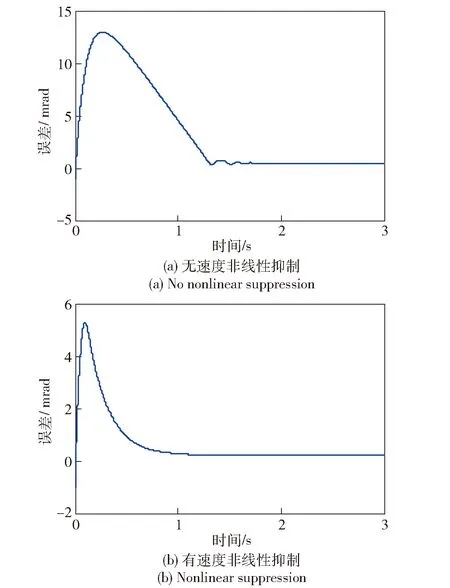
图16 系统等速跟踪误差曲线Fig.16 Slope tracking error curve
5.3 样机应用效果
将速度非线性抑制方法应用于某火炮俯仰电液伺服系统:在未采用速度非线性抑制方法时,系统100 mrad/s等速跟踪稳态误差为2.1 mrad,采用速度非线性抑制方法后,系统等速跟踪稳态误差0.4 mrad;在未采用速度非线性抑制方法时,系统150 mrad/s等速跟踪稳态误差为2.5 mrad,采用速度非线性抑制方法后,系统等速跟踪稳态误差0.5 mrad。
在未采用速度非线性抑制方法时,系统0~500 mrad调转时间、500~1 000 mrad调转时间分别为2.8 s、2.6 s,采用速度非线性抑制方法后,系统0~500 mrad调转时间、500~1 000 mrad调转时间均为2.8 s。
6 结论
本文通过对火炮俯仰电液伺服系统的运动机理进行分析,建立了系统速度传递的数学模型,剖析了俯仰系统速度非线性随角度的变化规律,在此基础上提出了基于非线性补偿的系统速度非线性抑制方法,通过仿真和试验表明,该方法对火炮俯仰电液伺服系统速度的非线性抑制具有较好的效果。得出主要结论如下:
1)火炮俯仰电液伺服系统采用速度非线性抑制方法解决了俯仰电液系统速度非线性问题,实现了俯仰系统速度控制线性化。
2)火炮俯仰电液伺服系统采用速度非线性抑制方法解决了不同俯仰位置区间的等幅调转时间不等的问题。
3)火炮俯仰电液伺服系统采用速度非线性抑制方法极大提高了系统的动态跟踪性能。

