爆炸载荷下脆性颗粒体系破碎特性的数值研究

张传山， 冯 春， 薛 琨*

(1.北京理工大学 爆炸科学与技术国家重点试验室，北京 100081；2.中国科学院 力学研究所 流固耦合系统力学重点试验室，北京 100190)

1 引 言

脆性颗粒体系在爆炸载荷冲击作用下的破碎现象广泛存在于采矿爆破、防护设计和地震工程等工程应用中[1,2]。研究脆性颗粒材料在爆炸载荷下的破碎特性，特别是破碎体积分数随震源距离的变化，对于预测爆炸波在颗粒散体中的传播衰减规律、爆源能量的耗散模式和效率、预测颗粒材料的吸能防爆特性以及爆破震源的优化设计具有重要的价值[3,4]。

由大量离散颗粒个体构成的颗粒材料在承受外界载荷时会在体系内部形成各向异性的力链网络结构，力链网络上的少量颗粒承担了大部分力，使得应力分布呈现强烈的空间非均匀性和方向性[1,5]。爆炸载荷加载下颗粒体系中应力空间分布的非均匀性、瞬态性和颗粒内部的非平衡应力状态使得颗粒体系的破碎表现出比准静态和动态压缩加载下更为复杂的行为。目前对于颗粒破碎的研究主要针对准静态和动态压缩加载下处于力平衡状态下的颗粒，主要集中在理论模型建立和试验技术探索方面。文献[6-9]开展了系统的玻璃珠单体和石英砂体系分离式霍普金森压杆(Split Hopkinson Pressure Bar)试验，提出了基于破坏模式的与应变率相关的颗粒破碎强度双Weibull分布，分析了颗粒的破碎模式、碎片形貌以及碎块的统计特征与加载应变率的依赖关系，揭示了冲击压缩过程中颗粒破碎程度对宏观体系动态响应的影响，探讨了影响脆性颗粒破碎和颗粒介质中应力波衰减的因素，并基于离散元方法构建了多尺度模型用于动态加载研究。

与准静态和动态加载中主导的拉伸、剪切和压剪破坏机制不同，破坏波(Failure waves)是强脉冲爆炸波加载下脆性材料，特别是玻璃的主导破坏模式。目前，尚未有统一的理论模型能准确解释破坏波的产生、传播及与材料相互作用的物理力学机理[10,11]。如何考虑爆炸波加载下颗粒个体内部破坏波复杂的传播过程，进而给出颗粒的破碎准则，是揭示颗粒体系整体破碎行为的关键问题。

目前颗粒材料的爆炸加载破碎试验只能得到颗粒体系的宏观破碎特性，如不同材料和当量比(颗粒体系与炸药的质量比)下颗粒破碎体积分数、破碎指数和分型维度等参数，难以捕捉颗粒尺度上的应力传播和破碎行为。而能够解析颗粒尺度动力学行为的离散元方法已经广泛用于模拟不同载荷路径下颗粒体系内部的应力分布，并预测颗粒的破碎程度。因此，本文将采用宏观试验与数值模拟相结合的手段，用试验得到的颗粒体系宏观破碎特性校验数值模拟的结果，然后从颗粒尺度的破碎行为出发解释和预测宏观破碎特性。

2 试验方法和结果分析

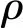
试验前将装填好的玻璃球悬挂在距离地面 1.8 m 的位置处。为了便于收集破碎后的颗粒，在以玻璃球为中心半径1.94 m的圆周上树立10块高2.4 m的挡板。试验场地布置如图1(c)所示。爆炸波加速的颗粒碎片在撞上刚性表面后往往会发生二次破碎，为了尽可能避免二次破碎，地面和挡板内侧均覆盖有5 mm厚的软橡胶层。通过增大玻璃球壳的直径，装药当量比从10.2增加到424，变化了两个数量级。所有工况均进行5次以上的试验，每次试验后回收到的颗粒质量为初始装填质量的50%～90%。

图1 球形装药结构、试件实物和回收装置

采用基于动态图像分析技术的颗粒粒径分析仪CAMSIZER®测量了试验后回收的颗粒碎片(包括破碎和完整的颗粒)的粒径分布，ftested(dp)如图2所示。通过试验前后粒径分布的变化可以获得颗粒体系的破碎体积分数Φ。图3为Φ随M/C的变化曲线，呈现出明显的指数衰减规律,即

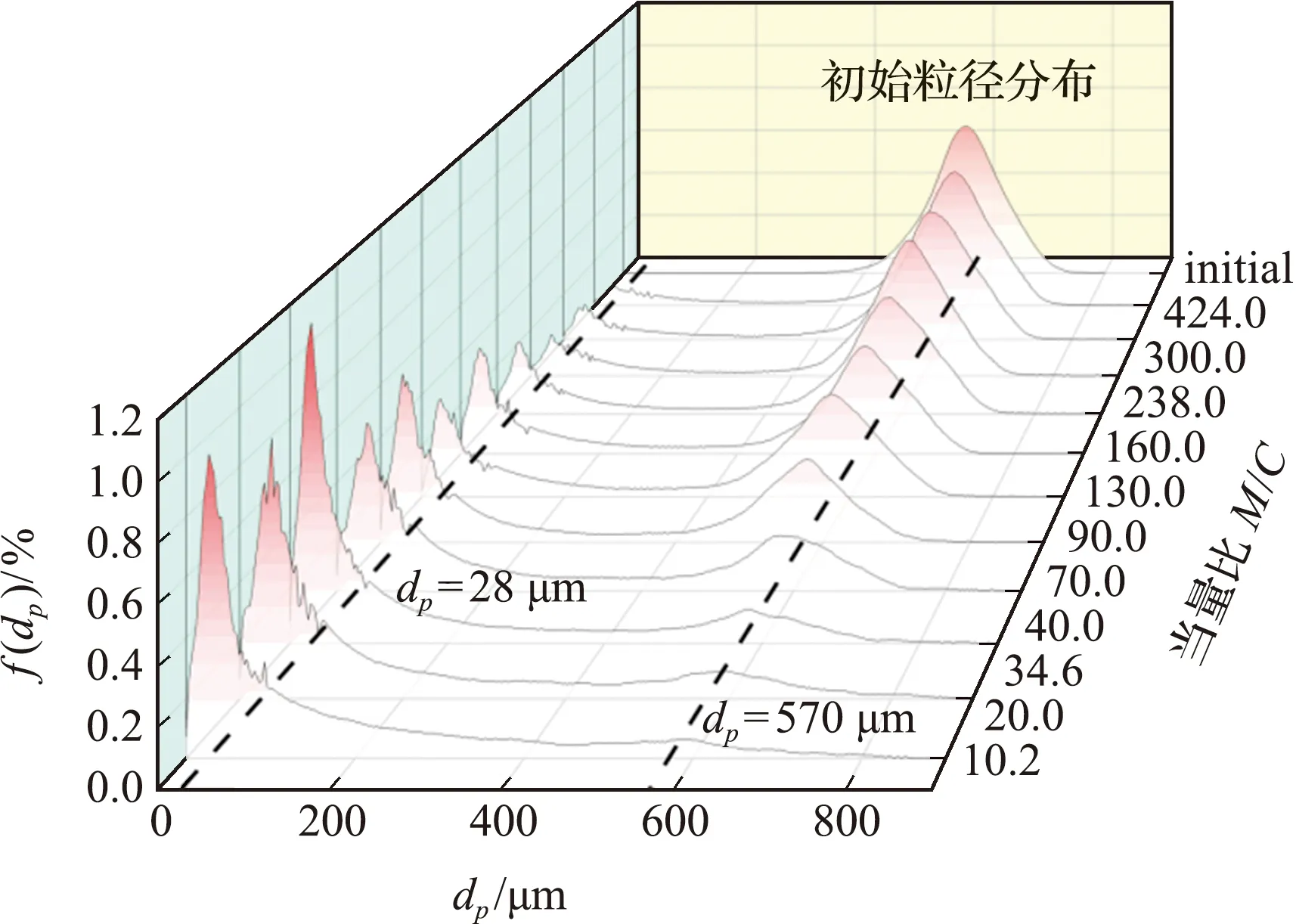
图2 试验后回收的颗粒碎片粒径分布

图3 完全破碎颗粒的体积分数Φfrag随当量比M/C的变化

(1)

显然，Φ随M/C的增加而迅速衰减的现象与爆炸波在颗粒体系的传播衰减密切相关。

3 数值方法

采用拉格朗日有限元模拟炸药的起爆和爆轰产物气体的膨胀过程。未反应的炸药单元和爆轰产物气体的状态方程分别采用冲击波状态方程和JWL状态方程描述。炸药点火模型，状态方程模型参数和有限单元的变形迭代算法详见文献[12]。离散颗粒的运动遵循动量和角动量守恒,与炸药(爆轰产物气体)无直接接触的颗粒所受的合力包含接触颗粒之间的法向力和切向力。采用线性弹簧-阻尼颗粒接触模型，通过增量更新计算接触力。模拟计算的微观力学参量列入表1。离散颗粒之间、颗粒与炸药单元之间的接触检测算法详见文献[12]。

表1 数值计算中微观力学参数

该方法模拟得到的中心炸药爆炸驱动下颗粒层的飞散速度与Milne[13]给出的适用于多孔填充材料的格尼速度非常吻合，如图4所示，验证了模型及其参数的可靠性。

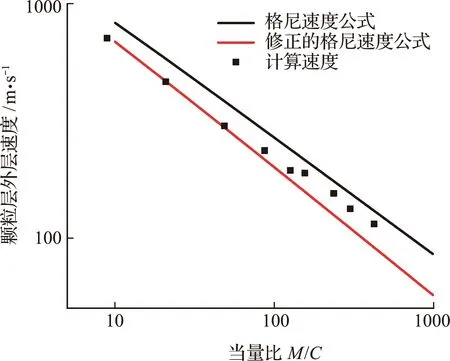
图4 最外层颗粒速度与格尼公式的对比

4 强脉冲载荷下颗粒破碎准则

4.1 破坏波模式下的颗粒破碎强度Weibull统计分布

文献常用的准则忽略了配位数对颗粒破碎的影响，在大多数情况下，选用基于颗粒的力或压力阈值作为破碎准则。本文也采用这种方法。在离散颗粒模型中，经常采用通过颗粒名义应力σi j定义的诱导应力σt来判断颗粒是否发生破碎。颗粒的名义应力σi j与其接触力的关系为

(2)

(3)

式中si j=σi j-δi j(σ11+σ22+σ33)/3为名义应力的偏应力。大量的准静态压缩试验研究表明单个颗粒的破碎强度满足Weibull统计分布，即粒径为dp的颗粒在诱导应力σt下的存活(不破碎)概率为

(4)

式中σ0为粒径为dp 0的颗粒存活(不破碎)概率为37%时对应的诱导应力，m为表征颗粒强度分散度的Weibull模量。对于文献[14]不同粒径球形玻璃珠高应变率SHPB试验的结果，本文给出dp 0=0.5 mm的玻璃珠在应变率103/s的动态加载下的Weibull强度分布参数为m=6.3,σ0=306.21 MPa。

图5显示了M/C=126的二维工况中颗粒环壳内不同震源距离R处的颗粒受到诱导应力σt的时程曲线。σt在爆炸波到达后突然起跳，此后在μs尺度上经历高频振荡衰减。直接采用式(4)会导致对于颗粒破碎体积分数的数值预测远高于试验值。

图5 M /C =126的二维工况不同震源距离R处的颗粒受到σt(包络面积为灰色)和包络面积为蓝色)的时程曲线

因此，有必要对式(4)进行修正，使其能够充分考虑爆炸载荷下颗粒应力迅速( μs量级)衰减和强振荡的特征对于颗粒破碎的影响，进而发展适应于离散元模型的强幅值短脉冲载荷下的颗粒破碎准则。考虑到破坏波导致颗粒破碎的充分条件为,在破坏波贯穿整个颗粒直径的时间(tfailuer)内，颗粒内部压缩应力不会下降到破坏波自维持的阈值(σfailure)以下，可以给出破坏波主导下颗粒破碎的一阶近似准则

(5)

(6)

进而得到修正后的颗粒破碎强度Weibull分布

(7)

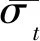
4.2 颗粒破碎判别算法

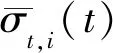
(8)

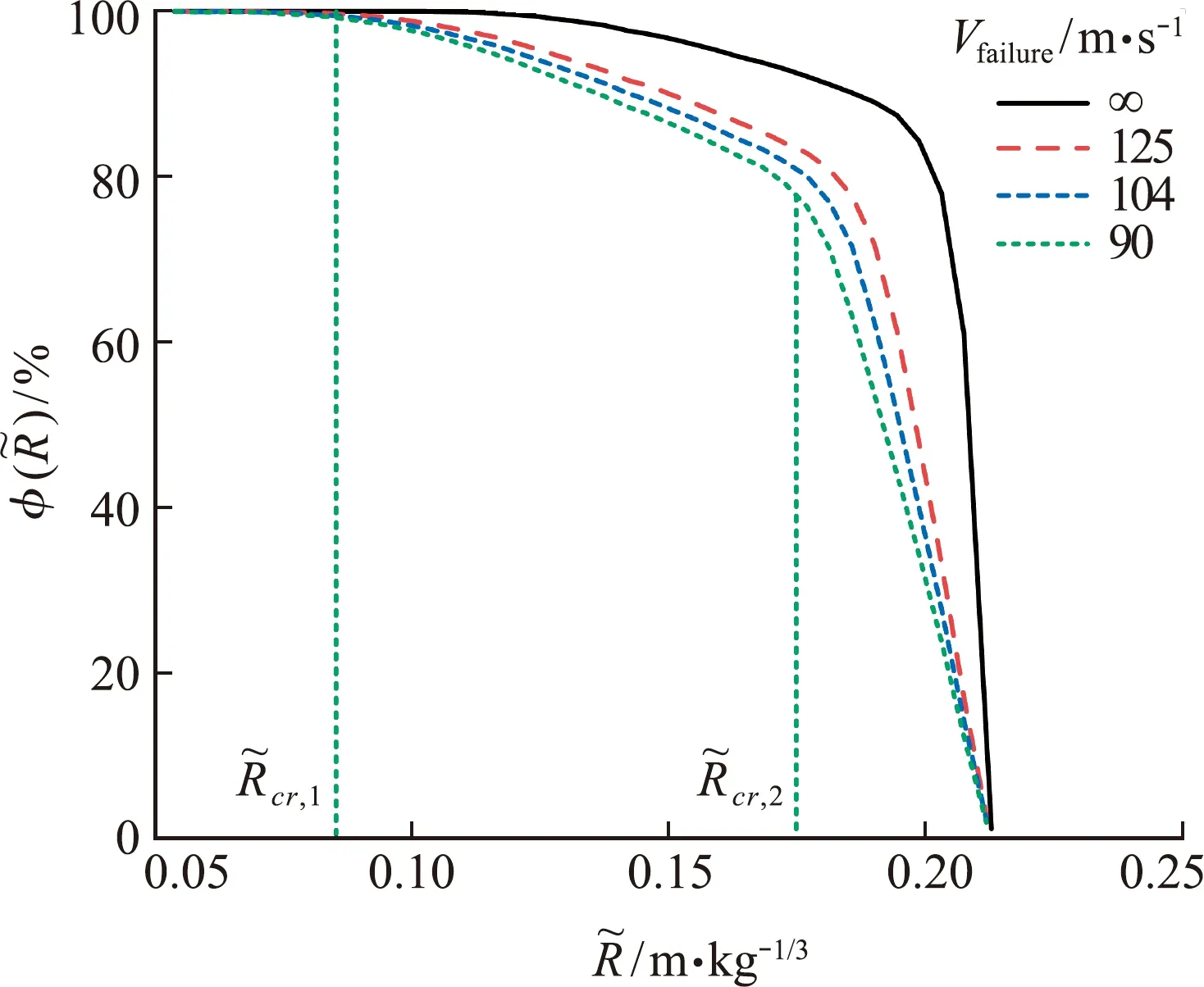
图6 不同破坏波传播速度下的破碎概率与震源比例距离的变化

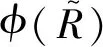
(9)

对于二维柱装药构型有

(10)

图7为模拟得到的三维颗粒球壳(M/C=66)中破碎颗粒体积分数Φnum随Vfailure的变化。Vfailure=95 m/s时，Φnum=65%，与M/C=70工况下试验得到的破碎颗粒体积分数Φexp=64%吻合程度最高，因此本文将Vfailure=95 m/s作为破坏波的特征传播速度，进而采用修正颗粒破碎强度Weibull分布(式(7))计算颗粒破碎概率。

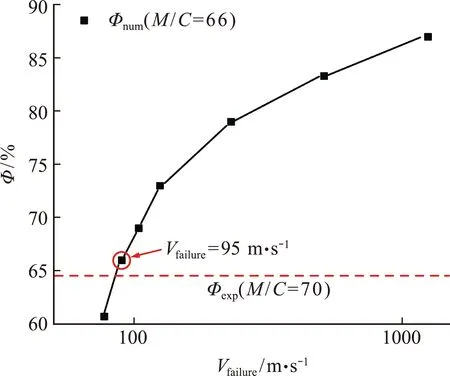
图7 三维颗粒球壳模型(M /C =66)中破碎颗粒体积分数Φ随Vfailure的变化

5 计算结果

5.1 爆炸波在颗粒层中的传播规律

图8为M/C=20.8的二维颗粒环壳在中心炸药起爆后，爆轰产物气体和颗粒环壳内压力分布的演化。爆炸波进入颗粒环壳内成为入射激IS(incident shock)，驱动颗粒环壳加速膨胀。受颗粒环内界面约束的爆轰产物气体随着内界面的向外运动迅速膨胀，内部压力显著下降，入射激波也呈高幅值短历时的三角波形。

图8 M /C =20.8的二维颗粒环壳在中心炸药起爆后的压力场的时空演化

如图9所示，颗粒压力时程曲线ΔP(t)在入射激波达到时突然起跳，此后迅速衰减。当入射激波到达颗粒环壳外界面时形成反向传播的稀疏波RW(rarefaction wave)，稀疏波路径上的压实颗粒迅速卸载，表现为图9中颗粒压力在稀疏波到达后迅速卸载到零。此后从中心反射向外传播的二次爆炸波进入颗粒环壳，形成二次压缩波SCW(secondary compression wave)。颗粒压力在二次压缩波作用下小幅起跳(图9)，但二次压缩波峰值超压比入射波小一个数量级，因此颗粒破碎仅发生在入射波作用阶段。

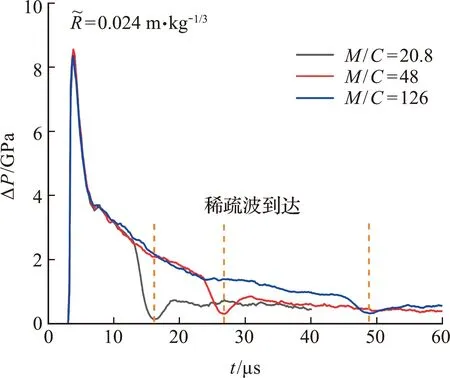
图9 典型工况中处于同样震源比例距离的颗粒受到的压力时程曲线

图10 最大平均诱导应力随震源比例距离的变化

(11)

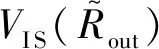
5.2 应力场分布

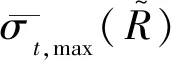
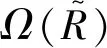
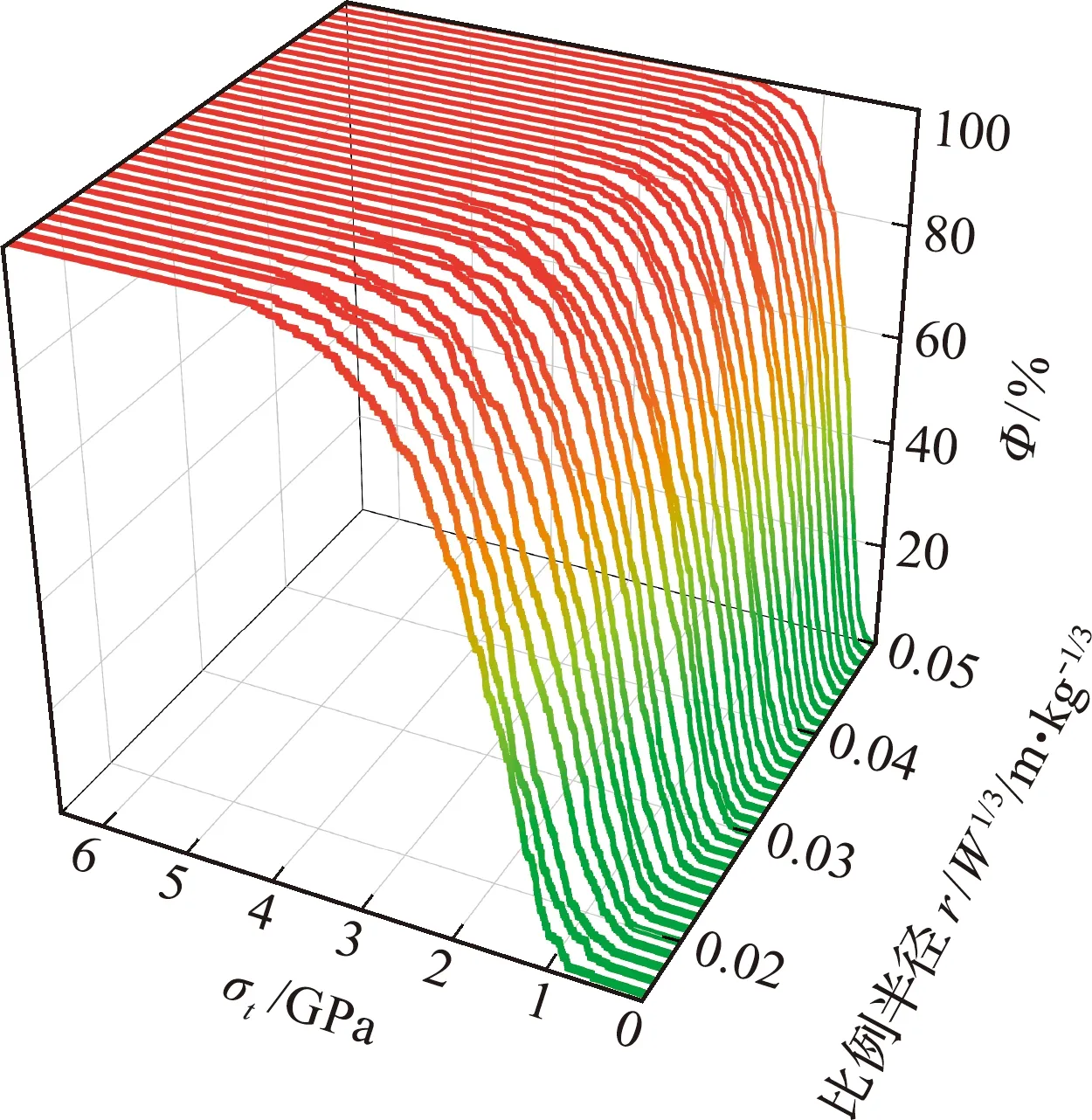
图11 不同环形区域内的累积概率密度(M /C =20.8)

(12)

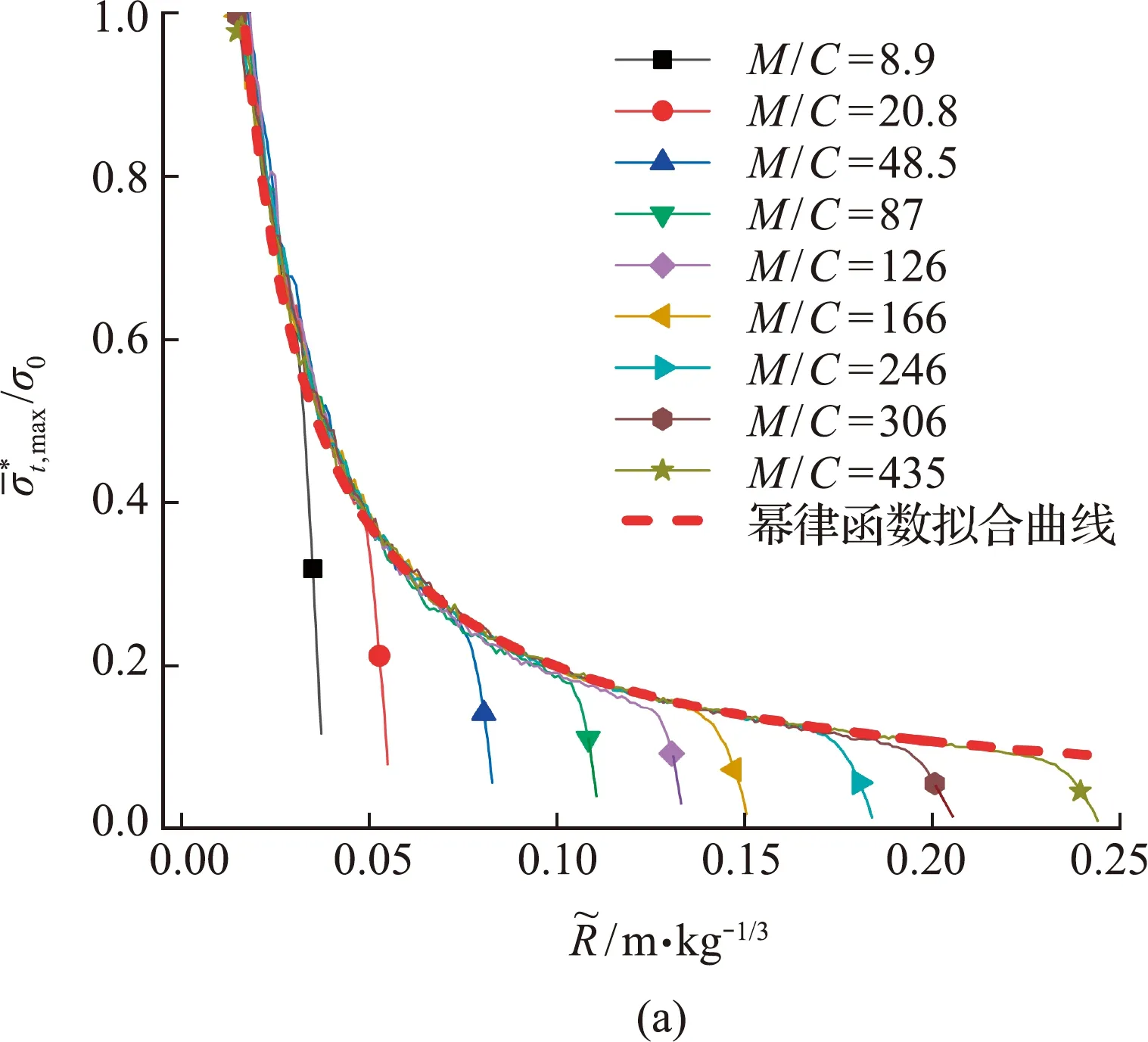
图12 不同工况下式(12)中尺寸参数和形状参数随震源比例距离的变化

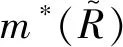
(14)

5.3 颗粒破碎体积分数随比例距离的变化

爆炸波的传播衰减、应力空间分布的非均匀(式(12～14))以及耦合颗粒破碎强度的不确定性(式(7))导致颗粒破碎概率在空间分布的强烈非均匀。

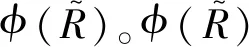
(15)

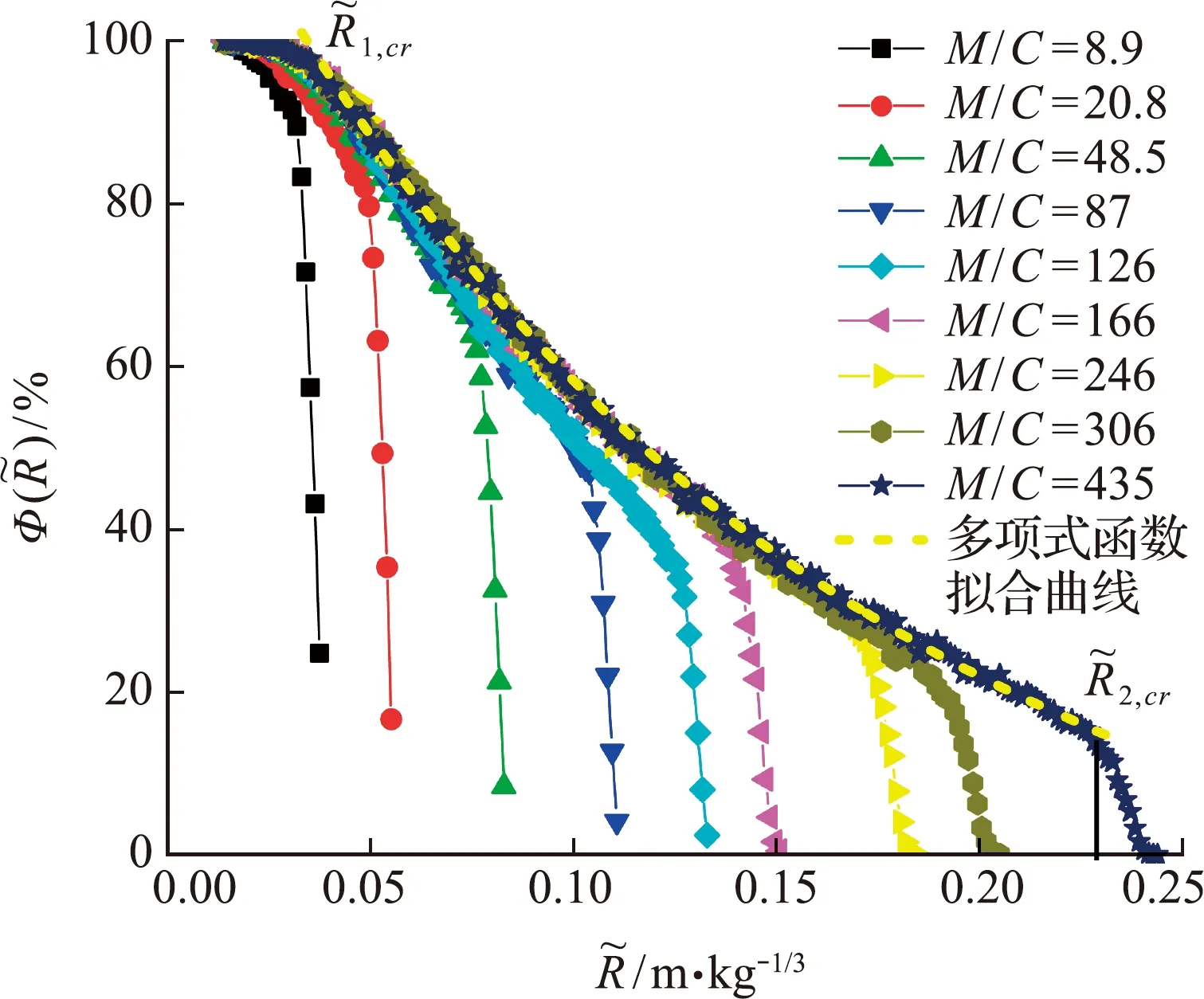
图13 不同 M /C 的颗粒环壳内颗粒破碎体积分数随比例距离的变化

(17)

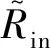
(18)

由式(11)可以得到

(19)

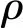
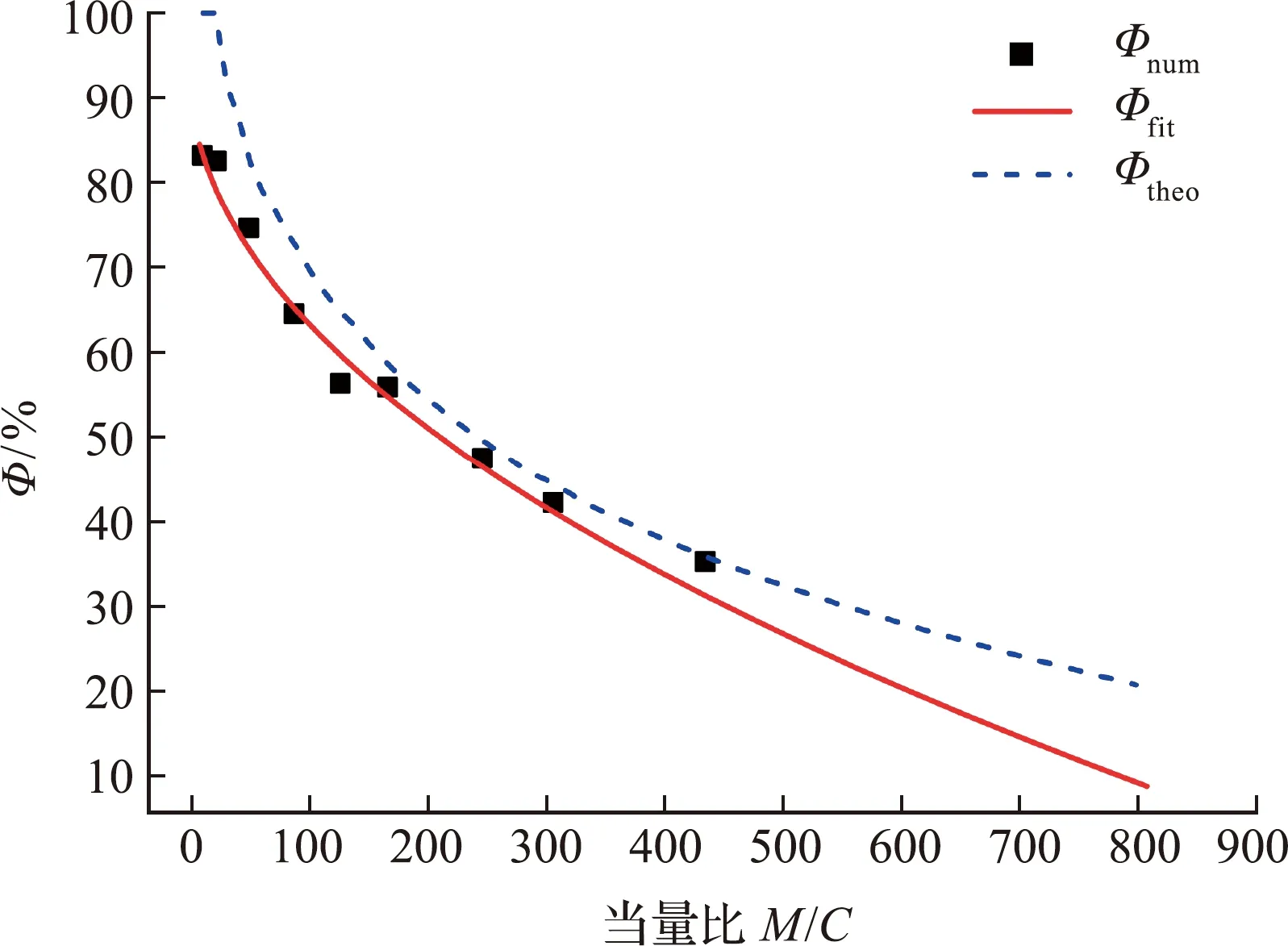
图14 不同方法得到的颗粒破碎体积分数Φ的比较

6 讨 论

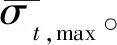
(20)

(21)

(22)

7 结 论

采用破坏波传播特征时间内颗粒的最大平均诱导应力作为颗粒的特征应力，修正了基于准静态平板压缩试验的颗粒破碎强度Weibull分布。将修正后的颗粒破碎准则应用于离散元模拟得到颗粒环壳内部的应力场，获得了与试验结果高度吻合的破碎颗粒体积分数，同时揭示了控制破碎颗粒体积分数随当量比的变化机理。将模拟得到的颗粒特征应力的概率密度分布与修正的颗粒破碎强度Weibull分布相结合，建立了二维柱装药构型中颗粒环壳中破碎颗粒体积分数的理论模型，模型预测结果与数值模拟结果具有很强的一致性。