关于采用粗粒化提高颗粒材料多尺度模拟守恒特性的研究
程宏旸, Thomas Weinhart
(特文特大学 工学院,荷兰恩斯赫德 7500AE)
1 引 言
颗粒材料如沙土、岩石、药物粉末和农业谷物等广泛存在于自然界和工业应用中。这些材料均由离散的可自由运动的颗粒集合而成。因此,其宏观尺度力学性质由颗粒间相互碰撞及微-细观结构演变决定[1,2]。
颗粒材料微观、细观结构及其空间尺度随外部荷载变化而演变,即使仅考虑固态颗粒介质(如准静态下的剪胀[3]、塑性屈服[4]、组构张量和各向异性[5,6]),其宏观尺度上的建模也可能是相当复杂的。尽管当前宏观模型可以很好地描述准静态下复杂颗粒行为,流态颗粒介质的剪切增稠、稀化[7]及分层[8]等流变现象的宏观模拟还是非常困难,目前主要依靠颗粒及细观尺度模型来进行研究。
微-宏观耦合模拟与单纯的微观或宏观模拟相比具有明显优势。通过建立合理的耦合模型,可以保持宏观方法较高的计算效率和微观方法较高的计算精度。本文主要探讨同步多尺度方法(concurrent multi-scale methods),即微观与宏观子模型在同一个计算域上求解并在时间上同步。这需要与基于微-宏观关系在物质点和表征单元之间传递的分层多尺度[9-11]耦合方法作出区分。同步多尺度方法主要分为两类,一是表面耦合,可用于模拟颗粒与可变形单元之间的相互作用;二是体积耦合,可用于模拟颗粒材料连续-非连续和流态-固态转换等复杂物理现象。
以有限元(FEM)和离散元(DEM)为例(图1),表面耦合通常依赖于DEM模型中可变形构件外表面与颗粒材料相接处的界面ΓC=ΓF E∩ΓD E。该界面接收来自FEM网格的运动信息,并且将颗粒与该界面间的相互作用力映射到FEM模型的牵引边界上。由于表面耦合通常通过狄拉克函数来实现[12],施加到FEM域上的耦合力场很可能是非光滑的,导致难以处理的累积误差。目前FEM-DEM界面耦合方法的应用,如轮胎、土工膜、土工格栅与土颗粒之间的相互作用[12,19,20],均采用基于狄拉克函数的微-宏观映射。
体积耦合又称为Arlequin多模型耦合框架,由Dhia等[13,14]提出,最初用于耦合具有不同网格分辨率的FEM模型,由Wellmann等[15]首次扩展到FEM-DEM耦合方法上。体积耦合在FEM-DEM模拟上的应用主要通过在体积重叠区域ΩC=ΩF E∩ΩD E(图1)上施加动态约束,使微观和宏观两个子模型的解尽可能一致[15]。而如何从微观颗粒运动信息中提取适应于FEM求解空间的宏观场则是需要解决的难点之一。Wellmann等[15]使用有限元形状函数构建微-宏观传递法则,将FEM-DEM体积耦合方法应用在单桩安装问题上,即在桩体周围变形较大区域使用DEM,远离桩土作用范围使用FEM,DEM域至FEM域的过渡区间则采用体积耦合方法描述。
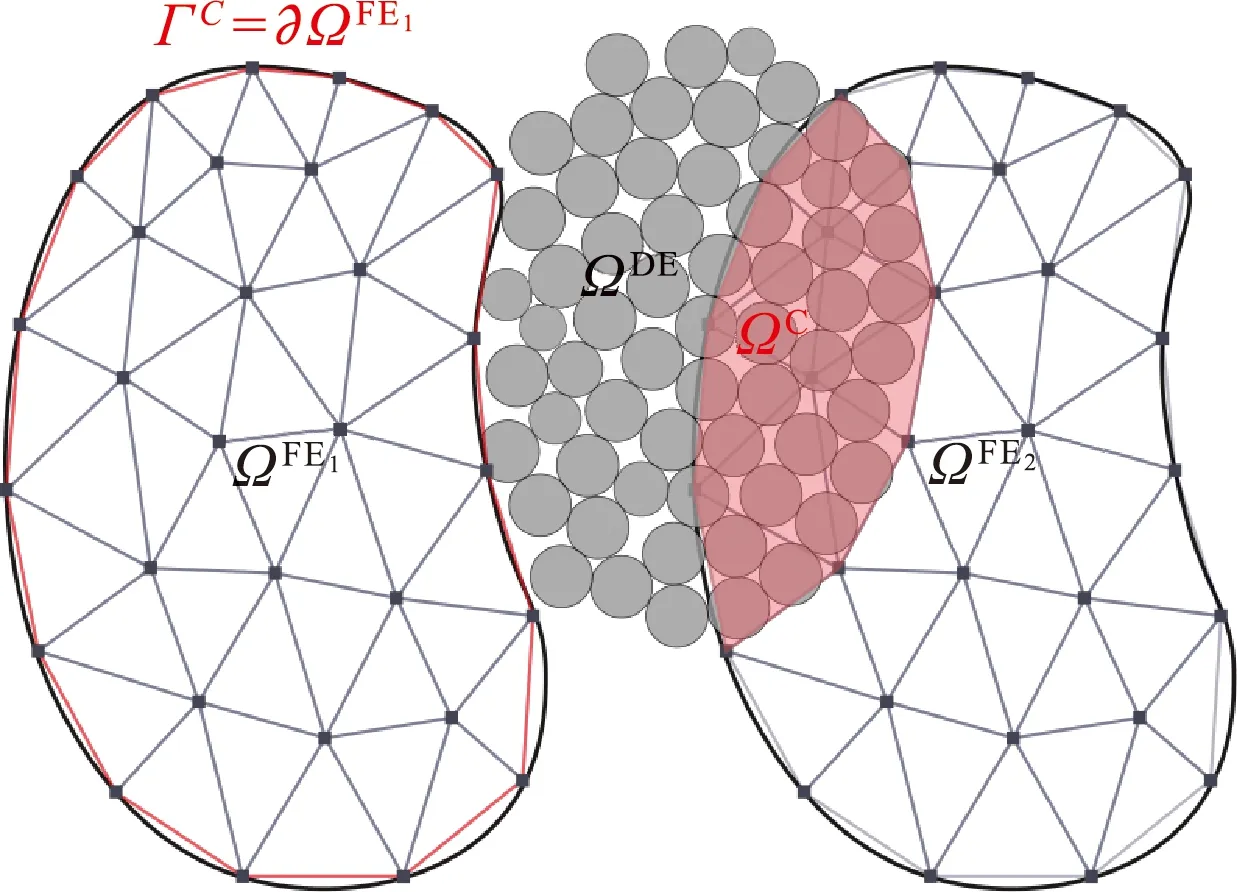
图1 同步多尺度模拟示例(ΩD E为非连续体颗粒材料,ΩF E1和ΩF E2分别为用连续体方法描述的可变形结构与连续体颗粒材料)
本文采用粗粒化(CG)方法[16],将非连续性的DEM颗粒数据首先映射到在连续体上定义的宏观场上,然后将这一宏观场耦合到FEM网格上。粗粒化操作引入了称为粗粒化宽度(CG width)的自定义参数,为均匀化后的宏观场定义了一个可调整的空间尺度。基于由粗粒化推导出的表面耦合和体积耦合项公式,将探讨如何通过调整CG宽度减小数值误差;以弹性块冲击颗粒床和离散-连续介质间的波传播两个数值算例,展示粗粒化宽度对同步多尺度耦合系统的能量守恒特性的影响,并讨论如何在保持相同能量耗散的条件下获得更高的计算效率。
2 基于粗粒化的FEM-DEM耦合方法
在同步多尺度耦合框架内,计算域Ω划分为多个子域;每个子域中的材料行为由不同子模型描述。根据特定的耦合方法,耦合区域的定义也有所不同,如ΩC=ΩF E∩ΩD E适用于体积耦合,而表面耦合区间则定义为ΓC=∂ΩF E∩∂ΩD E,如图1所示。本节将介绍如何使用CG定义空间上连续的速度场和表面牵引力场,以及如何使用这些均匀化的宏观场进行表面和体积耦合。上标DE和FE表示离散元和有限元子模型,下标{α,β,γ,…}和{i,j,k,…}则用来区分DEM和FEM模型的变量。
2.1 微-宏观传递法则
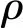
(1)
(2)
(3)
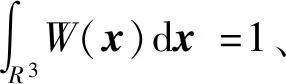
2.1.1 接触力与均匀化后的宏观牵引力
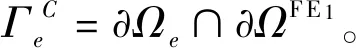
(4)
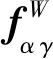
(5)

(6)
上述推导证明文献[12,17,18]广泛使用的表面耦合力公式为粗粒化表面耦合的一种特殊情况。
2.1.2 颗粒运动与均匀化后的宏观速度场
2.1.1节给出了使用CG来均匀化颗粒-结构之间接触力的一般公式。对于颗粒材料整体来说,更多情况下需要通过细观结构和颗粒运动得到相应的宏观场。本节介绍使用CG将颗粒尺度的速度或位移均匀化至宏观FEM模型上。
考虑Np个颗粒,与体积耦合域内的有限单元e在空间上重叠。由式(2)可以在耦合区间内任意位置处获得在空间上连续的速度场vC G为
(7)
式中Np为所有耦合颗粒的个数。注意,由于粗粒度函数的有效范围c有限,只有在核函数影响范围内的颗粒才会考虑在均匀化计算中。
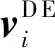
(8)
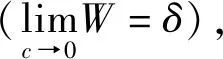
(9)
使用式(9)定义宏观速度场需要求得每个形状函数Ψi在任意耦合颗粒位置xα处的值[15],而式(8)只需要在高斯积分点上操作,后者的代码实现显然更加容易。
2.1.3 基于粗粒化的微-宏观传递的一般性
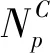
2.2 控制方程与耦合项
为了方便处理由颗粒材料碰撞、冲击和刚体运动产生的大位移,本文采用完全拉格朗日公式建立有限元模型的控制方程,以广义胡克定律描述连续体材料的应力应变关系,时间积分则采用隐式Newmark-beta法。目的是获得更高的精度来测试FEM-DEM耦合算法[19]。FEM和DEM子模型的时间步长相同,均为粒间碰撞时间tc的1/20。
颗粒尺度的力学行为则通过牛顿第二定律以及颗粒间的接触力模型求解。接触力模型通常包括法向/切向弹簧-阻尼系统,以及控制颗粒间剪切强度的摩尔库伦准则。由于接触力模型需要精确地计算颗粒间接触面积或重叠深度,离散元模拟的时间积分常采用显示Leap-frog方案。
式(5,6)给出了从DEM颗粒施加到FEM网格的节点耦合力公式。此外,FEM网格更新的位置与速度也需要通过内插传递到其在DEM域的副本上,即为颗粒提供位移边界的一组相互连接的三角形刚体上。这些三角形平面与颗粒之间的接触则采用常规的DEM接触算法来计算。
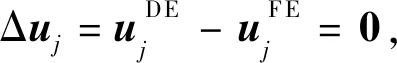

(10)
(11)
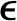
3 数值算例
基于粗粒化的多尺度耦合与传统方法相比的优势在于其可自由定义的空间尺度,使耦合物理场变得更加均匀,微-宏观传递具有非局部(nonlocal)特性。基于粗粒化的FEM-DEM表面和体积耦合方法,可以通过单球在悬臂梁上的滑动和离散-连续体材料模型内部的波传播算例进行验证。本节将通过弹性块冲击颗粒床和体积耦合深度不同的悬臂梁两个算例,研究耦合系统因表面或体积耦合产生或耗散的能量随时间的变化,并调查粗粒化宽度对耦合系统能量守恒的影响。两个数值算例的材料参数列入表1;FEM和DEM子模型的时间步长均为颗粒碰撞时间tc的1/20。

表1 有限元与离散元模型的材料参数
3.1 弹性体冲击颗粒床
首先,通过颗粒在悬臂梁上受重力作用的滑动,验证基于粗粒化的表面耦合方法。如图2所示,颗粒受重力在悬臂梁上的运动轨迹与考虑在不同接触点施加集中点力的悬臂梁弯曲(为方便获得解析解,此处悬臂梁不受重力)解析解一致。与常规局部耦合方法相比,采用粗粒化表面耦合方法获得的颗粒运动轨迹明显更光滑,由此可以推断粗粒化也使颗粒-单元间的耦合力场更光滑。

图2 颗粒受重力在弹性悬臂梁上的运动轨迹
考虑如图3所示的数值算例,检验可变形弹性块在重力作用下冲击颗粒材料时,是否因耦合作用产生多余的能量。弹性块由8个8节点六面体单元构成,在t=0时从颗粒上5d处受重力自由下落,在t=0.04 s时冲击颗粒床。耦合模拟开始之前,所有颗粒已经在重力作用下松弛至准静态,颗粒系统的动能-弹性势能比Ek/Ep低于0.01。颗粒材料的侧面为周期性边界,底部是半无限刚性墙,耦合模拟初始状态如图3所示。
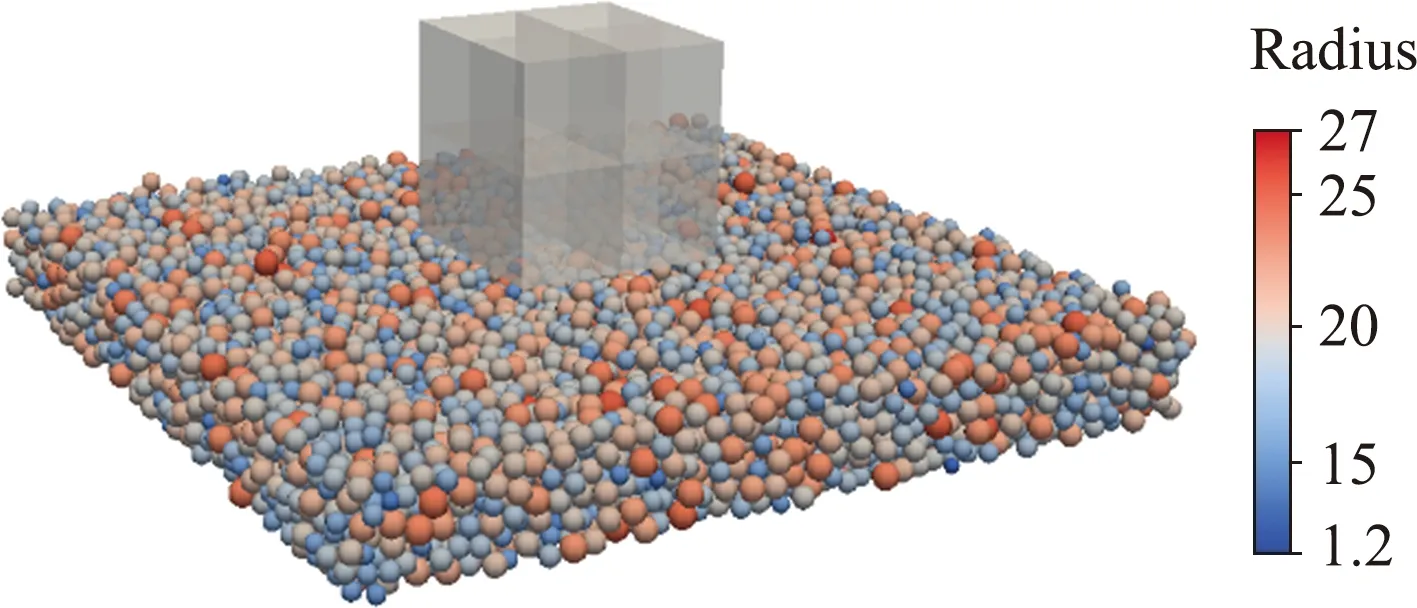
图3 FEM-DEM表面耦合模拟的初始状态
首先,考虑是否使用粗粒化进行微-宏观传递,即粗粒化宽度为0和10R的情况(c=10R)。FEM-DEM耦合模型于t=0.1 s时的模拟结果如图4所示。如不采用粗粒化进行微-宏观传递(图4(a)),即每个在耦合面上的接触力按狄拉克函数处理时,弹性块冲击进入颗粒床后不能达到力平衡状态,颗粒与单元间的耦合力不足以抵抗弹性块向下运动的趋势。采用粗粒化进行微-宏观传递时,由于每一个颗粒-单元接触力均在一定耦合半径内施加到了相邻而非单个单元上,弹性体与颗粒床的相互作用在一定时间后已趋于稳定。如图4(b)所示,颗粒床和弹性块速度远小于图4(a)中不使用粗粒化时的速度。

图4 FEM-DEM表面耦合模拟在t =0.1 s的状态(|Ve|和|Vp|分别为8节点有限单元和离散元球形颗粒的速度绝对值)
3.1.1 耦合系统总能量
图5(a)给出了FEM-DEM耦合系统z方向总动量随时间的变化。与基于CG的表面耦合方法相比,常规耦合方法不能有效降低弹性块的动量。尤其是在弹性块冲击颗粒床之后的回弹阶段,正方向的动量最大绝对值与负方向基本一致。采用CG表面耦合方法,系统的总动量逐渐减小至零,弹性块-颗粒耦合系统在t=0.1 s后快速进入准静态。
图5(b)展示了粗粒化宽度分别为0和10R的耦合系统总能量随时间的变化。可以看出,不使用粗粒化操作时,耦合系统总能量从弹性块接触颗粒床t=0.04 s时起不断增加,在回弹结束后(t= 0.07s)略微减少,并在二次下落开始时(t= 0.08 s)再次增加。由于多余的能量多以应变能形式进入FEM子模型,故有限元计算在积累误差到达一定程度后不再收敛。
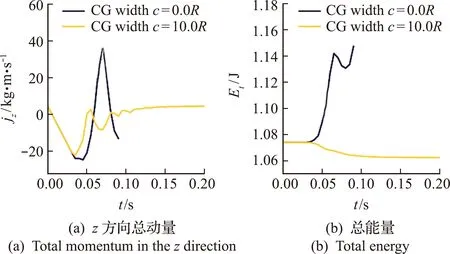
图5 采用常规耦合和CG耦合方法时FEM-DEM系统z方向总动量和总能量随时间的变化
使用粗粒化方法耦合时,系统总能量在弹性块接触颗粒床之前和耦合系统达到力平衡状态之后均不发生变化。由颗粒间摩擦产生的能量耗散仅发生在弹性体与颗粒材料间不断调整微观结构至完成动力松弛(t∈[0.04,0.14] s)这一阶段。
3.1.2 粗粒化宽度对耦合系统能量的影响
为探究粗粒化宽度对耦合结果的影响,本文选取粗粒化宽度分别为5R,10R和20R。三种情况下,耦合模拟的可视化和弹性块冲击颗粒床后达到力平衡状态的动量和能量变化与图4和图5类似。限于篇幅,本文不展开讨论。
粗粒化宽度对于耦合系统能量的影响主要体现在应变能和动能上。如图6所示,耦合系统应变能和动能随时间变化的每个峰值,随粗粒化宽度增加而逐渐减小。由此可推断,基于粗粒化的表面耦合方法可有效地处理弹性块冲击颗粒床所产生的空间、时间尺度不均匀性,减小计算累积误差,增加耦合计算稳定性。
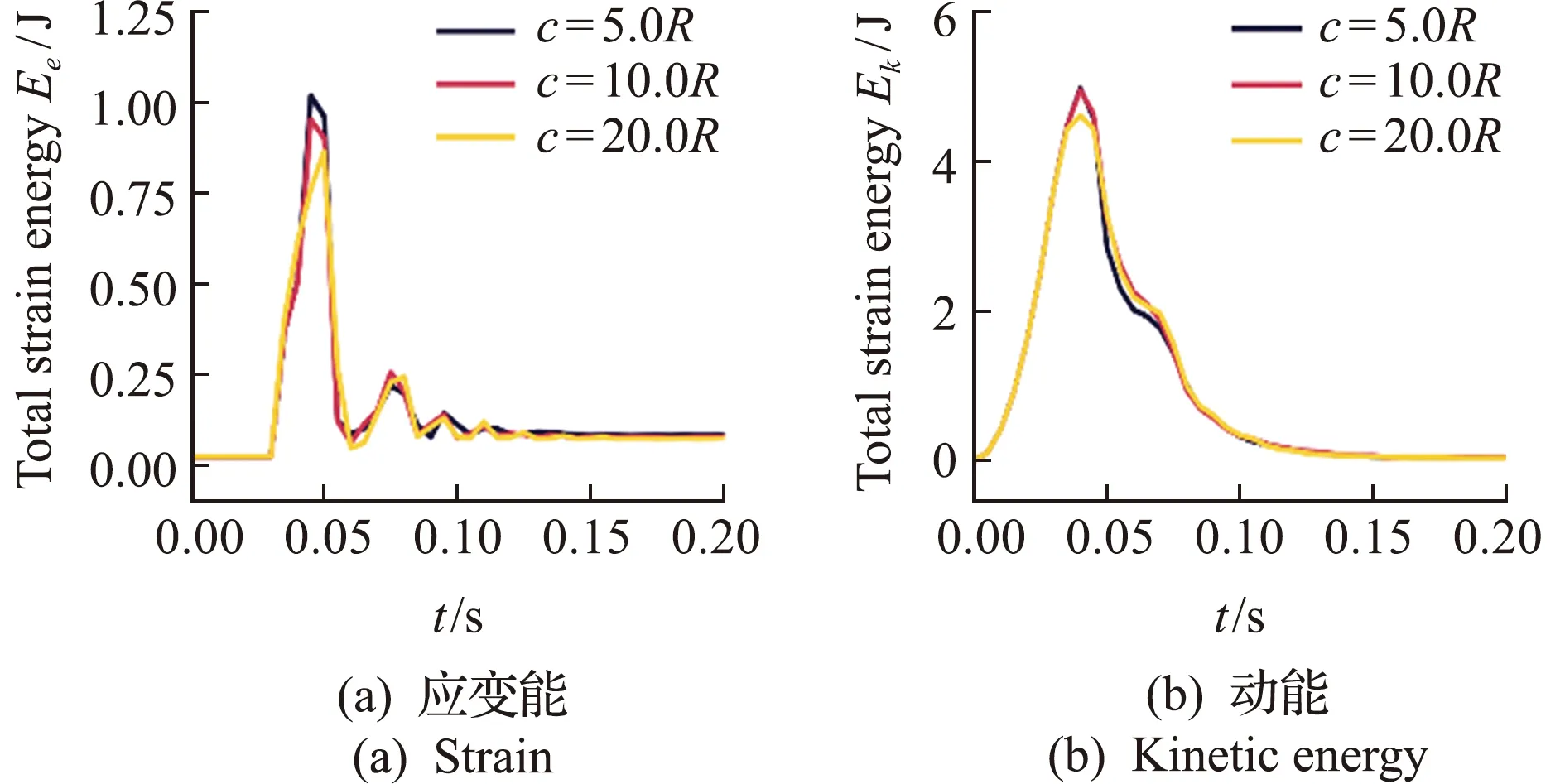
图6 粗粒化宽度对耦合系统内应变能和动能的影响
3.2 弹性波在离散-连续介质中的传播
采用FEM-DEM耦合模型对悬臂梁结构的动力特性进行数值分析,如图7所示。梁的右端FEM侧节点固定,左端DEM侧的颗粒无约束。FEM和DEM子模型均不受重力。颗粒之间拉伸与压缩的弹簧系数相同;按表1选取的弹簧系数和几何尺寸可以得到与FEM模型一致的材料参数,如弹性模量和泊松比等。
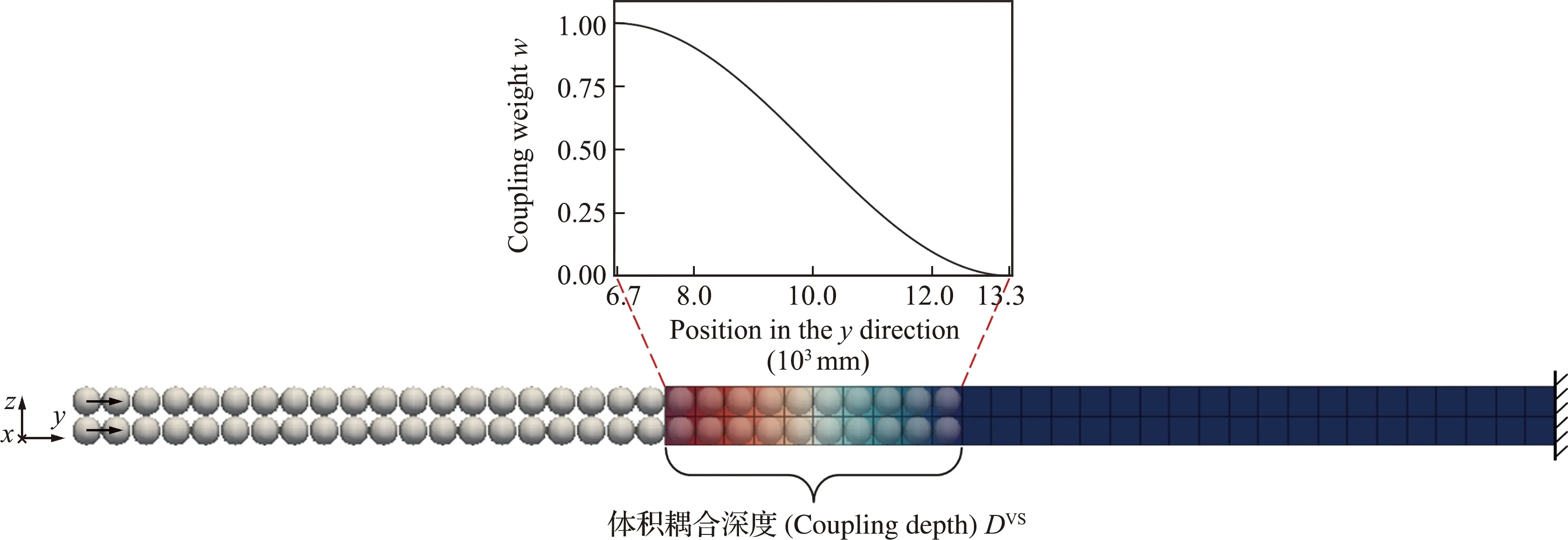
图7 采用体积耦合方法模拟的悬臂梁(耦合深度DV S=10R)
在t=0时,最左侧一层的颗粒受到初始速度v0=(0,-0.1,0) m/s的瞬时冲击,随后引起的弹性波将从颗粒系统传递到连续体系统,并在一定时间后反射回到颗粒系统。为了简化分析,每一个体积耦合单元内只有一个颗粒与之耦合。与文献[18]不同,本文同时调整两个耦合参数,即体积耦合深度(coupling depth)DV S=6R~14R和粗粒化宽度(coarse-graining width)c=0~2.5ΔX。对于尺寸相同的DEM和FEM子模型来说,耦合计算域越大,耦合模型所能描述的整体计算域越小,计算效率也就越低。本节主要分析耦合系统的总能量随耦合深度的变化,而粗粒化宽度作为均匀化的唯一参数,其取值对降低耦合系统能量耗散也是非常重要的。
3.2.1 体积耦合系统内弹性波传播的时空演变
由于方向y的波传播可以考虑为一维问题,本文取每一个x-z平面内颗粒或节点速度的平均值。以DV S=10R为例,图8给出了各个x-z平面节点/颗粒平均速度在离散颗粒系统和连续体系统内的时空演变。可以看出,弹性波由DEM子模型一端开始传入,至体积耦合区间后,以相同的波速进入FEM子模型。两子模型内波传播的波速相同且耦合区域内数值波动较小。由此可验证粗粒化体积耦合算法的准确性。

图8 颗粒系统和连续体系统内弹性波时空演化
3.2.2 耦合参数对体积耦合系统能量耗散的影响
图9给出了耦合系统(DV S=6R)总能量随时间的变化。当弹性波进入耦合域ΩC,t=0.035 s时,耦合系统总能量开始耗散,并在波峰完全离开耦合域t=0.055 s后结束。可以看出,随着粗粒化宽度的增加,耦合系统的能量耗散与不使用粗粒化情况相比明显减小。针对本节数值算例,取c=2.0ΔX或者c =2.5ΔX时,可使耦合系统总能量耗散降到最低。

图9 不同FEM-DEM体积耦合系统(耦合深度DV S=6R,粗粒化宽度c =0~2.5ΔX)的总能量随时间的变化
为了更准确地量化耦合系统的能量耗散,本文定义总能量耗散系数ΔEt/Et。从图10可以看出,ΔEt/Et随着耦合深度和粗粒化宽度的增加逐渐减小。在粗粒化宽度增加到最优值时,可以得到相对较小的能量减衰系数。耦合深度和粗粒化宽度均可以调整耦合域动态约束的均匀性,提高罚函数的约束效应。因此,增加耦合深度或者粗粒化宽度均可以得到更好的耦合效果。但增加耦合深度意味着在耦合范围内需要考虑更多的颗粒和单元,这会极大地降低计算效率。因此,更优的做法是,在ΔEt/Et相同的前提下,选择合理的粗粒化宽度,降低耦合颗粒和单元的数量。
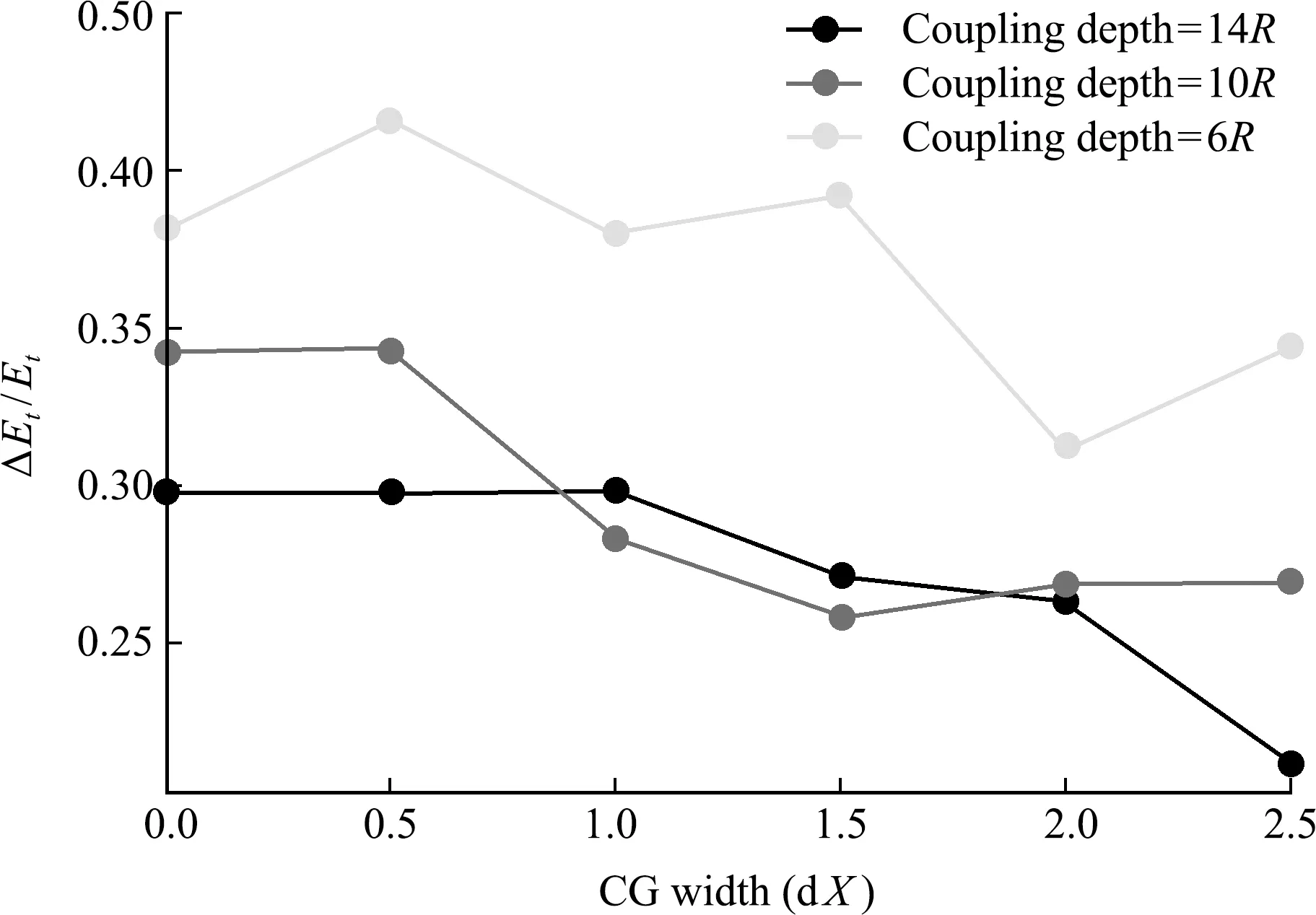
图10 FEM-DEM体积耦合系统的总能量耗散系数ΔEt/Et随粗粒化宽度和体积耦合深度的变化
4 结 论
本文介绍了如何使用粗粒化方法建立颗粒材料及颗粒-可变形构件相互作用的多尺度模型,基于微-宏观传递法则的推导,给出了基于粗粒化的FEM-DEM表面耦合和体积耦合公式,解释了为何常规局部耦合是粗粒化耦合的一个极限情况,通过两个数值算例展示了基于粗粒化的耦合方法具有更好的稳定性和更高的效率。主要结论如下,基于粗粒化的FEM-DEM耦合可以通过调整核函数影响范围,使均匀化后的DEM宏观场与FEM网格相适应;非零的粗粒化宽度使均匀化具有非局部的特性,即单元与颗粒之间不需要直接接触或重叠;较优的粗粒化宽度可以降低数值误差,使耦合模拟效率更高,尤其是在处理多个颗粒与有限单元耦合时可以避免使用较大的颗粒-单元界面弹簧,即很小的时间步长;体积耦合一般需要耦合域范围足够大以确保耦合区间较强的动态约束。合理地增加粗粒化宽度可以在保持相同总能量耗散的条件下,减小耦合域范围,提高计算效率。
综上所述,粗粒化是实现颗粒材料表面与体积多尺度模拟非常方便的数学工具。该方法在体积耦合框架下可描述颗粒材料固态-流态之间的相互转换或者材料发生的复杂物理变化,如3D打印等。在表面耦合框架下可解决诸多颗粒流与可变形结构相互作用的工程问题,如单桩安装、油井出砂、堵塞与岩石切割。

