大规模颗粒系统的精确缩尺和粗粒化离散元方法

赵婷婷， 冯云田

(1.太原理工大学 机械与运载工程学院，太原 030024；2.斯旺西大学 辛克维奇计算工程中心，英国斯旺西 SA1 8EN；3.宁波大学 冲击与安全工程教育部重点实验室，宁波 315211)

1 引 言

颗粒材料在自然界、工程应用和日常生活中广泛存在，由于其具有非连续、非均质及各向异性的特性，使得以有限元方法为代表的传统连续性数值计算方法无法准确描述其力学行为。离散元方法[1]从20世纪70年代建立后不断发展与完善，已成为探索颗粒材料物理力学性质、解决不同领域工程问题的有效数值分析工具[2]。离散元方法的优势在于可以从微细观尺度直接模拟颗粒之间的相互作用，进而反映颗粒系统的宏观力学行为。在岩土工程领域，离散元方法可以描述典型岩土材料从微观裂隙到宏观破坏的全过程[3,4]；在工业工程领域，涉及到颗粒材料的储存、混合、涂层以及运输等过程都可以用离散元方法来模拟[5,6]。离散元方法的优势也导致其在模拟工程尺度问题时会遇到计算资源不足的问题，当采用真实颗粒粒径和数量模拟实际问题时，现有的算法和计算机硬件水平难以有效支撑。真实系统的颗粒数量一般为万亿级别，现阶段离散元模拟工作的颗粒数量通常为百万至千万的水平[7-9]，虽然目前已知单卡GPU已经可以模拟1亿规模的颗粒数量[10]，工程尺度应用中面临的超高计算量问题仍无法通过现有GPU技术有效解决。

相比于直接用大颗粒代替小颗粒的做法，近些年来已有很多研究者采用粗粒化(Coarse-graining)理论来解决离散元方法在模拟工程尺度问题时计算量巨大的问题。粗粒化方法同样使用较少数量的大颗粒代替系统中数量巨大的小颗粒，其出发点在于抓住大尺度的主要物理现象，对于小尺度的相对次要的物理现象可以平均化或者忽略。从问题的物理本质来看，颗粒材料的宏观力学行为主要由颗粒的集体行为决定，而不是单个颗粒独自运动的轨迹，只要能保持颗粒材料的离散性质，就可以反映其主要特性，这就为粗粒化手段在离散元方法中的应用提供了基础。为保证通过粗粒化手段处理后的颗粒集合能真实反映原始颗粒集合的物理特性，需要在两系统间建立合理的等价关系。

国内外研究者在粗粒化理论与离散元方法结合方面开展了大量的研究工作，现有的粗粒化方法会通过缩放粒径、调整参数及修改模型等手段使得放大后的颗粒集合体仍旧可以保持原始颗粒集合的性质。文献[11-13]提出了CG模型(Coarse Grain Model)用于流化床模拟，粗粒化系统中的颗粒直径是原始系统中颗粒直径的h倍，粗粒化系统中的一个颗粒代表原始系统中呈立方体规律排列的h3个颗粒。假设原始系统中呈立方体排布的颗粒集合中每一个颗粒的平动速度和转动速度相同，且等于粗粒化颗粒的平动速度和转动速度。CG模型还假设当粗粒化颗粒发生二元碰撞时，原始集合体中的所有颗粒发生同步的二元碰撞，并将所有原始颗粒的接触力进行叠加得到粗粒化颗粒的接触力。在以上假设下，得到粗粒化系统中接触力的缩放系数为原始颗粒系统的h3倍。对于拖曳力和重力，同样推导得到了h3的缩放系数。而对于范德华力，CG模型根据能量守恒的原则进行推导，得到缩放系数为h2。文献[14-16]提出了CGSF(coarse-grained method for granular shear flow)用于模拟颗粒混合过程中的剪切流动，同样认为粗粒化颗粒代表呈立方体规律排布的原始颗粒集合，该模型只针对颗粒剪切流动的情况，在推导粗粒化系统与原始系统之间四种能量守恒关系时(动能、弹性能和摩擦阻尼粘滞阻尼能量)，重点考虑颗粒的切向运动速度。在CGSF模型简化颗粒排布几何关系和运动形式的假设下，通过对滑动摩擦系数、线性刚度系数和恢复系数进行缩放来满足能量守恒关系，得到的缩放规律较为复杂，特别是滑动摩擦系数的缩放关系还与粗粒化颗粒实时的角速度有关。CGSF模型对于滚筒中的颗粒混合过程粗粒化模拟的效果良好，但该模型缺乏广泛的适用性。文献[17,18]提出了SPA模型(Similar Particle Assembly)，将原始颗粒粒径放大h倍得到粗粒化颗粒，该模型不再对粗粒化颗粒代表的原始颗粒排布做出假设，认为粗粒化系统的颗粒排布与原始系统相似。SPA模型对控制方程中各项的缩放规律缺乏严格的理论推导，通过假设粒径对颗粒动力学行为具有决定性作用，直接将h3作为接触力、液桥力和拖曳力的放大系数。此外，不同学者提出的粗粒化模型还包括Imaginary Sphere模型[19]和Representative Particle模型[20]等。

可以看出，粗粒化方法在离散元模拟中得到了越来越多的关注，但现有的粗粒化模型大多直接从需要模拟的问题出发，通过分析问题本身的特征提出一系列假设，进而得到粗粒化与原始系统的等价关系。通过这种方式得到的粗粒化模型，尽管在特定应用中取得了比较好的模拟效果，但很难推广到其他问题中。而且由于假设的提出往往具有随意性，使得无法对原始系统与粗粒化系统计算差距的产生原因以及规模进行进一步分析。文献[21,22]从更一般的角度出发，提出了介于原始系统和粗粒化系统之间精确缩尺(Exact Scaling)系统，并且通过严格的理论推导，得到了在精确缩尺系统中颗粒集合各物理量应该满足的缩放关系。本文将在精确缩尺模型的基础上，通过多尺度方法，建立粗粒化系统和原始系统之间的缩放关系，得到离散元接触模型中相关参数的缩放定律，并通过离散元算例进行验证。

2 精确缩尺模型

原始系统、精确缩尺系统以及粗粒化系统之间的关系如图1所示，为了便于说明，图1中颗粒规则排列。原始系统和粗粒化系统占据的几何区域大小是相同的，粗粒化系统中的颗粒直径较原始系统中颗粒直径放大一定的倍数；在精确缩尺系统中，颗粒直径及几何区域较原始系统同步放大相同的倍数，可以将粗粒化系统看作精确缩尺系统的一个局部区域。需要说明的是，对于大尺度颗粒系统的模拟，精确缩尺方法和粗粒化方法并不是两种处于并列位置的方法，采用精确缩尺方法可以准确推导出原始系统小粒径颗粒集合体与放大后系统大粒径颗粒集合体之间不同物理量的比例关系。但由于精确缩尺方法会将系统的计算区域同步放大，因而原始系统与精确缩尺系统的颗粒数量保持一致，从计算效率的角度来看，精确缩尺方法在大尺度颗粒系统的模拟方面不会带来提高。但为了建立原始系统与粗粒化系统之间的缩放关系，可以将精确缩尺系统作为桥梁，首先分析原始系统与精确缩尺系统之间各物理量需要满足的比例关系。

图1 原始系统、精确缩尺系统以及粗粒化系统

2.1 相似定律

由量纲分析可知，在只考虑物体的机械运动时，任意物理量q的量纲可由国际标准单位制下的基本变量组合长度[L]、质量[M]和时间[T]推导得

[q]=LaLMaMTaT

(1)

其用向量形式的单位标准基本变量表示为

〈q〉=(aL,aM,aT)T

(2)

(3)

在由不同单位基本变量组合表示的系统中，物理量q′表示为

〈q′〉=R-1〈q〉

(4)

2.2 颗粒系统的缩放关系

(5)

在精确缩尺系统中，选取三个基本变量对应的缩放系数，分别为长度h、时间h和 密度1，即基本单元转换系数为Hb={h,h,1}，理论上三个基本变量的缩放系数可以任意选取，目前的取值组合可以为解释原始系统与精确缩尺系统之间的等价关系带来方便。由转换矩阵的逆R-1及缩放系数Hb即可推得精确缩尺系统中任意物理量对应的缩放系数

(6)

以颗粒系统中的物理量力F为例，在由标准变量组合表示的原始系统中，其量纲为

[F]=N=LMT-2,〈F〉=(1,1,-2)T

(7)

〈F′〉=R-1〈F〉=(4,-2,1)T

(8)

由式(6)可以得到在精确缩尺系统中F的缩放系数为

hF=Hb·^〈F′〉=h4·h-2·11=h2

(9)

根据以上推导，可以得到精确缩尺系统中各物理量的缩放系数，部分主要物理量列入表1，详见文献[24]。选择当前的基本单元组合以及对应的缩放系数，可以使精确缩尺系统中的应力、应变、动能密度以及应变能密度与原始系统相等，保证了精确缩尺系统与原始系统之间的等价关系。

表1 精确缩尺系统中部分物理量的缩放系数

在离散元计算中，精确缩尺系统与原始系统之间的等价关系可以通过两种方式实现，(1) 文献[24]详细讨论了对于离散元方法中不同种类的接触模型，通过保证其在应力应变形式下的表达式与缩放系数无关对接触参数进行处理；(2) 将离散元计算中涉及到的物理量完全按照量纲对应的缩放系数进行放大或缩小。以上两种方法在物理上是等价的，可以根据在已有离散元程序中实现的便捷程度进行自由选择。

由于精确缩尺模型的时间变量较原始系统放大了h倍，对应的时步Δt也会较原始系统放大h倍，在采用中心差分法进行时间积分时，两系统需要的时步数是相同的，也就是说采用精确缩尺系统代替原始系统并不能从计算效率上带来任何提高。提出精确缩尺系统的作用在于，可以从更一般的角度对粗粒化系统中颗粒层面相关物理量的处理(包括接触模型和颗粒相对速度等)给出可解释的理论依据。

3 粗粒化模型

粗粒化系统在放大颗粒粒径的同时，保持系统总体区域与原系统一致，粗粒化方法会减少颗粒数量，粗粒化系统与原始系统之间不再具有几何相似性，无法精确重现原始系统的物理性质。但在精确缩尺系统中得到的相似定律可以应用于粗粒化系统，保证粗粒化系统计算结果具有较高的精度。

取原始系统及粗粒化系统中相同几何区域的颗粒为研究对象，将图2中黑色椭圆内的颗粒集合看作代表性体积单元(RVE)。为保证粗粒化系统的离散元计算结果能重现原始系统的物理力学性质，两系统对应的RVE需要满足几何一致、质量、动量以及能量的近似守恒等条件。

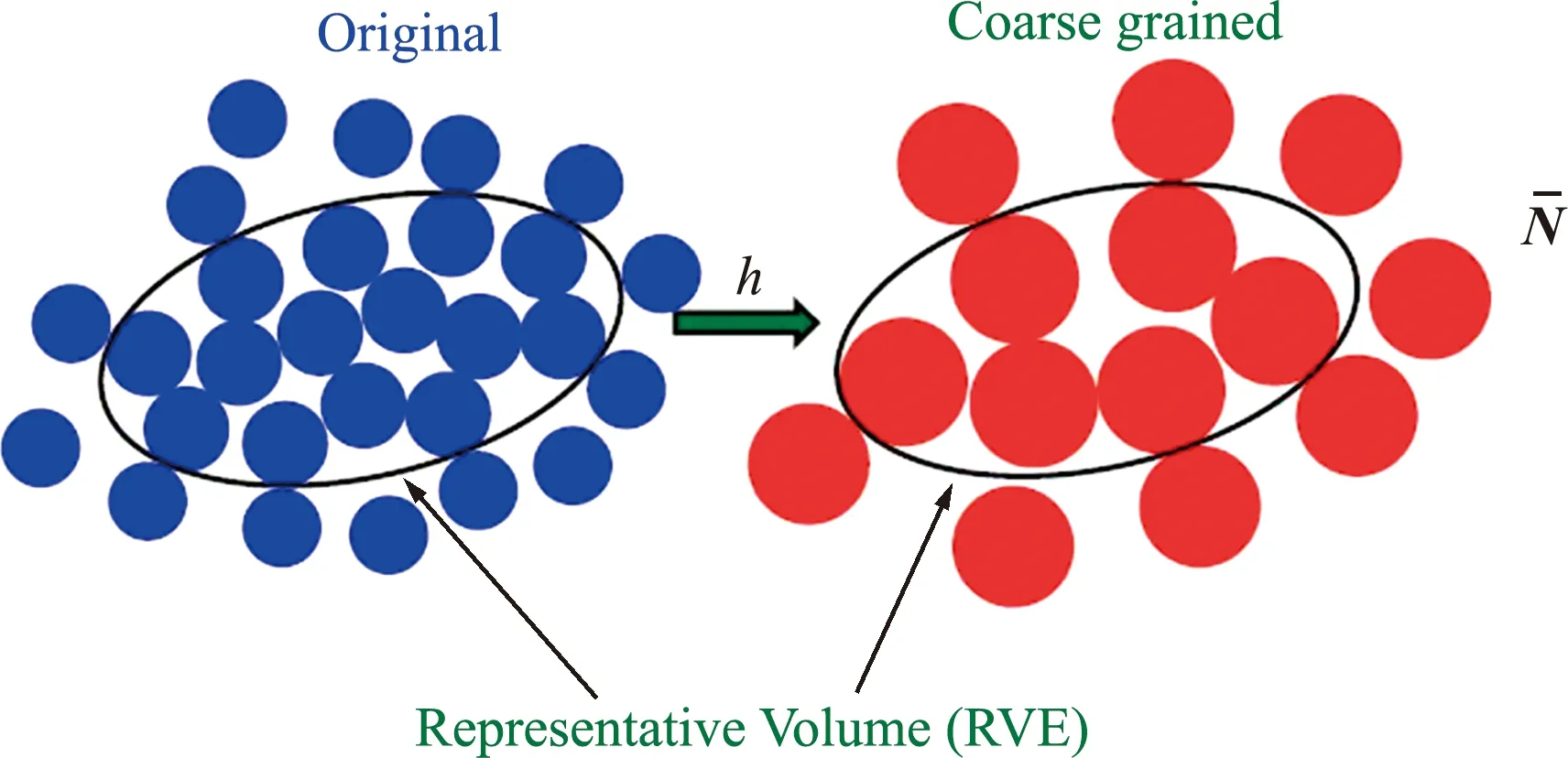
图2 原始系统及粗粒化系统中的代表性单元

(10)

在RVE边界上的颗粒接触数量满足

(11)

(12)

动量守恒的条件要求满足

(13)

能量守恒包括动能守恒、应变能守恒以及能量耗散速率守恒三个方面，动能守恒可以由颗粒质量以及速度之间的关系推导得到。

根据图3所示颗粒系统中代表性单元的接触受力情况，两系统中平均柯西应力的表达式[23]为

图3 颗粒系统代表性单元受力分析

(14)

根据式(11)，可以得到两系统中RVE单元边界接触力的缩放关系为

(15)

对于原始系统中的RVE单元，其总体平动控制方程为

(16)

粗粒化系统中RVE单元的平动控制方程为

(17)

已知在精确缩尺系统中力的缩放系数为h2(式(9))，与粗粒化系统细观颗粒尺度力的缩放系数相同，进一步分析可以发现，精确缩尺模型中提出的对于不同种类离散元接触模型的处理完全适用于粗粒化系统的离散元计算，对于离散元计算中涉及到的无量纲系数(摩擦系数、泊松比和阻尼系数等)不需要做任何缩放。可以看出，原始系统和粗粒化系统之间存在两种尺度的缩放关系，即双尺度粗粒化(Two -scale coarse graining)，细观颗粒层面相关物理量的缩放关系与精确缩尺模型得到的结果相同(如接触力的缩放系数为h2)，宏观颗粒集合层面相关物理量遵循另外一种缩放关系(如重力和拖曳力的缩放系数为h3)。

需要说明的是，以上原始系统与粗粒化RVE单元的控制方程只考虑了平动情况。对于转动情况，由于系统总体转动能无法简单地直接将各颗粒单元的转动能求和得到，所以转动相关物理量的缩放规律更为复杂。根据目前的研究，需要根据不同算例中颗粒的实际运动情况具体分析转动能的产生原因，进而得到对应的转动相关物理量的缩放系数。

对于时间变量，粗粒化系统和原始系统之间同样存在两个不同尺度的缩放关系，宏观层面物理时间的缩放系数为1，细观层面颗粒松弛时间的缩放系数为h，这就为离散元计算效率的提高带来了极大的好处。当颗粒粒径放大h倍时，颗粒数量减少h3倍使得计算效率提高h3倍，计算时步减少h倍又可以使计算效率提高h倍，故粗粒化系统的计算时间是原始系统计算时间的1/h4。

4 算例分析

两个算例证明，由精确缩尺模型推导得到的离散元接触模型相关参数的缩放关系同样适用于粗粒化系统的离散元计算。算例的不同工况都采用的是粗粒化方法，即保持颗粒集合的宏观几何尺寸不变，只将颗粒粒径进行放大。粗粒化模型通过保证任意两颗粒单元之间接触相似进而得到颗粒集合整体力学行为的相似，对于任意级配的颗粒集合都是适用的，为了便于比较不同颗粒粒径对应的计算结果，本文采用了单粒径的颗粒集合形式。

4.1 筒仓侧壁压力计算

建立如图4所示的筒仓模型，原始系统中的颗粒粒径为5 mm，将颗粒粒径放大2倍和3倍，分别采用线性模型和赫兹模型用于接触力的计算。由文献[22]可知，对于三维离散元计算，线性接触模型是尺度相关模型，当系统中颗粒粒径放大h倍时，需要将刚度系数K同样放大h倍用于计算；而赫兹模型是尺度无关模型[22]，用于不同尺度系统计算时，不需要改变接触参数。计算表2所列的8种不同工况，观察不同接触系数对筒仓侧壁压力计算结果的影响。

图4 筒仓模型及原始颗粒集合

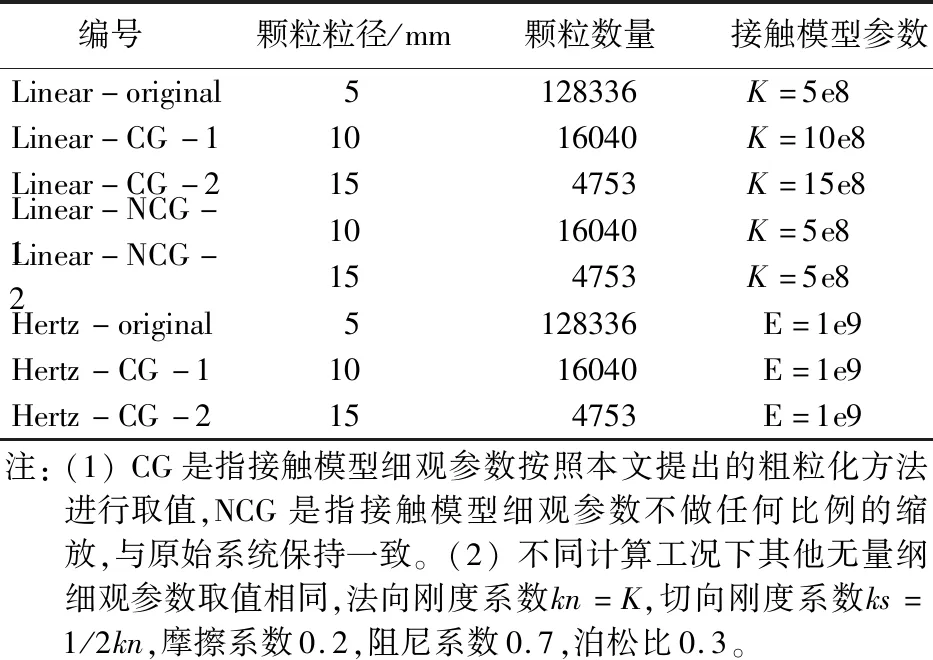
表2 筒仓侧壁压力计算工况

线性接触模型对应的计算结果如图5(a)所示，当刚度系数随着粒径变化放大相同的倍数时，筒仓侧壁压力的计算结果与原始系统的计算结果差距较小，当接触刚度系数保持不变时，粗粒化系统的计算结果无法反映原始系统的力学性质，说明精确缩尺系统推导得到的线性接触模型参数转换关系适用于粗粒化系统的离散元计算。对于赫兹接触模型，由于其具有尺度不变性，在不同尺度粗粒化系统的计算中可以选取和原始系统相同的接触模型参数，最终得到的计算结果误差较小，如 图5(b)所示。

图5 不同计算工况下的筒仓侧壁压力

4.2 休止角计算

为了验证粗粒化模型中细观层面的颗粒间接触力应该满足h2的缩放关系，采用粗粒化方法计算不同颗粒尺度对应的考虑粘聚力的颗粒材料休止角，粘聚力的计算公式[24]为

Fa=F0(1-δ/D0)

(18)

式中F0为最大引力，D0为引力范围，δ为两颗粒的重叠距离。

首先在圆筒内生成颗粒试样，将圆筒缓慢提升，颗粒在重力作用下自由滑落，形成稳定结构用以计算颗粒材料的休止角。将原始系统中的颗粒粒径分别放大2倍和3倍，将粘聚力按照h，h2和h3的缩放系数进行放大，具体工况列入表3，将计算得到的最终休止角与原始颗粒系统的休止角进行对比，如图6所示。图6(a)为当粒径的缩放系数hd=2时，三种粘聚力缩放系数hf对应的计算结果，可以看出，在粗粒化系统的缩放比例不大时，粘聚力采用平方关系或者立方关系进行缩放，都能得到与原始系统相近的结果。当粒径进一步扩大，hd=3时的计算结果如图6(b)所示，可以看出，当粘聚力按照精确缩尺模型提出的相似定律扩大h2倍时，最终得到的休止角与原始系统差距最小。将不同工况对应的计算时间同样列入表3，可以看出，粗粒化系统的计算时间近似等于原始系统计算时间的1/h4，证明了第3节对粗粒化系统计算效率提高的结论。

表3 休止角计算工况

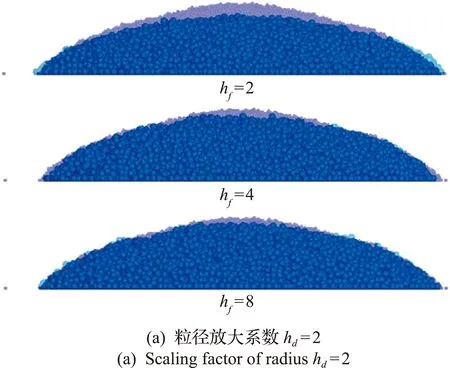
图6 不同计算工况下的休止角

5 结 论

本文针对离散元模拟大规模颗粒系统时涉及到的缩放问题，建立了一种双尺度缩放体系，并通过不同算例进行了验证。采用量纲分析的方法，得到了颗粒系统各物理量在原始系统及精确缩尺系统之间的缩放关系，为离散元接触模型中接触参数的处理提供了理论依据。采用多尺度描述方法，建立了粗粒化系统与原始系统的代表性单元(RVE)，根据不同系统RVE单元之间质量守恒、动量守恒以及能量守恒关系，得到粗粒化系统与原始系统之间宏观和细观两种不同尺度的缩放关系。在细观颗粒层面上，由精确缩尺模型得到的相似定律完全适用，即离散元接触模型接触参数应该按照文献[22]提出的方法进行处理，可以由筒仓侧壁压力及休止角的离散元计算结果进行验证。粗粒化理论可以为工程尺度大规模离散元计算提供最有效的解决办法，颗粒粒径扩大h倍，离散元计算效率提高h4倍。但目前还没有理论化的方法可以预测粗粒化系统与原始系统之间的计算误差，需要在今后的工作中展开进一步的研究。此外，在今后的工作中，还需要对转动相关物理量的缩放定律进行更深入的研究。