钟摆状态下湿颗粒坍塌流动行为及其动力相似性
吴怡淞, 王等明
(兰州大学 土木工程与力学学院 力学与工程科学系,西部灾害与环境力学教育部重点实验室,兰州 730000)
1 引 言
重力驱动质量流广泛存在于自然界和工程领域,这类复杂体系通常具有离散性、非均质和强耗散等典型特征,其屈服流动的发生和演化过程会受到众多因素的影响,不同条件下会表现出极为复杂的动力学行为[1,2]。实时原位地测量这类复杂流动过程缺乏可操作性,由于影响因素众多,很难对已发生的质量流进行有效重构,这对其流动过程的认识带来巨大挑战。因此,从颗粒物质的角度对其流动过程进行小尺度和定量化研究,这对从本质上理解这类复杂系统的流动现象及其发生机制是一种有益的探索和尝试。
颗粒物质流动相关的研究目前主要集中在干颗粒情形[3-5],而地球物理中的流动过程大多都涉及离散固体粒子与间隙液体的复杂相互作用。事实上,少量液体的存在会强烈改变颗粒系统的宏观力学性质和流动行为[6],这本质上是由于液体的出现会引发颗粒间产生粘性效应。依据系统内液体含量的差异,认为湿颗粒通常处于不同的状态,如钟摆状态、环索状态、毛细状态和浆液状态等[6]。当液体含量低于10%时,颗粒间接触点上由于液体表面张力会形成互不融合的液桥,此时通常认为颗粒物质处于钟摆状态[7]。在此状态下,液桥会促使颗粒间产生毛细力与粘滞力,进而会强烈影响微观粒子的运动[8,9],其中,相对于与颗粒间相对运动反向的粘滞力,认为通常表现为吸力的毛细力是影响湿颗粒宏观力学行为明显不同于无粘性颗粒物质的决定因素。
重力驱动下颗粒柱的坍塌是定量研究颗粒流的一种最为重要的构型,一方面是由于这类构型简单可控且流动会呈现出丰富的瞬态行为[10],另一方面则是其在地球物理和工程领域具有动力学行为相似的实际应用。目前针对干颗粒情形已开展了大量相关的研究,这些工作从不同方面研究了初始状态、颗粒属性和床面特征等对颗粒坍塌流动的动力学行为,并建立了描述其堆积形态的相关标度律[11,12]。然而,对于湿颗粒物质,尤其是系统处于钟摆状态,目前的研究工作主要集中在准静态力学性能和剪切流动行为分析方面[13,14],而对其坍塌后瞬态流动行为的研究则相对较少。Artoni等[15]基于准二维的矩形颗粒柱坍塌实验,分析了颗粒最终堆积形态与微观粒子的尺寸、液体表面张力和含水量的相关性。Li等[16]基于相似的实验装置,在更大的粒子范围内发现湿颗粒柱会发生不同的坍塌模式,基于PIV方法分析了湿颗粒的坍塌流动行为,并讨论了不同模式发生的微观机制。
钟摆状态下湿颗粒坍塌流动行为的影响因素众多,且相互之间存在耦合效应。确定主导湿颗粒动力学行为的决定因素,对从本质上理解这类复杂系统的宏观力学行为具有重要的意义。本文将首先建立能模拟湿颗粒在钟摆状态下的离散动力学模型,分析不同模型参数对系统坍塌流动行为的影响规律。在此基础上,基于动力学相似性分析提炼本质上决定不同坍塌模式发生的控制参数,这不仅可以从本质上深入理解湿颗粒在钟摆状态下的坍塌流动行为,同时能对相关实验工作的开展提供重要的依据。
2 湿颗粒离散元模型
处于钟摆状态下的湿颗粒物质中,颗粒间的相互作用力主要包括颗粒间接触力和由于液桥产生的液桥力。当两个颗粒之间存在物理接触时,接触力表现为排斥力,其大小可以用经典的Hertz-Mindlin接触模型来描述[17]。与此同时,颗粒间由于液桥的出现会产生通常表现为毛细力和粘滞力的液桥力,其大小与液桥形状、体积和颗粒间相对位置和速度等相关。
两个表面相距为δd的非接触球形颗粒间通常可以形成弯月形液桥[18],如图1所示,其中r1和r2分别为液桥回转曲面的外曲率和内曲率半径[14]。假设颗粒由液体完全湿润,三相接触角可假设为零[19]。若不考虑重力影响,液桥的弯曲面可以用Young-Laplace方程表示为

图1 湿颗粒间的液桥
(1)
式中 ΔP为液桥气-液面的压力差,γ为液体在空气中的表面张力。根据Gorge方法,颗粒间的毛细力通常由两部分构成,一部分来自于液桥气-液交界面处的表面张力,另一部分是液桥颈部横截面处压力差引起的基质吸力。考虑桥颈处的平衡,毛细力可以表示为[20]
(2)
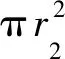
当两颗粒半径相近且液体体积相对于颗粒体积较小时,可以假设两个半填充角相等[21],弯月面曲率半径则可以表示为
(3,4)
式中 等效半径Rh=2R1R2/(R1+R2)。此时,毛细力可表示为
(5)

(6)
此时可以将液桥产生的毛细力表示为
(7)
通过考虑能量取极值时的液气表面形状,Lian等[25]建议了一个与液桥体积VL B和接触角θ相关的颗粒间临界距离D0作为判断液桥破坏的断裂距离
(8)
湿颗粒系统中,除了产生毛细力外,由于液体存在动力黏度,颗粒间相对运动时还会产生动态粘滞力以抵抗粒子的运动[26]。在离散元模型中,颗粒间法向和切向的粘滞力可以表示为
(9)
(10)

在初始的湿颗粒系统中,给定含量的间隙液体依据粒径大小以液膜的形式按比例分配到单个颗粒上,而计算过程中则采用液体迁移模型对其逐步更新。若颗粒发生物理接触,液膜会发生融合,由于接触点处的曲率较大,存在负压将液膜吸向接触区而形成稳定液桥。当两颗粒存在相对运动而逐渐分开时,液桥逐渐拉长,当超过设定的断裂距离时液桥受到破坏,液体重新分配回颗粒表面并形成液膜,直到再次与其他颗粒接触而形成新的液桥。因此,与干颗粒系统相比,钟摆状态下湿颗粒流动通常伴随着附带液膜的颗粒相互接触后液桥形成和迁移的循环过程。
3 湿颗粒坍塌流动行为分析
3.1 计算模型及相关参数
如图2所示,本文构建了一个长度为Li=50d,高度Hi=100d的矩形颗粒柱,其中d为颗粒平均粒径。模型中颗粒存在10%的粒径分散度以防止流动过程中出现结晶现象。柱体侧壁和底面均使用了与柱体颗粒相同粒径和属性的粒子固定铺设来模拟墙体的粗糙度。颗粒柱初始样本在制备开始就依据液体含量引入了液桥力,且在超过模拟仓宽度的底部平面上固定了粒径分散度为20%的颗粒来模拟粗糙水平面。当仓内颗粒达到平衡后,移除右侧墙体,颗粒柱在重力驱动下开始发生坍塌流动。

图2 湿颗粒柱初始构型(右侧为局部放大图,其中蓝色表示颗粒间形成的稳定液桥)
计算模型选取了与玻璃珠相近的材料参数,模型尺寸和相关参数列入表1,其中颗粒间接触的法向和切向刚度系数均用k0=mg/d进行了无量纲化[27]。
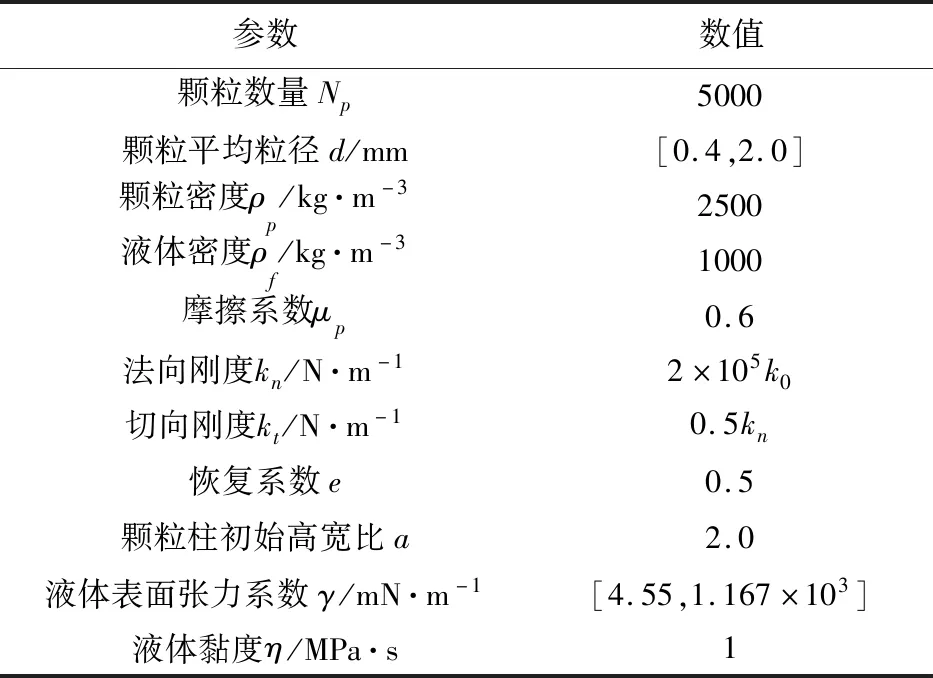
表1 模型尺寸和相关参数
3.2 模型验证
为了验证模型的有效性,本文利用和以前实验相近的计算模型[16],在含水率w=2%时,分别对两种典型粒径构成的湿颗粒柱在重力驱动下的坍塌流动过程进行了离散元模拟,最终得到的堆积形态如图3所示,其中颗粒柱的初始高宽比a=2。已有研究结果[10]表明,颗粒粒径对干颗粒柱的坍塌流动行为几乎没有影响。因此,为了对比,本文仅给出了相同条件下d=2 mm的干颗粒柱坍塌后的堆积形态。
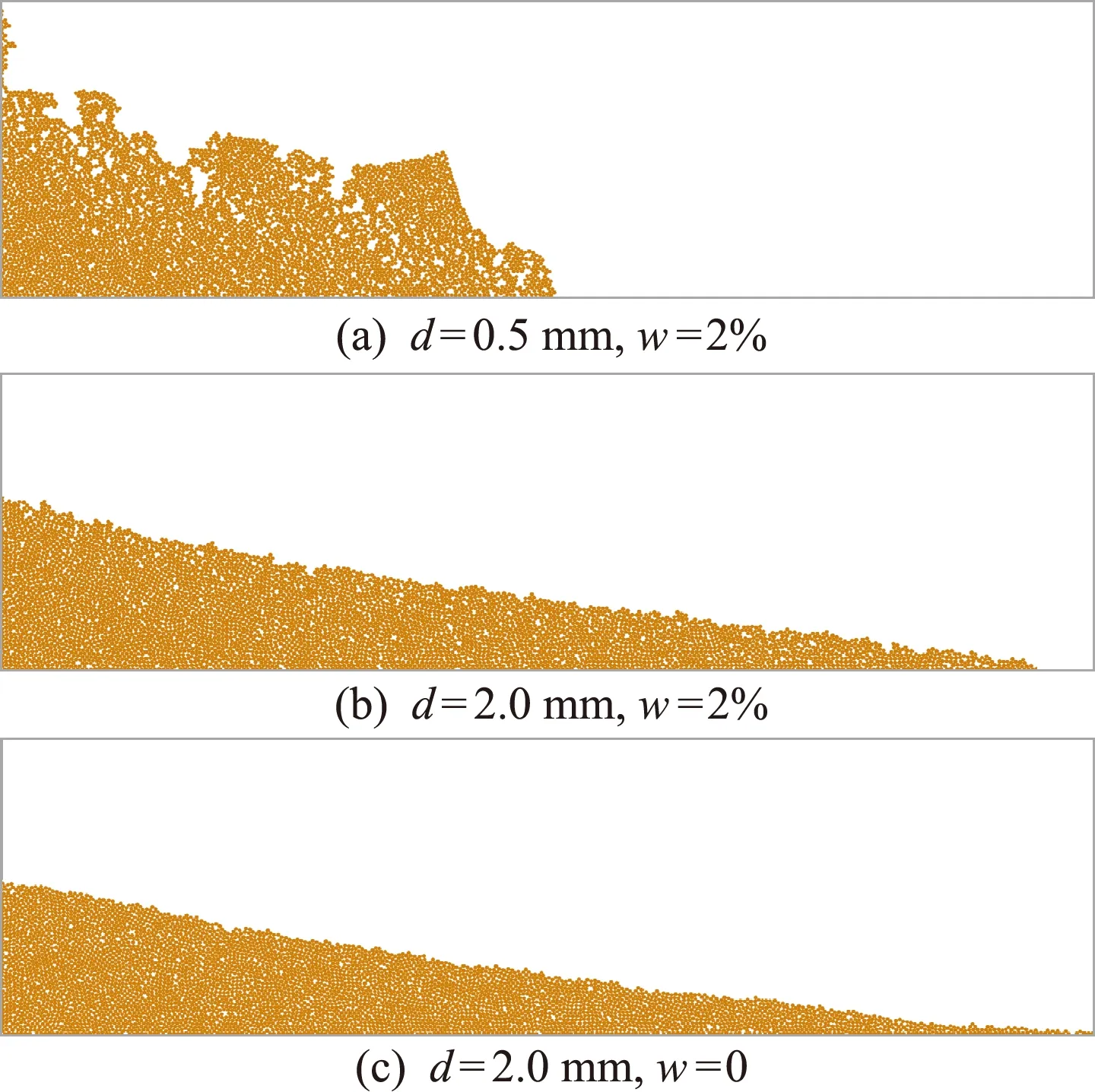
图3 不同参数下模型预测结果
可以看出,在干颗粒情形下(w=0),颗粒柱坍塌后呈现出了与以往准二维实验中观测到的相似堆积形态[10,16]。但是,当颗粒中加入一定含量的水后,不同粒径下颗粒柱坍塌后的堆积则呈现出了完全不同的形态。当颗粒粒径比较小时(d=0.5 mm),由于颗粒间毛细力作用,坍塌后形成明显的块状堆积形态,本文将其称为块体坍塌BC(Block Collapse)模式。随着颗粒粒径的增大,颗粒间毛细力与颗粒自重力相比逐渐减弱,坍塌过程中无明显的颗粒结块现象,因此其堆积高度廓线逐渐变光滑。对于粒径较大的情形(d=2 mm)可以看出,堆积形态趋于干颗粒结果,高度廓线基本近似于连续分布,本文称其为连续坍塌CC(Continuous Collapse)模式。
由此可见,粒径差异会导致湿颗粒柱坍塌后呈现出完全不同的堆积形态,这与本文相似条件下的实验观测结果基本吻合[16],表明本文建立的湿颗粒离散元模型可以较为准确地描述钟摆状态下湿颗粒柱在重力驱动下的坍塌流动行为。
3.3 坍塌流动的演化特征分析

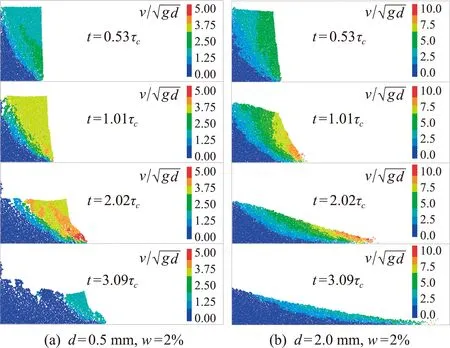
图4 湿颗粒柱坍塌后不同瞬时时刻的堆积构型和速度分布
对于块体坍塌模式,整个坍塌始于系统的整体剪切破坏,滑移面上侧块体在初期会保持初始构型并向侧前方整体滑移,在此过程中,滑移体在重力作用下会发生旋转并伴随有局部断裂现象,导致整体破碎为多个较小块体并逐渐堆积在滑移面上,而其前端块体会迅速减速并停止,最终形成明显的块状堆积形态,这种形态演化特征与本文的实验观测结果吻合良好[16]。
对于连续坍塌模式,颗粒柱体发生剪切破坏时,剪切面更偏向于柱体下部且倾斜角更小。上部颗粒在自由下落过程中会逐步在底部堆积,并开始水平向右扩展而演化为表面剪切流,颗粒内部的静态层和流动层存在明显的分界线,该界线会逐步向自由面迁移并最终达到颗粒流表层,整个流动演化过程表现出了与相同构型下干颗粒坍塌极为相似的特征。
坍塌流动前端位置随时间的演化特征如图5所示,本文给出了四种不同粒径下干颗粒(w=0)和湿颗粒(w=2%)的统计结果,其中流动前端距离和时间分别用柱体的初始长度Li和特征时间τc做了无量纲化处理。干颗粒情形下,坍塌颗粒的流动前端表现出前期加速、中间恒速和后期减速的三个典型流动阶段,流动持续时间约为3.3τc,更为重要的是粒径的变化并不会对流动的演化特征、流动距离及持续时间等产生明显影响,这和已有结果是一致的[10]。
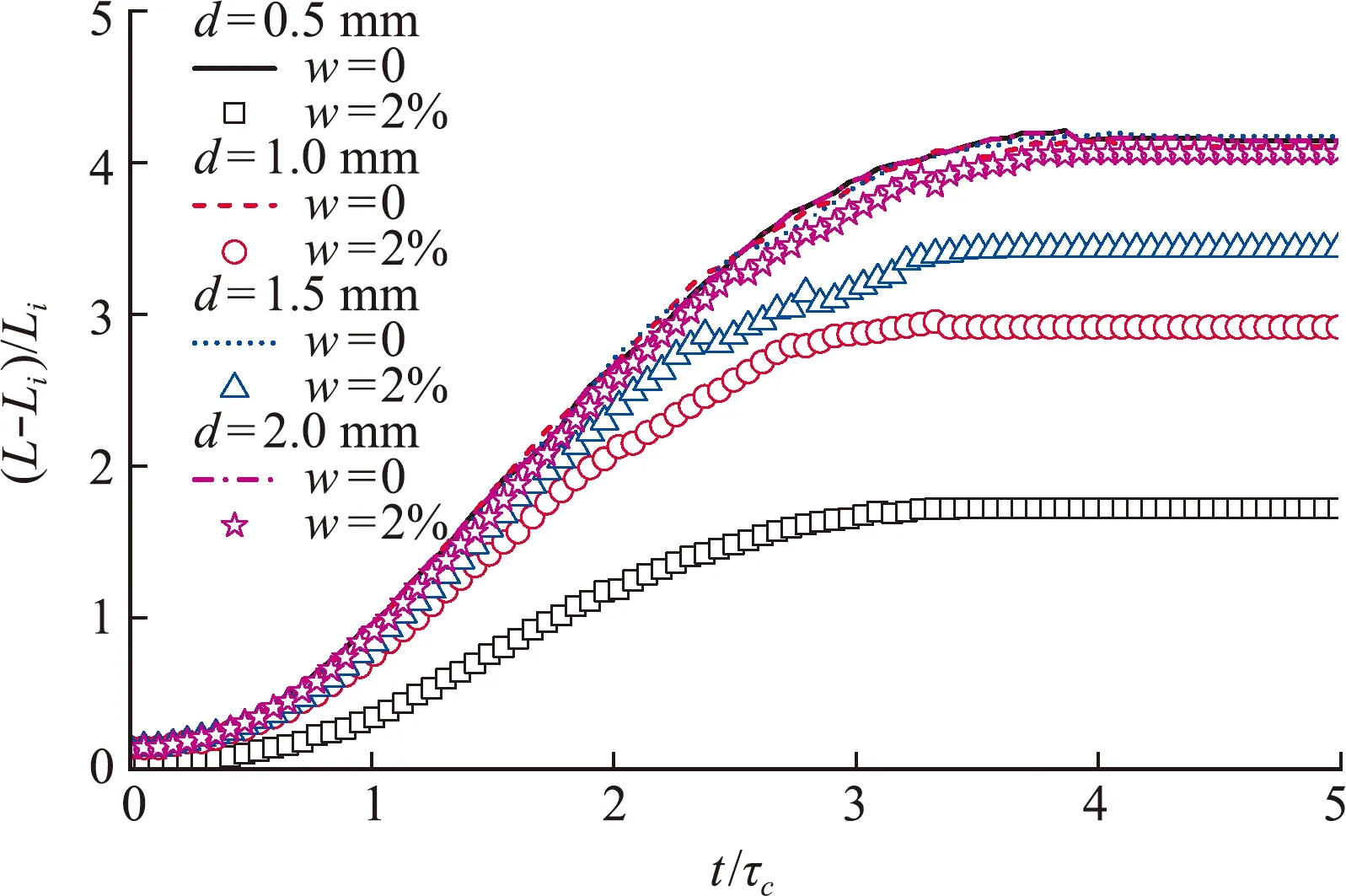
图5 不同粒径颗粒坍塌流动前端的时间演化
对于湿颗粒情形,尽管流动仍然存在三个典型阶段,但是粘性效应的出现会明显地影响流动距离和持续时间,这种影响在不同坍塌模式下是不同的。对于块体坍塌模式,流动距离明显小于干颗粒的结果,且流动持续时间更短。粒径越小,这种影响似乎越明显。当坍塌转变为连续模式时,其前端的演化特征与本文实验观测到的现象基本一致[16],即流动距离和持续时间趋于干颗粒情形下的结果。
3.4 系统参数的影响
3.4.1 粒径的影响
已有研究发现,干颗粒柱坍塌流动行为几乎不受系统内颗粒粒径大小的影响[10]。本文在保持其他模型参数不变的前提下,在含水率w=2%时,通过改变系统内颗粒的平均粒径,分析其对坍塌流动行为的影响。本文主要关心粒径对湿颗粒坍塌流动模式的影响,因此仅给出了坍塌后最终的堆积轮廓线,如图6所示。

图6 粒径大小对最终颗粒堆积轮廓线的影响
可以看出,钟摆状态下的湿颗粒物质,其坍塌流动行为会呈现出明显的粒子尺寸依赖性。当粒径较小时,湿颗粒柱呈现典型的块体坍塌模式。随着粒径增大,块状堆积形态逐渐减弱,颗粒堆积高度廓线逐渐趋于平缓,当粒径足够大时(d=2 mm),堆积表面基本趋于连续,整个系统转变为连续坍塌模式,除了堆积体前端和最高处由于粘性效应存在一定差异外,堆积廓线整体上和干颗粒情形下的结果基本一致,这与本文实验观测结果定性上是吻合的[16]。由此可见,颗粒粒径是影响湿颗粒坍塌流动模式的一个重要参数。
3.4.2 液体表面张力系数的影响
根据理论分析可知,钟摆状态下颗粒间液桥力有一部分是来自于气-液交界面处的表面张力。为此,本文重点考虑了液体表面张力系数的变化对湿颗粒柱坍塌后堆积高度廓线的影响,如图7所示,本文仅给出了粒径d=0.5 mm时的计算结果。

图7 液体表面张力系数对最终颗粒堆积轮廓线的影响 (d =0.5 mm)
可以看出,在液体含量和粒径保持不变的前提下,液体表面张力系数的增加可以引起系统坍塌从连续模式逐渐演变为块体模式,这可能是由于液体表面张力系数的增加提高了颗粒间的粘性效应导致的。与此同时,本文发现,对于不同粒径的湿颗粒柱,系统的坍塌流动都存在类似的模式转变,只是其发生转变的临界表面张力系数会随着粒径的不同而发生变化。
3.4.3 液体含量的影响
以间隙液体为水的情况,分析了含水量的变化对湿颗粒柱坍塌流动行为的影响。水的出现会使得颗粒间产生粘性,从而导致湿颗粒柱坍塌后的流动距离变小而堆积高度变大,而粒径的增大会逐渐减弱这种影响,这和本文已有的实验观测结果是吻合的[16]。当颗粒粒径足够大时(当前模型中d=2 mm),湿颗粒的预测结果定量上和干颗粒情形下的结果几乎趋于一致。
为此,本文分析了含水率的变化对于湿颗粒坍塌后堆积形态的影响。图8针对两种典型粒径,分别给出了堆积高度廓线随含水率的变化。对比结果可以看出,含水率的变化尽管会对颗粒流动距离和堆积高度产生定量影响,但似乎不会改变坍塌流动的模式。当粒径比较小时(d=0.5 mm),系统坍塌流动始终属于块体坍塌;而当粒径比较大时(d=2 mm),连续坍塌模式并不会随着系统内部的含水率而发生变化。由此可见,若湿颗粒物质处于钟摆状态,液体含量的大小只会定量地影响系统坍塌后的堆积形态,而不会改变其坍塌流动的模式。

图8 两种典型粒径d=0.5 mm和d=2 mm下,含水率对湿颗粒柱坍塌后最终堆积廓线的影响
4 动力相似性分析
不同于干颗粒物质,湿颗粒流动行为表现出对颗粒尺寸明显的依赖性,主要是与其对颗粒间毛细力的影响直接相关[6]。此外,液体的表面张力的变化也会引起系统坍塌流动模式的转变。依据颗粒自重力和颗粒间毛细力对湿颗粒柱流动行为的影响规律,两者之间的相对大小可能决定了系统发生不同的坍塌流动模式[16]。利用量纲分析,本文尝试引入一个最为简单且与上述两种因素直接相关的无量纲参数为
Bo=ρgd2/(6γ)
(11)
可以看出,基于颗粒自重力和最大毛细力比值定义的Bond数[27,28],是一个与颗粒粒径和液体表面张力系数有关而与液体含量大小无关的无量纲参数。根据第3节的分析,湿颗粒坍塌流动模式刚好由前两个因素决定而不受第三个因素的影响,因此Bond数可能是钟摆状态下湿颗粒发生不同坍塌流动模式的主导因素。
为了分析不同坍塌流动模式与无量纲Bond数的相关性,本文设计了两组典型的数值测试方案,分别对应湿颗粒的块体和连续坍塌模式。在每组模式下,考虑了大中小三组不同粒径的情况,通过调整液体表面张力系数使得对应Bond数保持不变,列入表2。为了对比,本文也提供了第三组测试方案,对应三种不同粒径的干颗粒计算结果。
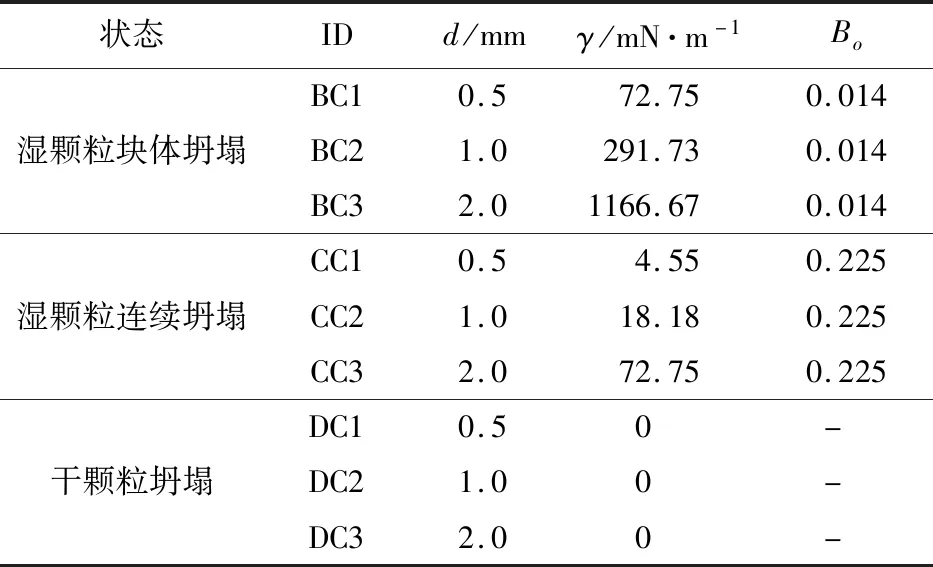
表2 用于系统动力相似性测试的模型参数
4.1 流动前端和堆积形态演化
首先分析了不同测试方案下流动前端位置随时间的演化特征,如图9所示,把同一测试方案中不同组合参数下的结果放在一起对比。可以看出,在干颗粒情形下,模型参数只有粒径发生变化,流动前端的演化表现出了明显的粒径无关性(图9(c)),且其坍塌持续时间约为3.3τc,这和以前已有的结果完全一致。
但是,在湿颗粒情形下,系统流动行为与干颗粒结果相比则发生了明显变化,如流动距离减小和流动持续时间变短等。尽管粒径和液体表面张力系数在单独变化时都会对流动行为产生明显影响,但是在保证Bond数相同的情况下,坍塌后颗粒流动前端随时间的演化则会出现明显的动力相似特征(图9(a,b)),这不仅体现在最终的流动距离定量吻合,同时体现在流动包含的三个典型阶段及相应持续时间等也基本一致。这表明在钟摆状态下湿颗粒坍塌流动中,颗粒粒径和液体表面张力系数变化时,如果保持Bond数不变,流动前端会表现出近似一致的演化特征。

图9 不同组测试参数下坍塌流动前端随时间的演化
为了进一步证实上述推测,本文给出了三个瞬时时刻坍塌颗粒的堆积高度廓线,如图10所示。可以看出,在Bond数相同的情况下,不同参数对应的瞬时堆积构型基本一致,这种坍塌过程中堆积形态演化几乎只取决于Bond数。这进一步证实在湿颗粒的坍塌过程中,系统动力学行为本质上是由该无量纲数决定,而并不单纯依赖于颗粒或间隙液体自身的属性。
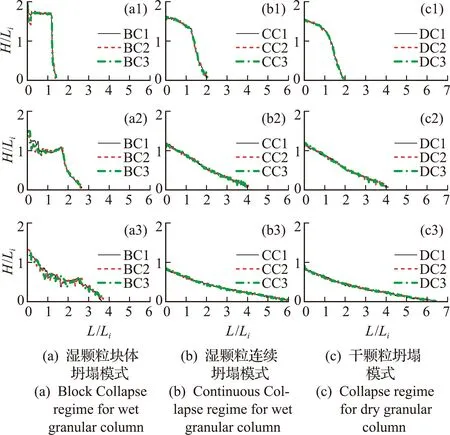
图10 不同组测试参数下三个瞬时时刻的堆积高度廓线
4.2 能量演化
能量随时间的演化通常可以用来细观地表征颗粒坍塌的动力学[29,30]。本文主要考虑了坍塌颗粒动能在两个方向上的分量随时间的演化特征。对于颗粒柱的坍塌流动,系统动能在水平和垂直两个方向上的分量可以表示为
(12,13)
式中mi为第i个粒子的质量,ui和vi分别为其在x和y方向的速度分量。
在当前构型中,颗粒坍塌流动是受粒子势能降低驱动的,因此可以用系统初始势能对上述能量进行归一化
(14)
式中hc i为颗粒质心的初始高度。
不同坍塌模式下系统动能随时间的演化特征如图11所示,其中黑色和红色分别表示系统水平和垂直方向的分动能,而不同线型则代表了同一坍塌模式中三组不同测试参数下的结果。
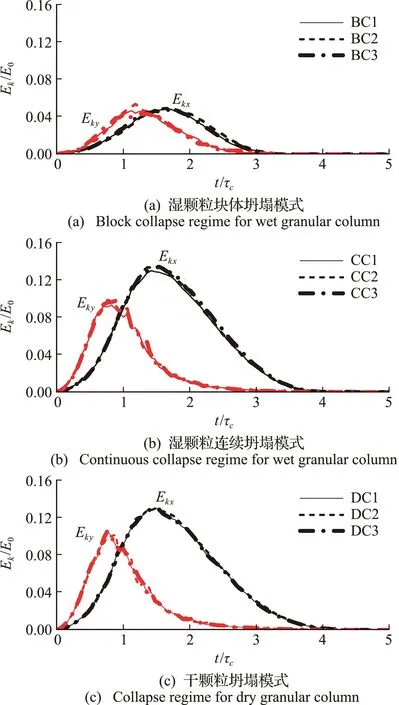
图11 不同组测试参数下两个方向分动能随时间的演化
首先,在干颗粒坍塌过程中,系统水平和垂直方向动能在坍塌初期会同时增加,后者增加更快,而前者达到的峰值更高(图11(c))。与此同时,水平方向的动能衰减需要更长的时间,大约为4倍的特征时间,这明显大于用流动前端确定的流动持续时间(图9(c))。这些演化特征表明干颗粒物质经历坍塌初期的快速自由下落后,逐渐演变为以水平扩散占主导的流动,且流动后期表现出了典型的自由表面流特征。此外,在此情形下测试参数变化是由粒径单一因素引起,由于能量演化只存在可以忽略的差异,这进一步证实粒径并不会对干颗粒物质坍塌动力学行为产生影响。
湿颗粒在连续坍塌模式下,除了能量峰值和发生时间存在一些微小的定量差异外,系统动能的演化表现出了几乎和干颗粒一致的特征(图11(b))。而对于块体坍塌模式,能量演化则发生了明显的变化,如图11(a)所示。垂向动能达到了和水平动能几乎接近的峰值,两者衰减时间的差异也很微弱,这表明系统内颗粒扩散流动逐渐弱化,而由于粘性效应形成的颗粒团簇的整体运动占主导,这可以从图4的颗粒速度分布中清晰观测到。此外,由于粘性效应增强,两个方向的动能值都明显减小,这也是此模式下流动距离明显减小而堆积高度明显增大的主要原因。
由此可见,在湿颗粒两种典型坍塌模式中,尽管颗粒粒径和液体表面张力系数的单一变化都会对系统的流动行为产生影响,但是只要保持Bond数不变,系统动能表现出了几乎一致的演化特征。
5 结 论
在湿颗粒物质中,少量液体的出现通常会引起系统流动行为发生明显变化。本文首先建立了湿颗粒的离散动力学模型,基于颗粒柱构型,定量研究了钟摆状态下液体的存在对系统坍塌流动模式和动力学行为的影响,主要考虑了颗粒粒径、液体表面张力系数和液体含量三个模型参数。模拟结果发现,粒径的变化会定性地改变湿颗粒物质的坍塌流动模式,而液体含量只会定量地影响颗粒坍塌后的堆积形态,这与本文的实验观测结果基本一致。此外,液体表面张力系数的变化会明显地改变颗粒间的毛细力大小,进而引起系统坍塌流动模式的转变。
为了分析不同模式下湿颗粒坍塌流动行为与模型参数的相关性,本文通过对颗粒粒径和液体表面张力系数两个影响湿颗粒坍塌模式的参数变化,分析了系统坍塌后流动前端位置、堆积形态的高度廓线以及系统不同方向动能随着时间的演化特征,发现尽管上述两参数在单独变化时都会明显影响系统的坍塌流动行为,但是在Bond数相同的情况下,系统坍塌后会表现出明显的动力学相似性。由此证实无量纲Bond数是影响钟摆状态下湿颗粒物质坍塌流动动力学行为的决定因素。上述结果不仅有助于从本质上深入理解湿颗粒物质的复杂流动过程,同时也可以为地球物理中大尺度质量流的连续介质模型构建提供重要的理论依据。

