复杂凸多面体随机紧密堆积组构性能的数值研究：形状参数的影响

贾明坤， 王 伟， 张 斌， 许文祥

(河海大学 力学与材料学院 固体力学研究所，南京 211100)

1 引 言

颗粒材料广泛存在于自然界和工程应用中，具有复杂的物理力学特性。颗粒体系的细观组构性能是影响其宏观物理力学性能的决定性因素[1-5]，已经有大量工作对颗粒体系的细观组构性能进行了研究。在试验研究方面，学者们利用传统物理试验获得颗粒材料的宏观性能，同时结合CT成像等技术[6,7]探究颗粒体系内部的细观组构信息，但试验过程较复杂,且价格昂贵。近年来，随着计算机科学技术的发展，数值模拟成为研究颗粒堆积行为与细观组构性能的重要手段，涌现出一大批优秀的研究成果。Zhao等[8,9]采用松弛算法，对四面体和球柱体等形状颗粒的随机紧密堆积进行了系统研究，并给出了堆积组构性能(堆积分数和配位数等)与形状参数的关联性。Jiao等[10]提出了自适应收缩元胞ASC(Adaptive Shrinking Cell)算法，获得了柏拉图粒子的最大随机阻塞堆积结构(maximally random jammed (MRJ) packings)，并讨论了柏拉图粒子的形状对其MRJ堆积分数的影响。赵仕威[2]开发非球形颗粒离散元算法，深入研究了颗粒形状对四面体和超椭球颗粒在外力作用下的随机堆积组构性能的影响。袁野[11]采用多种填充算法对超椭球和球多面体颗粒(内核为正四面体、立方体和正八面体)的无序阻塞堆积进行了研究，讨论了堆积性质与颗粒形状的复杂关联。可见，颗粒形状是影响颗粒体系组构性能的最重要因素之一，数值模拟为探究颗粒形状对颗粒体系组构性能的影响提供了强有力的技术手段。然而，目前已有成果主要集中在对规则形状颗粒(球、椭球、超椭球和正则多面体等)体系组构性能的研究，对于复杂凸多面体颗粒体系组构性能及其形状依赖性还未有报道。

数值研究颗粒体系组构性能的前提是构造颗粒的堆积结构，其核心问题包括两个,即建立单个颗粒几何模型并开发相应的接触检测算法以及开发高效的颗粒堆积算法。一方面，建立单个复杂非球形颗粒模型，通常有解析法和组合球法两种。解析法能够精确构造颗粒模型，但需要开发复杂的接触算法[12-14]实现颗粒之间的接触检测；组合球法[15]是将颗粒转化为球体的集合，通过球体的重叠判断实现颗粒的接触检测。另一方面，学者们也已经开发了很多颗粒堆积算法，包括随机有序堆积算法[16]、松弛算法[8,9,15]和离散元算法[17,18]。其中，随机有序堆积算法是一种静态堆积算法，算法流程虽然简单，但获得的颗粒堆积结构的堆积分数较低，无法达到实际颗粒材料的堆积分数；离散元算法基于牛顿第二定律模拟颗粒的真实受力情况和运动过程，但获得的堆积结构与接触力模型相关，模拟过程较为复杂；而松弛算法简单高效，且能够获得很高的堆积分数，广泛应用于颗粒堆积结构的模拟。

本文首先基于旋转椭球面黄金螺旋网格构造了一组复杂凸多面体颗粒模型(Polyκ - ng s)；然后采用松弛算法，并结合GJK算法和扩张多面体算法EPA(Expanding Polytope Algorithm)[20]，生成Polyκ - ng s多面体颗粒的随机紧密堆积结构；最后定量表征Polyκ - ng s多面体颗粒堆积体系的组构性能，并探究形状参数(长径比κ和顶点数量ng s)的影响。

2 复杂凸多面体颗粒几何模型

为了研究形状更具一般性特征的凸多面体颗粒堆积体系的组构性能，本文基于旋转椭球面上的黄金螺旋网格构造复杂凸多面体颗粒几何模型，具体步骤包括，(1) 在单位球面上生成黄金螺旋网格；(2) 将单位球面上的黄金螺旋网格映射到旋转椭球面上，生成新的复杂凸多面体。具体细节如下。

(1) 在单位球面上生成黄金螺旋网格。首先，在单位球面上进行黄金螺旋网格点采样。黄金螺旋网格点采样能够在球体表面获取均匀分布的采样点，且采样的数量可以是任意正整数。假设采样点的数量是m，则在球坐标系下第i个采样点的天顶角和方位角坐标公式[19]为

(1)

图1 单位球面黄金螺旋网格

(2) 将单位球面上的黄金螺旋网格映射到旋转椭球面上，生成新的复杂凸多面体。首先将获得的黄金螺旋网格采样点的天顶角和方位角坐标代入旋转椭球面方程，则可获得旋转椭球面上的黄金螺旋网格点，其直角坐标公式为

(2)

式中κ为旋转椭球的长径比，ng s为黄金螺旋网格点数量；然后，保持单位球面黄金螺旋网格节点之间的几何拓扑关系，则可以构造出相应的复杂凸多面体颗粒模型。本文选取的旋转椭球面长径比κ=0.4,0.6,0.8,1.0,1.5,2.0,3.0和4.0，选取的黄金螺旋网格点数量ng s=4,6,8,10，构造出一组形状按一定规律演变的复杂凸多面体颗粒，标记为Polyκ - ng s。如图2所示为κ=0.4,1.0,4.0的三组凸多面体颗粒。可见，基于黄金螺旋网格采样点构造的多面体，顶点数量可控，整体能够维持对应旋转椭球体的形状特征。

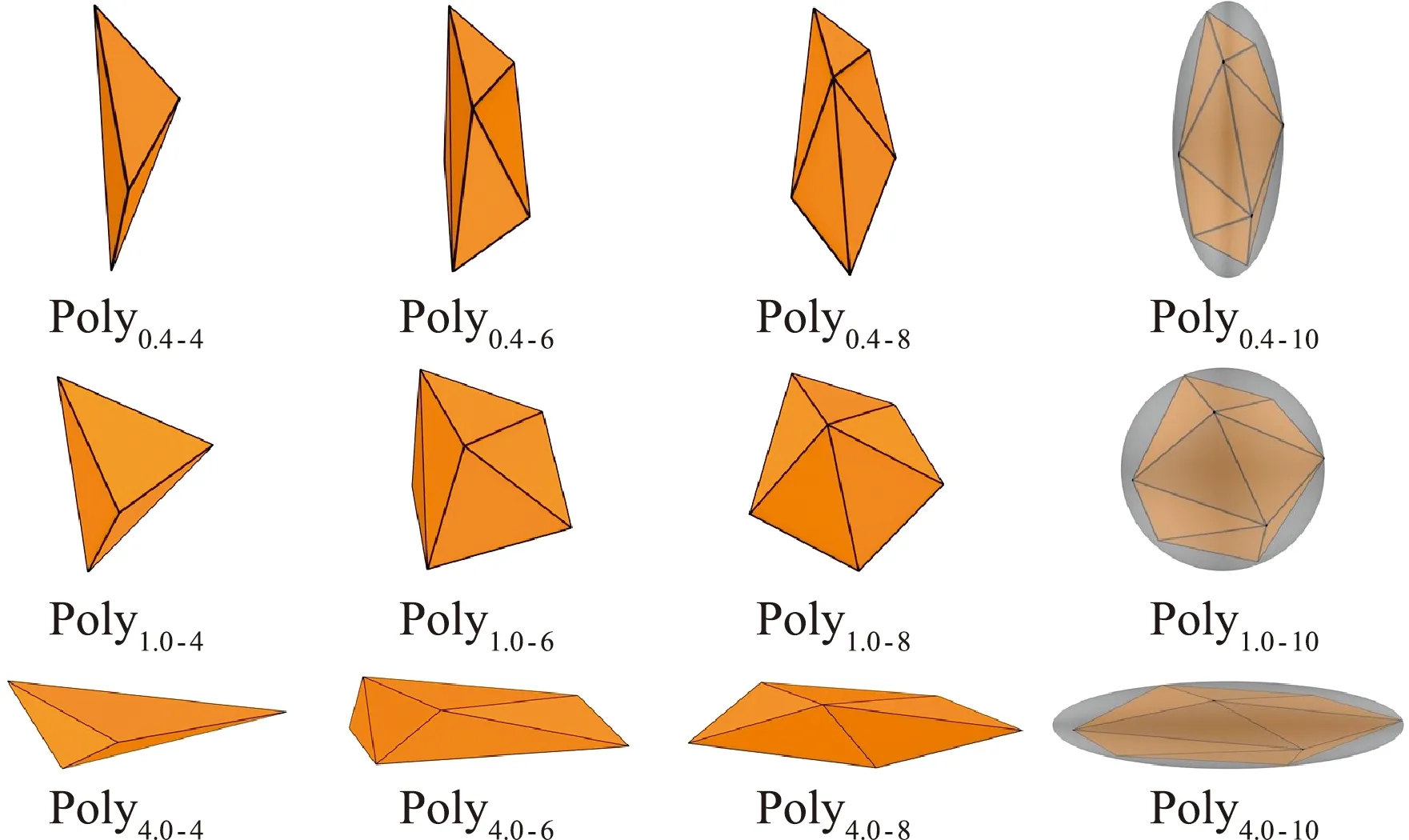
图2 复杂凸多面体颗粒模型Polyκ - ng s(κ =0.4,1.0,4.0)

可以看出，当旋转椭球面长径比κ相等时，黄金螺旋网格点数量ng s的增大使得凸多面体颗粒形状向对应κ的旋转椭球演变；当黄金螺旋网格点数量ng s相等时，旋转椭球面长径比κ的变化使得凸多面体沿着旋转椭球半轴a方向进行伸缩。同时，本文研究了Polyκ - ng s多面体颗粒的体积Vp和表面积Sp随形状参数的变化，如图3所示，在相同的ng s下，Polyκ - ng s多面体的体积和表面积随着κ的增大线性增大，这是因为κ的增大使得颗粒沿椭球颗粒长轴方向线性拉伸；在相同的κ下，Polyκ - ng s多面体的体积和表面积随着ng s的增大而增大，逐渐接近相应的椭球颗粒。另外需要说明的是，本文用于表征颗粒形状的参数，即长径比κ和顶点数量ng s无法直接用于表征工程实际中的一般颗粒，但可以找到与κ和ng s相对应的形状参数来表征一般颗粒的形态，如包围盒尺寸和圆度等[21]。

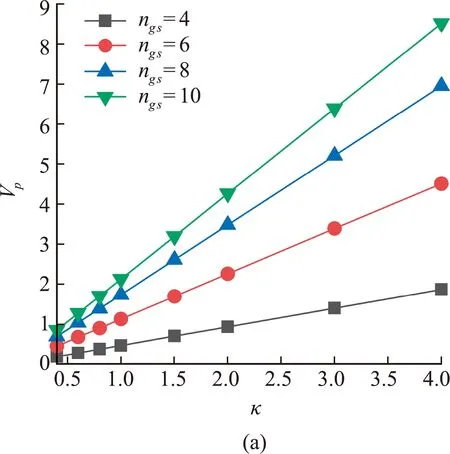
图3 形状参数对Polyκ - ng s多面体颗粒体积Vp和表面积Sp 的影响

3 复杂凸多面体颗粒随机紧密堆积

3.1 凸多面体颗粒随机堆积的松弛算法

采用松弛算法模拟周期性边界条件下复杂凸多面体颗粒的随机紧密堆积，具体实现细节如下。

(3)

式中Vi为第i个颗粒的体积。

(2) 松弛机制。首先，对堆积结构中的颗粒进行重叠检测，并求解每一对重叠颗粒的接触信息，包括接触法向、接触点和叠合量。本文采用GJK算法对凸多面体颗粒进行重叠检测，并结合扩张多面体算法EPA(Expanding Polytope Algorithm)求解重叠颗粒对的接触法向、接触点和叠合量，算法细节可参见文献[20]，本文不再赘述。如图4所示，一个四面体和一个八面体重叠，采用GJK和EPA算法可求解出接触法向n、接触点C和叠合量δ。然后，根据接触信息给颗粒施加平动和转动位移矢量以减小颗粒之间的重叠。图4的八面体获得的平动位移矢量T和绕质心B的转动位移矢量R为

图4 重叠凸多面体的接触信息与松弛位移矢量

(4)

式中α为平动系数，β为转动系数。当一个颗粒和多个颗粒存在重叠时，需要将所有位移矢量叠加，获得颗粒总的平动和转动位移矢量。对所有颗粒重叠检测、接触求解并施加位移矢量为一个松弛循环，重复松弛循环可以不断减小整个堆积结构中所有接触颗粒之间的重叠。

(3) 松弛过程的停止和堆积区域的扩张。每个松弛循环后，检测所有接触颗粒的叠合量是否小于预设值δmax，若满足，则停止循环，获得的结构即为一个满足周期边界条件的凸多面体颗粒堆积结构；若不满足，则继续松弛。重复T次松弛循环记为一个松弛迭代周期，每个迭代周期后，扩大堆积区域，即增大立方体容器边长，增长量为

(5)

mor=δ/[0.5(Re q 1+Re q 2)]

(6)

式中δ为两重叠颗粒的叠合量，Re q 1和Re q 2分别为两颗粒的等效半径，等效半径Re q和等效直径De q是用于度量非球形颗粒尺寸的参数，

(7)

式中VP为颗粒体积。

需要强调的是，在松弛算法中，只考虑了颗粒之间的法向接触和排斥作用，故只适用于无摩擦颗粒系统。

3.2 松弛算法参数取值及可靠性验证

图5 松弛过程中堆积分数p随颗粒之间最大叠合量δm的变化(Poly4 - 10)

最后，本文保持其他参数不变，δmax=10-3De q，T=100，γ=0.01，检测平动系数α和转动系数β对Poly4 - 10多面体堆积分数的影响，结果如图6所示。可以看出，对于某一固定的平动系数α，松弛堆积分数随着转动系数β的增大，先增大后减小；而对于不同的平动系数α，松弛获得的最高堆积分数相差不大。对于Poly4 - 10多面体，当平动系数α取0.75，转动系数β取1.00时，可以获得最高堆积分数为0.678，堆积结构如图7所示，图7还展示了该结构在z=0平面的截面示意图，可见，颗粒之间不存在不可接受的重叠，且结构满足周期边界条件，证明3.1节描述的松弛算法能够获得复杂凸多面体颗粒的紧密堆积结构。

图6 平动系数α和转动系数β对松弛堆积分数p的影响(Poly4 - 10)

图7 Poly4.0 - 10多面体最高堆积分数对应的堆积结构及截面

试算发现,平动和转动系数对最终堆积分数的影响最大，故本文保持其他参数不变，δmax=10-3De q，T=100，γ=0.01，改变平动和转动系数，来探索颗粒能获得的最高堆积分数。

4 复杂凸多面体随机紧密堆积的组构性能

本文研究Polyκ - ng s多面体颗粒随机紧密堆积的组构性能及其形状依赖性。根据3.2节，在松弛算法中，对于同一种形状的凸多面体颗粒，不同的算法参数取值能够获得不同堆积分数的结构。而本节研究的复杂凸多面体随机紧密堆积，不作特殊声明，默认指的是当前松弛算法能获得的Polyκ - ng s多面体颗粒最高堆积分数对应的紧密堆积结构。首先获取松弛算法下Polyκ - ng s多面体颗粒的随机紧密堆积结构；然后表征结构中颗粒体系的组构性能，并讨论组构性能与形状参数之间的关联性。

4.1 颗粒位置分布与方向分布

首先对每种Polyκ - ng s多面体随机紧密堆积结构的颗粒位置分布进行检测，在全局坐标系x，y和z方向上分别作堆积结构的截面，每个方向的截面数量取100，截面等间距，计算与截面相交的颗粒数量，并求平均值，将每个截面上与截面相交的颗粒数量与平均值之比记为该截面上颗粒的数量密度比。图8展示了图7所示的Poly1.0 - 4多面体随机紧密堆积结构的截面数量密度比，可以看出三个坐标轴方向的数量密度比均在0.85～1.2之间波动，其他形状的Polyκ - ng s多面体的随机紧密堆积结构的截面数量密度比均表现出和图8相同的规律。可见，对松弛算法获得的凸多面体颗粒随机紧密堆积结构，3个坐标轴方向上的颗粒位置分布是均匀的。

图8 图7所示堆积结构沿坐标轴方向的截面颗粒数量密度比

另外，本文计算了每种Polyκ - ng s多面体随机紧密堆积结构的径向分布函数g(r)，如图9所示。

图9 基于松弛算法的Polyκ - ng s颗粒随机紧密堆积结构的径向分布函数

可以看出，当ng s相等时，Polyκ - ng s多面体颗粒堆积结构的径向分布函数呈现相似的规律，先波动后衰减为1，当κ越接近1.0时，波动越明显，可见相应的结构在位置分布上存在长程顺序；当κ相等时，随着ng s的增大，相应堆积结构的径向分布函数的波动越明显，可见当颗粒形状接近相应的椭球时，位置长程有序性更加明显。

然后对每种Polyκ - ng s多面体随机紧密堆积结构的颗粒方向分布进行检测。使用Polyκ - ng s多面体在局部坐标系下的x轴正方向单位矢量表征颗粒方向。先根据结构中每个颗粒的方向，计算其局部坐标系下的矢量(1,0,0)在全局坐标系下的矢量，然后将该矢量分别投影到xOy，xOz和yOz平面，并计算投影矢量方向的概率分布。图10为不同形状Polyκ - ng s多面体的方向矢量在xOy平面投影矢量方向的概率分布。可以看出，松弛算法获得的随机紧密堆积结构中颗粒的方向分布不均匀，长径比κ和顶点数量ng s都对颗粒方向分布有一定的影响。长径比κ是主要影响因素，对于ng s相同的Polyκ - ng s多面体颗粒，κ越远离1，堆积结构中的颗粒方向分布越不均匀。Polyκ - ng s多面体的方向矢量在xOz和yOz平面投影矢量方向的概率分布呈现的规律与图10相似。

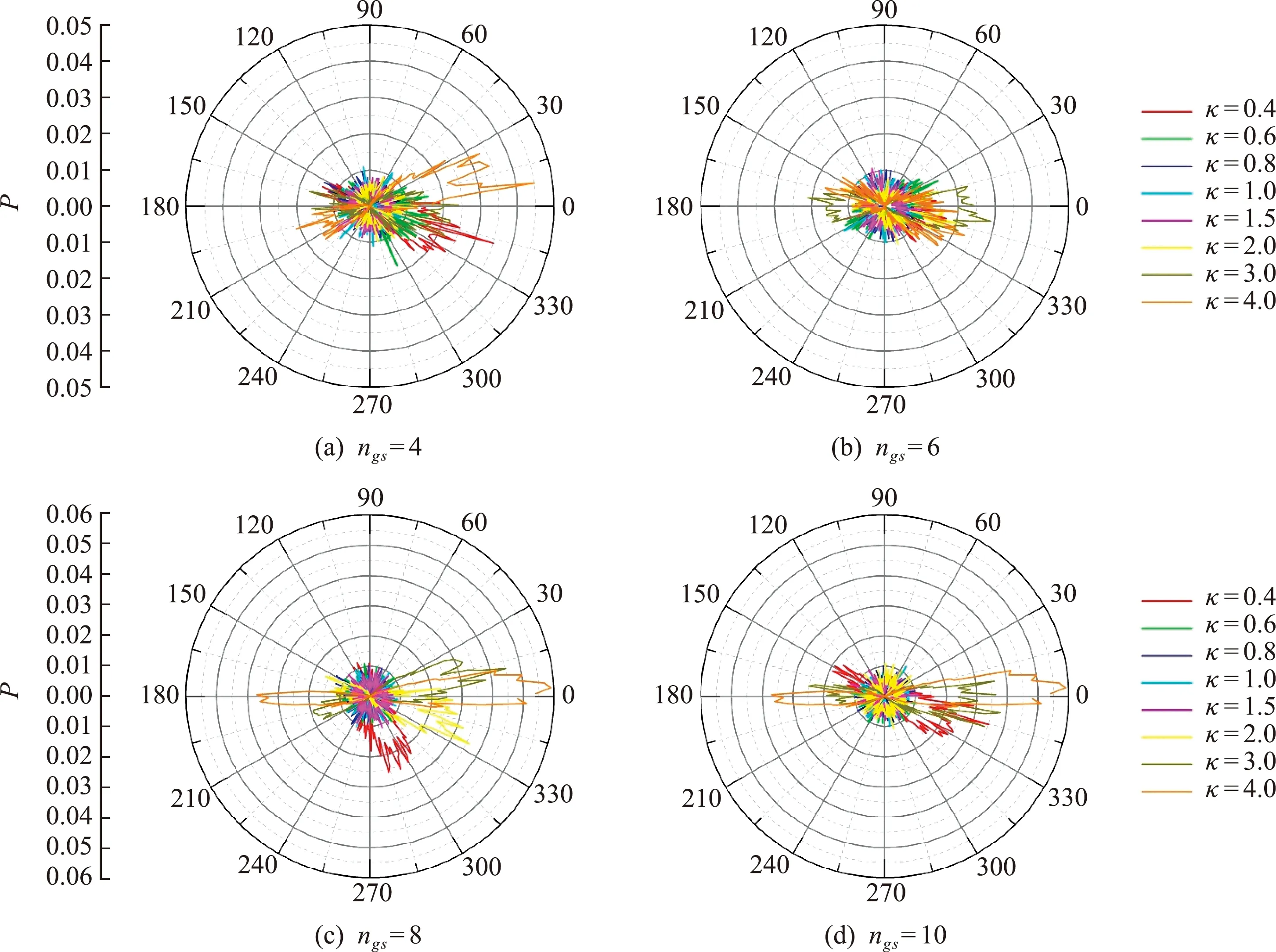
图10 基于松弛算法的随机紧密堆积结构中Polyκ - ng s颗粒的方向矢量在x Oy平面投影的概率分布

4.2 堆积分数

堆积分数是颗粒材料最重要且使用最广泛的组构性能参数，指的是颗粒体积与堆积结构体积之比。图11展示了基于松弛算法获得的Polyκ - ng s多面体颗粒的最高堆积分数。可以看出，当ng s相等时，Polyκ - ng s多面体颗粒的最高堆积分数随着长径比κ的增大先增大后减小，当κ=1.0时达到最大；对于κ相等的Polyκ - ng s多面体颗粒，当ng s=4时，颗粒最高堆积分数最低，当ng s≥6时，ng s对颗粒最高堆积分数的影响不显著；当κ=1.0且ng s=6时，堆积分数达到最大值0.720。

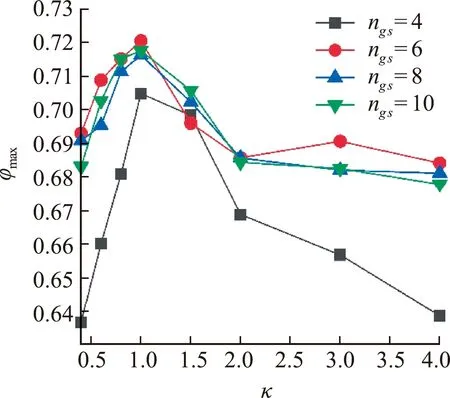
图11 基于松弛算法获得的Polyκ - ng s多面体颗粒的最高堆积分数

4.3 配位数与颗粒接触类型

图12 基于松弛算法的随机紧密堆积结构的配位数概率分布

图13 基于松弛算法的随机紧密堆积结构的平均配位数

除了配位数大小，对于多面体颗粒，颗粒接触类型更能反应颗粒堆积的紧密程度，本文对每种颗粒随机紧密堆积结构中的颗粒接触类型数量进行统计。多面体的接触类型可以划分为6种，包括点-点(v - v)、点-边(v - e)、边-边(e - e)、点-面(v - f)、边-面(e - f)和面-面(f - f)，由于 v - v 和 v - e 接触只出现在两个颗粒只有一点接触的情况，所以在堆积结构中极少出现，图14为Poly1.0 - 4多面体的 v - f,e - e,e - f和f - f 四种接触类型。图15展示了本文获得的Polyκ - ng s多面体颗粒随机紧密堆积结构中各种接触类型的接触数。可以看出，虽然所有形状颗粒堆积结构的平均配位数都在7～8.5之间，但各接触类型数量所占比例不同，f - f 接触的占比通常能够反映多面体颗粒堆积的紧密程度，f - f 接触占比随着κ的增大呈先增大后减小的趋势，与图11相应的堆积分数的规律相对应；当ng s和κ同时较大时，f - f 接触占比非常高，但此时堆积分数并不高，原因是当ng s较大时，颗粒三角面数量较多但面积较小，即使较多的 f - f 接触数也不一定有较大的有效接触面积。

图14 接触类型(Poly1 - 4多面体)

图15 基于松弛算法的随机紧密堆积结构的接触类型数量

5 结 论

本文基于旋转椭球面黄金螺旋网格构造Polyκ - ng s多面体颗粒模型，然后通过松弛算法获得随机紧密堆积结构，最后表征Polyκ - ng s多面体随机紧密堆积结构的组构性能，研究了形状参数对组构性能的影响，得出了以下主要结论。

(1) 结合GJK和EPA算法进行凸多面体接触求解，松弛算法能够用于获得凸多面体紧密堆积结构，平移系数和旋转系数对堆积分数影响最大。

(2) Polyκ - ng s多面体随机紧密堆积结构中，颗粒位置分布均匀，当长径比κ接近1，顶点数量ng s增大时，堆积结构表现出更强的位置长程有序性；颗粒方向分布不均匀，方向分布的不均匀程度主要受长径比κ影响。

(3) Polyκ - ng s多面体随机紧密堆积结构的堆积分数与长径比κ和顶点数量ng s有关。当ng s相等时，最高堆积分数随着长径比κ的增大先增大后减小；对于κ相等的Polyκ - ng s多面体颗粒，当ng s=4时，颗粒最高堆积分数最低；当κ=1.0且ng s=6时，堆积分数达到最大值0.720。

(4) 基于松弛算法获得的Polyκ - ng s多面体随机紧密堆积结构的配位数分布符合高斯分布，顶点数量ng s影响配位数分布的峰值。不同形状的Polyκ - ng s多面体的随机紧密堆积结构中的接触类型分布不同，f - f 接触占比随着κ的增大呈先增大后减小的趋势。