低调频容量高比例新能源主导局部电网低频失稳分析

齐 磊，赵 巍，孙孝峰，张 莹，王怀宝，翟燕飞

（1. 燕山大学电气工程学院，河北省秦皇岛市 066004；2. 国网秦皇岛供电公司，河北省秦皇岛市 066099）

0 引言

构建以新能源为主体的新一代电力系统是实现“碳达峰、碳中和”的关键举措。随着大规模新能源接入电网，系统重构、控制差异下的源网端将呈现强非线性、时变性、异构性，导致系统动态运行特性发生内在变化［1-2］。其中，新能源发电单元多样的环路控制形式及指令的快速响应导致电力电子变换接口与电网频繁交互，引发宽频振荡，危害电力设备及各类发电机组的稳定运行，制约新能源最大消纳水平［3-5］。

为揭示高比例新能源发电系统宽频振荡机理，国内外众多学者基于物理意义明确、阻抗方便测量的阻抗分析理论展开研究［6-11］。新能源发电单元通常经长传输线缆、变压器升压并网，网侧体现电感等效阻抗特性，导致高渗透率新能源发电系统电网强度不断削弱，电网与逆变器易交互产生谐振。在该电感等效弱网工况下，文献［8］建立了电压控制型和电流控制型逆变器阻抗模型，评估了各控制类型在高渗透率、强电网弱化工况下的高频谐振特性。同时，文献［9-10］研究了不同控制带宽下锁相环调节器参数对并网逆变器入网电流低频振荡及锁频的影响。文献［11］建立了含静止无功补偿器（STATCOM）的系统阻抗模型，探究了无功补偿装置内环控制参数对并网系统低频振荡的影响。

高比例新能源发电系统源网交互频繁发生低频振荡的同时，还会衍生耦合频率波动的低频失稳现象［12-14］。文献［15-16］指出，并网逆变器中锁相环非对称结构导致其αβ坐标系下产生相互影响的频率扰动分量，且弱电网下锁相环与电网间低频段交互影响加剧，导致振荡频率降低的同时耦合基波频率波动。同时，在新能源不参与系统调频的情况下，系统网侧频率调节特性将随着新能源渗透率的提高及电力系统惯量支撑能力的削减呈削弱趋势［17］。因此，低调频容量高比例新能源主导发电系统相比于传统发电系统抗扰性能弱，对基频波动耐受力不足，强电网弱化衍生基频大幅波动下新能源发电单元容易脱网，进一步恶化强网弱化后的电网稳定性［18］。

综上，低调频容量高比例新能源主导局部电网衍生低频振荡频率失稳对现有研究带来新要求：

1）弱化耦合机理。随着新能源渗透率的提高，网端调频容量逐渐减少，频率维持能力变弱，高渗透率强网弱化下振荡特性与基频波动特性耦合导致低频失稳发生，现有网侧电感等效的简化弱网工况无法为揭示耦合机理提供有力的分析基础。

2）基于固定基频的阻抗分析框架。阻抗分析法通过抽象电压扰动与电流扰动之间的关系可有效分析源网端交互引起的宽频振荡问题［6-11］。但对于低调频容量高比例新能源主导局部电网强网弱化后衍生耦合基频波动的低频失稳问题，基频扰动特征的缺少导致其不能准确预判系统稳定性。

本文将基波频率扰动引入传统定频阻抗模型中，基于所建立的柴油同步发电机组与新能源逆变器接口阻抗模型，构建了含电压、电流、基波频率扰动回路的新能源主导发电系统小信号框图。并根据源网端阻抗特性分析了电网强度关于渗透率、网侧等效阻抗的耦合关系。同时，构建了含基频扰动项的回比矩阵，分析了频率特性项对系统稳定性的影响，并预判了不同渗透率下系统稳定情况。且以临界稳定工况对比分析了含基频扰动模型与传统定频模型对低频失稳分析的适用性。

1 含基频扰动的源网端阻抗建模

柴油同步发电机组和分布式发电单元构成的单母线型新能源主导局部电网如图1 所示。图中：FS表示供油量齿条位移；SPWM 表示正弦脉宽调制；PI 表示比例-积分环节；PLL 表示锁相环；η为齿条控制信号；Pref为有功功率参考值；ω为系统频率；vf为励磁电压；vsg为同步发电机端口电压，vrefsg为其参考值；vd为逆变器端口电压；vc为电容电压；vo为输出电压，vod和voq分别为其d、q轴分量；iorefd和iorefq分别为输出电流参考值d、q轴分量；iL为逆变器侧电感电流；ic为滤波电容电流；io为输出电流，iod和ioq分别为其d、q轴分量；kv为电网电压前馈系数；ioabc为逆变器三相输出电流；vabc为逆变器三相输出电压；Lf为LCL 滤波器逆变器侧滤波电感；Lt为LCL滤波器网侧滤波电感；Cf为LCL 滤波器滤波电容；Rd为LCL 滤波器阻尼电阻。为分析低调频容量高比例新能源局部电网强网弱化特性及衍生的低频振荡频率失稳问题，需考虑基频扰动建立源网端小信号阻抗模型。

1.1 含基频扰动的同步发电机阻抗模型

图1 中柴油同步发电机组由采用转速下垂控制的柴油机作为原动机拖动三相同步发电机，励磁控制器调节同步发电机端电压。本文以一对极同步发电机为研究对象，建立其阻抗模型。

同步发电机三相定子绕组磁链方程、励磁绕组磁链方程、定子绕组电压平衡方程见附录A 式（A1）—式（A6）。根据文献［19］中同步发电机与三相单电感滤波逆变器模型等效思路：同步发电机感应电动势、端电压可分别等效为逆变器桥臂中点电压与输出电压，其定子电感等效为逆变器滤波电感，同步发电机励磁及调速控制环节等效为逆变器控制环节。考虑同步发电机基频扰动，其定子电枢小信号模型如附录B 图B1 所示。根据图B1，其小信号表达式如下：

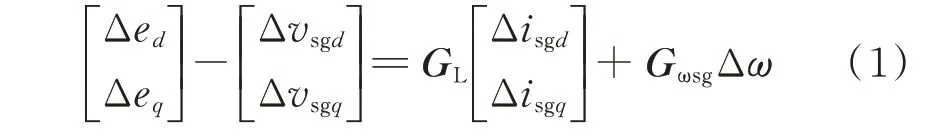
式中：Δed和Δeq分别为定子感应电动势小信号扰动量的d、q轴分量；Δvsgd和Δvsgq分别为定子电压小信号扰动量的d、q轴分量；Δisgd和Δisgq分别为定子电流小信号扰动量的d、q轴分量；Δω为系统频率小信号扰动量；系数矩阵GL和Gωsg的表达式见附录A式（A7）。

同步发电机定子感应电势的dq轴分量见附录A 式（A8），对式（A8）施加小信号扰动并展开，忽略二阶小信号扰动项并消去稳态量可得：

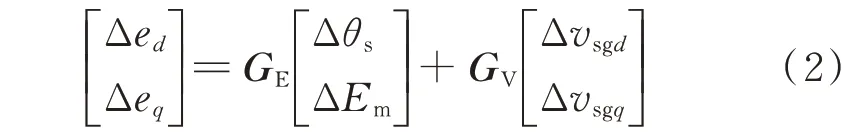
式中：ΔEm为定子感应电动势小信号扰动量；Δθs为定子感应电动势角度小信号扰动量；系数矩阵GE和GV的表达式见附录A 式（A9）。

同理，同步发电机端口电压也可列写成如式（3）所示的dq轴分量形式：

式中：Δvsg为定子电压小信号扰动量；φ为同步发电机功率因数。

接下来，对同步发电机励磁与柴油原动机转速控制环节进行建模。同步发电机采用标准IEEE AC1A 型励磁系统，如附录B 图B2（a）所示，含有下垂特性的柴油原动机控制框图如附录B 图B2（b）所示。图B2 所示励磁系统与转速控制器传递函数GEu和Gωp的表达式见附录A 式（A10）和式（A11）。根据式（A10）和式（A11）可得同步发电机控制环节小信号表达式为：

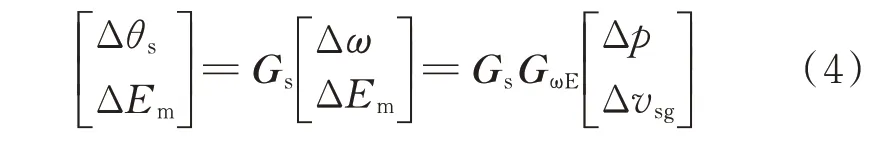
式中：Δp为同步发电机输出有功功率小信号扰动量；系数矩阵Gs和GωE的表达式见附录A式（A12）。

式（4）中，柴油同步发电机组输出有功功率可通过瞬时无功理论获得，其小信号表达式如下：

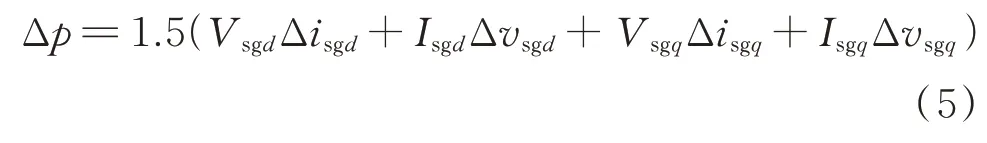
式中：Isgd和Isgq分别为同步发电机输出电流稳态量的d、q轴分量；Vsgd和Vsgq分别为同步发电机端电压稳态量的d、q轴分量。

结合式（3）和式（5）可获得柴油同步发电机组有功功率及端电压小信号表达式：

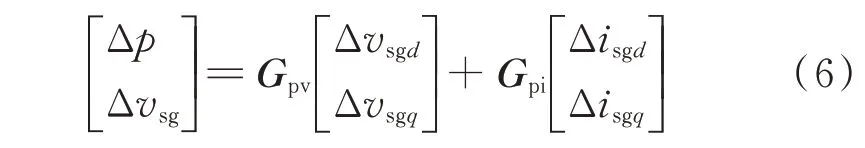
式中：系数矩阵Gpv和Gpi的表达式见附录A 式（A13）。

结合式（1）、式（2）、式（4）、式（6），可以推导出考虑基频扰动后柴油同步发电机组输出电流扰动对输出电压扰动及基频扰动的表达式，分别如式（7）和式（8）所示。

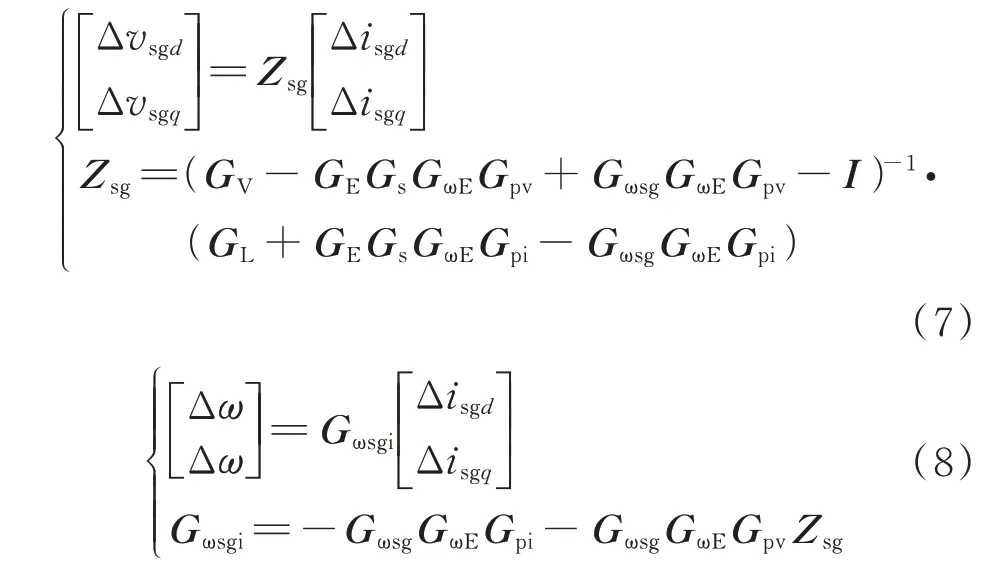
式中：I为单位矩阵。

1.2 含基频扰动的逆变器阻抗模型

图1 中分布式发电单元采用单电流环控制的LCL 逆变器作为电力电子接口单位功率因数并网，考虑低调频容量高比例新能源主导局部电网中小容量柴油同步发电机组与大规模逆变器间的频率扰动回路，含基频扰动的逆变器主电路小信号模型如下：

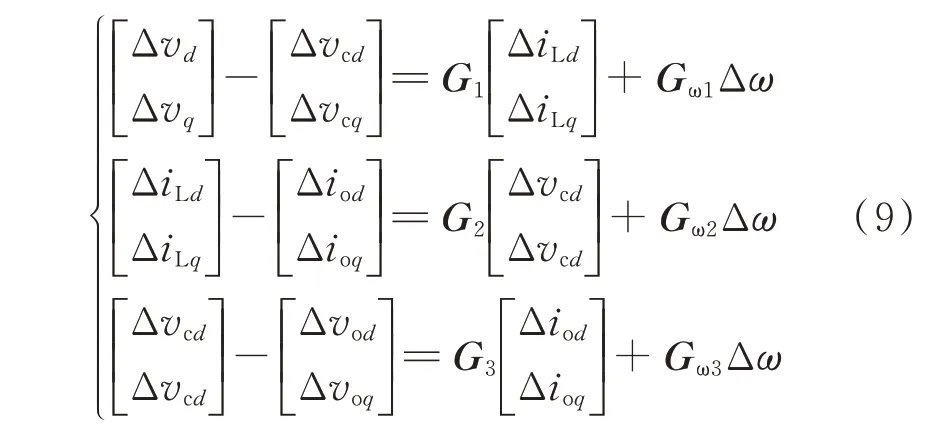
式中：Δvd和Δvq分别为逆变器端口电压小信号扰动量的d、q轴分量；Δvcd和Δvcq分别为电容电压小信号扰动量的d、q轴分量；Δvod和Δvoq分别为输出电压小信号扰动量的d、q轴分量；ΔiLd和ΔiLq分别为逆变器侧电感电流小信号扰动量的d、q轴分量；Δiod和Δioq分别为输出电流小信号扰动量的d、q轴分量；系数矩阵G1、Gω1、G2、Gω2、G3和Gω3的表达式见附录A 式（A14）。

新能源并网逆变器需采用如附录B 图B3 所示的锁相环同步，实现单位功率因数控制。随着新能源渗透率的提高，当柴油同步发电机组维持的并网点频率出现波动时，由于锁相环的动态响应，控制坐标系与系统坐标系将产生相角差θ，系统坐标系下电压、电流、占空比向量通过旋转矩阵Ts转换到控制坐标系，其转换关系见附录A 式（A15），对其电压向量表达式施加小信号扰动，忽略二阶小信号扰动项并消去稳态量可得其小信号表达式如下：

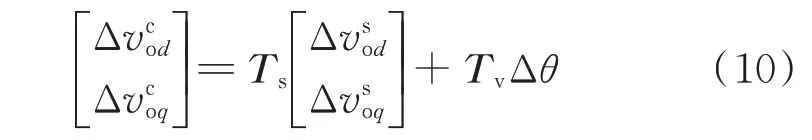
式中：Δv和Δv分别为控制坐标系下输出电压小信号扰动量的d、q轴分量；Δ和Δ分别为系统坐标系下输出电压小信号扰动量的d、q轴分量；Δθ为系统坐标系与控制坐标系的相角差扰动量；系数矩阵Ts和Tv的表达式见附录A 式（A16）和式（A17）。

根据附录B 图B3，可知控制坐标系与系统坐标系相角差小信号表达式如下：

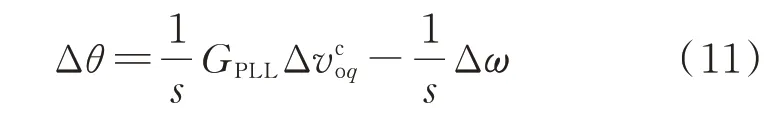
式中：GPLL为锁相环传递函数。

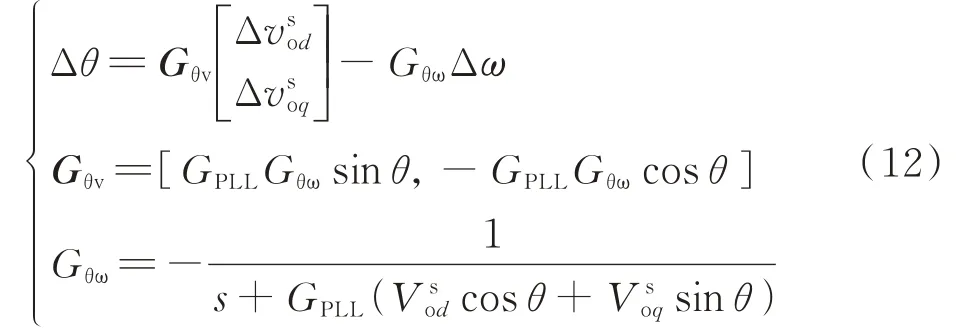
式中：V和V分别为系统坐标系下输出电压稳态量的d、q轴分量。

将式（12）代入式（10），可得控制电压扰动关于系统电压扰动及系统频率扰动的小信号关系，即

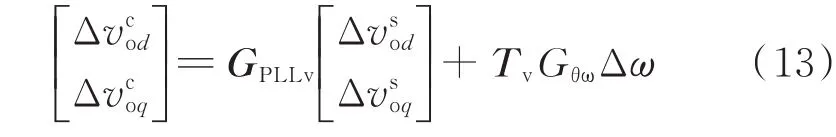
式中：GPLLv=Ts+TvGθv。

同理，考虑系统坐标系与控制坐标系的转换关系，逆变器输出电流、占空比小信号模型如下：

电流环小信号的表达式如下：

式中：系数矩阵Gci和kv的表达式见附录A 式（A19）。

控制环路数字控制延迟等效环节Gdel及电压、电流采样延迟等效环节k的表达式见附录A 式（A20）。结合式（9）、式（13）—式（15），消去中间变量，可以推导出并网点电压扰动及基波频率扰动对逆变器输出电流扰动的表达式如式（16）所示。

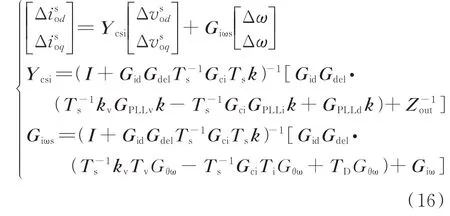
其中

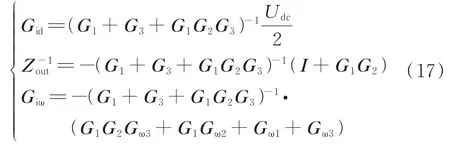
式中：Udc为逆变器直流母线电压。

2 高比例新能源主导局部电网低频失稳分析

随着局部电网内新能源发电比例的提高，同步发电机发电容量逐渐降低，对于低调频容量高比例新能源主导局部电网，电网电压频率维持能力及电网强度呈现弱化新形态。基于第1 章所推导的含基频扰动的同步发电机、逆变器阻抗模型，本章从强网弱化特性出发，对同步发电机-逆变器系统低频失稳机理展开研究。

2.1 新能源主导局部电网强网弱化特性分析

同步发电机与逆变器电气参数、稳态功率点变化均会影响系统的动态行为。基于第1 章源网端阻抗模型，探究渗透率与电网弱化及低频振荡耦合频率波动失稳现象发生的演化关系。

短路比通常用于评价电网强度［8］。考虑新能源并网台数与网侧等效阻抗，可改写如下：

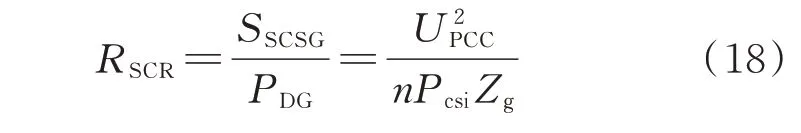
式中：RSCR为短路比；SSCSG为电网短路容量；PDG为新能源并网功率；UPCC为并网点电压；Pcsi为单机逆变器功率；n为逆变器并网台数；Zg为电网侧等效阻抗。

渗透率用于评价新能源发电占比，如式（19）所示。

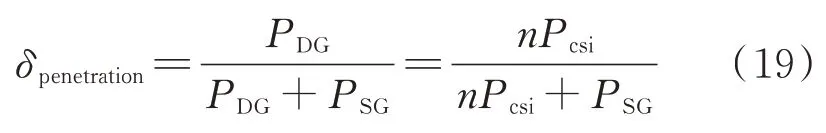
式中：δpenetration为渗透率；PSG为区域电网额定功率。

将式（19）代入式（18）消去nPcsi，可得电网强度与新能源渗透率和电网侧等效阻抗之间的关系。

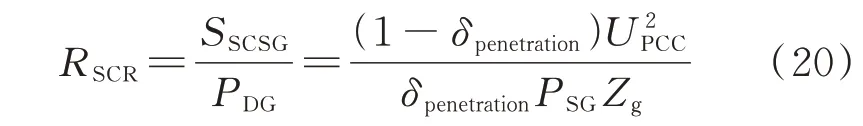
根据式（20）可知，电网强度主要与渗透率、网侧等效阻抗相关，其特性曲面见附录B 图B4。基于第1 章推导的阻抗模型，源网端发电容量变化对局部电网强网弱化特性的影响具体分析如下：

1）新能源渗透率提高。不同渗透率下逆变器阻抗Bode 图见附录B 图B5，随着逆变器并网容量的增加，其等效阻抗不断减小。由阻抗理论回比矩阵T=nYcsiZsg可知，等效于网侧等效阻抗增加，即等效电网强度随新能源渗透率的增加不断变弱。

2）网侧同步发电机发电容量降低。在“碳达峰、碳中和”需求下，随着新能源发电比例的提高，同步发电机发电容量逐渐降低，不同发电容量的同步发电机阻抗Bode 图见附录B 图B6。随着同步发电机发电容量的降低，其网侧阻抗在50 Hz 以下低频段的幅值不断增大，电网强度不断变弱。

基于以上源网端阻抗特性分析，随着新能源渗透率的提高，逆变器侧阻抗不断减小。同时，同步发电机容量的减小会导致网侧低频段阻抗不断增大，并网系统朝着电网强度弱化方向发展的同时，低频段源网阻抗易交互衍生低频失稳现象。由于柴油同步发电组具有P-f下垂特性，功率的低频振荡会间接导致基波频率发生波动，减弱系统频率维持能力，出现功率低频振荡耦合频率周期性波动的低频失稳现象。

2.2 强网弱化后衍生低频振荡频率失稳分析

为深入揭示该系统低频失稳机理并进行稳定性预判，基于第1 章所建立含基波频率扰动的阻抗模型，构建如图2 所示涵盖阻抗外特性与基频扰动特性的新能源主导发电系统模型框架。图中：Δisg为同步发电机定子电流小信号扰动量；Δv为同步发电机端口电压参考值小信号扰动量；ΔPref为有功功率参考值小信号扰动量；Δ为控制坐标系下逆变器输出电流小信号扰动量，Δ为其参考值。

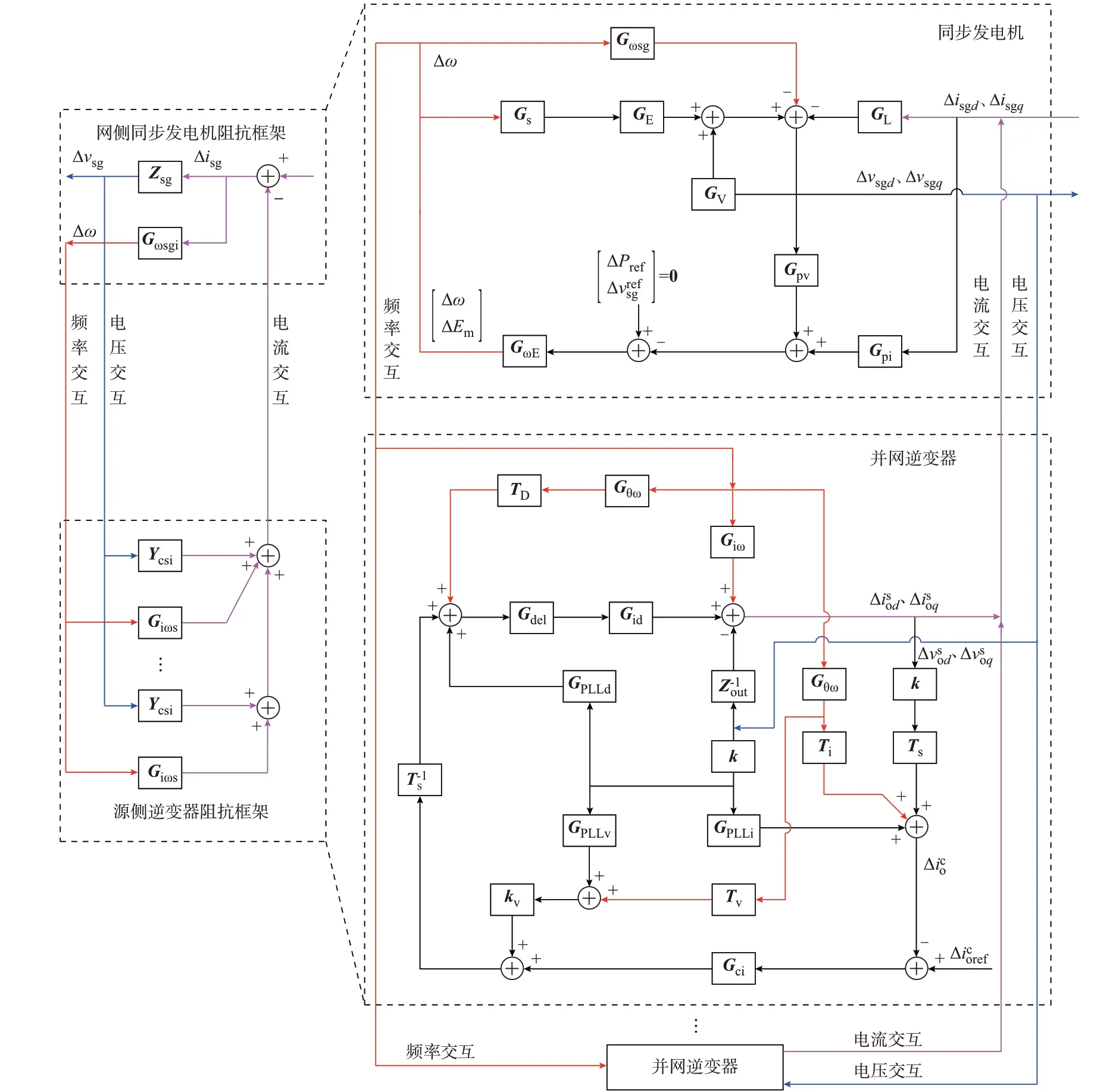
图2 含基频扰动的小信号模型框图Fig.2 Block diagram of small-signal model with fundamental frequency disturbance

与传统基于固定频率点的小信号阻抗分析框架相比，除电压、电流扰动回路外还包含红线所示频率扰动回路，且各扰动相互耦合，其具体耦合回路说明见附录A。根据图2 推导了涵盖系统电压、电流、频率扰动特性的特征方程，其中，同步发电机和新能源逆变器组网系统中电网电流对并网电压及系统频率扰动回路可简化为如附录B 图B7 所示前馈通道为I的负反馈闭环结构，且图B7（a）中系统阻抗特性与图B7（b）中频率特性反馈通道的表达式一致。

因此，基于广义Nyquist 判据，若要判断附录B图B7 所示并网系统稳定性，仅需判断式（21）所示含频率特性项回比矩阵的稳定性即可。即回比矩阵L的两个特征根Nyquist 曲线均不穿越(-1，j0)点，则系统稳定；回比矩阵L的任一特征根Nyquist 曲线穿越(-1，j0)点，则系统不稳定。同时，根据文献［20-21］可知，回比矩阵特征根Nyquist 曲线穿越(-1，j0)点的部分和负实轴交点处的频率与该系统位于右半平面闭环极点虚部的频率相对应，根据该对应关系可预判系统潜在失稳的振荡频率。

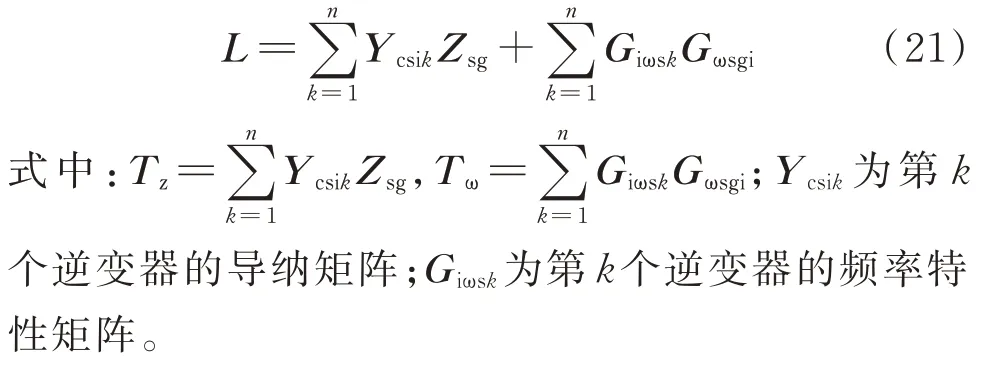
相比于基于固定频率点的回比矩阵，式（21）所示回比矩阵L阻抗特性项Tz引入了含频率扰动的部分动态矩阵Gωsg；并且L中新增加了频率特性项Tω，以全面表征电压、电流、频率扰动的交互回路特性。其中，Gωsg对阻抗特性项Tz的影响如附录B 图B8 所示，频率扰动的引入会导致阻抗特性项Tz在0.1～10 Hz 频段的幅频特性稍有下降，影响较小。探究频率特性项Tω的引入对回比矩阵L的影响，绘制如图3 所示考虑频率特性项Tω影响下回比矩阵L的Bode 图。可以看出，随着频率特性项Tω的引入，各轴幅频特性及qd、qq轴相频特性在0.1～4 Hz 频段均有下降，即新引入的频率特性项Tω主要影响系统模型的低频带特性。综上，频率扰动特性主要由回比矩阵L中的频率特性项Tω体现。

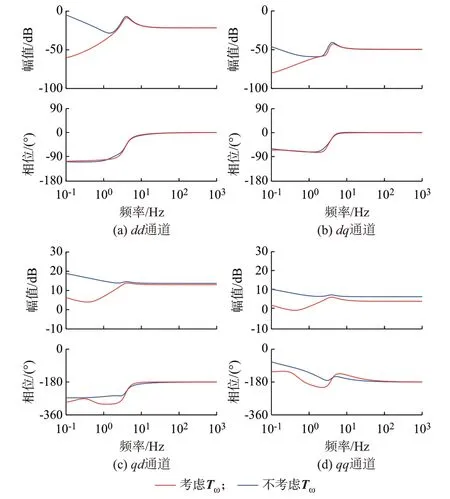
图3 考虑Tω影响的回比矩阵L 的Bode 图Fig.3 Bode diagram of return ratio matrix L considering influence of Tω

更进一步，分析不同渗透率下频率特性项Tω的特性变化，以揭示渗透率提高后系统低频失稳机理。不同工况下频率特性项Tω的Bode 图如图4 所示。可以看出，随着渗透率的提高，频率特性项的Bode 图幅频特性幅值不断减小，即开环增益的减小会导致环路控制的稳态精度下降，其控制特性将会变弱，频率回路的响应特性将会随之发生变化。随着局部电网内新能源发电渗透率的提高，系统调频容量及频率维持能力逐渐降低，低稳态精度控制特性下的频率扰动在电网强度弱化后的源网端低频段阻抗变化及频率、电压、电流扰动耦合的动态交互中可能造成扰动放大，进而导致系统低频失稳。

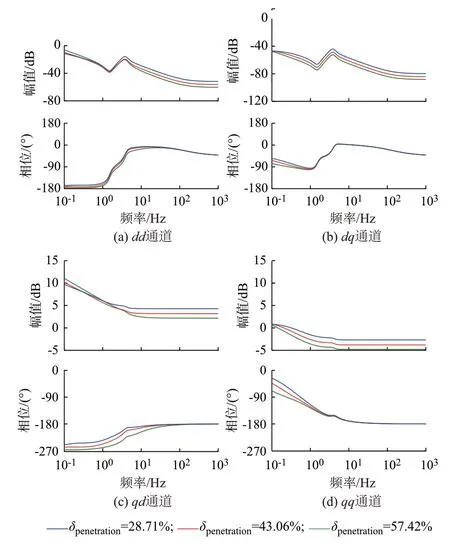
图4 不同渗透率下Tω的Bode 图Fig.4 Bode diagram of Tω with different penetration rates

基于式（21）定义的回比矩阵，应用广义Nyquist判据具体预判650 kW 区域电网在不同渗透率下的系统稳定性，系统参数见附录C 表C1 和表C2。

不同新能源逆变器并网数量下的回比矩阵特征根轨迹见附录B 图B9（a）至（c）。随着逆变器并网数量由2 台增加至4 台，即渗透率由28.71%提高至57.42%，回比矩阵L的两个特征根λ1和λ2的Nyquist曲线均不包围(-1，j0)点，表征系统可稳定运行。但回比矩阵特征根λ1的Nyquist 曲线逐渐趋于(-1，j0)点，即随着渗透率的提高，系统朝稳定性变弱的方向发展。

继续提高新能源渗透率，逆变器并网数量增加至5 台时，PDG=466.5 kW、PSG=183.5 kW、渗透率δpenetration=71.77%，附录B 图B10 所示回比矩阵L的特征根λ1的Nyquist 曲线包围(-1，j0)点，系统不稳定，存在低频失稳现象。且根据MATLAB 绘制的Nyquist 曲线与负实轴的交点频率为1.6 Hz，即预判该工况下系统将产生1.6 Hz 的低频振荡。

3 硬件在环实验验证与预判方法讨论

3.1 硬件在环实验

为了验证前文稳定性预判的正确性，在实时数字仿真器（RTDS）中搭建了如附录B 图B11 所示同步发电机与新能源并网逆变器组网的单母线型新能源主导局部电网验证平台，通过DSP28379 芯片实现逆变器控制与RTDS 功率部分采样与控制信号传输，参数见附录C 表C1 和表C2。

附录B 图B12 所示为不同渗透率下并网点电压、频率及各逆变器输出电流波形。图B12（a）中，新能源逆变器并网数量n=2、渗透率δpenetration=28.71%时，各逆变器输出电流均跟随200 A 给定，与并网点电压均具有较好正弦性，频率波动范围为49.995～50.005 Hz。图B12（b）中，n=3、δpenetration=43.06%时，各逆变器输出电流与并网点电压均呈现较好的正弦性，频率波动范围为49.99～50.01 Hz。图B12（c）中，继续增加逆变器并网数量至4 台、渗透率提高至57.42%时，各逆变器输出电流与并网点电压呈现良好的正弦性，但频率波动范围增大至49.9～50.1 Hz。由以上实验结果可以看出，随着渗透率的提高，系统虽可稳定运行，但基频波动逐渐变大。

继续提高新能源渗透率，当新能源逆变器并网数量n=5、渗透率δpenetration=71.77% 时，并网点电压、频率及各逆变器输出电流波形见附录B 图B13。由实验波形可以看出，随着新能源渗透率的提高，各逆变器输出电流与并网点电压均出现约1.79 Hz 的低频振荡，由于柴油同步发电机组的P-f下垂特性及同步发电机逆变器系统电压、电流、频率控制特性的耦合交互，低频振荡产生的同时导致频率也出现了同样的周期性波动，其波动范围最大达48～56 Hz，系统不能稳定运行，存在低频失稳现象。

3.2 稳定性预判方法讨论

结合2.2 节理论分析与3.1 节实验结果，验证了含基频扰动模型预判低调频容量高比例新能源主导局部电网低频失稳的可行性。为体现阻抗模型频率扰动加入的必要性及意义，结合3.1 节实验结果，将本文所提稳定性预判方法与传统基于定频阻抗模型的稳定性预判方法进行对比讨论。

根据图2 所示柴油同步发电机组与逆变器的小信号系统框图，仅考虑传统电压与电流扰动回路，可推导出用于稳定性预判的传统回比矩阵Lvi，如式（22）所示。相比于式（21）所示含基频扰动的回比矩阵L，Lvi仅包含传统阻抗特性项，不含具有频率扰动特征的部分动态矩阵Gωsg及频率特性项Tω。

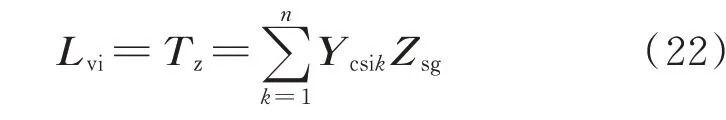
在与2.2 节相同工况下，绘制式（22）所示传统回比矩阵Lvi特征根的Nyquist 曲线进行稳定性预判，见附录B 图B14。可以看出，随着渗透率的提高，传统回比矩阵Lvi两个特征根的Nyquist 曲线趋于(-1，j0)点但并未包围，表征系统稳定性在向变弱方向发展。但在逆变器并网数量为5 台、渗透率δpenetration=71.77%的失稳实验工况下，采用该方法预判系统仍可稳定运行。因此，采用仅考虑电压、电流扰动的传统回比矩阵在该临界失稳工况下的稳定性预判结果与附录B 图B13 所示实验现象不符。

根据3.1 节实验结果，在渗透率δpenetration=71.77%的临界失稳工况下，绘制如图5 所示传统回比矩阵Lvi与考虑基频扰动回比矩阵L特征根λ1的Nyquist 曲线进行对比分析。对比可知：基于传统回比矩阵预判系统稳定性，回比矩阵特征根λ1的Nyquist 曲线不包围(-1，j0)点，表征系统可稳定运行；而应用本文所提考虑基频扰动的回比矩阵预判系统稳定性，回比矩阵特征根λ1的Nyquist 曲线包围(-1，j0)点，且根据MATLAB 绘制的Nyquist 曲线与负实轴的交点频率可预判该工况下系统潜在1.6 Hz 的低频振荡，稳定性预判结果与附录B 图B13所示临界工况实验现象基本相符。

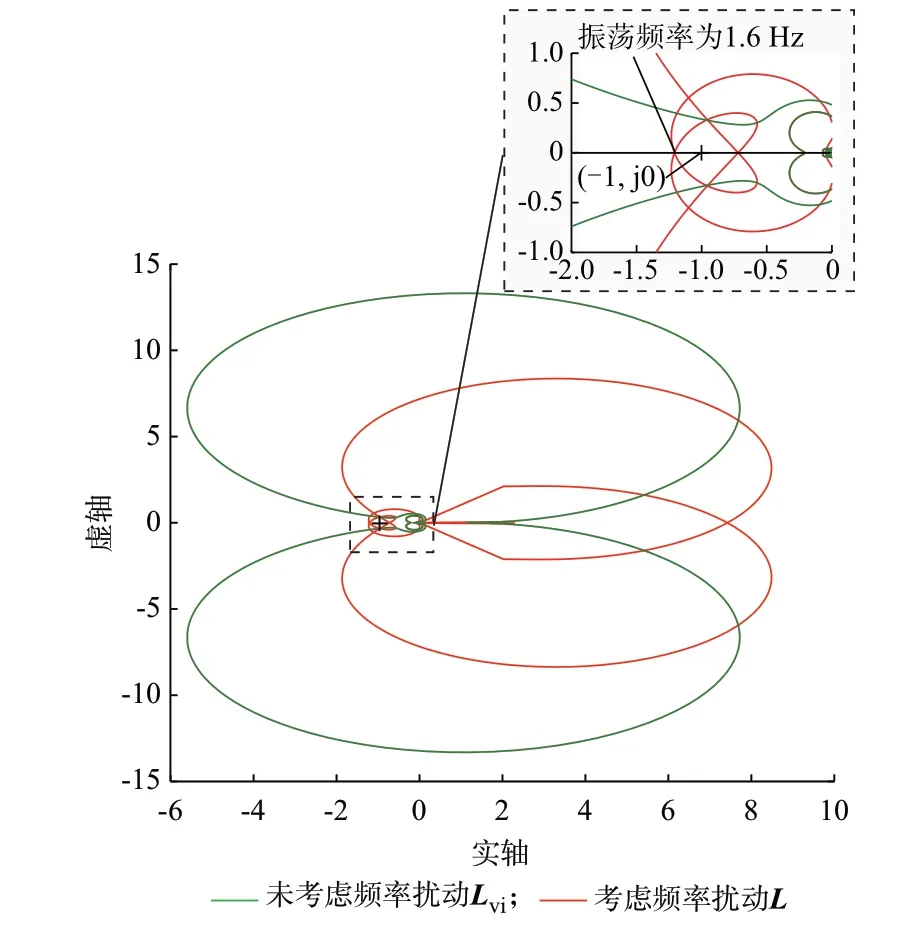
图5 临界失稳工况下不同回比矩阵特征根λ1的Nyquist 曲线Fig.5 Nyquist curves of λ1 with different return ratio matrixes under critical instability condition

根据以上对比分析可知，仅考虑电压、电流扰动的传统定频阻抗模型在分析高比例新能源发电系统强网弱化后衍生的低频失稳问题时适用性较差，不能准确预判系统潜在的低频失稳问题。而本文所研究的考虑基频扰动，涵盖基频扰动特征的阻抗模型可更准确地预判系统的低频失稳问题。

4 结语

为有效分析局部电网内新能源发电比例提高、调频容量降低后系统潜在的低频振荡现象，本文将基波频率扰动作为新一维扰动量引入现有基于固定基波频率阻抗研究框架中，通过建立柴油同步发电机组、并网逆变器的变频阻抗模型，构建了除电压、电流扰动外含基波频率扰动回路覆盖系统阻抗外特性及基频响应特性的新能源主导发电系统模型框架。基于同步发电机及逆变器阻抗外特性，从新能源渗透率提高、网侧同步发电机容量降低的角度分析网侧低频段阻抗不断增大、低频段源网阻抗易交互发生低频振荡频率失稳的诱因。通过所构建的含基频扰动特征的回比矩阵，从频率特性角度分析了高渗透率下频率特性项低稳态精度控制及扰动环路耦合对系统低频失稳的影响，且预判了不同渗透率下系统稳定情况及潜在失稳频带。并在实验结果中以临界不稳定工况为背景对比分析含基频扰动模型与传统定频模型对低频失稳预判的适用性，含基频扰动阻抗模型相比于传统定频阻抗模型可准确预判高比例新能源发电系统强网弱化后衍生的低频振荡频率失稳，为后续高比例新能源低频振荡频率失稳机理分析及治理提供了新的建模思路。下一步工作将应用该阻抗分析框架深入分析多频带失稳问题。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。