计及车-路-站-网融合的电动汽车充电负荷时空分布预测

刘志强，张 谦，朱 熠，吴佳琦，黄耀宇，李春燕

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆市 400044；2. 国网重庆市电力公司綦南供电分公司，重庆市 401420）

0 引言

在“碳中和、碳达峰”目标引领下，以清洁能源为动力的电动汽车（electric vehicle，EV）快速发展。EV 保有量增加对于中国实现“30·60”双碳目标、推动环境可持续发展、打造环境友好的生态圈具有巨大的意义［1］。但大规模EV 无序接入，将给电力系统带来负荷增长［2］、电能质量下降［3］、电网运行优化控制难度增加［4］等不利影响，对充电站规划提出越来越高的要求。现有研究常通过有序充电控制解决上述问题，而有序充电控制以EV 充电需求时空分布的准确预测为基础。

目前，EV 充电负荷时空分布研究主要从EV 运行规律出发［5］，结合出行链［6］和用户意愿［7］开展。文献［8］从用户行驶规律出发，通过拟合用户出行链特征量来计算区域内充电需求。文献［9］运用最短路径算法选择耗时最短的行驶路径，采用蒙特卡洛方法模拟区域交通路网和出行链，计算EV 可响应功率和容量。文献［10］通过模糊推理建立用户参与充放电调控的意愿模型，并计算考虑EV 用户参与意愿度下的实际调控能力水平。但是此类文献鲜有关注实时动态交通流变化导致的能耗改变。另一方面，目前的研究大多直接以区域内的EV 保有量作为出行量［11］，然而天气类型、环境温度等外部因素将会影响用户出行意愿，实际出行EV 数量与EV 保有量有一定偏差。因此，计及用户出行意愿的EV出行数量和出行链修正在研究EV 充电负荷时空分布时不可忽视。

同时，虽有文献对影响EV 充电行为的多种潜在因素进行了研究［12］，但对区域内充电站位置不同导致EV 行驶轨迹的变化，进而改变荷电状态（state of charge，SOC）的时空分布的研究较少。文献［13］研究了不同日期下用户充电行为习惯，得到了用户出行目的与日期类型的关联性。文献［14］从客观因素，如距离、行驶速度等来确定用户对EV 充电站的选择，却忽略了用户的主观意愿，如充电站的规模、排队时间等对用户选择的潜在影响。此外，还有学者从出行路径［15］和充电地点［16］选择的角度研究了其对EV 充电负荷的空间分布影响，但大多数研究未考虑大规模用户对不同位置充电站的选择导致EV 荷电状态时空分布的变化。

针对以上研究的不足，本文考虑了区域内道路拥堵情况和环境温度等因素对EV 能耗和用户出行意愿的影响，建立了EV 与路网融合的单位里程能耗模型和出行链修正模型；进一步，计及多个充电站对用户行驶路径选择的影响，以及大规模EV 充电站选择的相互影响，基于传统的万有引力模型，建立了EV 与充电站融合的充电站选择模型；最终，基于起点-目的地（OD）矩阵和准动态交通流模型，模拟了路网中EV 的出行行为和充电选择，实现了计及车-路-站-网多方信息融合下的EV 充电负荷时空分布预测。

1 外部环境对EV 能耗的影响

EV 单位里程能耗是计算车-路-站-网多方融合下的EV 负荷时空分布的基础，而环境温度及交通拥堵情况对EV 单位里程耗电量的影响最大［17］。

1.1 温度对EV 能耗的影响

1.1.1 温度对电池的影响

不同的环境温度会影响EV 的充放电效率，文献［18］对动力电池系统的研究发现，在一定温度范围内，随环境温度升高，动力电池系统能量效率增大。通过文献中实验数据可得温度和EV 充放电效率曲线如附录A 图A1 所示，曲线拟合所得关系式为：

式中：T为环境温度；η为EV 电池充放电效率。

1.1.2 环境温度对EV 空调开启的影响

在不同的环境温度下，用户开启车内空调的时间长度不同，文献［19］通过对汽车空调开启的数据进行统计测试，拟合出空调开启率的计算公式，得到不同温度下的空调开启率与环境温度的关系如式（2）所示。文献［17］定义了温度能耗系数，通过拟合实际数据得到其与温度的非线性关系，以及与空调开启时耗电量的比值关系，如式（3）所示，其函数关系图见附录A 图A2。

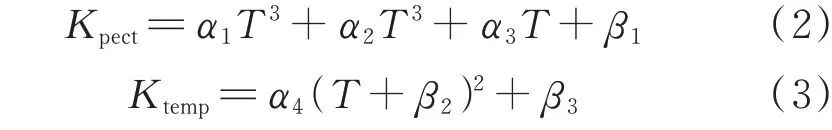
式中：Kpect为不同温度下的空调开启率；Ktemp为温度能耗系数；α1～α4与β1～β3为拟合系数。

1.2 交通对EV 能耗的影响

不同的交通拥堵情况下，EV 的行驶路径以及行驶速度不同，能耗也不一样。文献［20］给出了城市各级道路的行驶速度区间，如表1 所示。

表1 不同道路等级和拥堵程度下的行驶速度区间Table 1 Driving speed range with different road classes and congestion levels

同时，文献［21］通过实测数据对单位能耗与行驶速度之间的关系进行拟合，如式（4）所示。

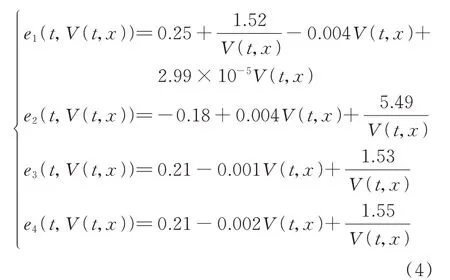
式中：eh（t，V（t，x））为不同道路等级的单位耗电量；h=1、2、3、4 分别表示快速道、主干道、次干道、支干道；V（t，x）为t时刻x位置上EV 的速度。

1.3 EV 单位里程能耗计算

基于上述单位能耗与行驶速度关系式，考虑电池充放电效率与空调开启时的温度能耗系数对单位里程能耗的影响，EV 空调开启时的单位里程能耗如式（5）所示。

式中：e（t，x，T）为t时刻处于位置x、环境温度为T时的EV 单位里程能耗。

根据上述公式，可得到温度与行驶速度变化下单位里程能耗曲线，如附录A 图A3 的主干道中能耗随速度和温度变化曲线所示。

2 计及用户出行意愿的出行链修正

现有文献常基于传统出行链进行研究，未计及用户主观意愿对出行链的影响。本章从人体舒适度理论出发，实现对传统出行链的修正。

2.1 传统EV 出行链模型

EV 主要分为私家车、公交车以及出租车，本文主要研究私家车的荷电状态时空分布。电动私家车的主要出行行为及各活动行程所占比例［22］设定如表2 所示。出行目的地可分为家庭、公司、商场、休闲场所和其他地点5 个类型，分别简写为H、W、SE、SR、O。

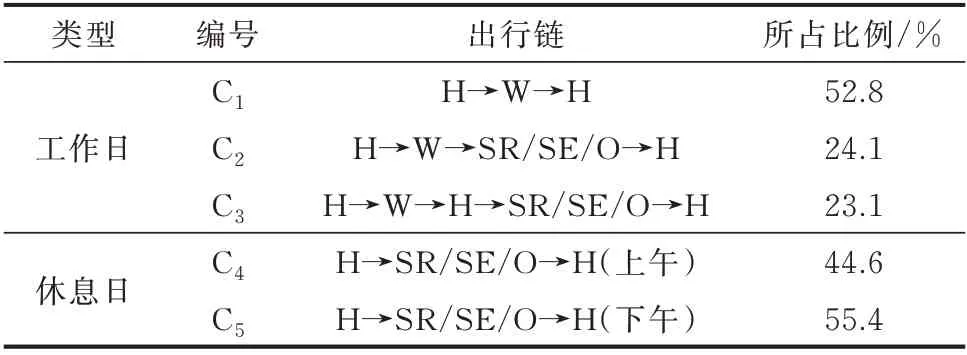
表2 传统的电动私家车出行链Table 2 Trip chain of traditional electric private car

每一条出行链可以分解为多个“出行段”，每个出行段开始时间ts服从如式（6）所示的正态分布。

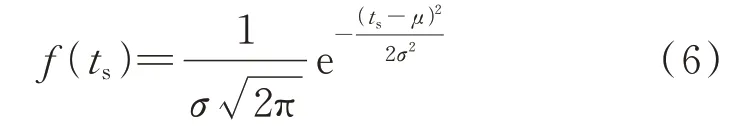
式中：μ和σ分别为不同出行链对应开始时刻的均值与方差，具体参数如附录B 表B1 所示［23］。

2.2 计及外部环境的用户出行意愿研究

本文选用人体舒适度标准描述外部环境对用户出行意愿的影响。人体舒适度指数常采用预测平均指数（predicted mean vote，PMV）和预测不满意比例（predicted percentage of dissatisfied，PPD）这两项指标描述［24］。PMV 是预计平均温度感觉指数，分别用-3、-2、-1、0、+1、+2、+3 表示冷、凉、微凉、舒适、微暖、暖和、热，如式（7）所示。

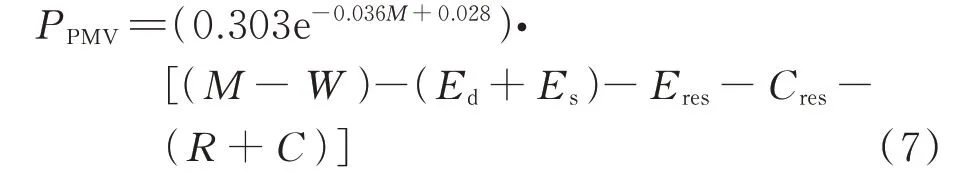
式中：PPMV为PMV 数值；M为人体代谢率；W为有效机械功率；Ed为汗液散热；Es为蒸发散热；Eres为潜在散热；Cres为可感散热；R为辐射散热；C为对流散热。上述参数计算公式见附录C 式（C1）至式（C10）。

PPD 是定量预测感觉太冷或太热的不满意率的指数，可通过拟合式（8）计算PPD 数值：

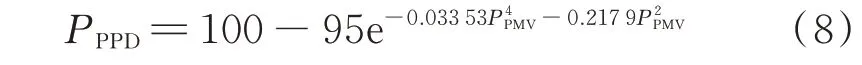
2.3 基于用户出行意愿的出行链修正

基于上述人体舒适度指数标准，定义EV 用户的出行意愿如式（9）所示。

工作日的EV 出行数量受外部条件影响甚小，主要变化在于用户下班后选择回家或继续出行［25］。根据用户出行意愿，传统出行链C2（24.1%）的用户只有在感觉气温舒适时才会选择继续出行，故将其修正为24.1%P。此外，C2修正前后差值中会有部分人选择先回家再出行，故对传统出行链C1和C3进行修正，结果如表3 所示。同理，对休息日的EV 出行链进行修正，结果如表4 所示。表中：P1、P2、P3分别为工作日、休息日上午和下午EV 用户的出行意愿。基于此，便得到了基于用户出行意愿的EV 出行链修正。

表3 工作日下计及用户出行意愿的出行链Table 3 Trip chain considering users’travel intention in working days

表4 休息日下计及用户出行意愿的出行链修正Table 4 Trip chain considering users’travel intention in rest days

3 基于万有引力模型的EV 充电站选择模型建立

随着EV 的发展，用户可通过充电站实时运营信息平台、APP 实现更多资源信息共享，同时不同用户之间的充电站选择可能会相互影响，进而导致EV 荷电状态时空分布发生变化。因此，本章基于万有引力模型，考虑充电站规模、排队等待时间、用户选择相互影响等因素对充电站选择的影响，以准确预测EV 荷电状态时空分布。

3.1 万有引力定律

万有引力模型常用来描述空间中两物体的相互作用规律。由于EV 对于充电站的选择受到多种因素的影响，且主观随机性较大，故可将其类比为用户与充电站之间的相互作用［26］。目前，万有引力模型已应用到多个领域以描述空间内物理量的相互作用，传统万有引力模型如式（10）所示。

式中：F12为天体间的万有引力大小；k为引力系数；M′为中心天体的质量；m为行星质量；r为中心天体和行星之间的距离。

3.2 基于充电站规模设施的中心天体质量类比

对充电站而言，其规模越大意味着充电桩的数量越多，对EV 的吸引力越大。单区域内各充电站的充电价格及充电桩型号基本相同，但充电桩的使用频率不同，导致其效率存在差异，这将直接影响EV 充电费用与时长，进而影响EV 对充电站的选择。因此，引入充电站内充电桩数量、效率来替代万有引力模型中的“中心天体质量”，如式（11）所示。

式中：Mj为充电站j的规模设施对EV 选择的影响，j=1，2，…，Ns，其中Ns为区域内总充电站数量；φj和µj分别为充电站j内充电桩数量和效率。

3.3 基于EV 荷电状态的行星天体质量类比

对EV 而言，当其荷电状态越低时，选择近距离充电站的意愿越强；反之，距离对用户选择的影响越弱。因此，本文引入EV 的荷电状态替代万有引力模型中的“行星天体质量”，如式（12）所示。

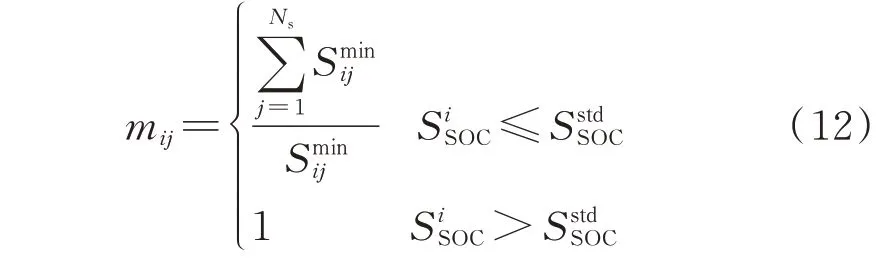
式中：mij表示第i辆EV 的荷电状态对EV 选择的影响，i=1，2，…，Ne，其中Ne为区域内总EV 数量；S为第i辆EV 与充电站j的最短距离；OC为第i辆EV 的荷电状态；S为EV 荷电状态阈值。当第i辆EV 的荷电状态大于SstdSOC时，mij取1，荷电状态对EV 选择无影响；反之，mij等于第i辆EV 距离各个充电站最短路程之和与其距离充电站j的最短路程的比值，即第i辆EV 与充电站j相对其余充电站越近，充电站j的吸引力越强。

3.4 计及多路径的充电站距离测度计算

现有物流研究通过运输距离、时间等描述空间中两点之间的综合距离。借鉴物流中计算综合距离的思想，本文在进行充电站选择时，选取两地间多条主要路径的长度和该路径行驶耗时为指标，确定两地的综合距离，如式（13）所示。

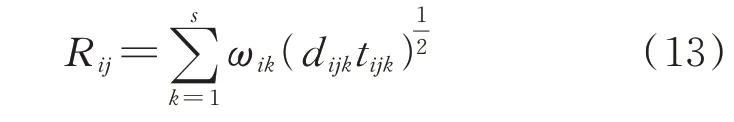
式中：Rij为第i辆EV 与充电站j之间的综合距离；s为两地之间主要路径数；ωik为第i辆EV 采用第k条路径的权重，可通过路网中车辆在该路径行驶次数与所有路径行驶次数的比值确定；dijk为第i辆EV 采用第k条路径前往充电站j的距离；tijk为第i辆EV 采用第k条路径前往充电站j的耗时，其值等于EV 选择第k种路径上的耗时troad，k，即

3.5 引力系数类比

区域中存在多个充电站时，某些充电设施完善或规模较好的充电站会因为较多EV 选择，而出现可用充电桩数量较少、排队时间增长导致其对EV用户吸引力下降的现象。同时，其余的充电站会因为前者吸引力下降，而出现吸引力上升的情况，即充电站集群会因EV 集群选择而产生不对称性。因此，可定义引力系数用以调整多个充电站因EV 选择造成的不对称性的系数。

引入自引力系数和互引力系数，其中自引力系数用以描述充电站未满载时，EV 选择对充电站吸引力的影响程度，通过充电站内在站充电的EV 数量定义，并归一化处理，如式（15）所示。当充电站j未满载运行时，在站内充电的EV 数量越少，自引力系数越大，即充电站j对第i辆EV 吸引力增大。

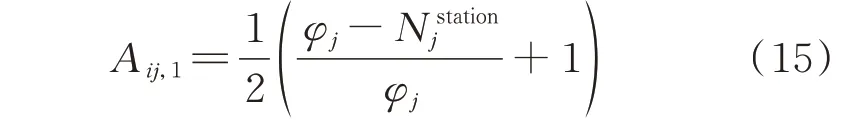
式中：Aij，1为充电站j对第i辆EV 的自引力系数；Nstationj为充电站j内在站充电的EV 数量，0 ≤Nstationj＜φj。

互引力系数用以描述充电站满载情况下，EV选择对充电站吸引力的影响程度，通过充电站的EV 排队数量定义，并归一化处理。因为多个充电站的EV 排队数量对吸引力影响是相互的，可通过计算充电站j内EV 排队数量占充电站集群排队数量总和的比例来描述，呈负相关，即当充电站j排队数量占比越大，则互引力系数越小，充电站j对第i辆EV 吸引力减小，如式（16）所示。

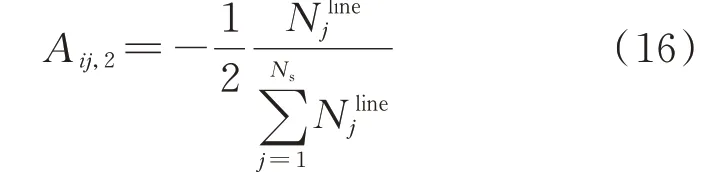
式中：Nlinej为充电站j的EV 排队数量；Aij，2为充电站j对第i辆EV 的互引力系数。

综上，由于引力系数不能为0，定义充电站j与第i辆EV 之间的引力系数kij，如式（17）所示。

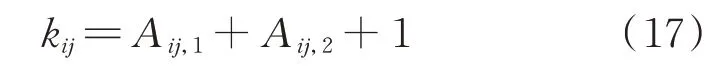
根据充电站内在站充电的EV 数量和EV 排队数量将引力系数分为未满载和满载两种情况：（1）当充电站未满载时，其互引力系数为0，引力系数等于自引力系数，kij∈（1.5，2］；（2）当充电站满载时，自引力系数为0.5，互引力系数Aij，2∈［-0.5，0］，使得kij∈[1，1.5]。故第i辆EV 与充电站j之间引力Fij类比的万有引力模型如式（18）所示。

基于此，可逆向分析不同位置充放电站对EV选择的影响，进而计算EV 充电负荷的时空分布。

4 EV 充电负荷计算模型建立

EV 充电负荷的时空分布与其行驶路径密切相关。本章结合第2 章修正后出行链和准动态交通流法［27］以获得EV 非充电行驶路径选择，从而模拟EV在各时刻的位置；当EV 产生充电需求时，基于第3章中充电站选择模型确定EV 的充电目的地；基于第1 章中EV 单位里程能耗，最终确定EV 充电负荷的时空分布。

4.1 OD 矩阵

在交通领域通常用OD 矩阵来描述交通流量的特征和变化，其形式如式（19）所示。

矩阵中的每一个元素表示两节点之间的交通量，其中该元素所处的行和列就分别表示起讫点的编号，如oab表示从节点a出发到节点b的交通量。

将2.1 节中EV 出行链分为多个出行段（（如表2中出行链C1可分为出行段c11、c12，分别表示H→W和W→H）），定义出行段cwv的OD 矩阵为Owv，以各道路设计通行流量为标准，见附录B 表B2，计算Owv。一天中多个出行段Owv矩阵之和等于该区域内总OD 矩阵，即

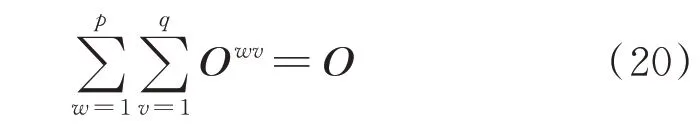
式中：q为出行段数量；p为出行链数量。

4.2 交通阻抗函数

为合理分配上述矩阵Owv中交通量，并计算EV在路网中的通行时间，通过美国公路局阻抗模型计算路阻，如式（21）所示。

式中：ta为路段a的通行时间即交通阻抗；ca为在交通规划阶段，路段a的初始设计通行流量；qa为路段a的交通量；t0为交通松弛状态的通行时间；α、β为固定参数。

4.3 基于OD 矩阵的准动态交通流模拟

基于上述OD 矩阵，通过准动态交通流法，实现以最短路径进行分时段的交通量增量分配。首先，通过各出行段出发时间概率密度曲线对各出行段OD 矩阵进行时间区间划分为N个时段，按照时序依次分层分配到路网上；其次，每一层采用最短路径法分配，同步修正路阻函数，直到N层OD 矩阵全部分配完毕；最后，考虑每一段时间都会有OD 矩阵进入或退出的情况进行出行量校正。因此，路网中任一时段和路段的交通量为：

由此，一天内任意时刻的道路阻抗情况以及交通流情况都能够获得，即可实现一天内的交通情况模拟。

4.4 EV 充电负荷计算

通过蒙特卡洛抽样获取EV 初始荷电状态，结合单位里程能耗ei（t，x，T），第i辆EV 的荷电状态等于出行段开始时EV 剩余电量减去行驶消耗电量，如式（23）所示。

式中：Ei为第i辆EV 当前剩余电量；E′i为第i辆EV初始剩余电量；L为途经路段长度。

以EV 当前位置为初始点，若Ei无法满足行驶到下一个目的地时，则触发充电需求，其判断条件如式（24）所示。

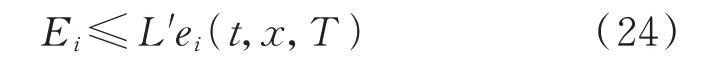
式中：L′为车辆当前位置到下一目的地的路程。根据式（24），当EV 产生充电需求时，基于充电站选择模型确定充电目的地，进而计算EV 充电负荷的时空分布。综上，本文方法整体架构如附录A 图A4所示。

5 算例分析

5.1 参数设置

本文以附录A 图A5 所示规划区域为例进行仿真测试。该区域大小为18.8 km×9.7 km，包含19 个区域、17 个节点及33 条道路。其中，不同虚线颜色对应不同类型区域，棕色表示工业区，黄色表示居民区，蓝色表示商业区，绿色表示绿化区，红色表示不可规划区域。不同道路颜色表示不同道路等级。

为充分考虑区域路网中多辆EV 的相互影响对充电站选择的影响，本文暂不考虑通过私人充电桩充电，只考虑用户在充电站充电。假设区域内充电设备集中在节点2、节点7、节点15，其可用充电桩的数量分别为105、120、150。各节点间的距离见附录B 表B3。常温周一周内上午、下午、晚上平均温度见附录B 表B4。路网中EV 保有量为4 500。

5.2 出行链修正结果分析

根据第2 章可以得到PMV、PPD 和满意度如附录B 表B5 至表B7 所示。从而得到常温周用户出行链修正结果，此处只列举部分时段的出行链修正结果，如表5 所示。

由表5 可知，工作日出行链修正前后，C2出行链比例减少，C1、C3出行链比例增加；休息日出行链修正前后，实际出行数量较修正前有减少。综上，修正后的出行链考虑了用户的主观意愿，弥补了传统出行链直接将EV 保有量作为EV 出行数量导致负荷预测不准确的不足。

表5 常温周内部分时段出行链修正结果Table 5 Correction results of trip chain of some time periods in normal-temperature week

5.3 基于万有引力模型的充电站选择仿真分析

为验证本文所提基于万有引力的充电站选择模型的有效性，分析EV 用户选择充电站时的相互影响，本文设置以下3 个仿真场景进行分析：

仿真场景1：不考虑充电站吸引力，EV 用户以最短距离选择充电站。

仿真场景2：考虑充电站吸引力，但不计及多辆EV 间的相互影响，用户仅考虑充电站规模设施、综合距离以及自身荷电状态选择充电站。

仿真场景3：考虑充电站吸引力，计及多辆EV选择相互影响，用户能够通过充电站获得全局信息。

5.3.1 考虑万有引力模型的充电站选择仿真结果分析

在场景2 下进行仿真分析，EV 用户在不考虑相互影响的情况下，仅以充电站规模设施、综合距离长短以及自身荷电状态来选择充电站，选取节点6、9、12 处的3 辆EV 仿真结果如表6 所示，详细结果见附录B 表B8，充电站的选择以及路径选择如图1所示。

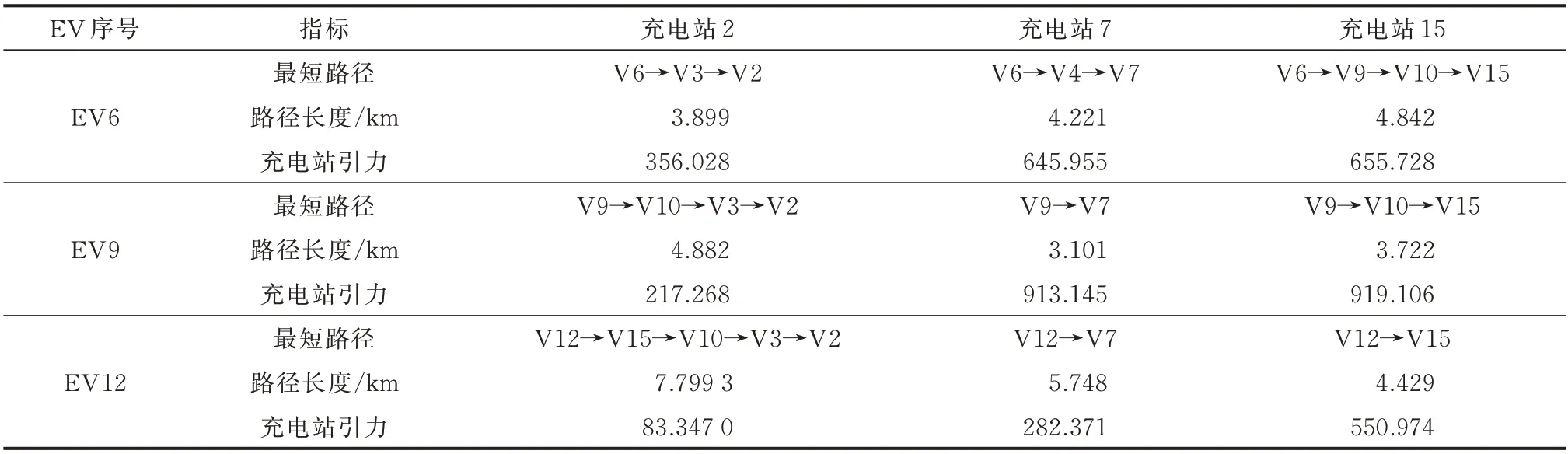
表6 场景1 与场景2 的EV 充电站选择结果对比Table 6 Comparison of EV charging station selections in scenario 1 and scenario 2

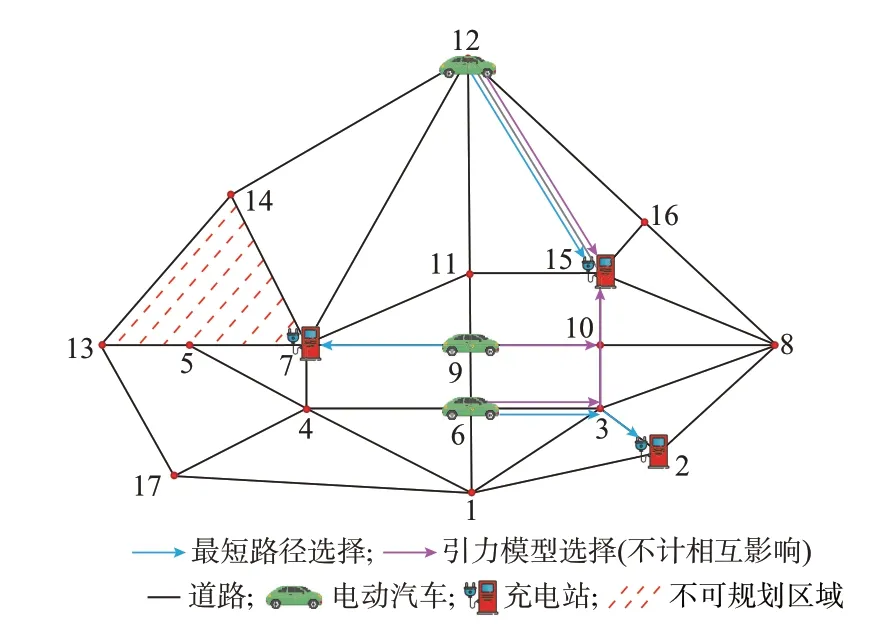
图1 场景1 与场景2 的充电站选择Fig.1 Charging station selection in scenario 1 and scenario 2

由表6 和图1 可知，EV6、EV9、EV12 最终均选择了充电站15。而在场景1 的情况下，EV 仅考虑距离最近的充电站进行充电，由表6 中EV 距离各充电站最短路径可知，EV6、EV9、EV12 的选择分别为充电站2、7、15。

以EV6 为例，虽然其到充电站2 的路径长度最短，但在考虑了充电站规模设施、综合距离下的路径拥堵以及自身荷电状态等因素选择后，EV6 与充电站7 的引力为655.728，高于其与充电站2 的引力356.028，故用户选择了距离稍远的充电站7 进行充电。同理，EV9 和EV12 考虑了充电站信息和自身情况后，选择充电站7 和充电站15。

综上，在不考虑EV 间相互影响的情况下，基于万有引力的充电站选择模型能够量化路网拥堵情况、充电站信息和用户自身情况对充电站选择的影响，并做出更为合理的选择，修正以最短距离选择充电站带来的偏差。

5.3.2 考虑EV 间相互影响的充电站选择仿真结果分析

在场景2 中，不计及用户相互影响的万有引力选择模型虽然能够修正用户以最短距离选择充电站带来的偏差，但是完全以充电桩数量、效率和用户荷电状态等因素考虑用户充电站选择并不全面。因此，在场景3 中，计及用户相互影响下进行仿真分析，其仿真结果如表7 所示，详细结果见附录B 表B9，充电站的选择以及路径选择如图2 所示。

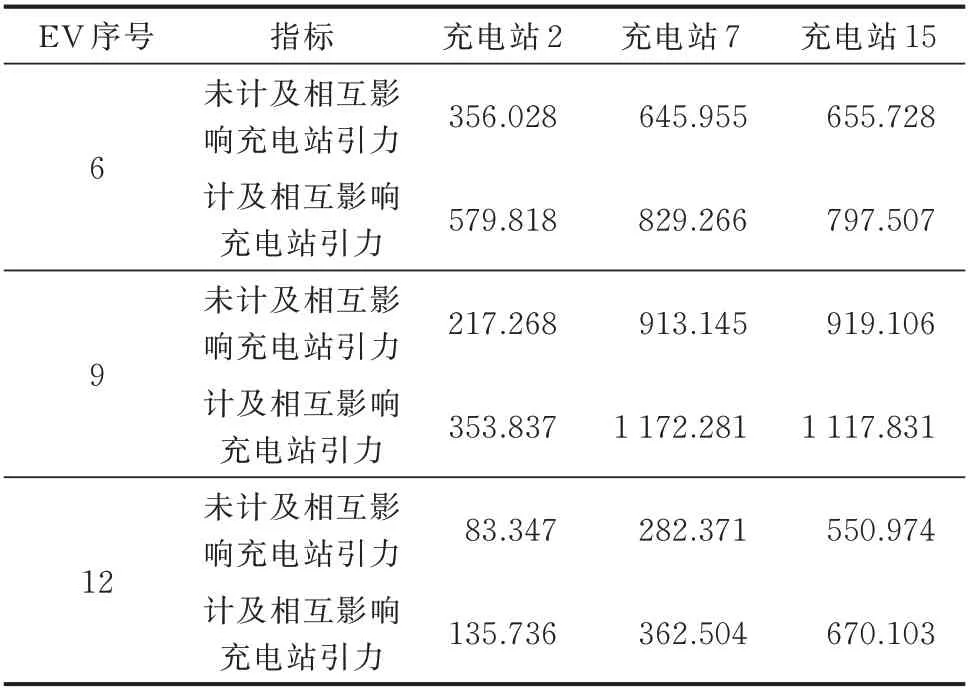
表7 场景2 与场景3 的EV 充电站选择结果对比Table 7 Comparison of EV charging station selection in case 2 and case 3

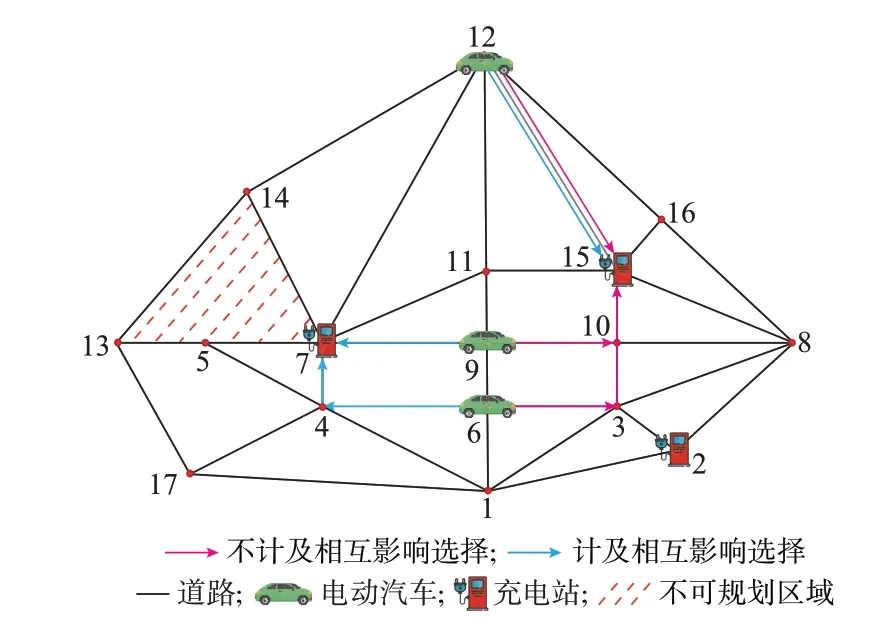
图2 场景2 与场景3 的充电站选择Fig.2 Charging station selection in case 2 and case 3

由表7 和图2 可知，由于区域内EV 的选择相互影响，导致充电站15 的排队EV 较多，从而充电站7对EV6 的吸引力由645.955 上升到829.266，高于其与充电站15 的引力797.507，故EV6 的选择由充电站15 变为充电站7。同理，EV9 的选择由充电站15变为充电站7，而EV12 选择不改变。因此，EV 集群选择会对充电站吸引力造成较大的影响，导致EV充电负荷时空分布发生变化，因此在研究EV 充电站选择时不可忽略多辆EV 的相互影响。

5.3.3 节点充电负荷对比分析

为进一步分析EV 用户充电站选择不同对节点充电负荷的影响，对比分析了同一工作日下节点15和节点7 在两种情景下的充电功率，结果如图3所示。

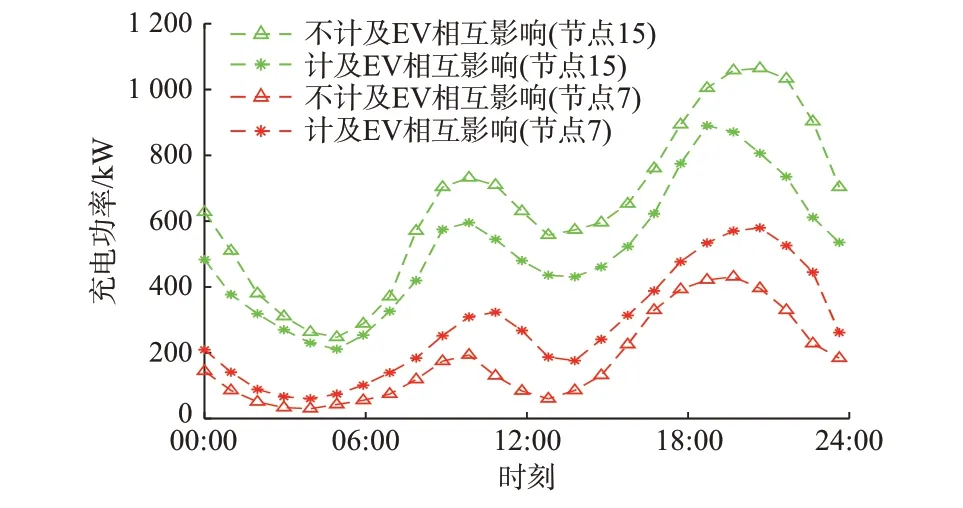
图3 节点15 与节点7 充电功率对比Fig.3 Comparison of charging power between node 15 and node 7

由图3 可知，在考虑了EV 用户相互影响情况下，节点15 整体充电功率下降，节点7 整体功率上升，特别是在高峰时段变化较大。这是由于充电站15 虽然规模更大和便利性更高，但在计及用户间的相互影响后，高峰时段大量EV 聚集在节点15 充电导致交通拥堵、排队时间增长，此时充电站15 吸引力降低，使得其部分负荷转移到节点7。仿真结果验证了基于万有引力的充电站选择模型能够计及用户厌恶拥堵和排队的心理，更准确测算不同位置充电站的充电负荷。

5.4 EV 充电负荷时空分布计算结果分析

将同一工作日下本文提出的计及车-路-站-网多方融合的区域内充电负荷预测结果与常规预测方法［28］以及基于马尔可夫决策过程（MDP）随机路径模拟的预测方法［29］进行对比，仿真参数皆按照本文参数进行设置，仿真结果如图4 所示。

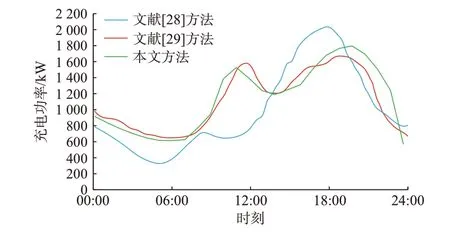
图4 工作日内区域充电功率Fig.4 Regional charging power in working days

由图4 可知，在计及车-路-站-网多方影响下，大部分EV 用户在08：00 左右开始活动，EV 电量降低，区域内充电功率开始上升，在11：00 左右上升至第1 个高峰。到14：00 左右充电功率再次明显地上升，在20：00 左右迎来一天中需求最高峰，之后再逐渐下降。一天内的负荷高峰集中在中午12：00 和晚上20：00 左右。

本文方法和文献［29］的充电功率曲线均在中午与下午时段出现了负荷高峰，而文献［28］仅在下午时段出现一个高峰。原因在于本文方法和文献［29］进行了动态路径模拟，用户在路网中的充电选择以及充电时间相对分散，而文献［28］是将充电时间固定为EV 位于各个场所时，因而相对集中。

对比文献［29］的充电负荷预测方法，在同一工作日内的需求变化趋势大致相同，但计及用户出行意愿的EV 充电负荷水平在白天时段略低，夜晚略高，需求高峰时段也出现了偏移。主要原因在于计及用户出行意愿后，修正了出行链中EV 数量，白天的出行比例降低，充电负荷减小，而夜晚用户的出行意愿增加，出现了更高的峰值。

为进一步分析各主要节点的负荷特性，选取同一工作日和休息日内节点2、节点7 和节点15 的充电负荷，如图5（a）和（b）所示。

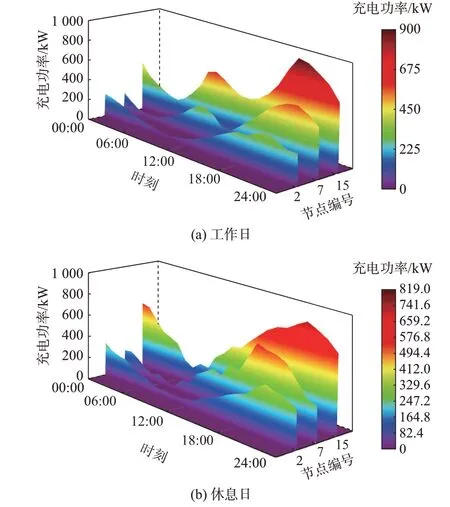
图5 休息日和工作日内节点充电功率对比Fig.5 Comparison of node charging power between rest days and working days

从仿真结果可看出，以工作日为例，节点15（充电功率为896 kW）和节点7（充电功率为581 kW）的峰值功率比节点2（充电功率为385 kW）分别高出132.7%和50.9%。这是由于节点15 和节点7 处在工业区、商业区和居民区交汇点，相比节点2 处在居民区中，充电需求用户更广。同时，由于节点15 充电站规模最大，其充电负荷最大。

以节点15 为例，在工作日内出现了双峰现象，充电负荷最高峰出现在20：00 时刻，一天内峰谷差为685 kW，双峰峰谷差为301 kW。而休息日内由于用户出行较晚，充电负荷高峰有所偏移，出现在21：00 时刻，且负荷集中在夜晚，从18：00 开始充电负荷都处于较高水平，负荷高峰为819 kW，日内峰谷差为665 kW。

6 结语

为准确测算区域内EV 充电负荷时空分布，本文计及EV、路网、充电站和电网多方因素，建立EV用户充电站选择模型，实现了区域内充电负荷时空分布预测，通过算例仿真可得到以下结论：

1）环境温度的变化会影响用户出行意愿，导致不同出行链EV 数量变化，本文所建立的出行链修正模型可解决将EV 保有量作为出行数量带来的测算偏差；

2）基于万有引力的充电站选择模型能有效刻画充电站规模、行驶距离、排队时间、交通拥堵以及EV 间相互影响导致的负荷时空分布变化，更准确地预测EV 充电负荷时空分布；

3）充电站规模及其位置对其充电负荷有较大影响，本文从EV 用户角度，逆向分析不同位置充电站对EV 荷电状态时空分布的影响，可为EV 有序充电策略、充电站规划提供理论基础。

本文所提方法解决了传统方法中未充分考虑用户出行意愿及充电站选择导致充电负荷时空分布预测不准的问题。但本文算例模型中路网规模较小，尚未考虑天气类型和电价对EV 用户出行特性的影响。在后续研究中，将围绕多区域大规模路网、配电网下，计及天气类型和电价影响的EV 充电负荷时空分布开展研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。